Sorting algorithms

Prof. Sonu Gupta
Sorting
 Internal sort
 All data held in primary memory during sorting.
 External sort
 Uses primary memory for data currently being sorted &
secondary storage for any data that will not fit in memory.

Prof. Sonu Gupta
Sorting Concepts
 Sort order
 Sequence of sorted data – ascending/descending.
 Sort stability
 How data with equal keys maintain their relative input
order in output.
 In-place sort
 Manipulates elements to be sorted within the array or list
space that contained original unsorted input.
 Pass
 One full trip through the array comparing and if
necessary, swapping elements.

Prof. Sonu Gupta
Bubble Sort
 Process
 Compare each adjacent pair of items in a list
 Swap the items if not in order
 Repeat the pass through the list until no swaps are done.

Prof. Sonu Gupta
0
10
20
30
40
50
60
70
[1] [2] [3] [4] [5] [6]
0
10
20
30
40
50
60
70
[1] [2] [3] [4] [5] [6]
Swap?
0
10
20
30
40
50
60
70
[1] [2] [3] [4] [5] [6]
Yes!
0
10
20
30
40
50
60
70
[1] [2] [3] [4] [5] [6]
Swap?

Prof. Sonu Gupta
0
10
20
30
40
50
60
70
[1] [2] [3] [4] [5] [6]Swap?
0
10
20
30
40
50
60
70
[1] [2] [3] [4] [5] [6]
Swap?
0
10
20
30
40
50
60
70
[1] [2] [3] [4] [5] [6]
Yes! 0
10
20
30
40
50
60
70
[1] [2] [3] [4] [5] [6]
Swap?

Prof. Sonu GuptaProcess Continues…….
0
10
20
30
40
50
60
70
[1] [2] [3] [4] [5] [6]
Yes!
I pass gets over….now
repeat again
0
10
20
30
40
50
60
70
[1] [2] [3] [4] [5] [6]
Swap?
0
10
20
30
40
50
60
70
[1] [2] [3] [4] [5] [6]
Swap?
Yes

Prof. Sonu Gupta
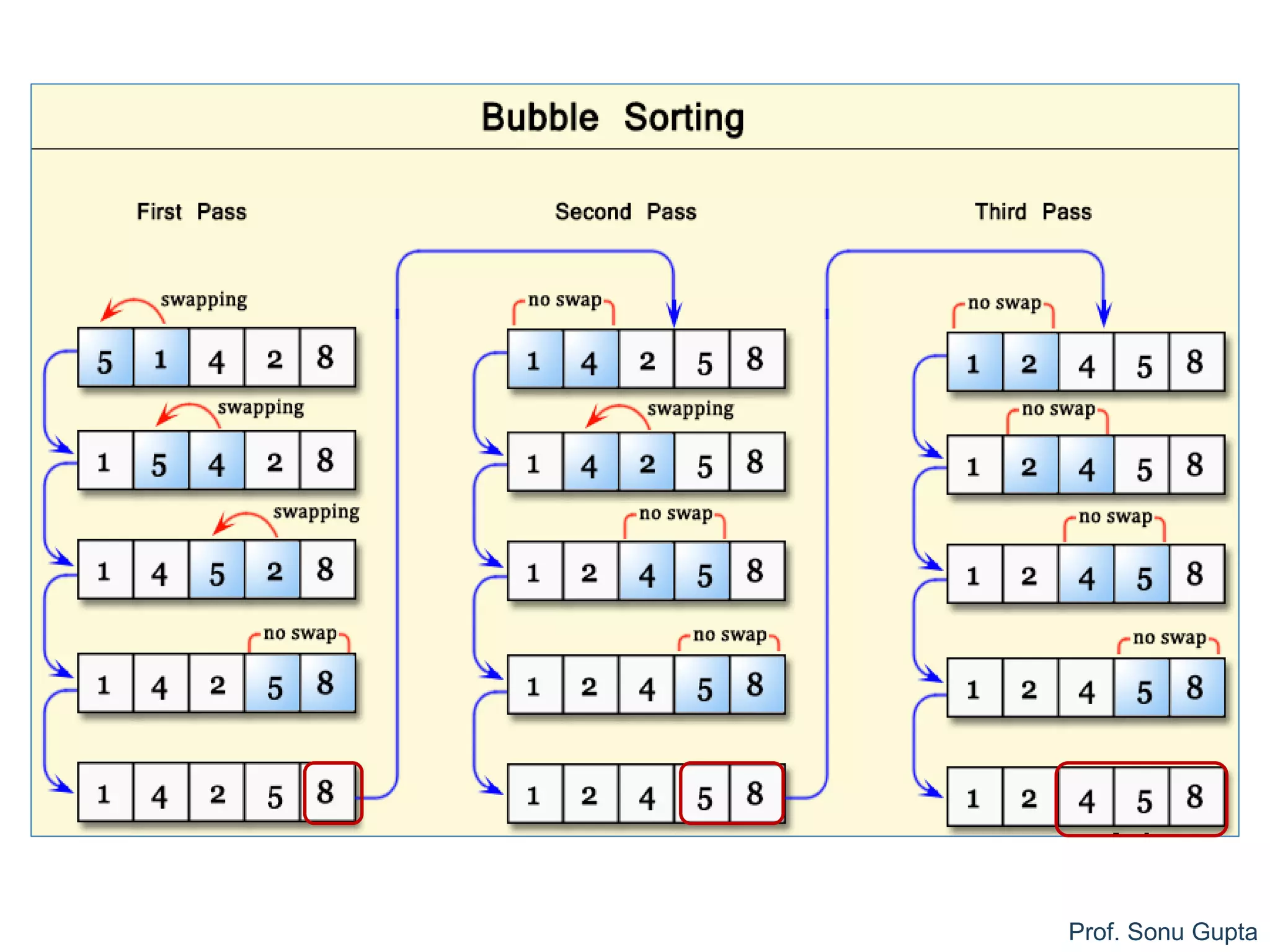
Bubble Sort
Algorithm bubble (a, n)
Pre: Unsorted array ‘a’ of length ‘n’.
Post: Sorted array in ascending order of length n
1. for i = 1 to (n - 1) do //n-1 passes
1. for j = 0 to n - 2 do //n-1 comparison in every pass
1. if ( a[j] > a[j+1] ) //out of order
1. temp=a[j]
2. a[j]=a[j+1]
3. a[j+1]=temp

Prof. Sonu Gupta
Optimizations in Bubble Sort
 Stop further passes if no data exchanged i.e. list is
now sorted
 Do not compare elements placed at their proper
position in every pass (sorted part of array)
………..
………..
Unsorted Array Sorted Array

Prof. Sonu Gupta
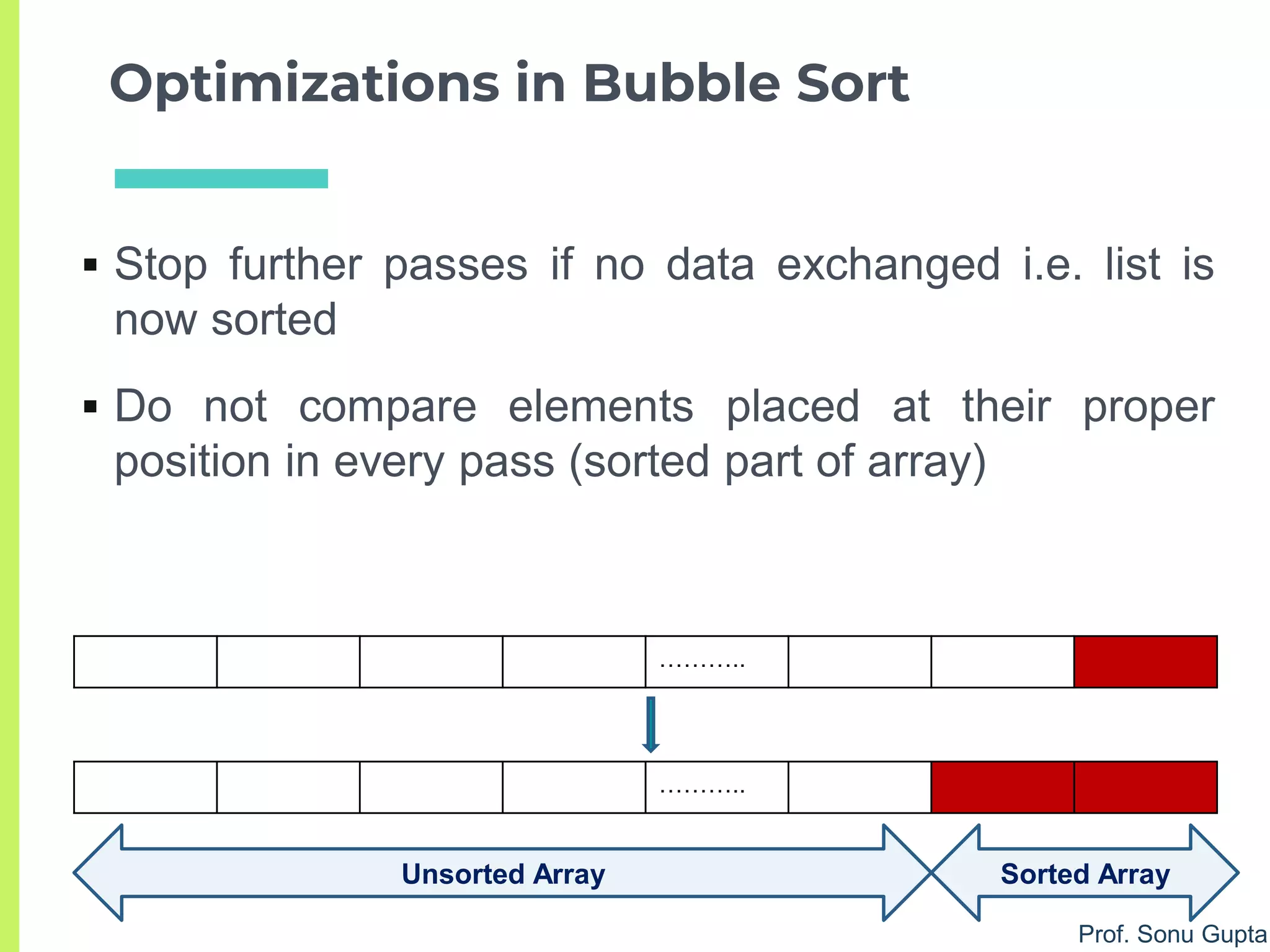
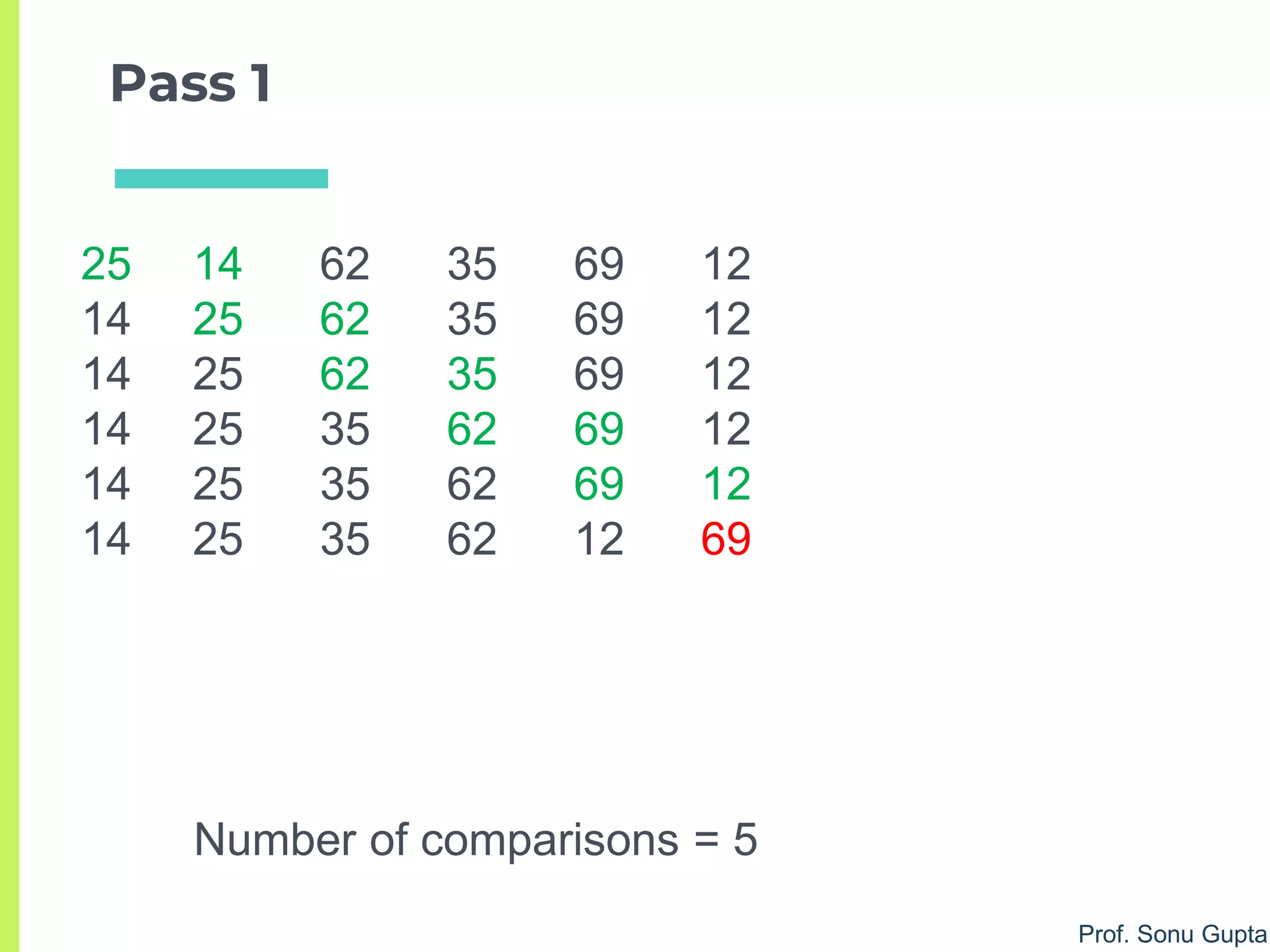
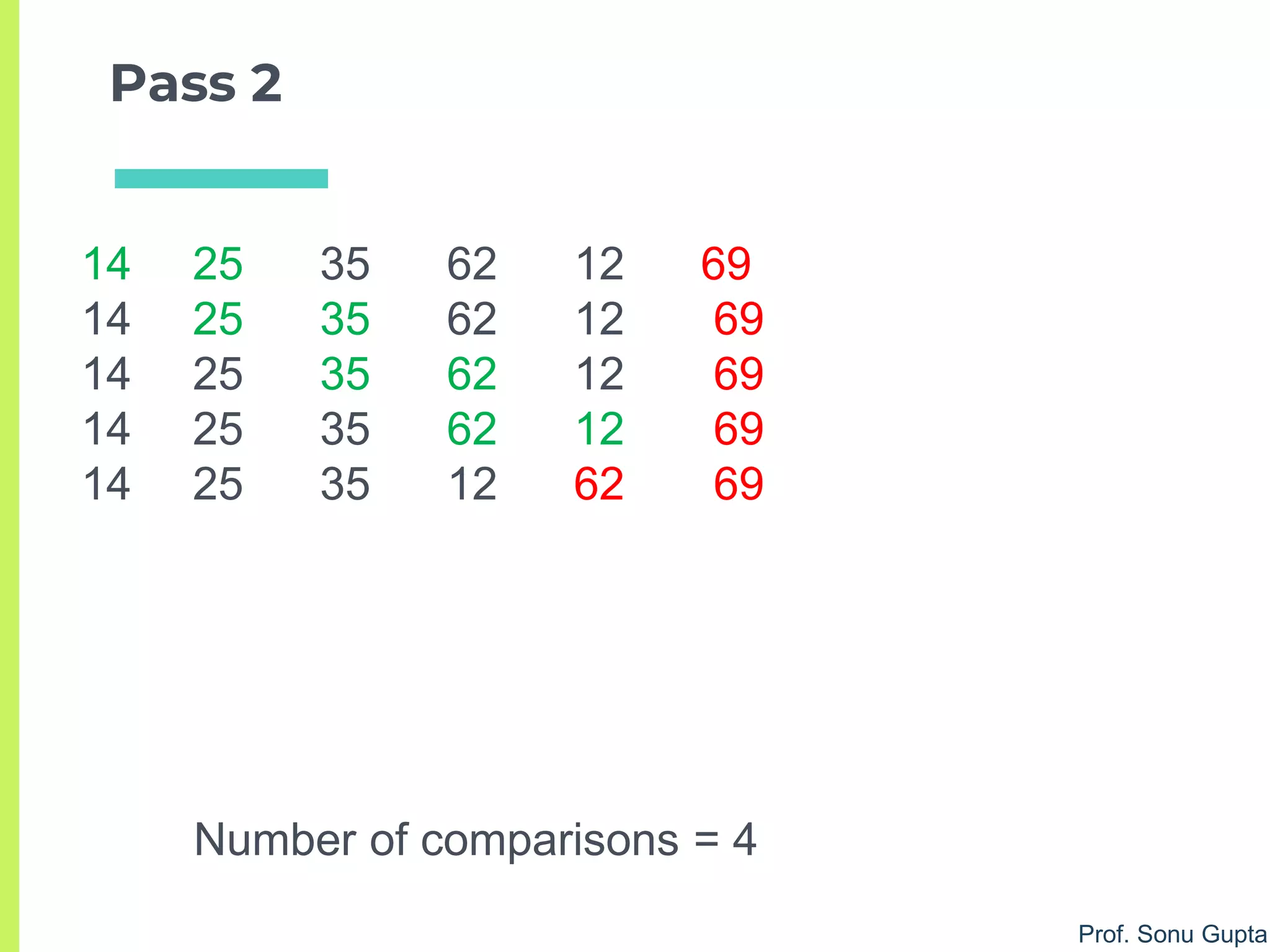
Bubble Sort - Optimized
Algorithm bubble (a, n)
Post: Sorted array in ascending order of length n
1. for i = 1 to (n – 1) do // n-1 passes
1. test = 0
2. for j = 0 to ((n-1) – i ) do //don’t compare sorted data
1. if ( a[j] > a[j+1] )
1. temp=a[j]
2. a[j]=a[j+1]
3. a[j+1]=temp
4. test = 1 / / exchange happened
3. if (test = 0) // no exchange - list is now sorted
1. return

Prof. Sonu Gupta
Complexity
 Worst Case: - O (n2)
Number of comparison in 1st pass : n-1
Number of comparison in 2nd pass : n-2
…..
Number of comparison in last pass : 1
Total number of comparison:
(n-1)+(n-2)+……+1
=n(n-1)/2 // Using sum of natural numbers
=(n2-n)/2 = O(n2)
 Best Case: - O (n)
List already sorted, 1 pass of n-1 comparisons.

Prof. Sonu Gupta
Exercise
 Sort the following numbers using bubble sort.
25 14 62 35 69 12

Prof. Sonu Gupta
Pass 1
25 14 62 35 69 12
14 25 62 35 69 12
14 25 62 35 69 12
14 25 35 62 69 12
14 25 35 62 69 12
14 25 35 62 12 69
Number of comparisons = 5

Prof. Sonu Gupta
Pass 2
14 25 35 62 12 69
14 25 35 62 12 69
14 25 35 62 12 69
14 25 35 62 12 69
14 25 35 12 62 69

Prof. Sonu Gupta
Pass 3
14 25 35 12 62 69
14 25 35 12 62 69
14 25 35 12 62 69
14 25 12 35 62 69

Prof. Sonu Gupta
Pass 4
14 25 12 35 62 69
14 25 12 35 62 69
14 12 25 35 62 69

Prof. Sonu Gupta
Pass 5
14 12 25 35 62 69
12 14 25 35 62 69

Prof. Sonu Gupta
Exercise
 Sort following elements using bubble sort method.
7 8 10 26 44 33

Prof. Sonu Gupta
Pass 1
7 8 10 26 44 33
7 8 10 26 44 33
7 8 10 26 44 33
7 8 10 26 44 33
7 8 10 26 44 33
7 8 10 26 33 44
Exchange of numbers occurred =1

Prof. Sonu Gupta
Pass 2
7 8 10 26 33 44
7 8 10 26 33 44
7 8 10 26 33 44
7 8 10 26 33 44
7 8 10 26 33 44
No exchange of numbers
Hence skip further pass.

Prof. Sonu Gupta
Selection Sort
 During each pass, the smallest (or largest) value is moved
to its proper position in the array.
 Process
 Find & place smallest value at 1st place
 Find & place 2nd smallest value at 2nd place
 ……….

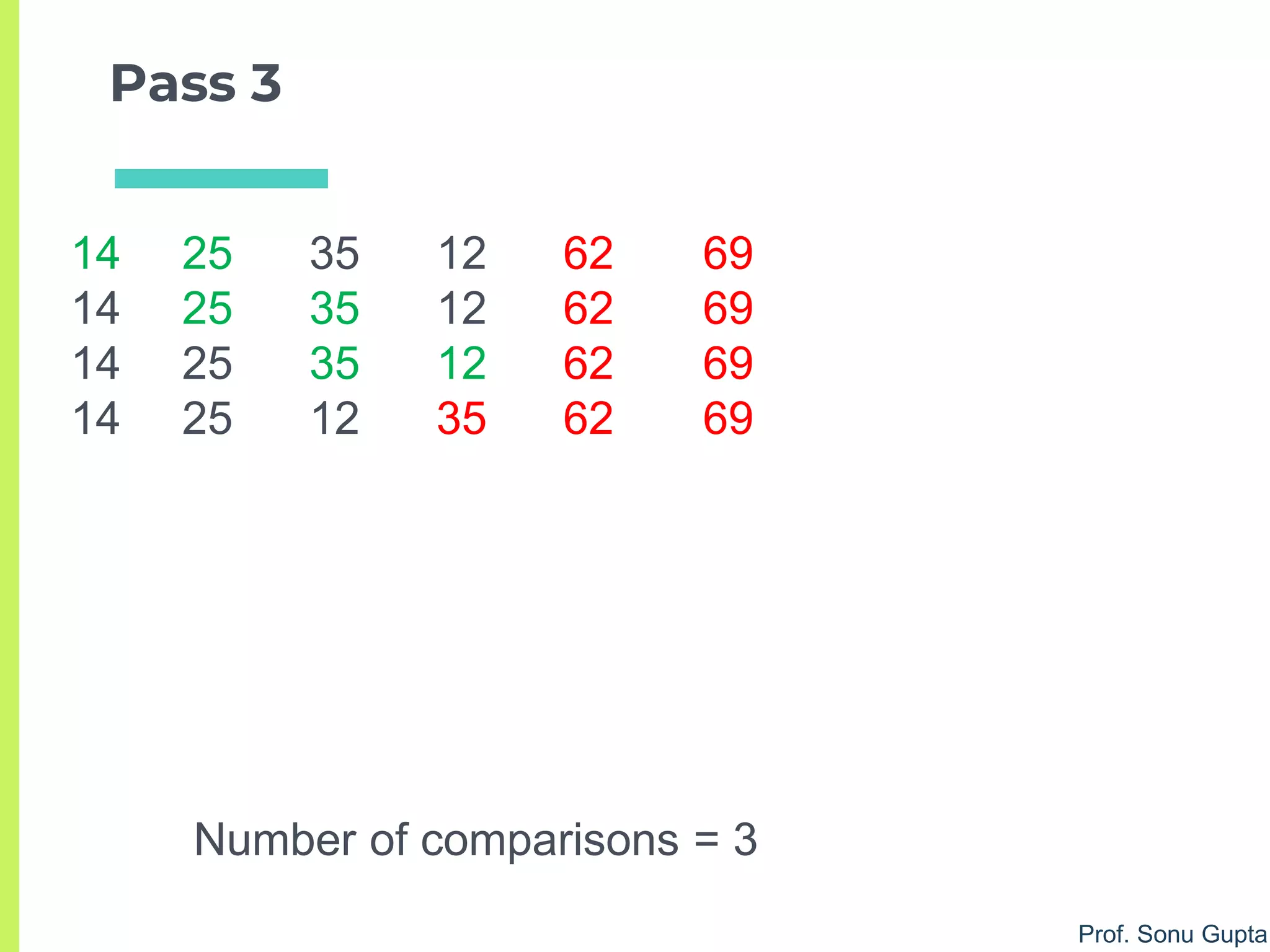
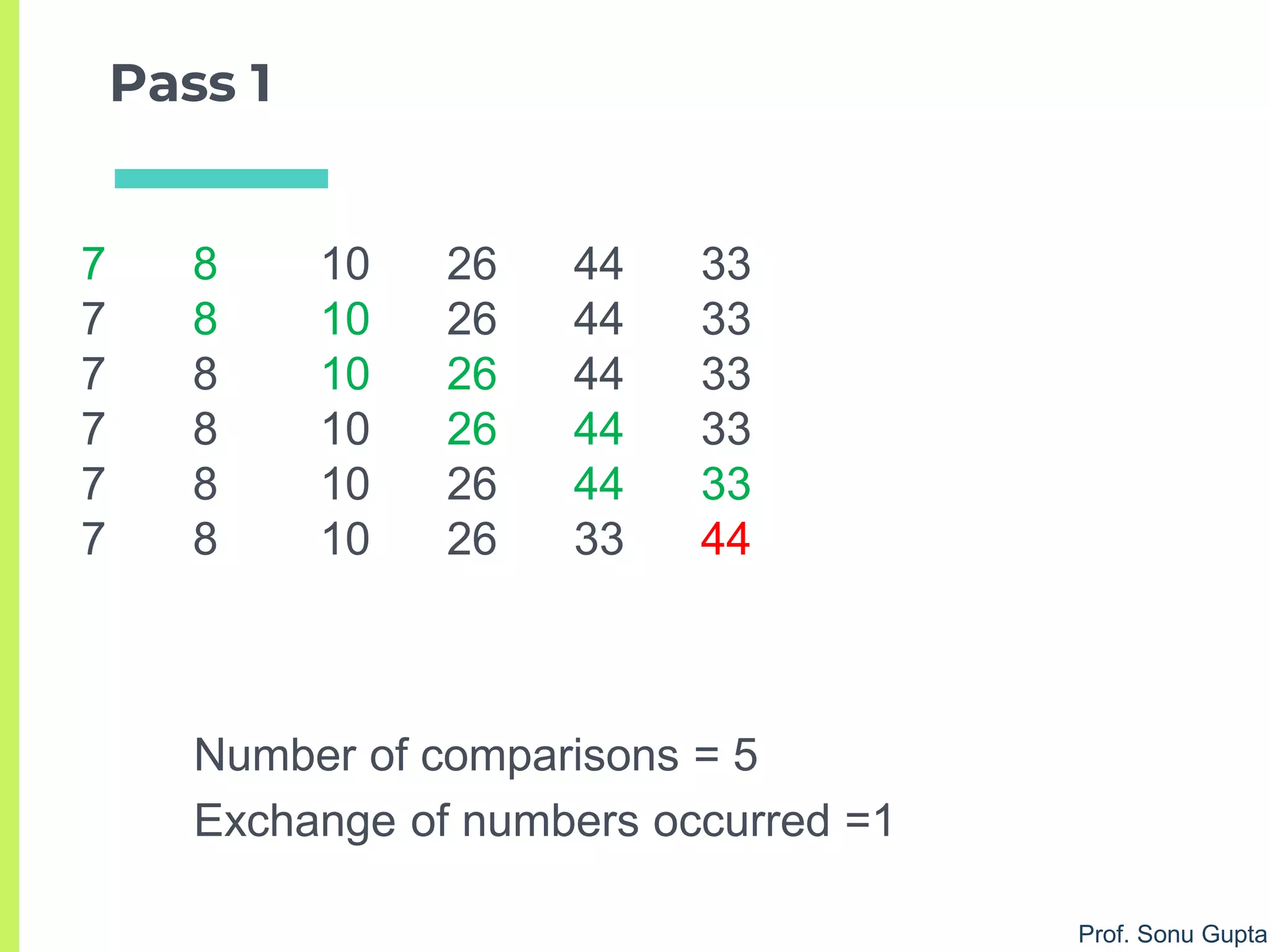
Prof. Sonu Gupta
0
10
20
30
40
50
60
70
[1] [2] [3] [4] [5] [6]
0
10
20
30
40
50
60
70
[1] [2] [3] [4] [5] [6]
0
10
20
30
40
50
60
70
[1] [2] [3] [4] [5] [6]
0
10
20
30
40
50
60
70
[1] [2] [3] [4] [5] [6]
I pass gets over
0
10
20
30
40
50
60
70
[1] [2] [3] [4] [5] [6]
0
10
20
30
40
50
60
70
[1] [2] [3] [4] [5] [6]
Sorted side Unsorted side

Prof. Sonu Gupta
0
10
20
30
40
50
60
70
[1] [2] [3] [4] [5] [6]
0
10
20
30
40
50
60
70
[1] [2] [3] [4] [5] [6]
0
10
20
30
40
50
60
70
[1] [2] [3] [4] [5] [6]
0
10
20
30
40
50
60
70
[1] [2] [3] [4] [5] [6]
0
10
20
30
40
50
60
70
[1] [2] [3] [4] [5] [6]
0
10
20
30
40
50
60
70
[1] [2] [3] [4] [5] [6]
Smallest
from
unsorted
0
10
20
30
40
50
60
70
[1] [2] [3] [4] [5] [6]
0
10
20
30
40
50
60
70
[1] [2] [3] [4] [5] [6]

Prof. Sonu Gupta
0
10
20
30
40
50
60
70
[1] [2] [3] [4] [5] [6]
0
10
20
30
40
50
60
70
[1] [2] [3] [4] [5] [6]
Process Continues…….

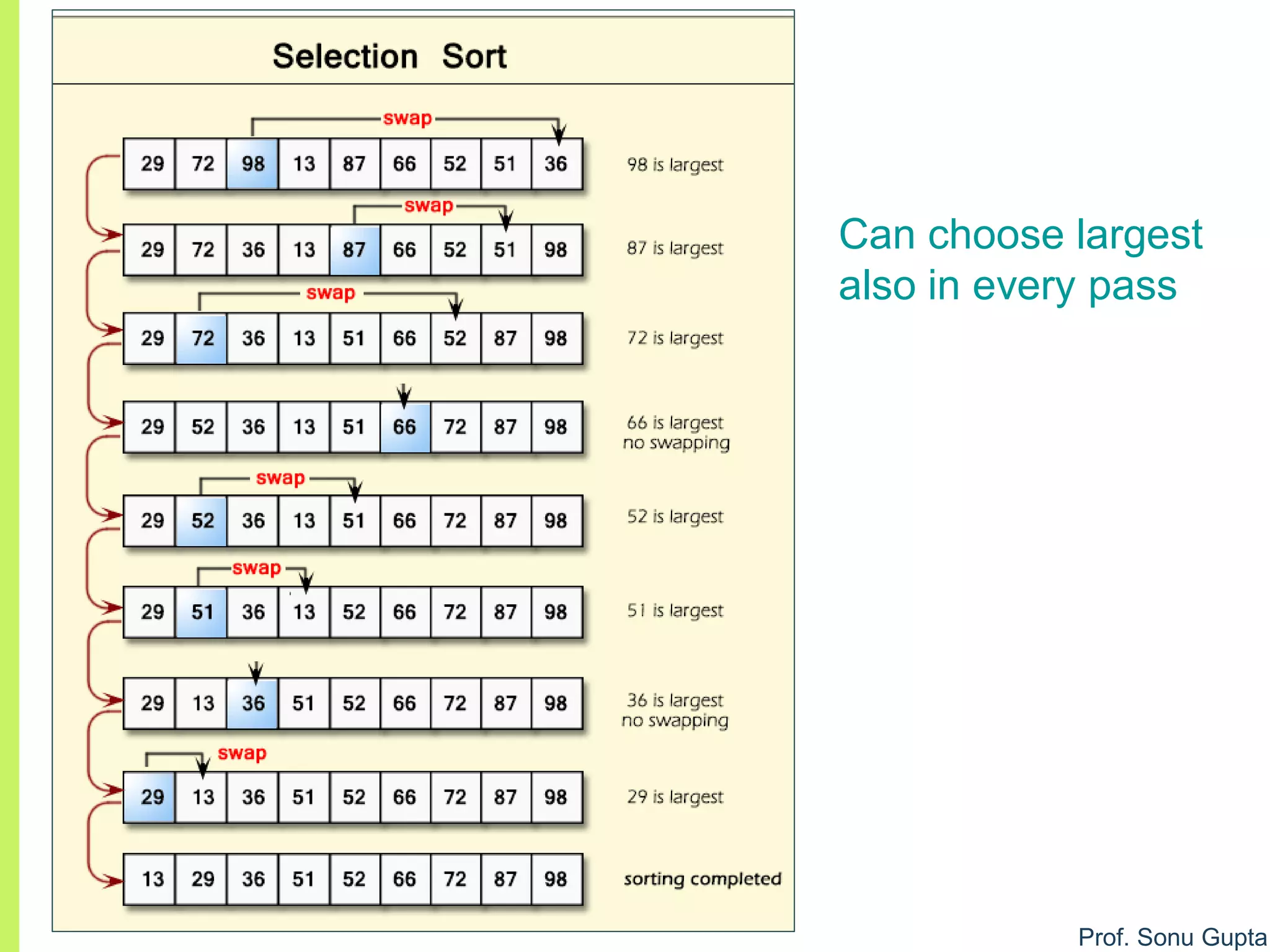
Prof. Sonu Gupta
Can choose largest
also in every pass

Prof. Sonu Gupta
Selection Sort
Algorithm selection (a, length)
Post: Sorted list in ascending order of length n
1. for i = 0 to (n -2) do // n-1 passes
1. min_index=i
2. for j = (i+1) to (n -1) do
1. if ( a[min_index] > a[j] )
1. min_index = j
3. if (min_index < > i) // place ith smallest element at ith place
1. temp= a[i]
2. a[i]=a[min_index]
3. a[min_index]=temp

Prof. Sonu Gupta
Complexity
 Worst & Best Case: - O (n2)
I pass (n-1) comparisons, II pass (n-2) comparisons & so
on.
Thus, total comparisons-
(n-1) + (n-2) + (n-3) + …. + (1)
= ( n(n-1))/2 // Using sum of natural numbers
= O(n2)
(Worst & best cases are same as an element has to be
compared to all others to ensure that it is minimum.)

Prof. Sonu Gupta
Insertion Sort
 Sort by repeatedly taking the next item and inserting it into
the final data structure in its proper order with respect to
items already inserted.
 Process
 Assume 1st element to be sorted
 Insert 2nd element in correct position with respect to 1st
 Insert 3rd element in correct position with respect to 1st &
2nd
 Repeat till array sorted

Prof. Sonu Gupta
0
10
20
30
40
50
60
70
[1] [2] [3] [4] [5] [6]
0
10
20
30
40
50
60
70
[1] [2] [3] [4] [5] [6]
0
10
20
30
40
50
60
70
[1] [2] [3] [4] [5] [6]
0
10
20
30
40
50
60
70
[1] [2] [3] [4] [5] [6]
0
10
20
30
40
50
60
70
[1] [2] [3] [4] [5] [6]
0
10
20
30
40
50
60
70
[1] [2] [3] [4] [5] [6]

Prof. Sonu Gupta
0
10
20
30
40
50
60
70
[1] [2] [3] [4] [5] [6]
0
10
20
30
40
50
60
70
[1] [2] [3] [4] [5] [6]
0
10
20
30
40
50
60
70
[1] [2] [3] [4] [5] [6]
0
10
20
30
40
50
60
70
[1] [2] [3] [4] [5] [6]
0
10
20
30
40
50
60
70
[1] [2] [3] [4] [5] [6]
0
10
20
30
40
50
60
70
[1] [2] [3] [4] [5] [6]
First pass gets over

Prof. Sonu Gupta
Process Continues…….
0
10
20
30
40
50
60
70
[1] [2] [3] [4] [5] [6]
0
10
20
30
40
50
60
70
[1] [2] [3] [4] [5] [6]
0
10
20
30
40
50
60
70
[1] [2] [3] [4] [5] [6]
0
10
20
30
40
50
60
70
[1] [2] [3] [4] [5] [6]

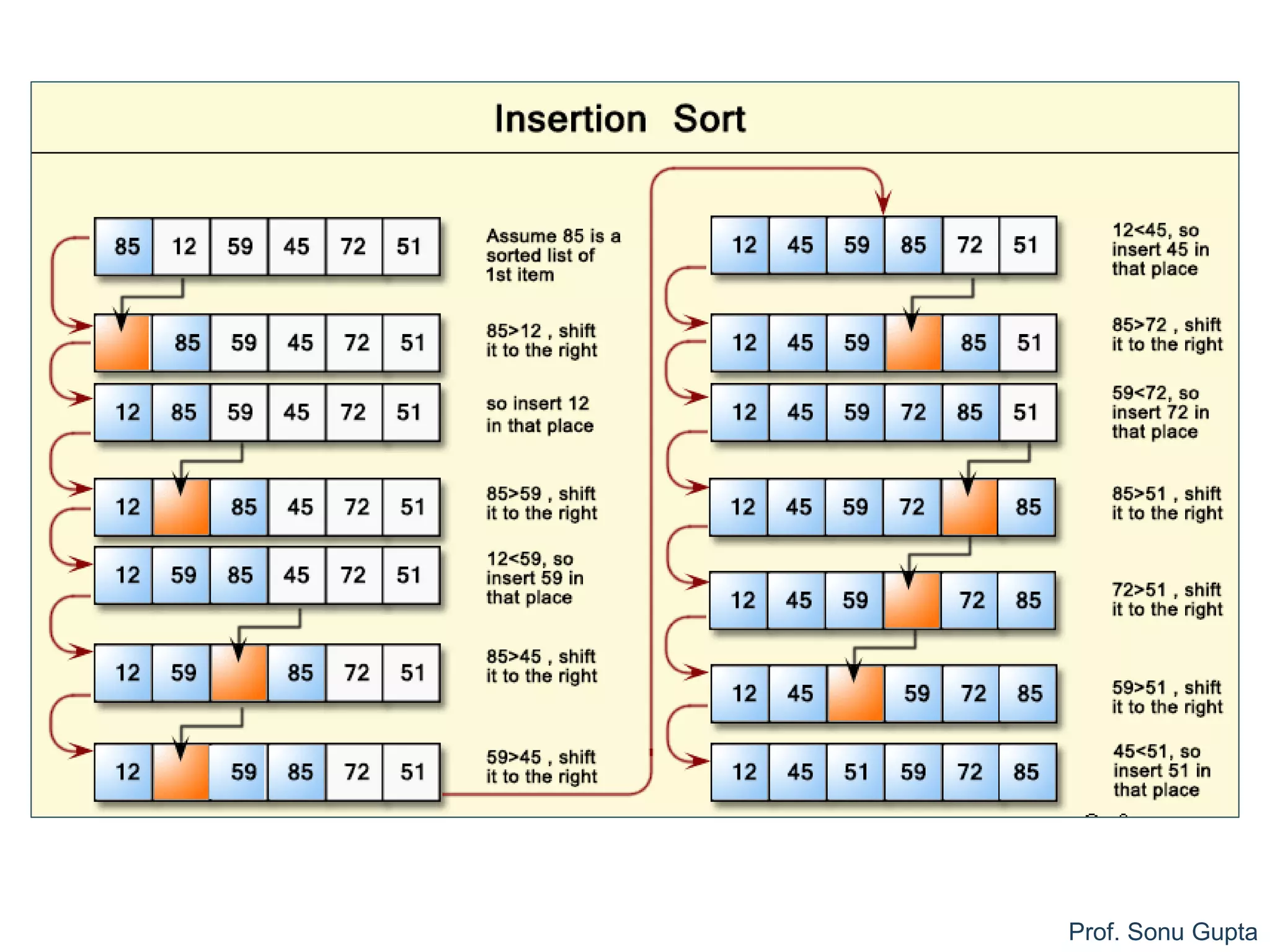
Prof. Sonu Gupta
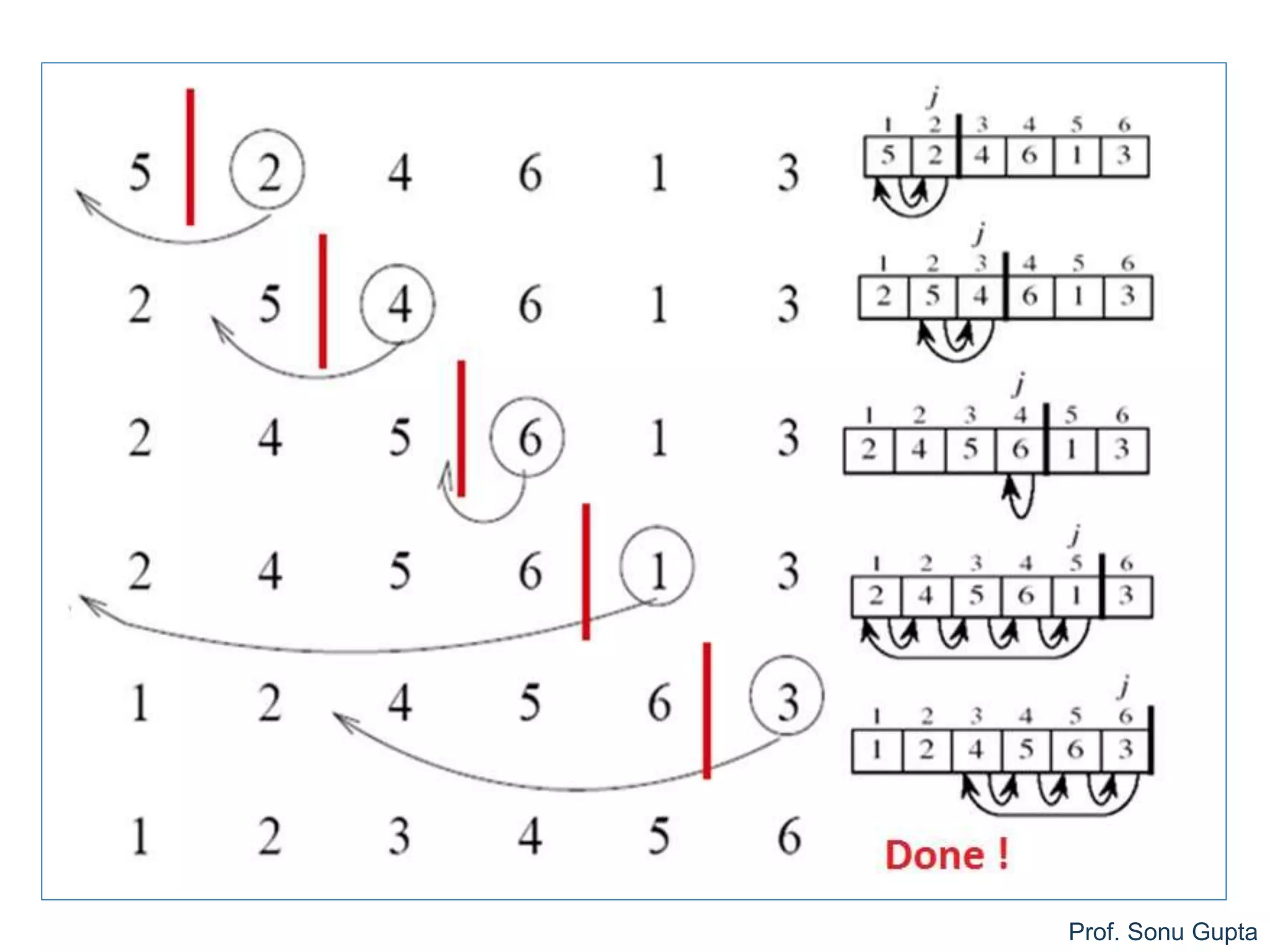
Insertion Sort
Algorithm insertion (a, length)
Pre: Unsorted list ‘a’ of length ‘n’.
Post: Sorted list a in ascending order of length n
1. for i = 1 to (n -1) do // n-1 passes
1. indata=a[i]
2. for j = (i-1) downto 0 do
1. if ( indata < a[j] )
1. a[j+1] = a[j] // shift elements
2. else
1. break
2. a[j+1] = indata // insert element at proper position

Prof. Sonu Gupta
Complexity
 Best Case: - O (n)
List is already sorted. In each iteration, first element of
unsorted list compared with last element of sorted list, thus
(n-1) comparisons.
 Worst Case: - O(n2)
List sorted in reverse order. First element of unsorted list
compared with one element of sorted list, second
compared with 2 elements. Last element to be inserted
compared with all the n-1 elements.
1 + 2 + 3 + ………………… (n-2) + (n-1)
= (n (n-1))/2
= O (n2)
 Average Case: - O(n2)

Prof. Sonu Gupta
 Sort
5 2 4 6 1 3

Prof. Sonu Gupta
Shell Sort
 Diminishing increment sort
 In each pass, each element is compared with the element
that is located ‘d’ indexes away from it, and an exchange
is made if required.
 d is preferably prime
 The next pass starts with a new value of d. In each pass,
the value of d is reduced to half.
 The algorithm terminates when d=1. Works as insertion
sort.
 Complexity: O (n1.25) (calculated empirically)

Prof. Sonu Gupta
Example
Original file
25 57 48 37 12 92 86 33
Pass 1: span 5
25 57 48 37 12 92 86 33
25 57 33 37 12 92 86 48

Prof. Sonu Gupta
Example
25 57 33 37 12 92 86 48
Pass 2: span 3
25 57 33 37 12 92 86 48
25 12 33 37 48 92 86 57

Prof. Sonu Gupta
Example
25 12 33 37 48 92 86 57
Pass 3: span 1 (now insertion sort)
25 12 33 37 48 92 86 57
12 25 33 37 48 57 86 92

Prof. Sonu Gupta
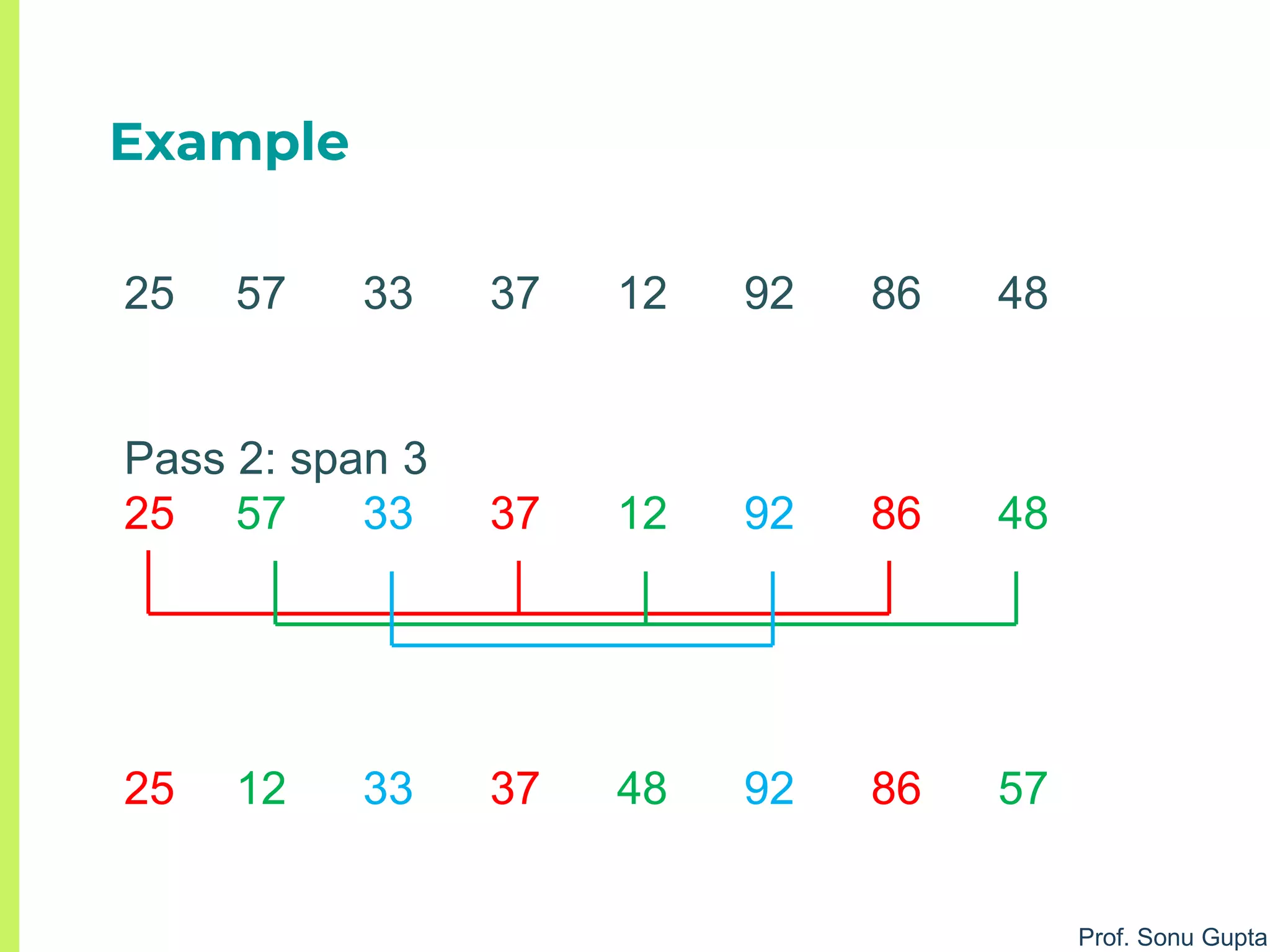
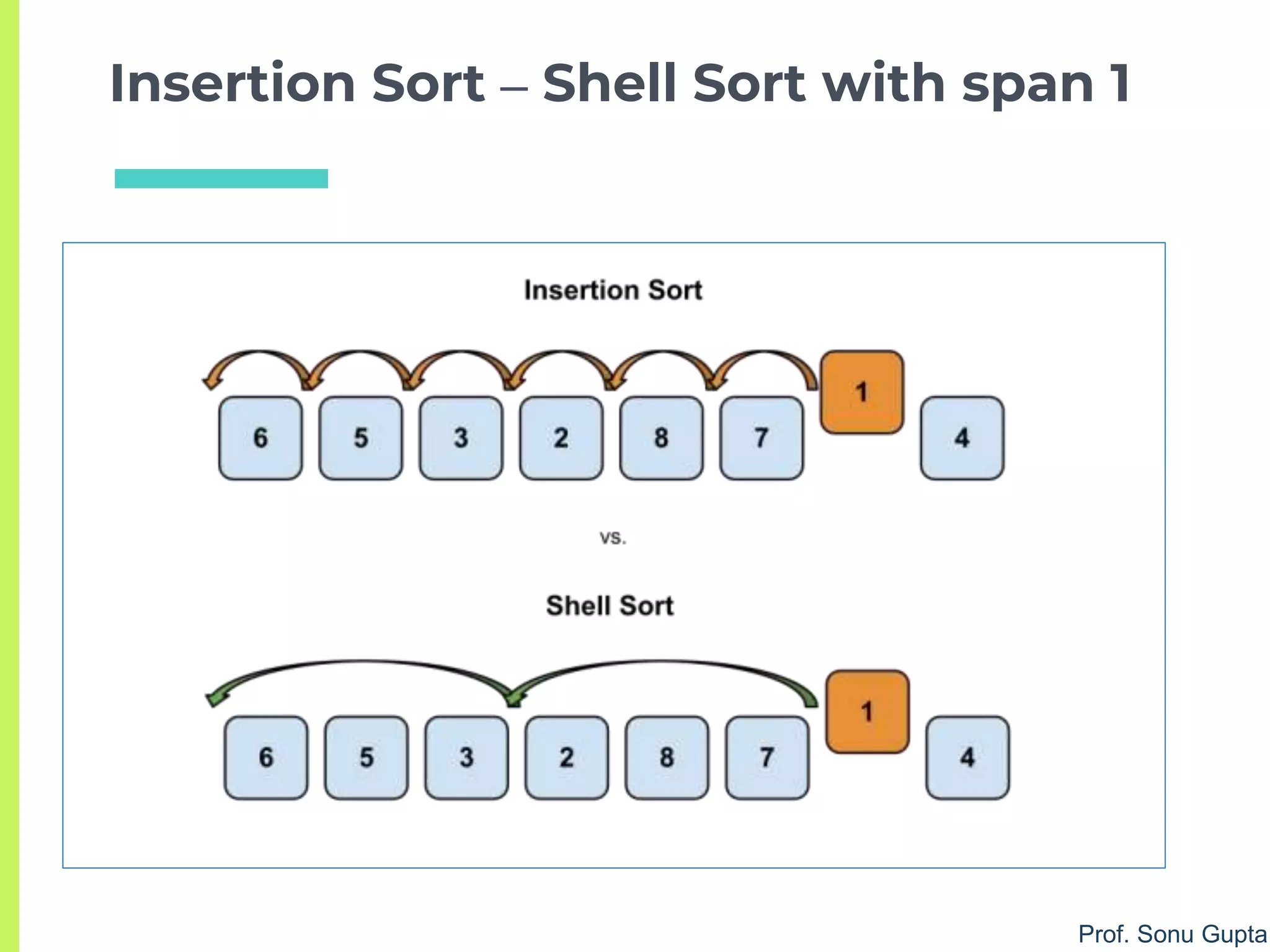
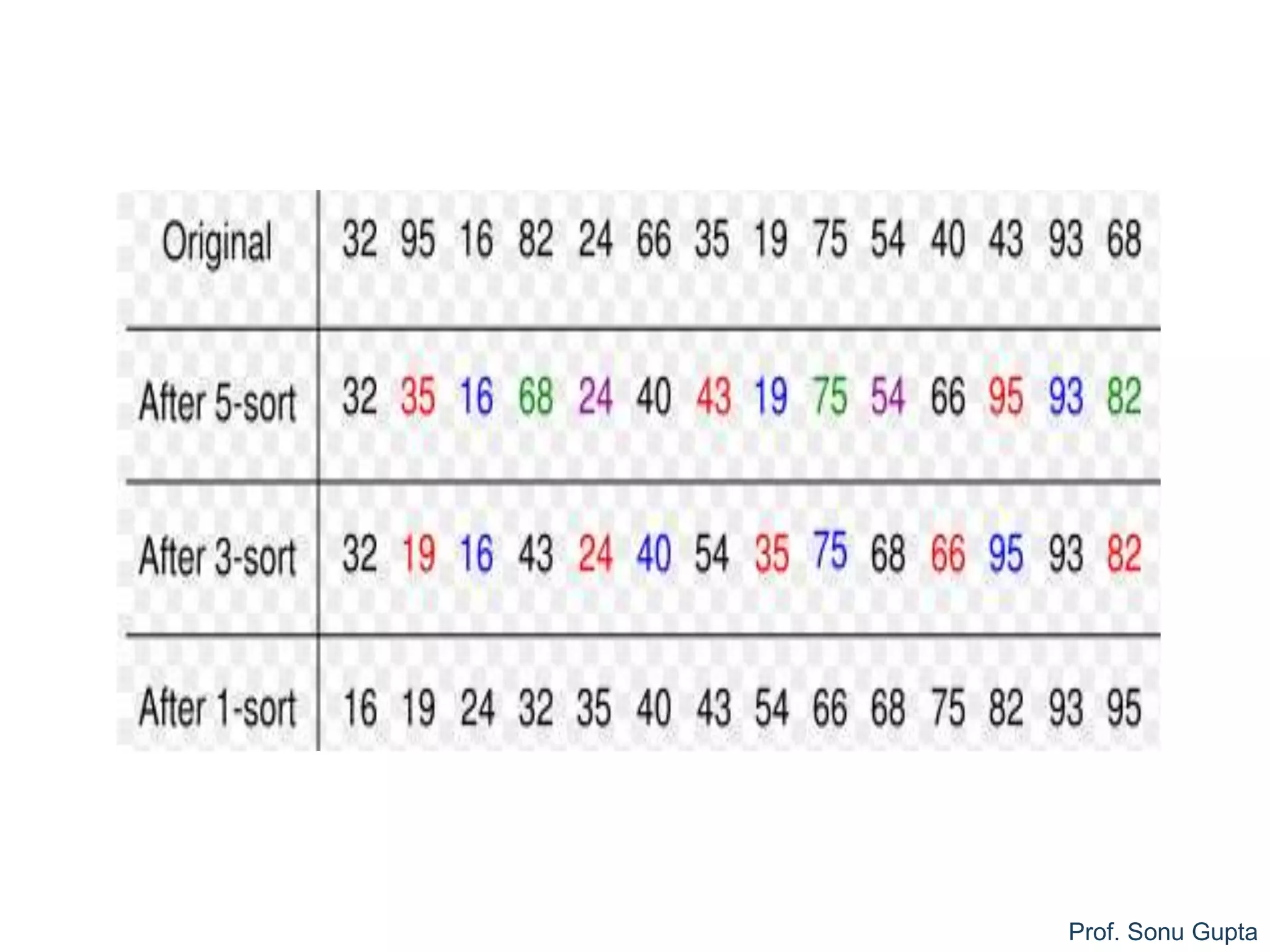
Shell Sort
Algorithm shell (a, n, inc, n_inc)
// unsorted array a, n – array size, inc – array of diminishing
increment values, n_inc - size of array increments
Pre: Unsorted list of length n.
1. for increment = 0 to (n_inc - 1) do
1. span = inc[increment] //choose increment
2. for j = span to (n-1) do //pass
1. y = a[j]
2. for k = (j-span) downto 0 step span
1. if (y < a[k])
1. a[k + span]=a[k]
2. else
1. break
3. a[k + span] = y

Prof. Sonu Gupta
Insertion Sort – Shell Sort with span 1

Prof. Sonu Gupta
Quick sort
 Quicksort sorts by employing a divide and conquer
strategy to divide a list into two sub-lists.
 The steps are:
 Pick an element, called a pivot, from the list.
 Partition operation - Reorder the list so that all elements
which are less than the pivot come before the pivot and
all elements greater than the pivot come after it (equal
values can go either way). After this partitioning, the pivot
is in its final position.
 Recursively sort the sub-list of lesser elements and the
sub-list of greater elements.

Prof. Sonu Gupta
57 92 48 37 86 12 70 89
57
37 12 48 86 92 70 89
57
37
12 48
86
70 89 92
Quick Sort

Prof. Sonu Gupta
57
37
12 48
86
70 89
92
COMBINE
12 37 48 57 70 86 89 92

Prof. Sonu Gupta
Algorithm quicksort (a, beg, end)
// a - array to be sorted, beg - starting index of array to be
sorted, end - ending index of array to be sorted
Pre: Unsorted list a of length n.
1. if (beg < end)
1. pivot = partition(a, beg, end)
2. quicksort(a, beg, pivot-1) // recursively sort left & right array
3. quicksort (a, pivot+1, end)

Prof. Sonu Gupta
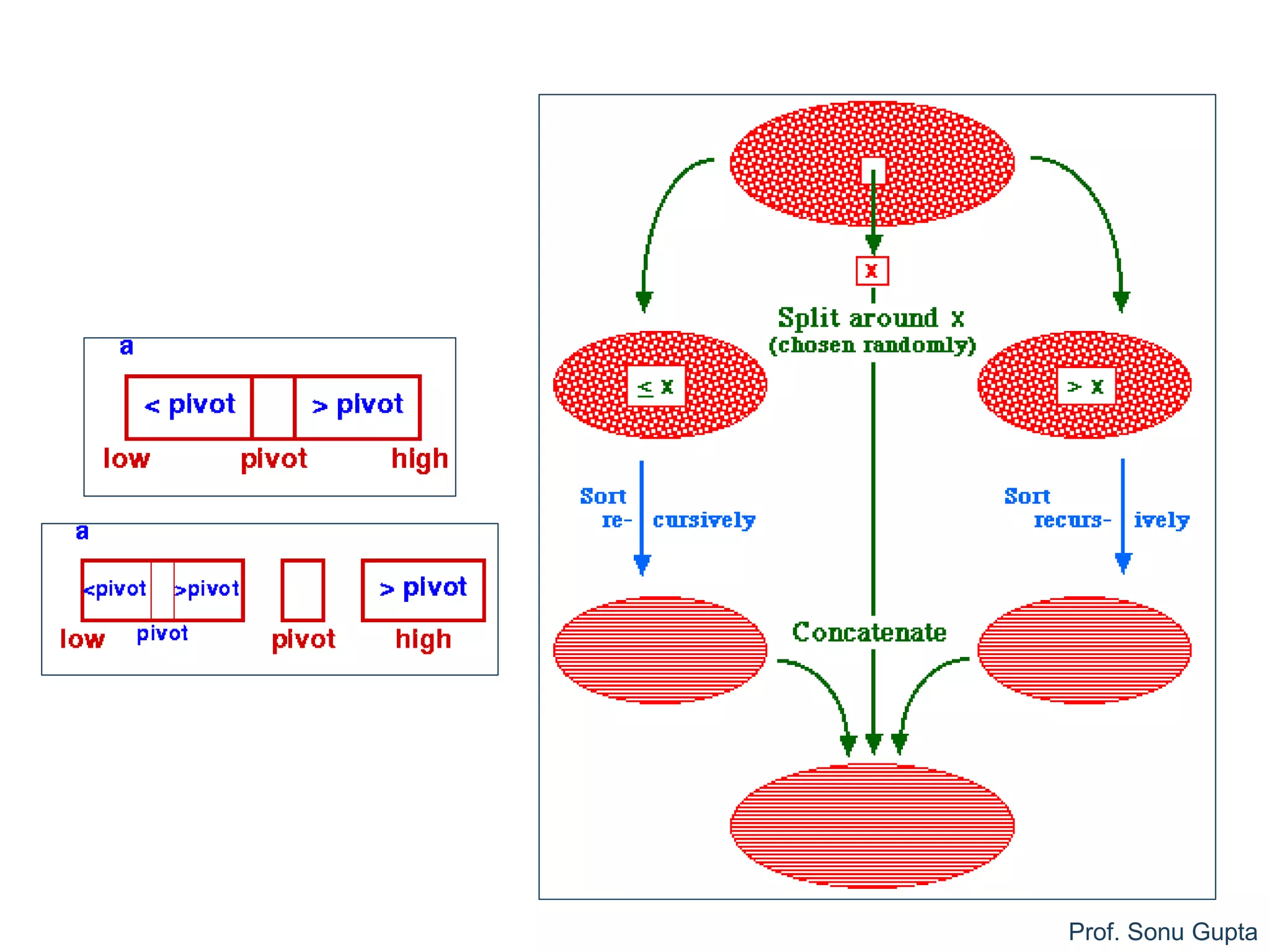
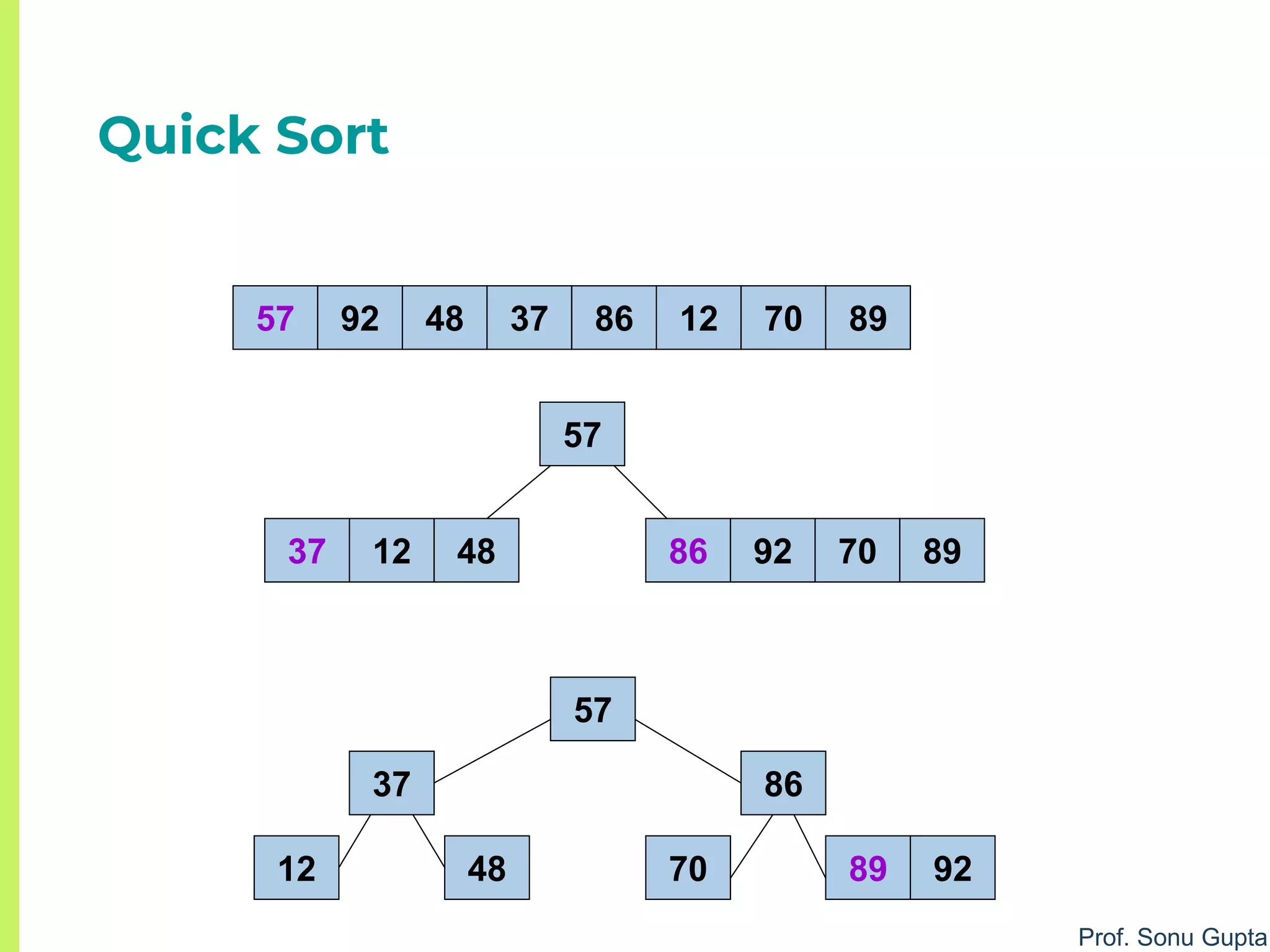
partition (a, beg, end)
// Places pivot element piv at its proper position; elements
before it are less than it & after it are greater than it
1. piv = a[beg]
2. up = end
3. down = beg
4. while (down < up)
1.while( (a[down] <= piv) & (down < up))
1.down=down + 1
2.while(a[up]>piv)
1.up=up-1
3.if (down<up)
1.swap ( a[down], a[up])
5. swap(a[beg],a[up])
6. return up

Prof. Sonu Gupta
Quick sort Partition Example
81 94 11 96 12 35 17 95 28 58 41 75 15
D U
81 15 11 96 12 35 17 95 28 58 41 75 94
D U
81 15 11 75 12 35 17 95 28 58 41 96 94
D U
Swap
81 15 11 75 12 35 17 41 28 58 95 96 94
D U
81 15 11 75 12 35 17 41 28 58 95 96 94
U D
Down>Up
58 15 11 75 12 35 17 41 28 81 95 96 94
81 94 11 96 12 35 17 95 28 58 41 75 15
D U
Swap
Swap

Prof. Sonu Gupta
 Sort array
65, 21, 14, 97, 87, 78, 74, 76, 45, 84, 22

Prof. Sonu Gupta
Best Case Partitioning
Median of the array is chosen as the pivot value at every stage.

Prof. Sonu Gupta
Worst Case Partitioning
Each time the pivot selected is the smallest/largest value in
array

Prof. Sonu Gupta
Complexity
 Best Case: O (n log n)
Assume n = 2m, m = log2n.
1st pass file split in two parts each of size n/2
2nd pass 4 parts of size n/4,
3rd pass 8 parts of size n/8
After m pass, there will be n files each of size 1
Total no. of comparisons:-
= (2 * n/2) + (4*n/4) + (8 * n/8)+………(m*n/m)
=n+n+n………………..m times
=n*m = O (n log n)

Prof. Sonu Gupta
Complexity
 Worst Case : O (n2)
If file already sorted than partition of size 0 & n-1& so on.
T(n)=partition(n) + T(n-1)
=n+T(n-1)
=n+partition(n-1) + T(n-2)
=n+(n-1)+T(n-2)
=n+(n-1)+(n-2)+…………1
=n(n+1)/2
= O(n2)

Prof. Sonu Gupta
Merge Sort
 Divide and conquer strategy
 The steps are –
 Divide the unsorted list into two sub lists of about half
the size.
 Sort each sub list recursively by re-applying merge
sort, till you reach a single element array
 Merge the sub lists back into one sorted list.

Prof. Sonu Gupta
Merging
two lists

Prof. Sonu Gupta
Merge Sort
Algorithm mergesort (a, low, high)
// a is array to be sorted, low is starting index of array to be
sorted, high is ending index of array to be sorted
Pre: Unsorted list of length n.
1. if (low < high)
1. mid = (low + high)/2
2. mergesort(x, low, mid)
3. mergesort(x, (mid+1), high)
4. merge(x, low, mid, high)

Prof. Sonu Gupta
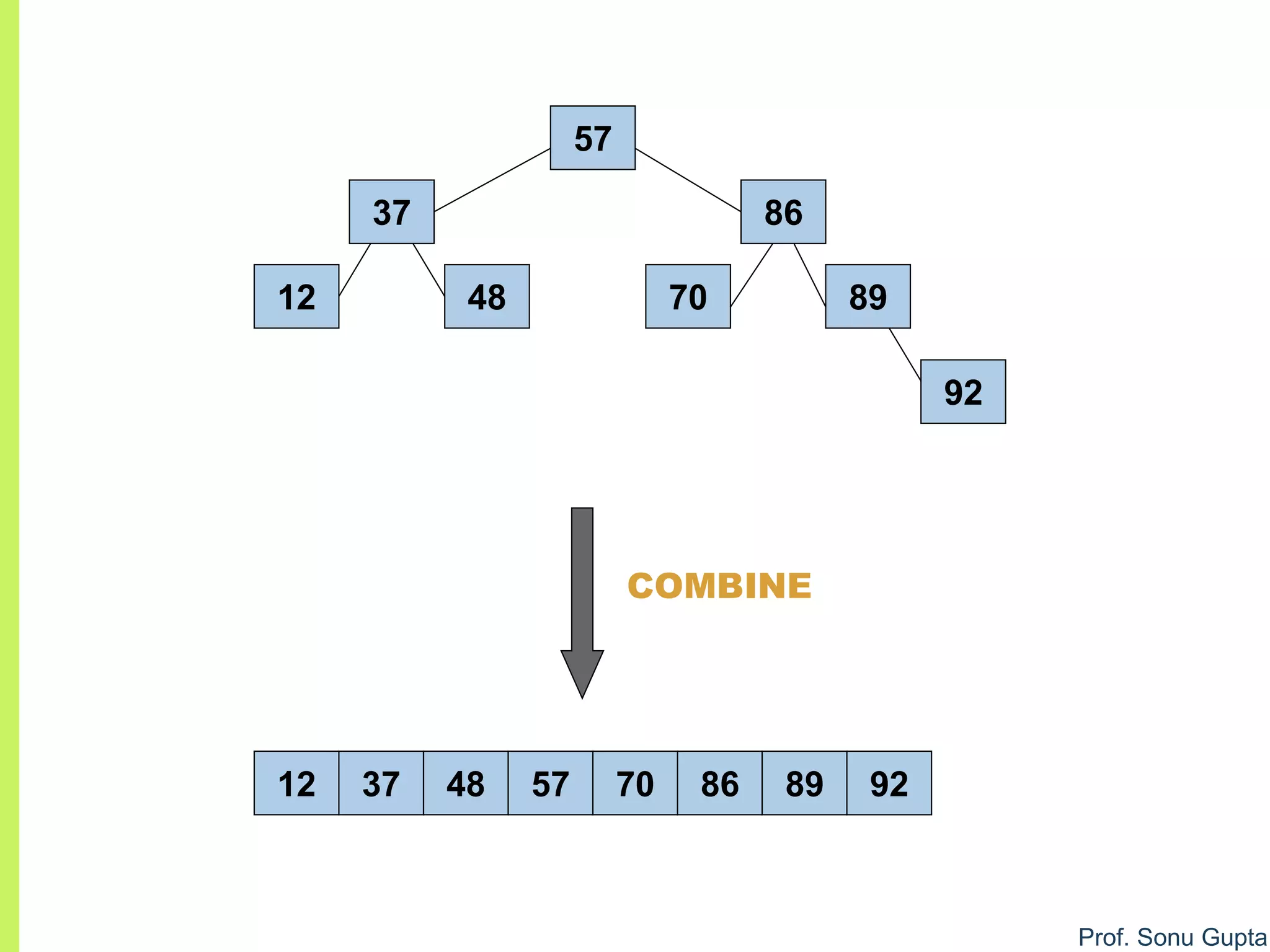
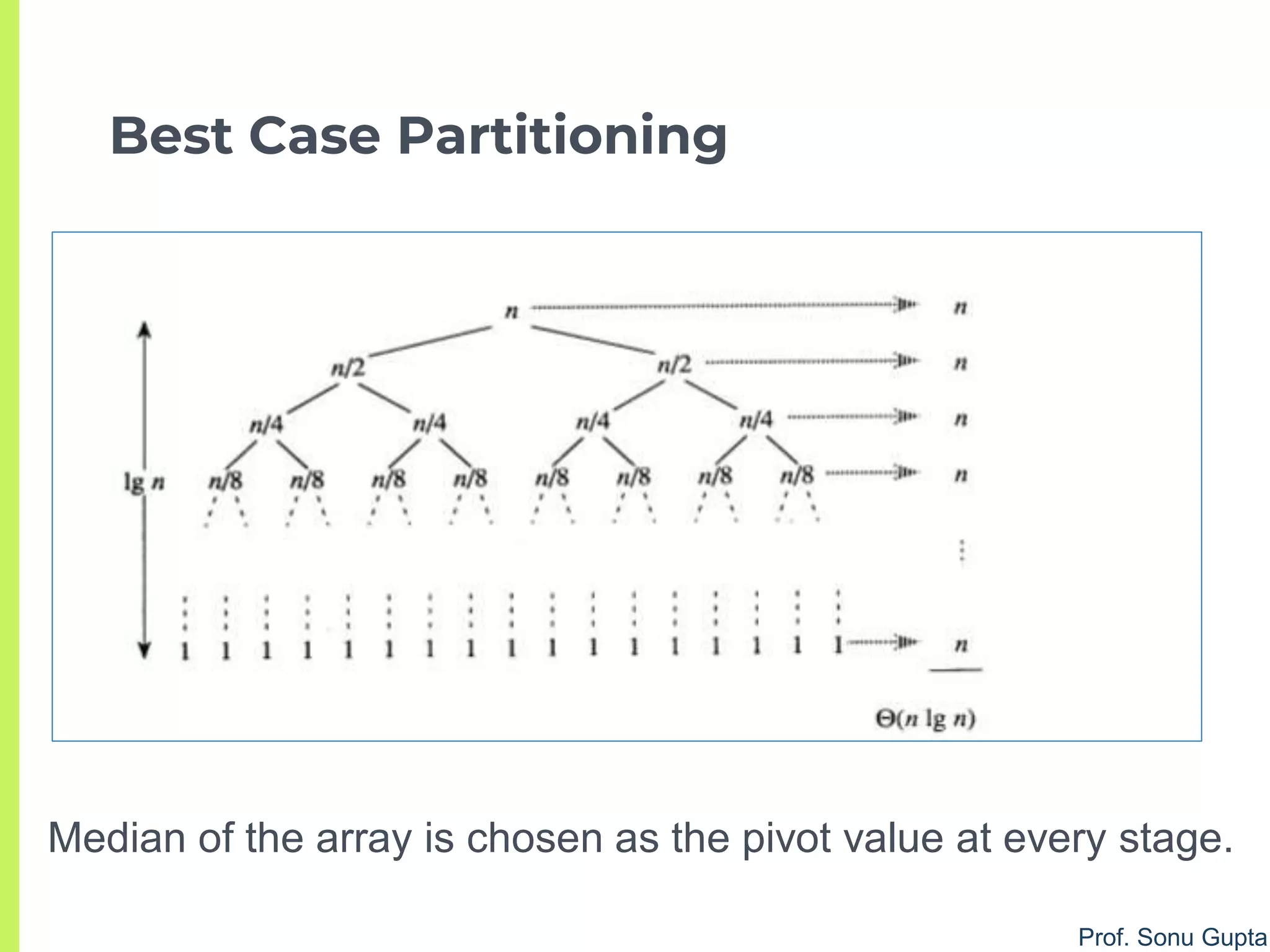
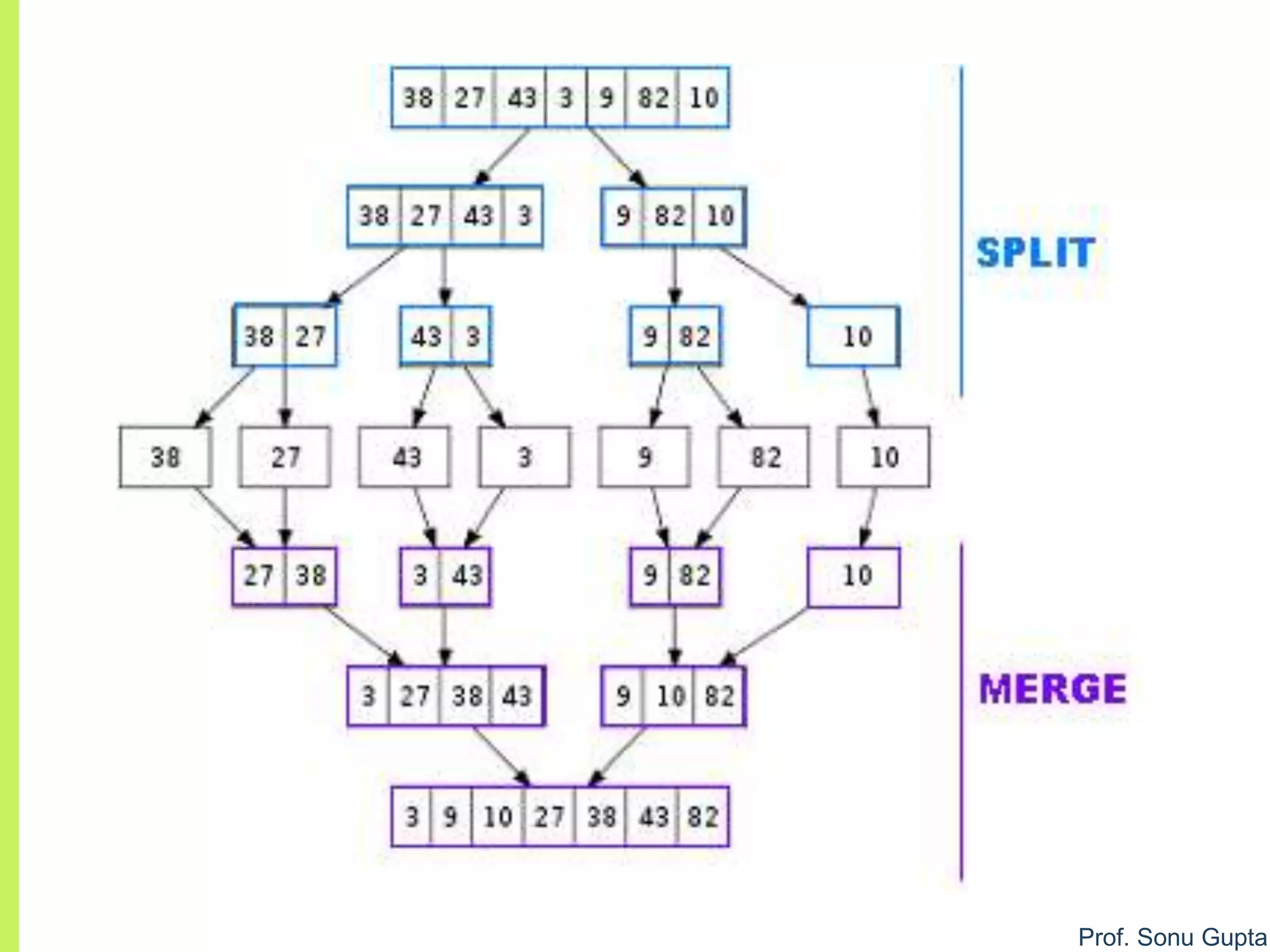
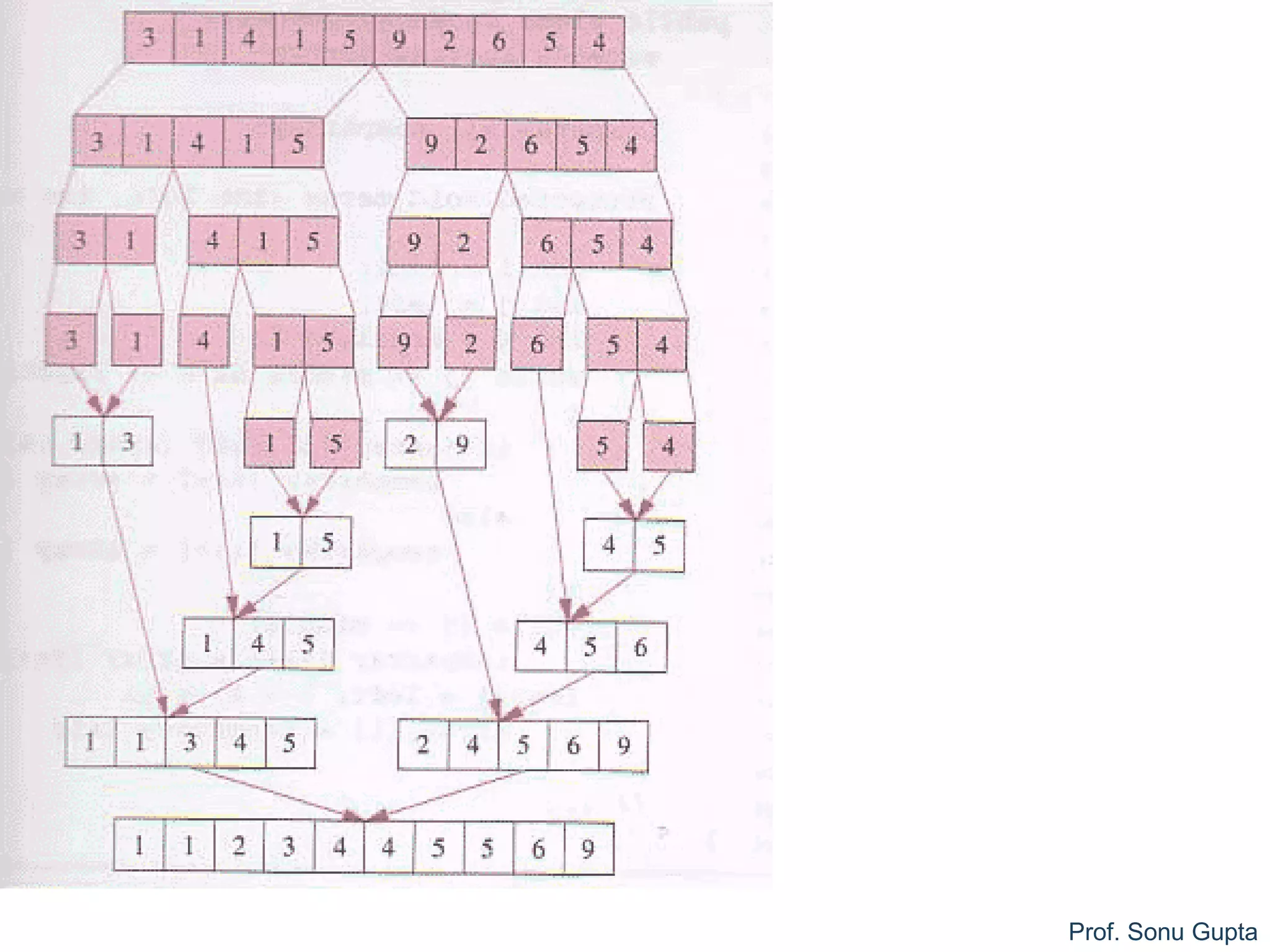
merge (a, low1, high1, high2)
1.i = low1; j = high1 + 1; k = 0
2.while (i<= high1) and (j<=high2) //Merge arrays
1. if (x[i] <=x[j])
1. aux[k] = x[i]
2. k=k+1; i=i+1
2. else
1. aux[k] = x[j]
2. k=k+1; j=j+1
3.while (i<= high1) // If jth list over, copy ith as it is
1. aux[k] = x[i]
2. k=k+1; i=i+1
4.while (j<= high2) // If ith list over, copy jth as it is
1. aux[k] = x[j]
2. k=k+1; j=j+1
5.k=0
6.for j = low1 to high2
1. a[j] = aux[k]
2. k = k+1

Prof. Sonu Gupta
Complexity
 Best Case, Average Case, Worst case: O (n log n)
Same as in quicksort
 Auxiliary Space: O(n)

Prof. Sonu Gupta
Radix Sort
 Radix sort is a stable lexicographic sorting algorithm that
sorts integers by processing individual digits.
 Uses bucket sort
 Two classifications of radix sorts
 Least significant digit process the integer representations
starting from the least significant digit and move towards
the most significant digit.
 Most significant digit process the integer representations
starting from the most significant digit and move towards
the least significant digit. This is also known as radix
exchange sort

Prof. Sonu Gupta
Radix Sort
 The steps in Least significant digit (LSD) radix sort
algorithm are as follows:
1. Take the least significant digit of each key.
2. Sort the list of elements based on that digit.
3. Repeat the sort with the immediate more significant
digit.

Prof. Sonu Gupta
Radix Sort - Pass 1
064 008 216 512 027 729 000 001 343 125
0
1
2
3
4
5
6
7
8
9
064
008
216
512
027
729
000
001
343
125
000 001 512 343 064 125 216 027 008 729

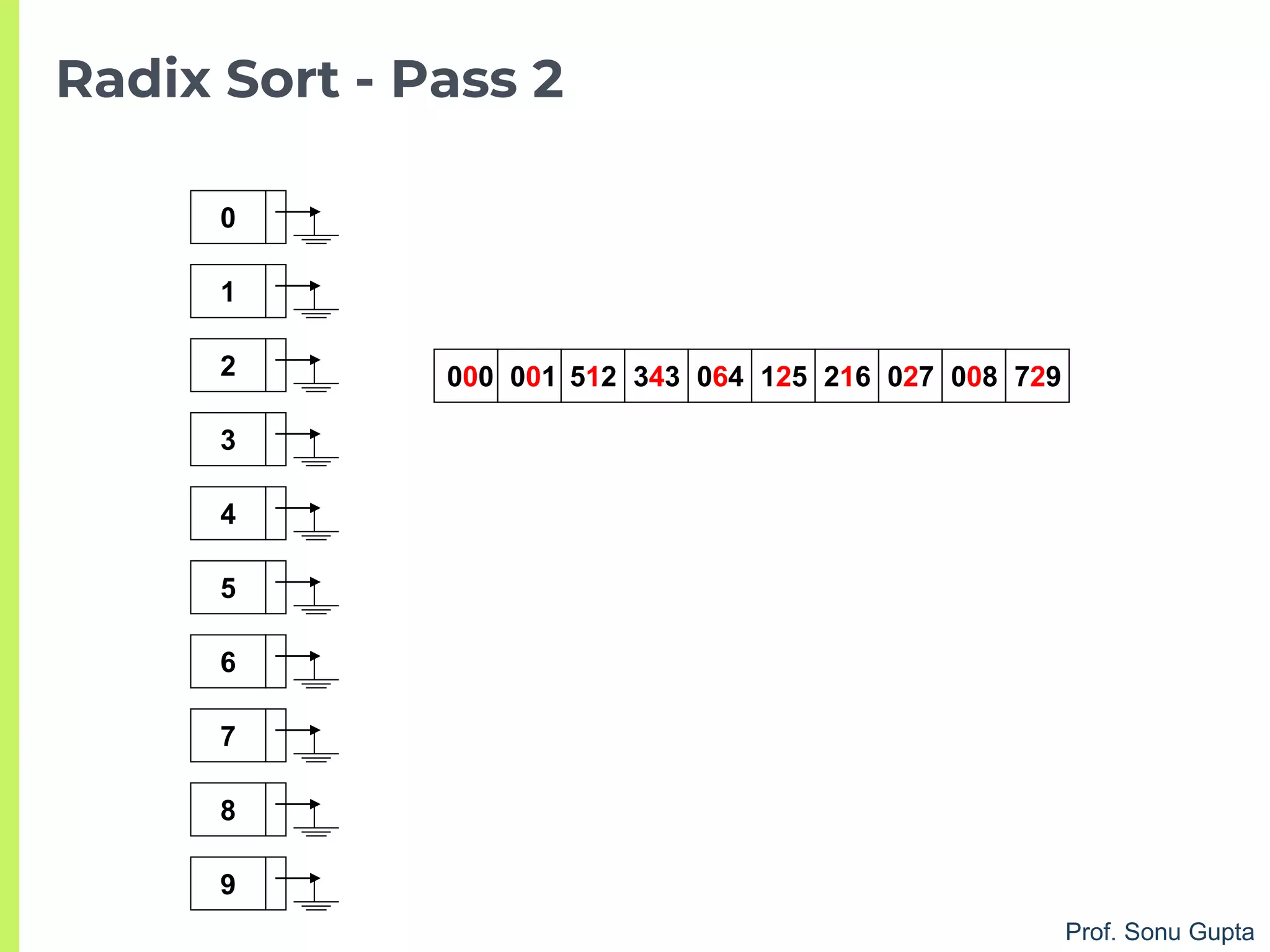
Prof. Sonu Gupta
000 001 512 343 064 125 216 027 008 729
0
1
2
3
4
5
6
7
8
9
Radix Sort - Pass 2

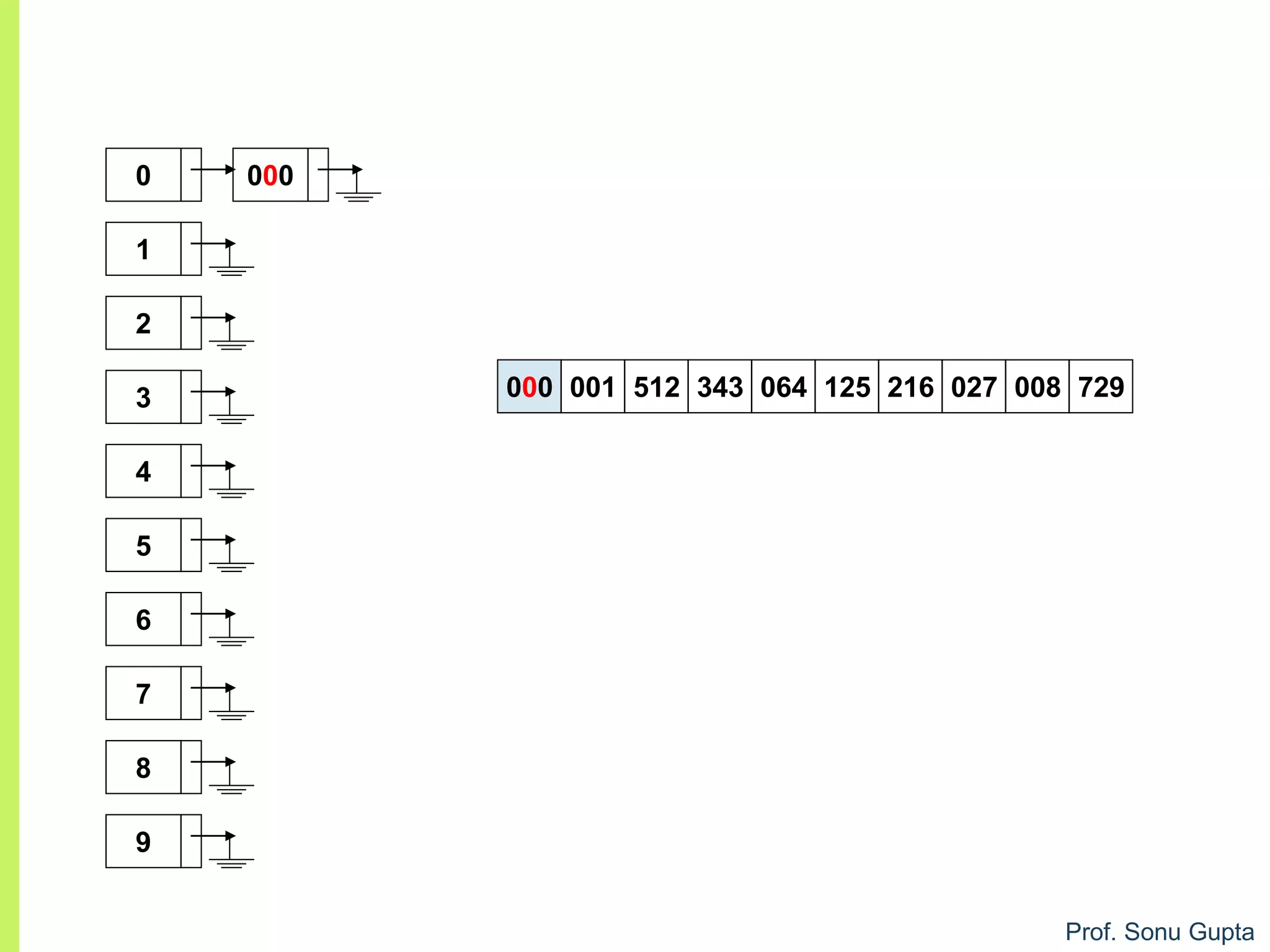
Prof. Sonu Gupta
000 001 512 343 064 125 216 027 008 729
1
2
3
4
5
6
7
8
9
0 000

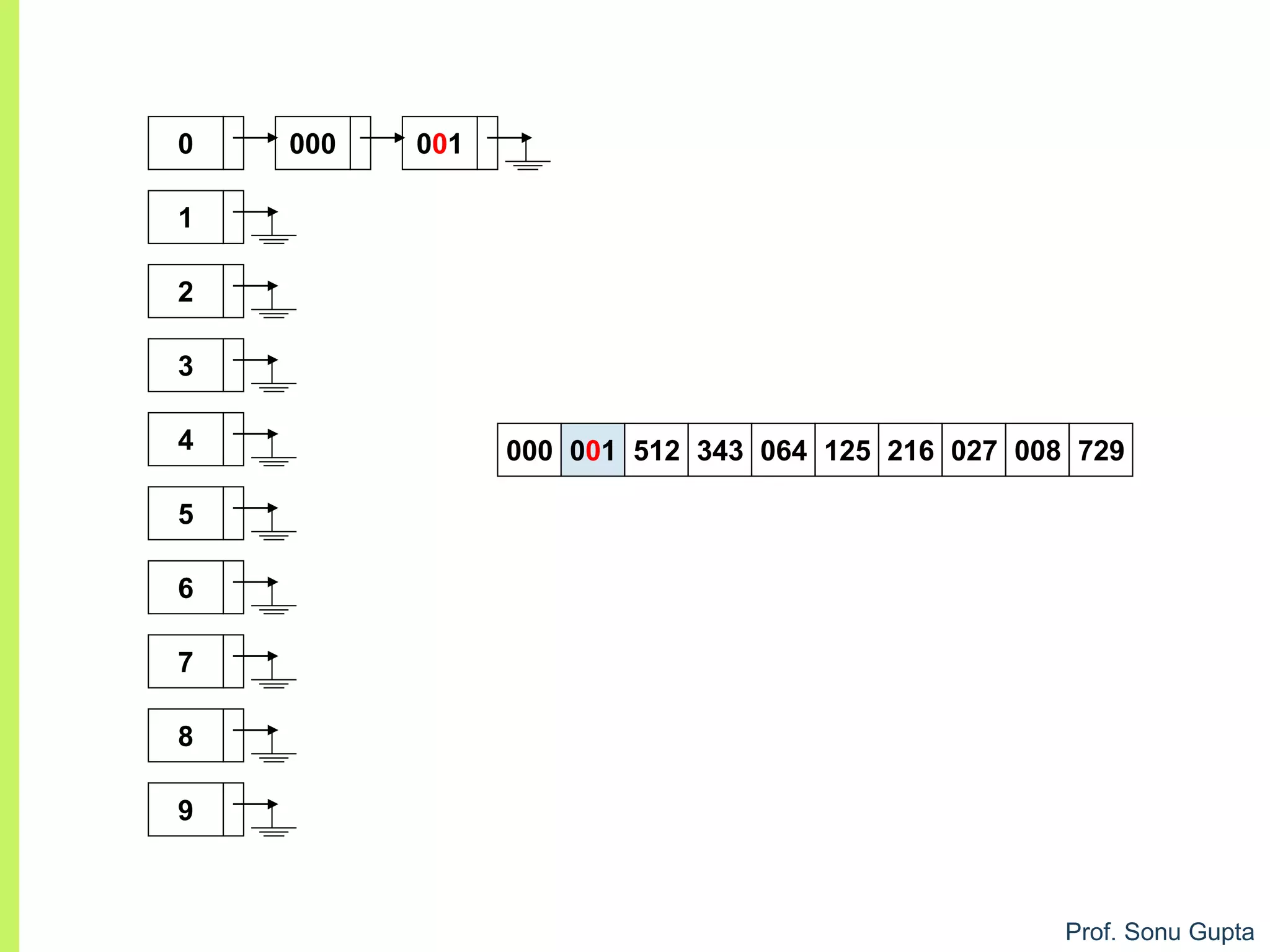
Prof. Sonu Gupta
000 001 512 343 064 125 216 027 008 729
1
2
3
4
5
6
7
8
9
0 001000

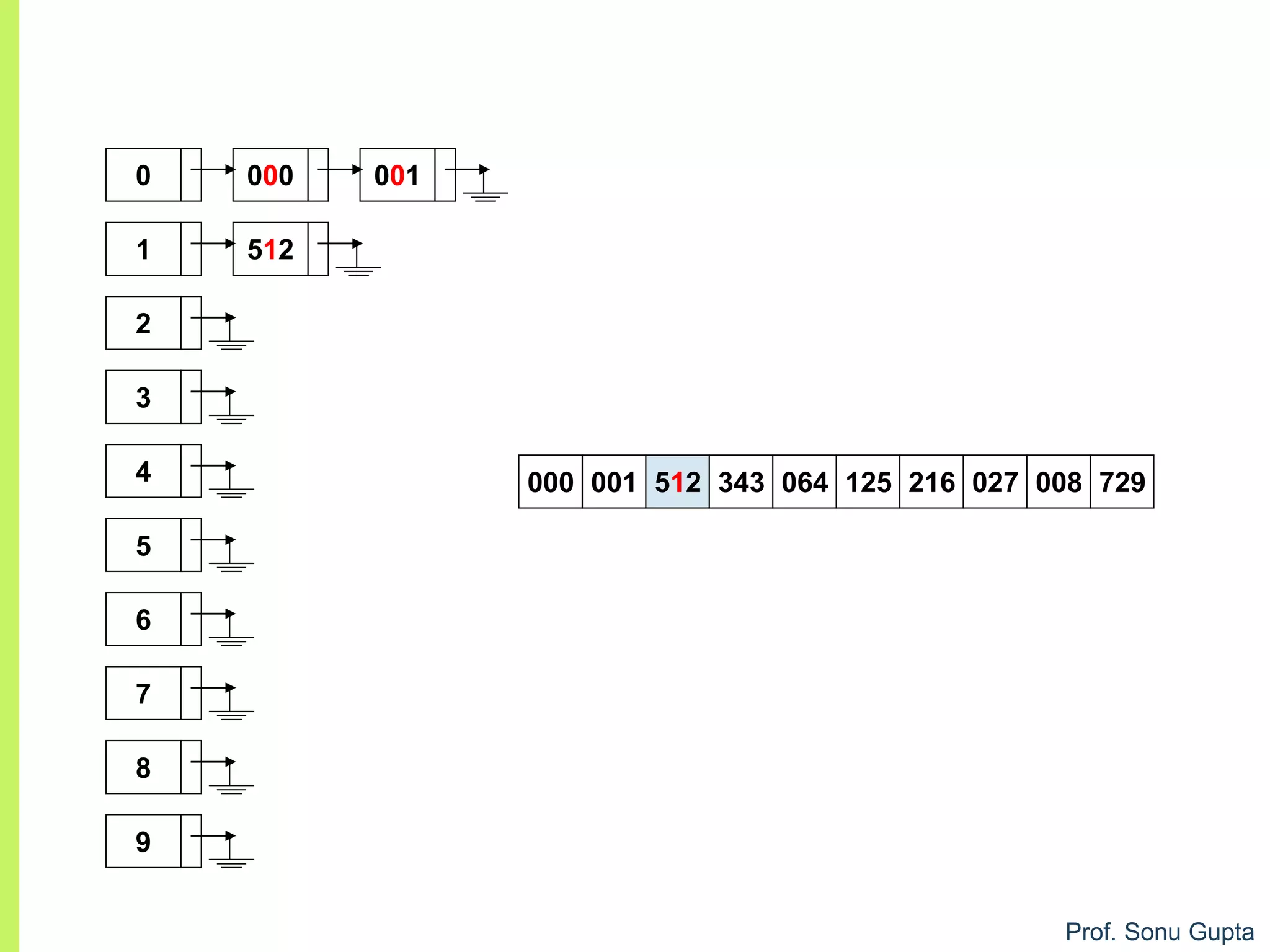
Prof. Sonu Gupta
000 001 512 343 064 125 216 027 008 729
2
3
4
5
6
7
8
9
0 001000
1 512

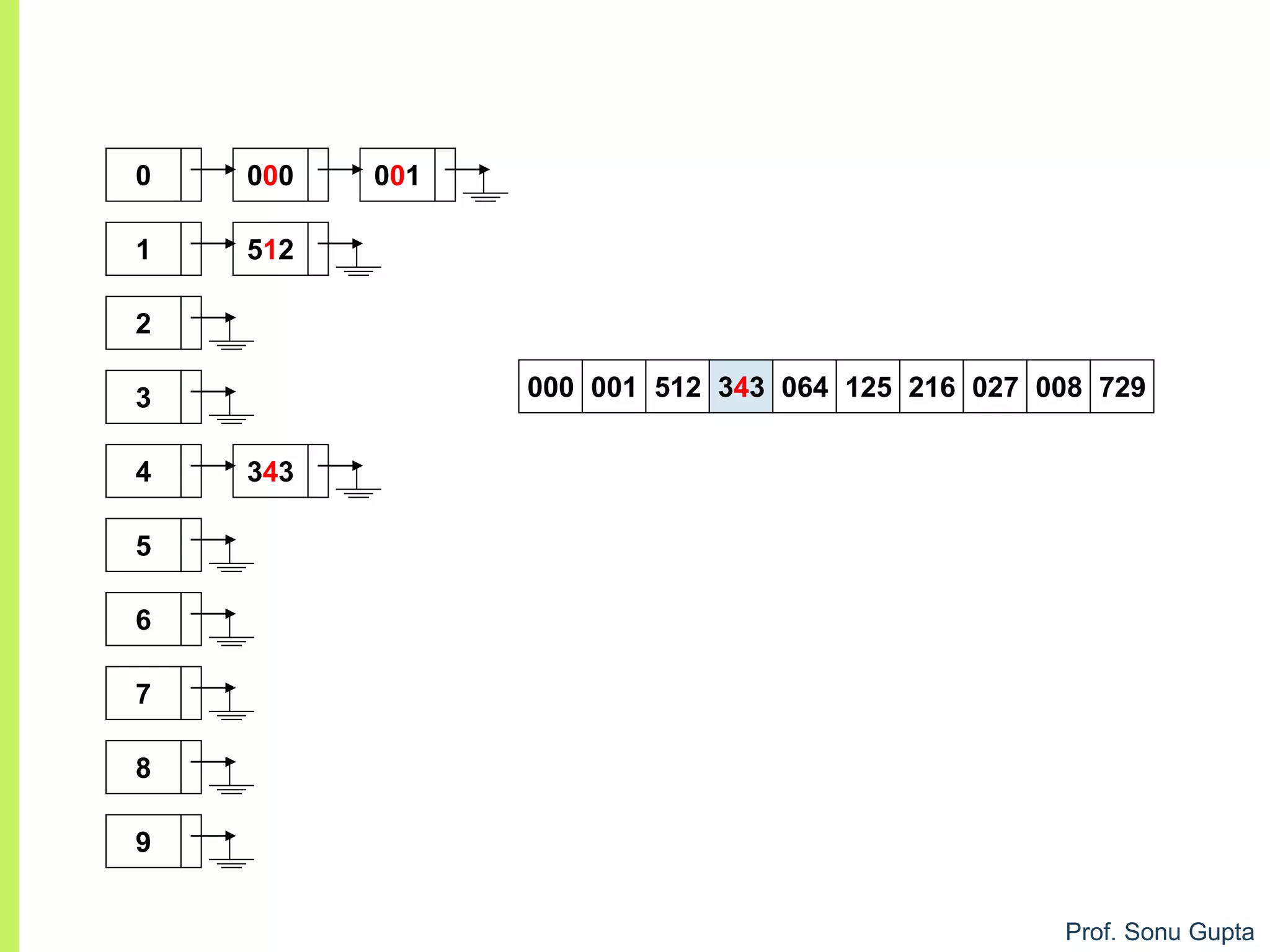
Prof. Sonu Gupta
000 001 512 343 064 125 216 027 008 729
2
3
5
6
7
8
9
0 001000
1 512
4 343

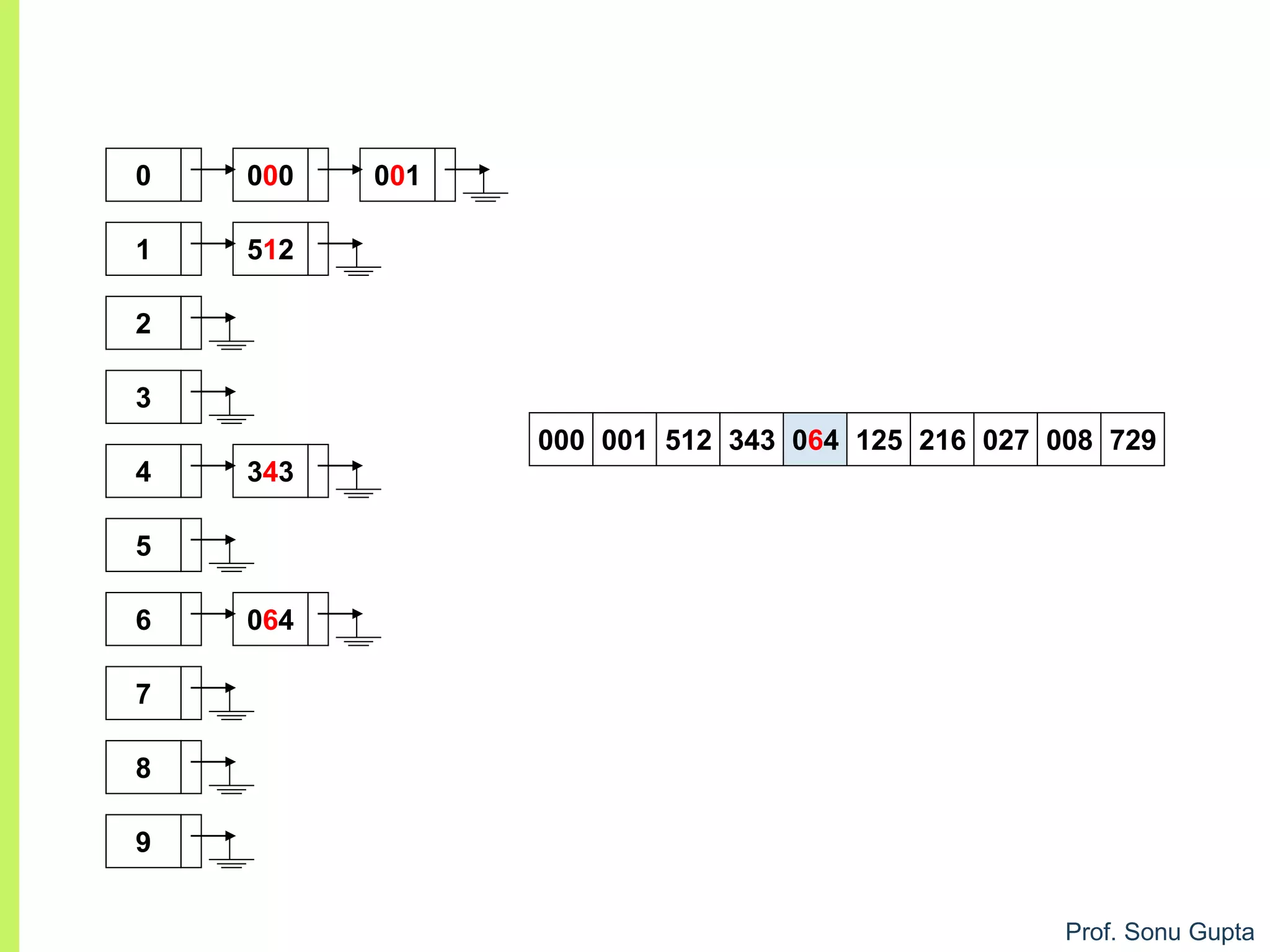
Prof. Sonu Gupta
000 001 512 343 064 125 216 027 008 729
2
3
5
7
8
9
0 001000
1 512
4 343
6 064

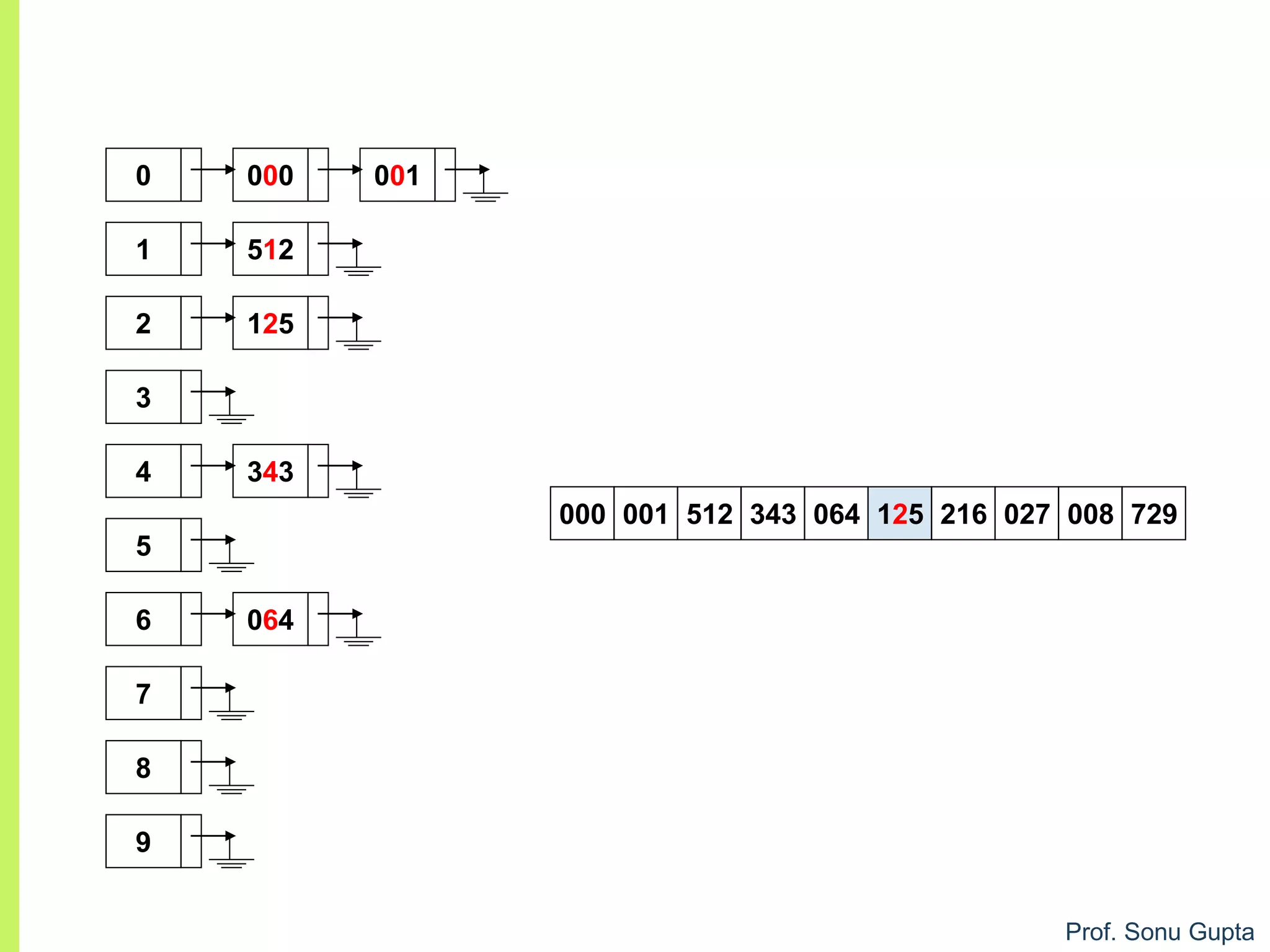
Prof. Sonu Gupta
000 001 512 343 064 125 216 027 008 729
3
5
7
8
9
0 001000
1 512
4 343
6 064
2 125

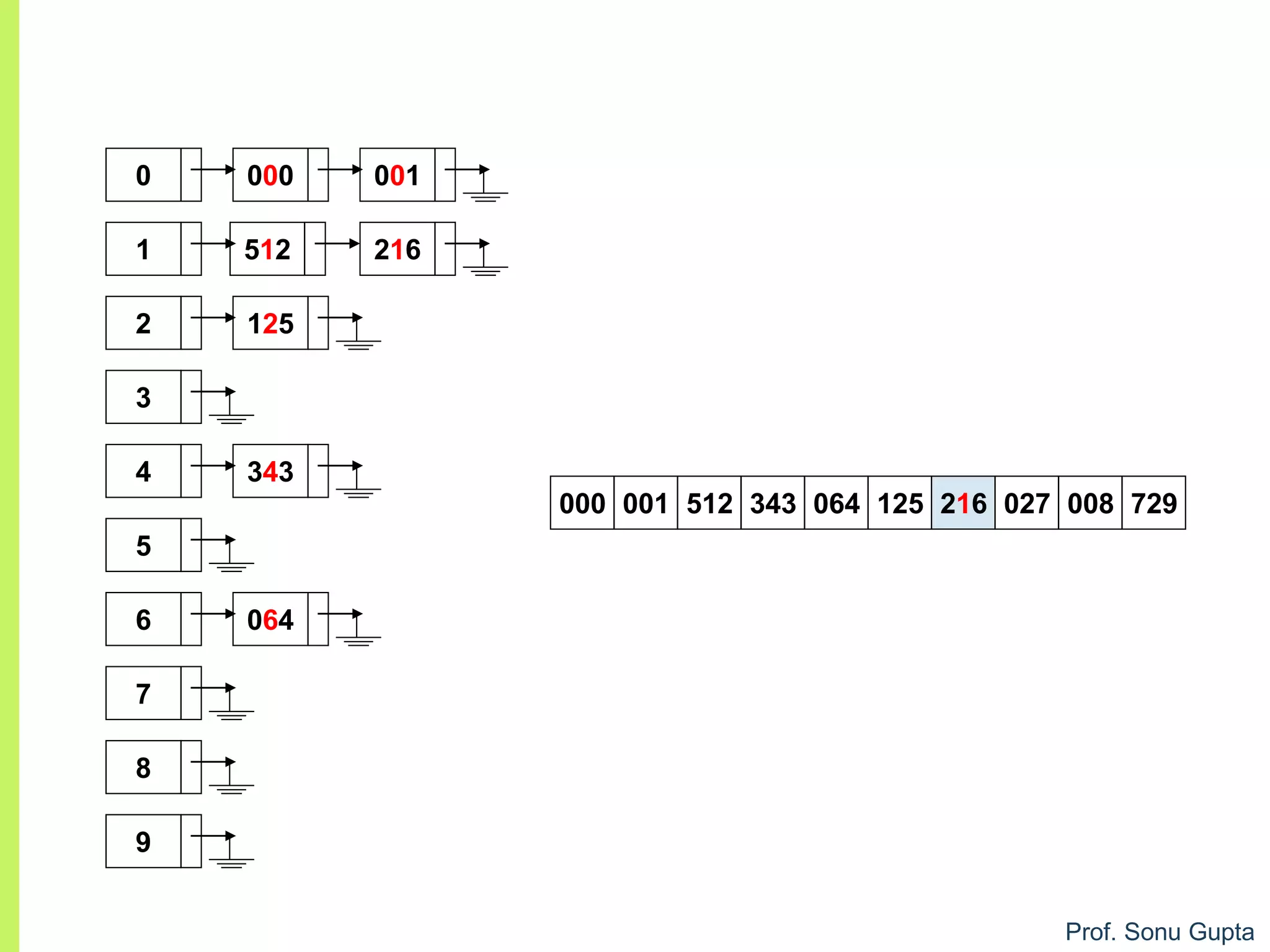
Prof. Sonu Gupta
000 001 512 343 064 125 216 027 008 729
3
5
7
8
9
0 001000
1 216
4 343
6 064
2 125
512

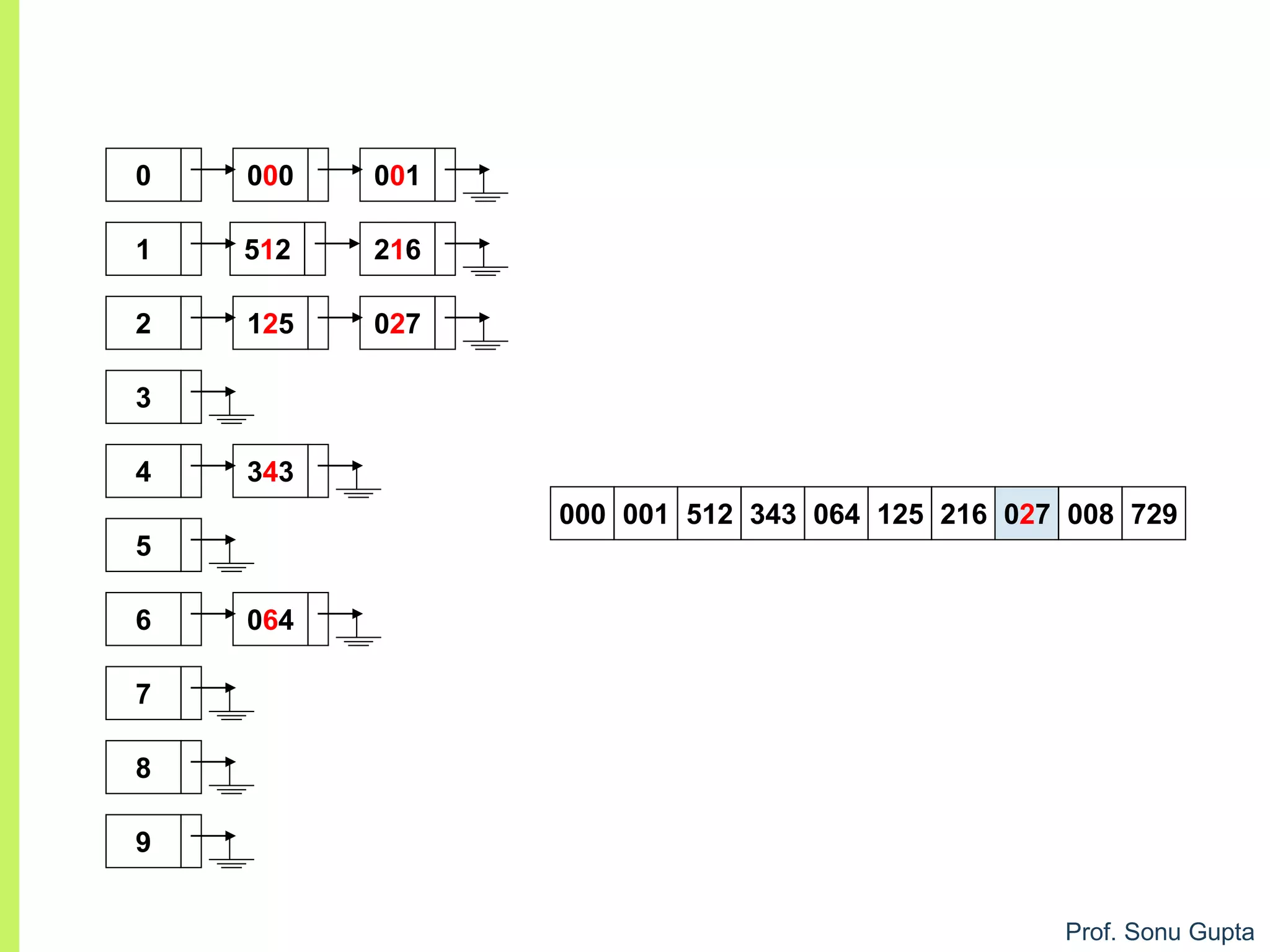
Prof. Sonu Gupta
000 001 512 343 064 125 216 027 008 729
3
5
7
8
9
0 001000
1 216
4 343
6 064
2 027
512
125

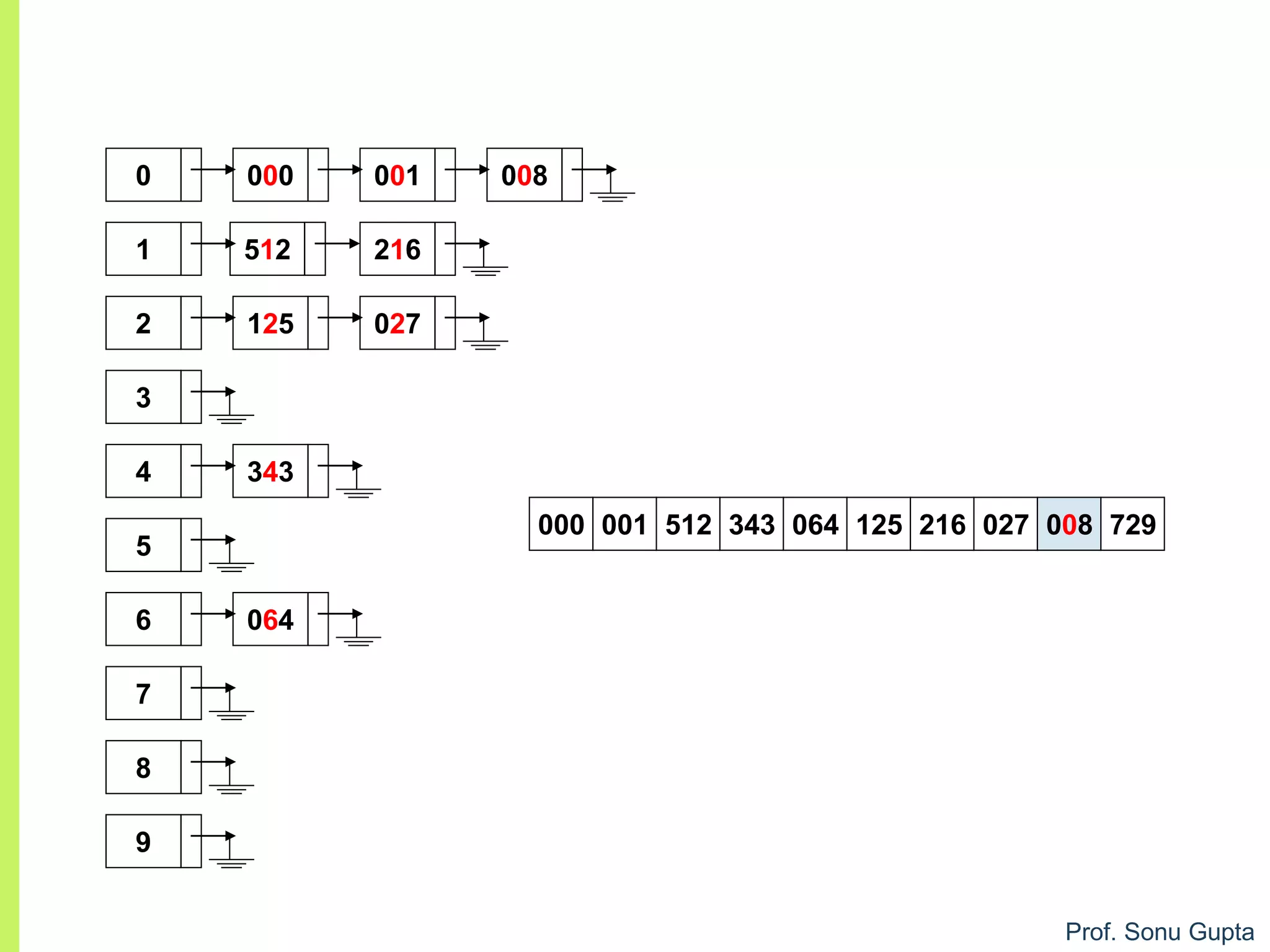
Prof. Sonu Gupta
000 001 512 343 064 125 216 027 008 729
3
5
7
8
9
0 008000
1 216
4 343
6 064
2 027
512
125
001

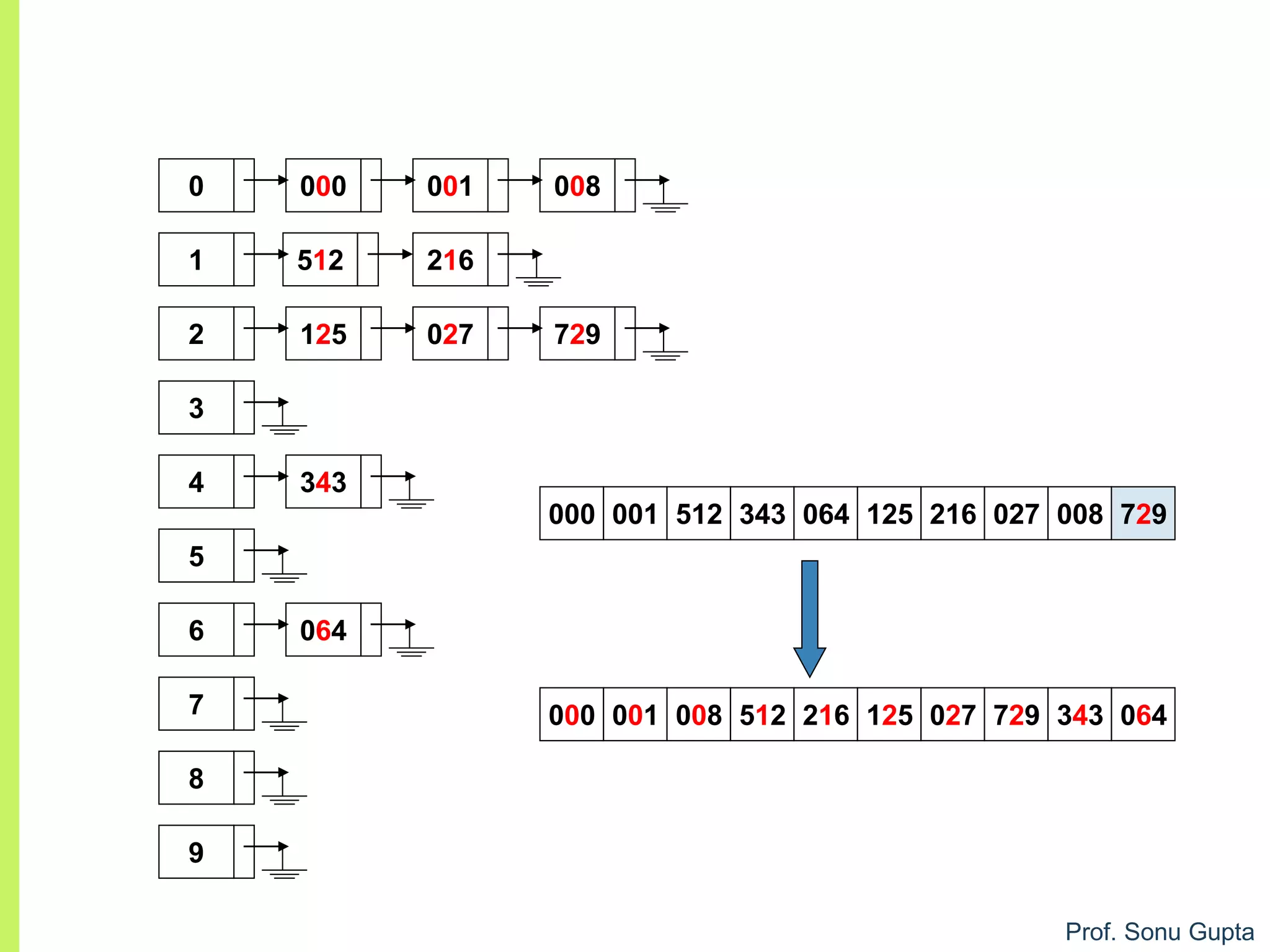
Prof. Sonu Gupta
000 001 512 343 064 125 216 027 008 729
3
5
7
8
9
0 008000
1 216
4 343
6 064
2 729
512
125
001
027
000 001 008 512 216 125 027 729 343 064

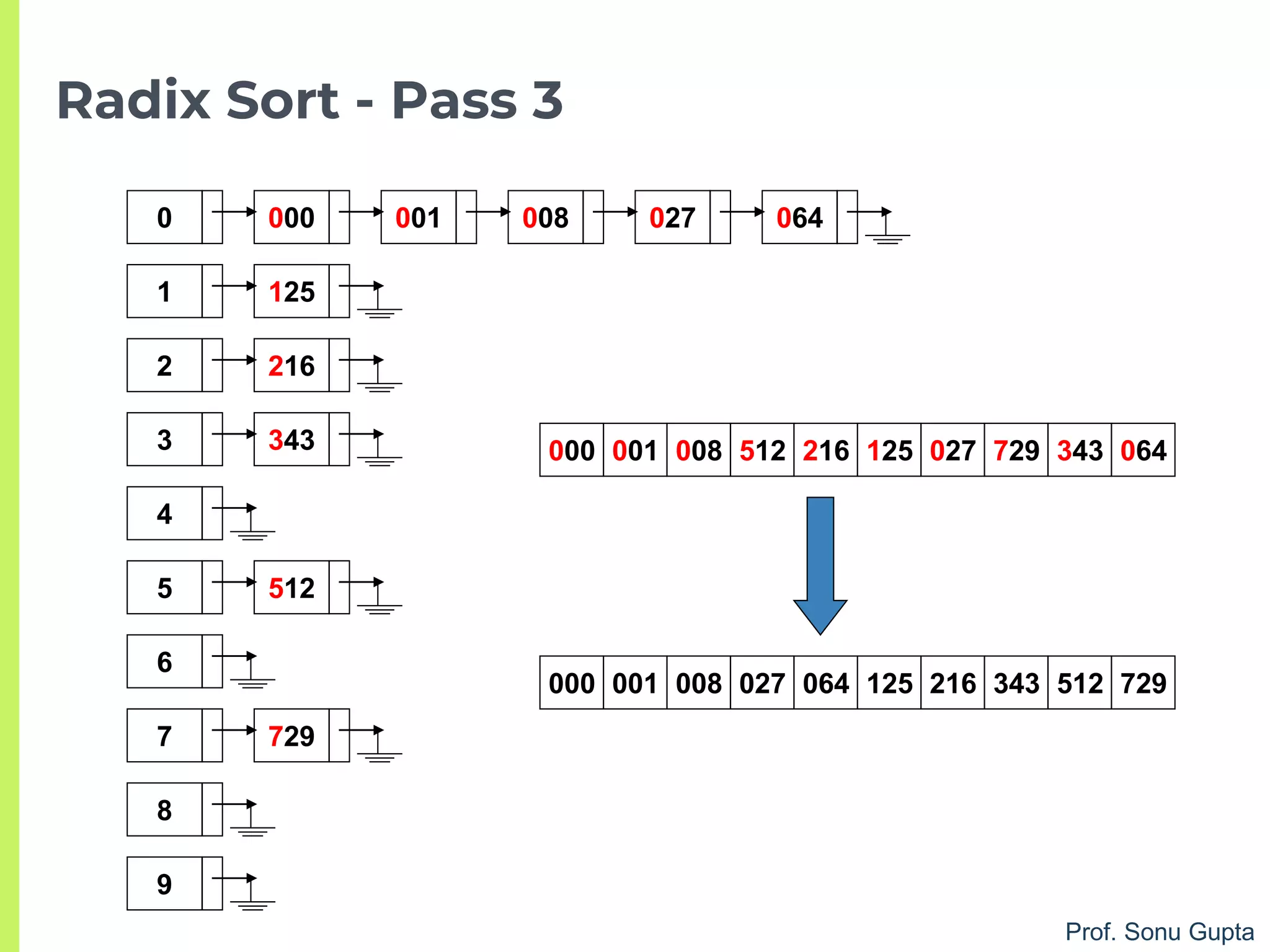
Prof. Sonu Gupta
Radix Sort - Pass 3
000 001 008 512 216 125 027 729 343 064
8
9
4
6
0 064000 001
5 512
2 216
1 125
008
7 729
3 343
027
000 001 008 027 064 125 216 343 512 729

Prof. Sonu Gupta
void arr :: sort(){
int bucket[10][10], buck_count[10];
int i,j,k,r,passes=0,divisor=1,largest,pass_no;
largest=a[0]; //Find the largest Number
for(i=1;i<n;i++)
if(a[i] > largest) largest=a[i];
while(largest > 0) //Find number of digits in largest number
{ passes++; largest = largest /10; }
for(pass_no=0; pass_no < passes; pass_no++)
{
for(k=0; k<10; k++) buck_count[k]=0; //Initialize bucket count
for(i=0;i<n;i++) //divide elements in bucket
{
r=(a[i]/divisor) % 10;
bucket[r][buck_count[r]]=a[i];
buck_count[r]++;
}
i=0; //collect elements from bucket
for(k=0; k<10; k++)
for(j=0; j<buck_count[k]; j++)
a[i++] = bucket[k][j];
divisor = divisor * 10;

Prof. Sonu Gupta
0 1 2 3 4 5 6 7 8 9
0
1
2
3
4
5
6
7
8
9
bucket[10][10]
0 0
1 0
2 0
3 0
4 0
5 0
6 0
7 0
8 0
9 0
buck_count[10]
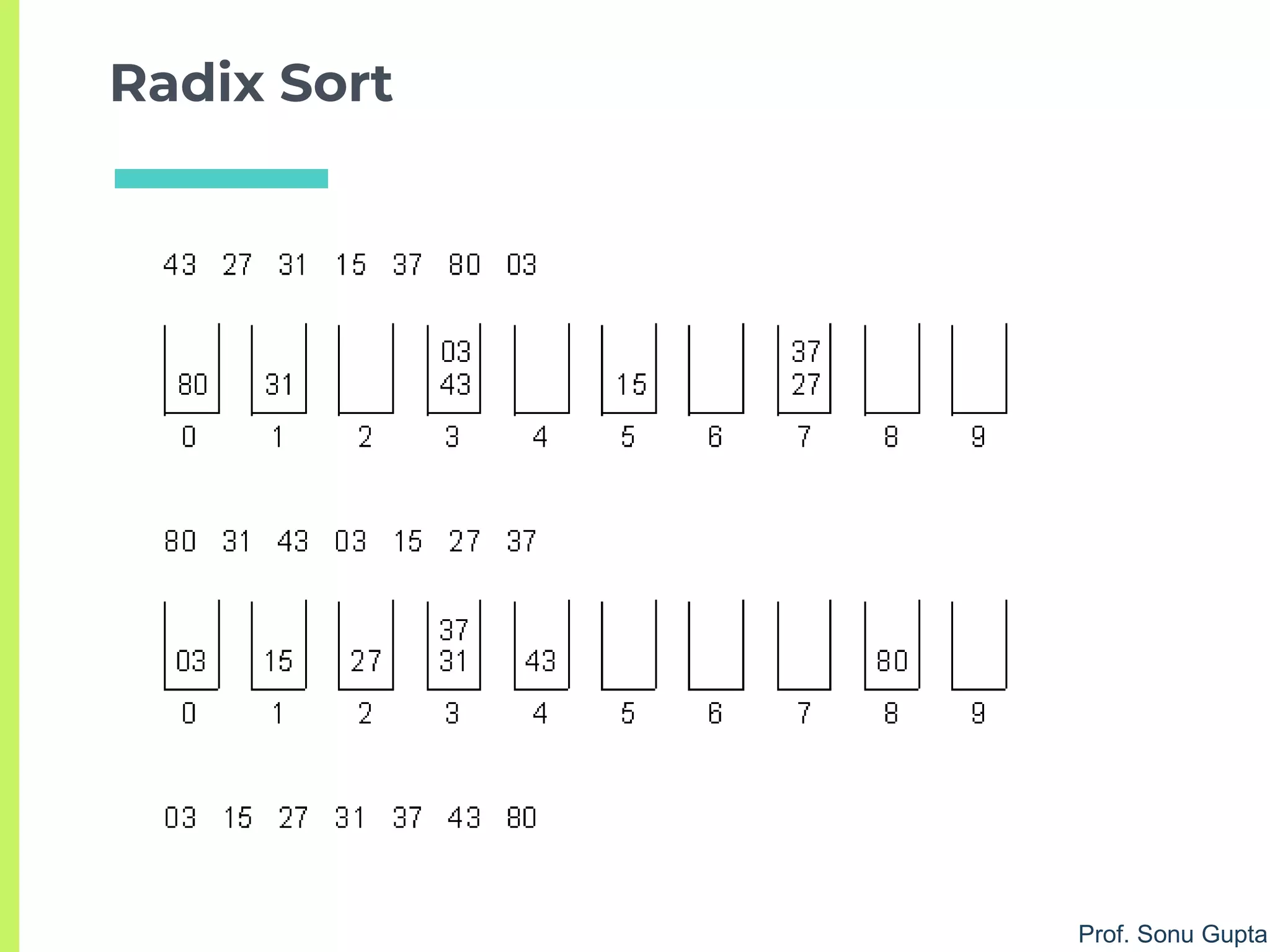
Largest = 80
Passes = 2
Initially

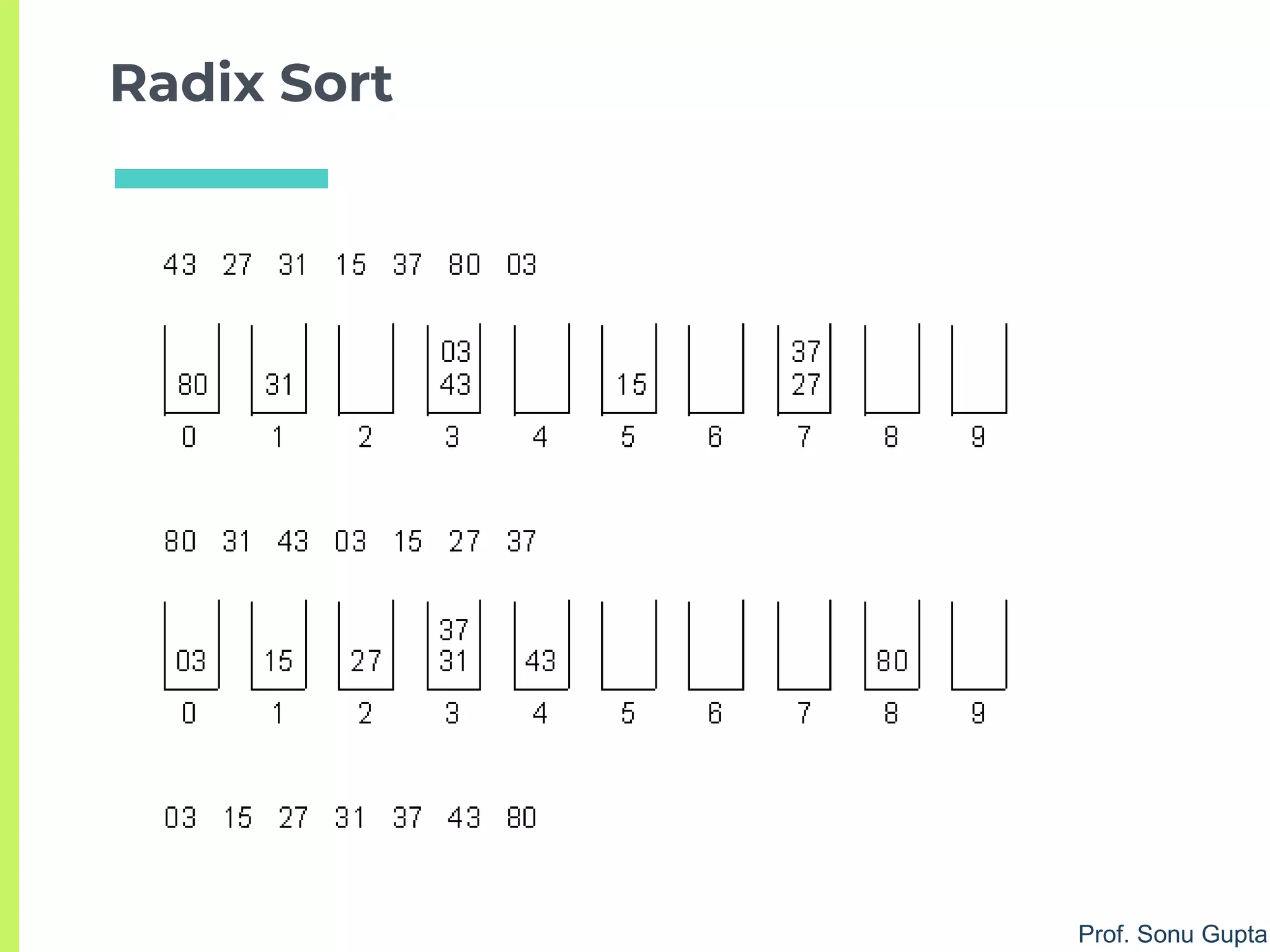
Prof. Sonu Gupta
0 1 2 3 4 5 6 7 8 9
0 80
1 31
2
3 43 03
4
5 15
6
7 27 37
8
9
bucket[10][10]
0 1
1 1
2 0
3 2
4 0
5 1
6 0
7 2
8 0
9 0
buck_count[10]
After Pass 1
a[i] = [80, 31, 43, 03, 15, 27, 37]

Prof. Sonu Gupta
0 1 2 3 4 5 6 7 8 9
0 03
1 15
2 27
3 31 37
4 43
5
6
7
8 80
9
bucket[10][10]
0 1
1 1
2 1
3 2
4 1
5
6
7
8 1
9
buck_count[10]
After Pass 2
a[i] = [03, 15, 27, 31, 37, 43, 80]
a[i] = [80, 31, 43, 03, 15, 27, 37]

Prof. Sonu Gupta
Complexity
 Complexity
 O (m * n) m is no. of digits, n no. of elements
 Memory
 Requires additional space
 Disadvantage – For every different type of data or sort
order, sort needs to rewritten.

Sorting algorithms

More Related Content

Similar to Sorting algorithms

Recently uploaded

Sorting algorithms