CHAPTER 2 Simple Sorting Algorithms (1).pptx

CHAPTER 2:
Simple Searching and
Sorting Algorithms

OUTLINE
Searching Algorithms
 Linear Search
 Binary Search
Sorting Algorithms
 Bubble Sort
 Insertion Sort
 Selection Sort
 Pointer Sort

Sorting Algorithms
What is Sorting?
• A Sorting Algorithm is used to rearrange a given array or list of
elements according to a comparison operator on the elements.
• The comparison operator is used to decide the new order of
elements in the respective data structure.
For Example: The below list of characters is sorted in increasing order of their ASCII values.

Sorting Algorithms
That is, the character with a lesser ASCII value will be placed first than
the character with a higher ASCII value.

1) Bubble Sort
Bubble Sort: is the simplest sorting algorithm that works by repeatedly
swapping the adjacent elements if they are in the wrong order.
In Bubble Sort algorithm,
• traverse from left and compare adjacent elements and the higher
one is placed at right side.
• In this way, the largest element is moved to the rightmost end at
first.
• This process is then continued to find the second largest and place it
and so on until the data is sorted.

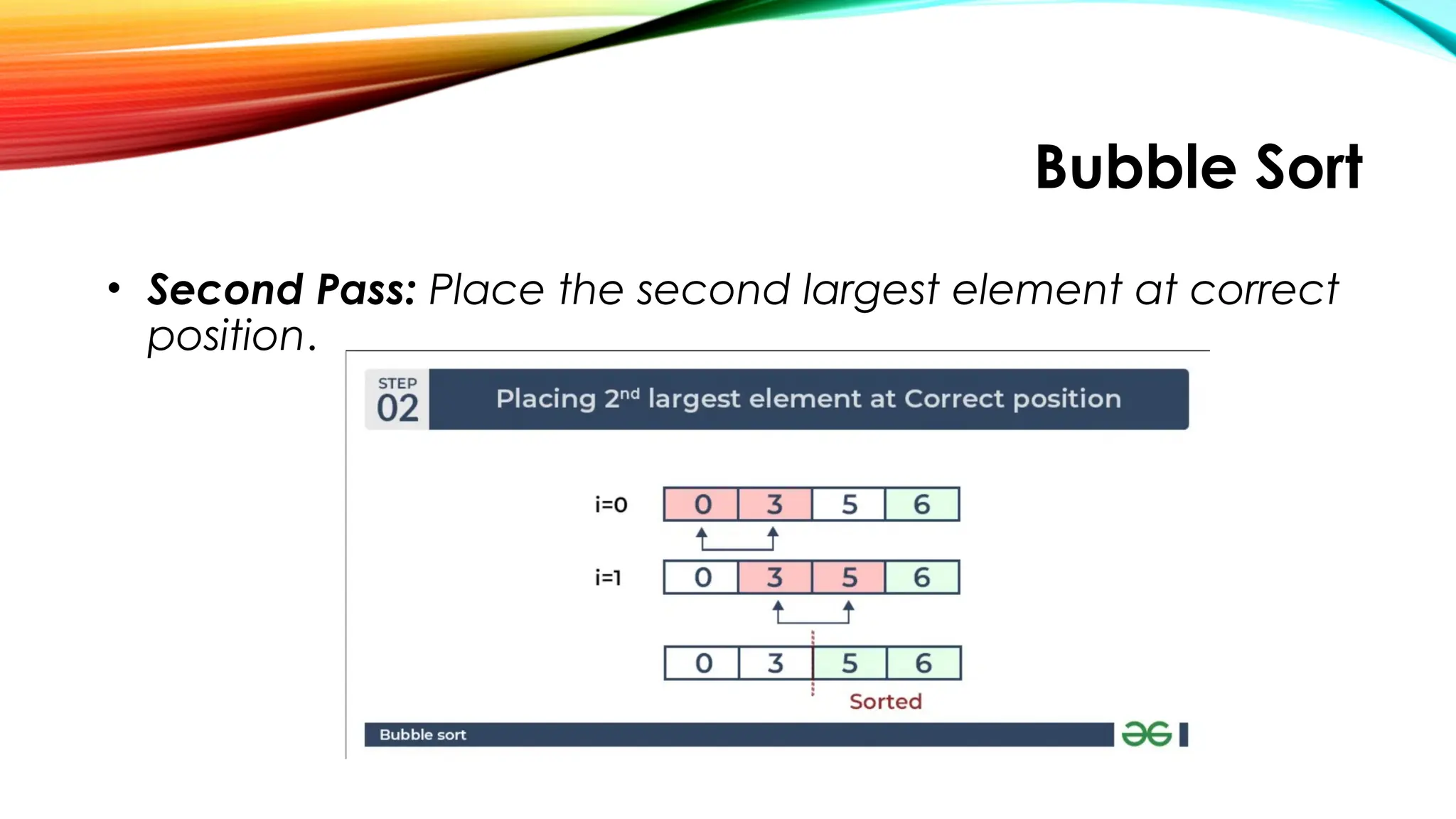
Bubble Sort
• Consider a list(array): Input: arr[] = {6, 0, 3, 5}
• First Pass:
• The largest element is placed in its correct position, i.e., at
the end of the array.

Bubble Sort
• Second Pass: Place the second largest element at correct
position.

Bubble Sort
• Third Pass: Place the third largest element at correct
position.

Bubble Sort
Pseudocode
void bubbleSort(int numbers[], intarray_size){
inti, j, temp;
for (i = (array_size - 1); i>= 0; i--)
for (j = 1; j <= i; j++)
if (numbers[j-1] > numbers[j]){
temp = numbers[j-1];
numbers[j-1] = numbers[j];
numbers[j] = temp;
}
}

Bubble Sort
• Total no. of passes  n-1
• Total no. of comparisons  n*(n-1)/2
Complexity Analysis of Bubble Sort:
• Time Complexity: O(N2
)
Auxiliary Space: O(1)

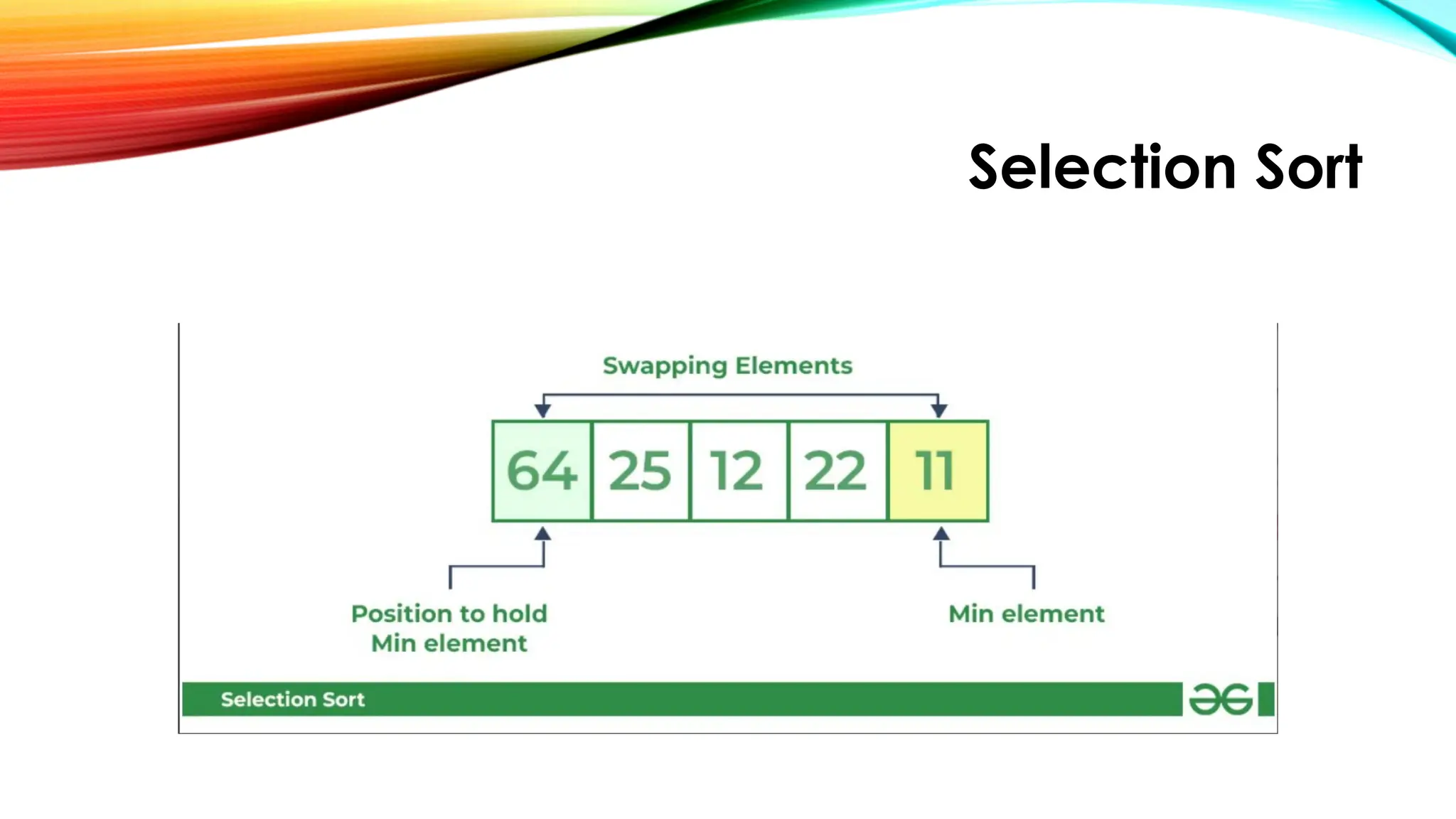
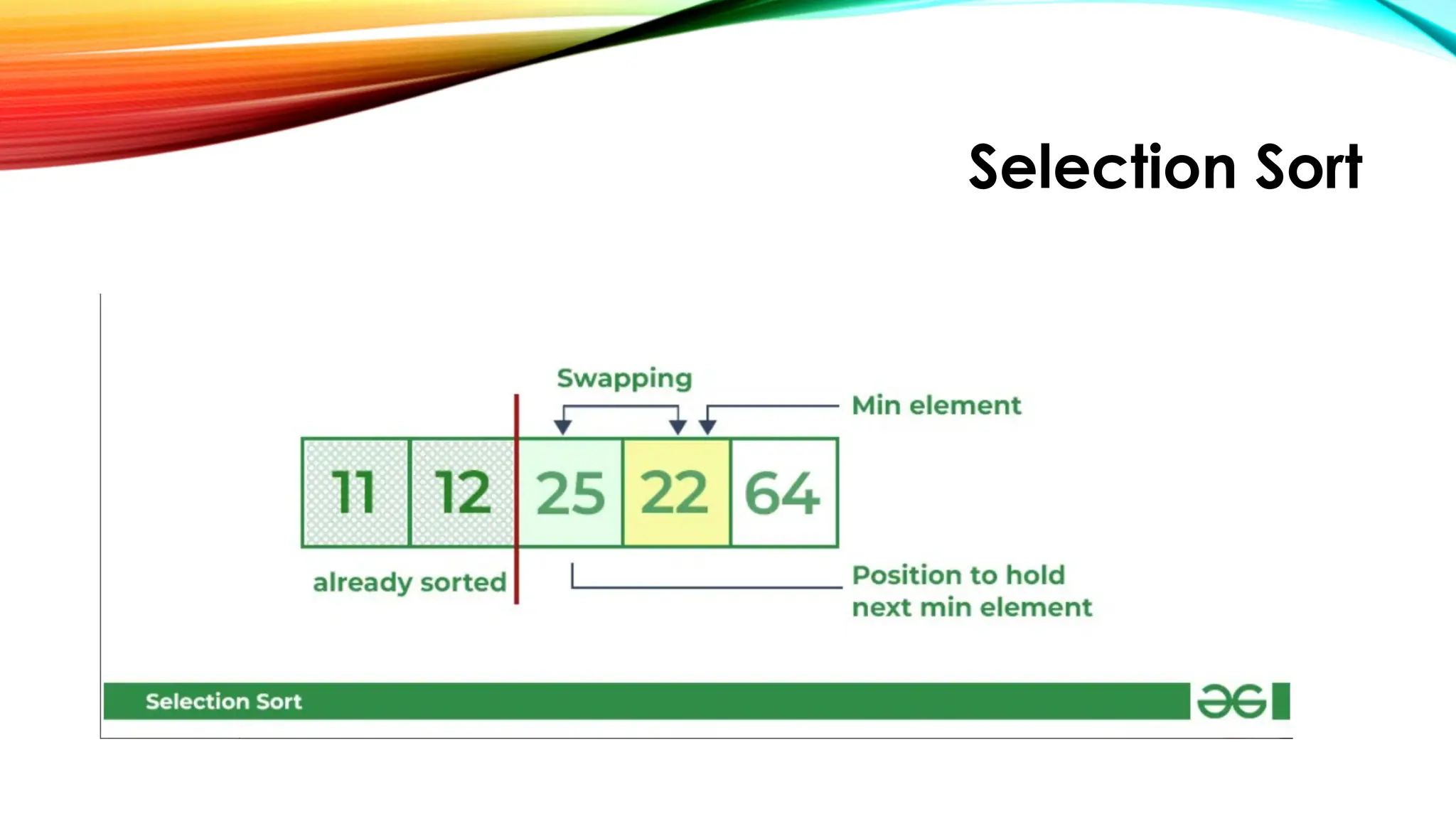
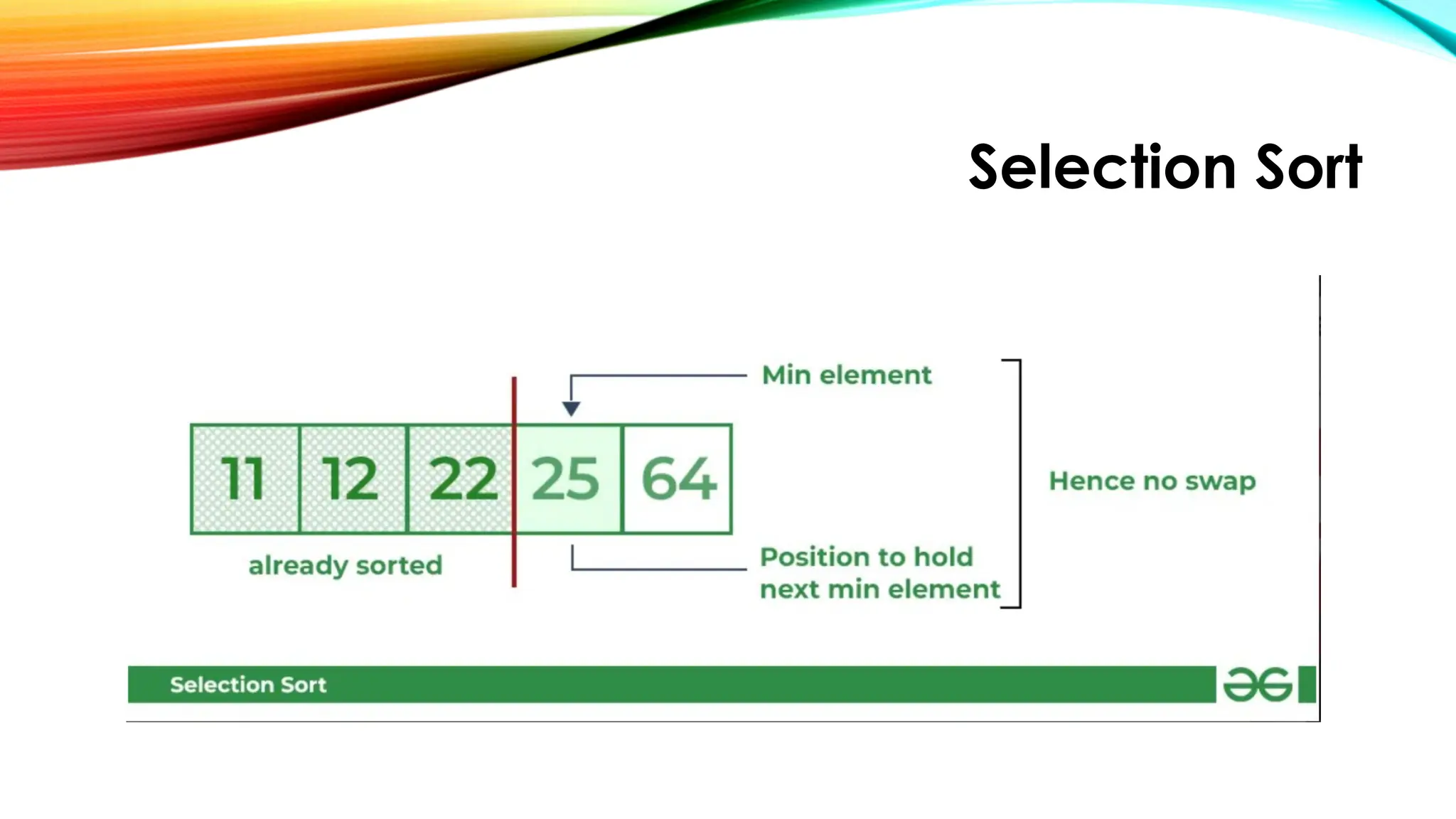
2) Selection Sort
• Selection sort is a simple and efficient sorting algorithm that works by
repeatedly selecting the smallest (or largest) element from the unsorted
portion of the list and moving it to the sorted portion of the list.
• The algorithm repeatedly selects the smallest (or largest) element from the
unsorted portion of the list and swaps it with the first element of the
unsorted part. This process is repeated for the remaining unsorted portion
until the entire list is sorted.

Selection Sort
Lets consider the following array as an example: arr[] = {64, 25, 12, 22, 11}
First pass:
• For the first position in the sorted array, the whole array is traversed
from index 0 to 4 sequentially. The first position where 64 is stored
presently, after traversing whole array it is clear that 11 is the lowest
value.
• Thus, replace 64 with 11. After one iteration 11, which happens to be
the least value in the array, tends to appear in the first position of the
sorted list.

Selection Sort
Second Pass:
• For the second position, where 25 is present, again traverse the rest of the
array in a sequential manner.
• After traversing, we found that 12 is the second lowest value in the array
and it should appear at the second place in the array, thus swap these
values.

Selection Sort
Third Pass:
• Now, for third place, where 25 is present again traverse the
rest of the array and find the third least value present in the
array.
• While traversing, 22 came out to be the third least value
and it should appear at the third place in the array, thus
swap 22 with element present at third position.

Selection Sort
Fourth pass:
• Similarly, for fourth position traverse the rest of the array
and find the fourth least element in the array
• As 25 is the 4th lowest value hence, it will place at the
fourth position.

Selection Sort
Fifth Pass:
• At last the largest value present in the array automatically get
placed at the last position in the array
• The resulted array is the sorted array.

Selection Sort
Pseudocode: Algorithm
1. Set MIN to location 0.
2. Search the minimum element in the list.
3. Swap with value at location MIN.
4. Increment MIN to point to next element.
5. Repeat until the list is sorted.

Selection Sort
Pseudocode: Algorithm Selection-Sort (A)
for( i = 0; i < n-1; i++)
min = i;
for (j = i + 1; j < n; j++)
if A[j] < A[min])
min = j;
if(min != i)
swap(A[i], A[min]);

Selection Sort
Time Complexity:
The time complexity of Selection Sort is O(N2
) as there are
two nested loops:

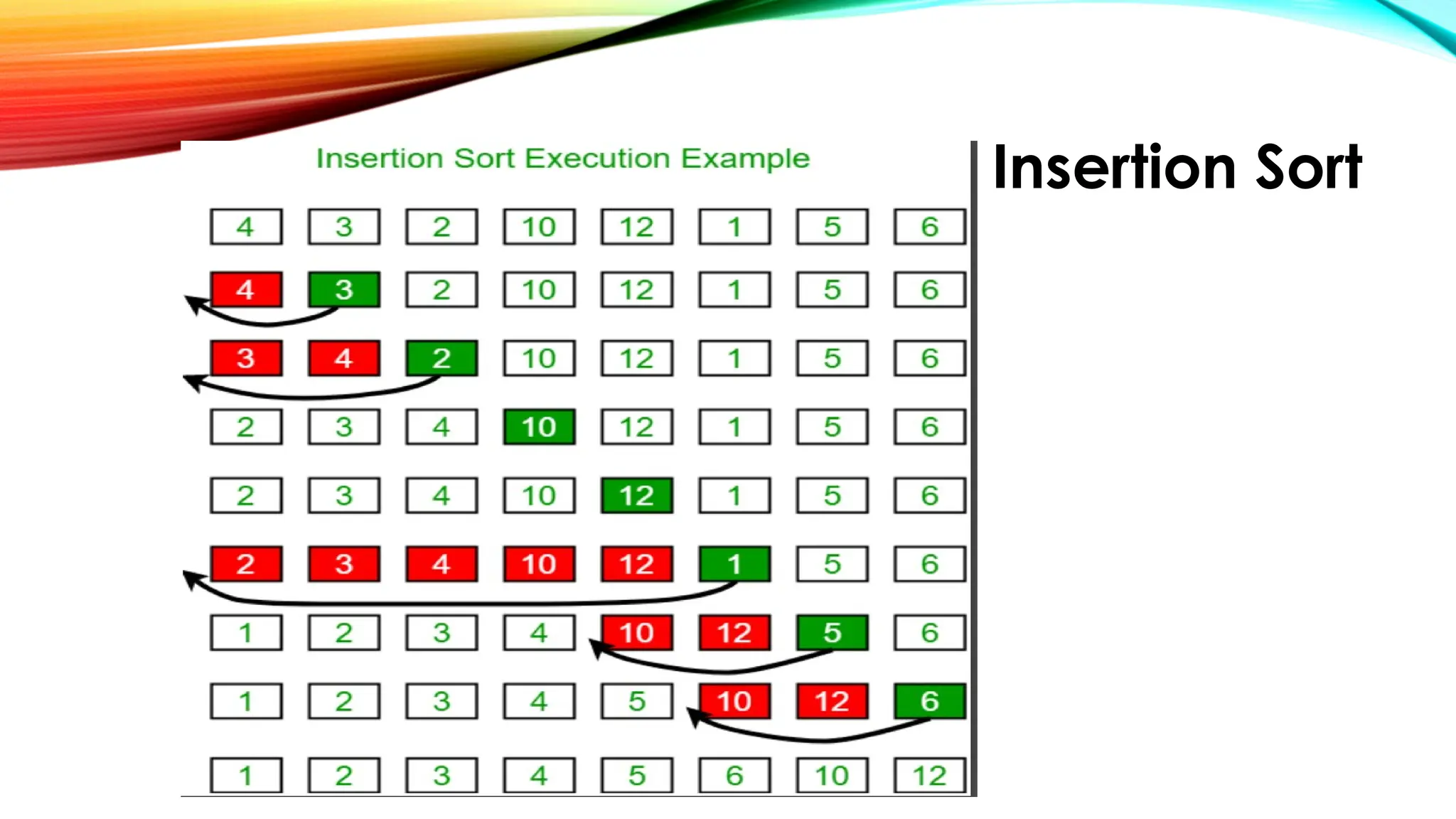
3) Insertion Sort
Insertion sort is a simple sorting algorithm that works similar
to the way you sort playing cards in your hands.
The array is virtually split into a sorted and an unsorted part.
Values from the unsorted part are picked and placed at
the correct position in the sorted part.

Insertion Sort
• Working of Insertion Sort algorithm:
• Consider an example: arr[]: {12, 11, 13, 5, 6}
First Pass:
Initially, the first two elements of the array are compared in insertion
sort.
12 11 13 5 6
12 11 13 5 6

Insertion Sort
• Here, 12 is greater than 11 hence they are not in the
ascending order and 12 is not at its correct position. Thus,
swap 11 and 12.
• So, for now 11 is stored in a sorted sub-array.
11 12 13 5 6

Insertion Sort
Second Pass:
Now, move to the next two elements and compare them.
Here, 13 is greater than 12, thus both elements seems to be in
ascending order, hence, no swapping will occur. 12 also stored in a
sorted sub-array along with 11.
11 12 13 5 6
11 12 13 5 6

Insertion Sort
Third Pass:
• Now, two elements are present in the sorted sub-array
which are 11 and 12.
• Moving forward to the next two elements which are 13
and 5.
• Both 5 and 13 are not present at their correct place so swap them.
11 12 13 5 6
11 12 5 13 6

Insertion Sort
• After swapping, elements 12 and 5 are not sorted, thus
swap again.
• Here, again 11 and 5 are not sorted, hence swap again.
• Here, 5 is at its correct position.
11 5 12 13 6
5 11 12 13 6

Insertion Sort
Fourth Pass:
• Now, the elements which are present in the sorted sub-array are 5,
11 and 12
• Moving to the next two elements 13 and 6.
• Clearly, they are not sorted, thus perform swap between both.
5 11 12 13 6
5 11 12 6 13

Insertion Sort
• Now, 6 is smaller than 12, hence, swap again.
• Here, also swapping makes 11 and 6 unsorted hence,
swap again.
• Finally, the array is completely sorted.
5 6 11 12 13
5 11 6 12 13

Insertion Sort
Pseudocode:
for i = 1 to length(A)-1:
j= i;
While j>0 and A[j-1] >A[j]
swap A[ j ] and A[ j-1]
j = j-1

Insertion Sort
Complexity of Insertion Sort:
It has a time complexity of O(n^2) in the worst case and
O(n) in the best case.
Application of Sorting Algorithms
• Order things by their value.
• The contact list on the phone.

CHAPTER 2 Simple Sorting Algorithms (1).pptx

More Related Content

Similar to CHAPTER 2 Simple Sorting Algorithms (1).pptx

More from shambelworku8

Recently uploaded

CHAPTER 2 Simple Sorting Algorithms (1).pptx

Editor's Notes