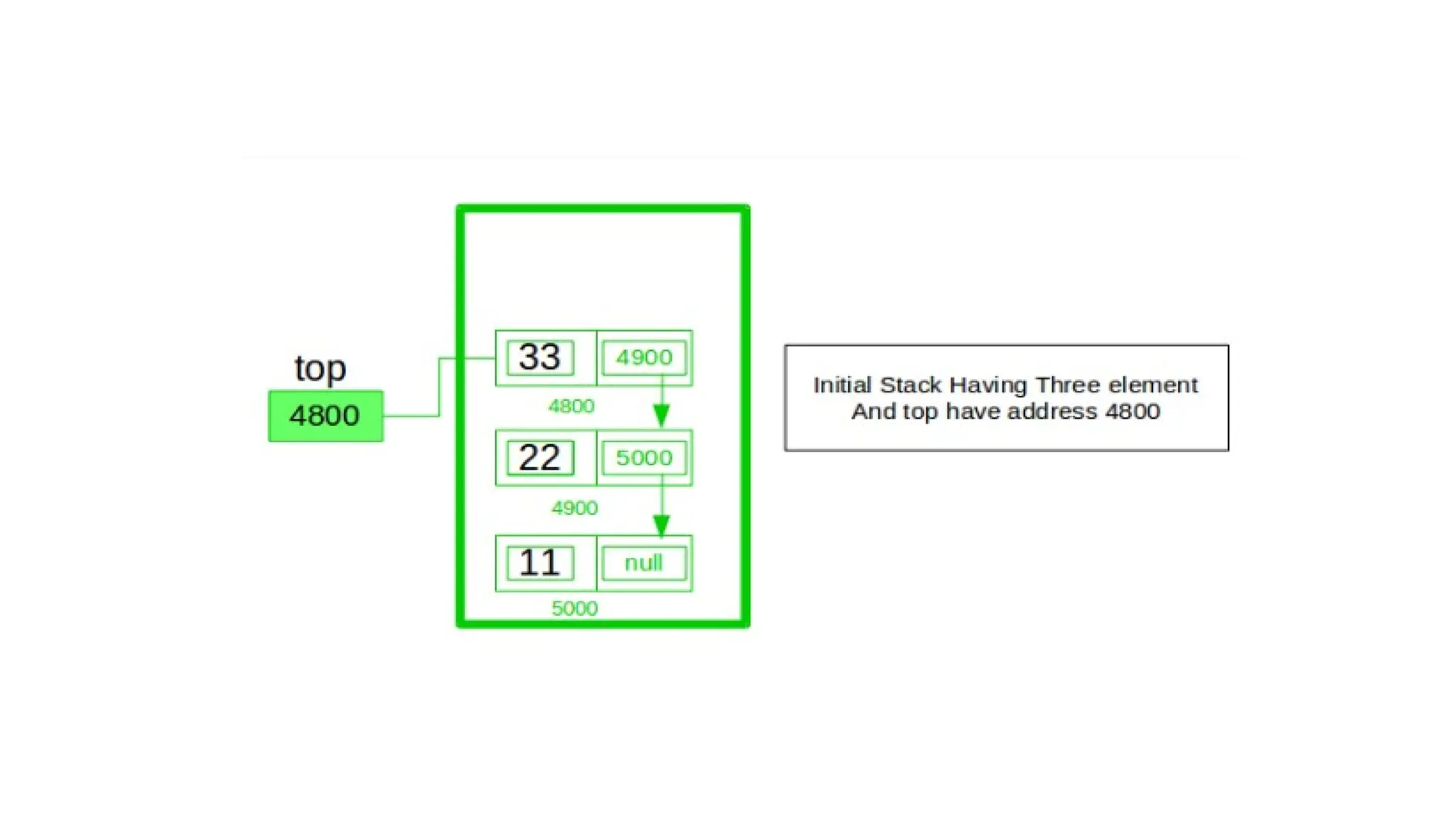
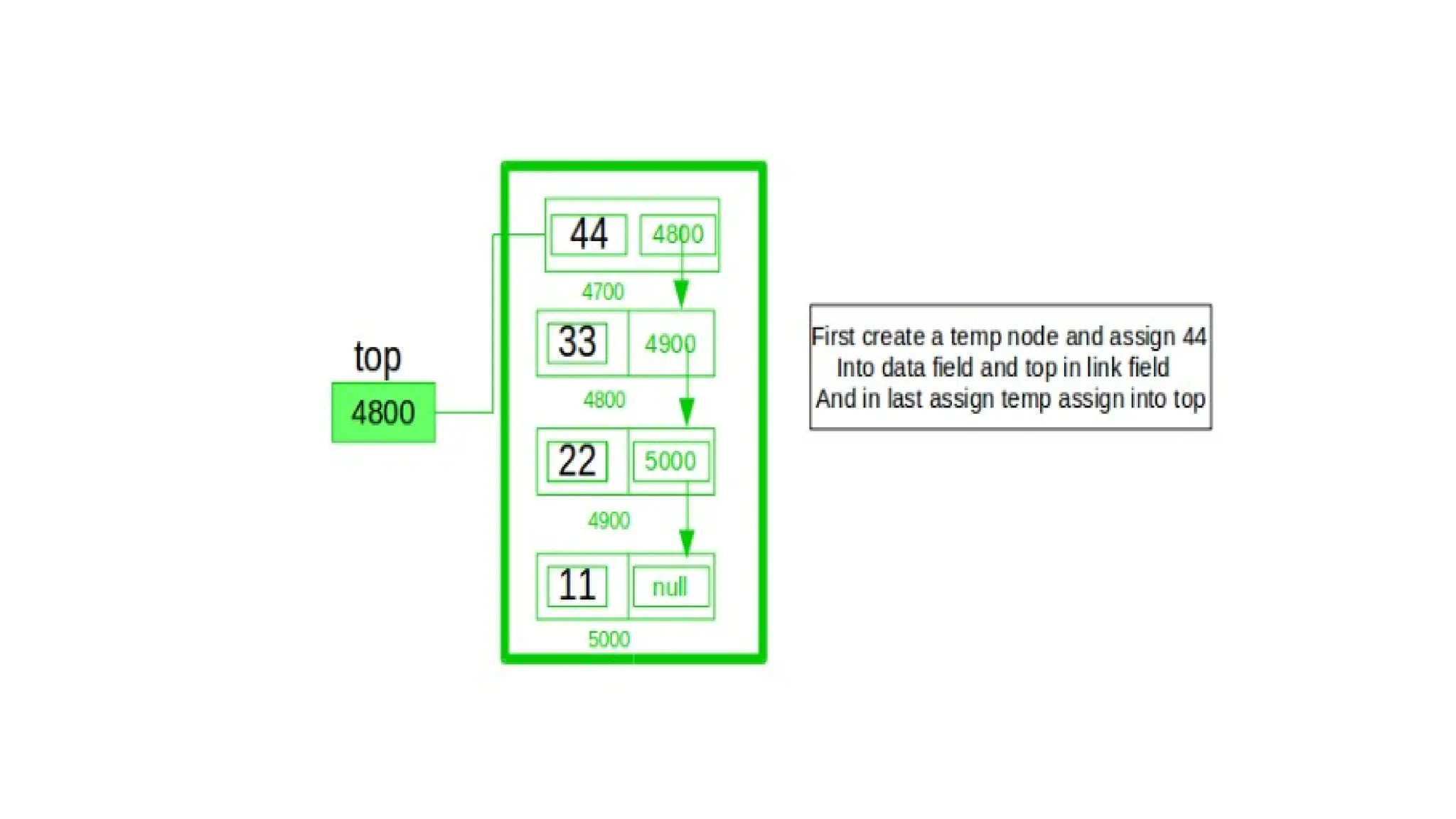
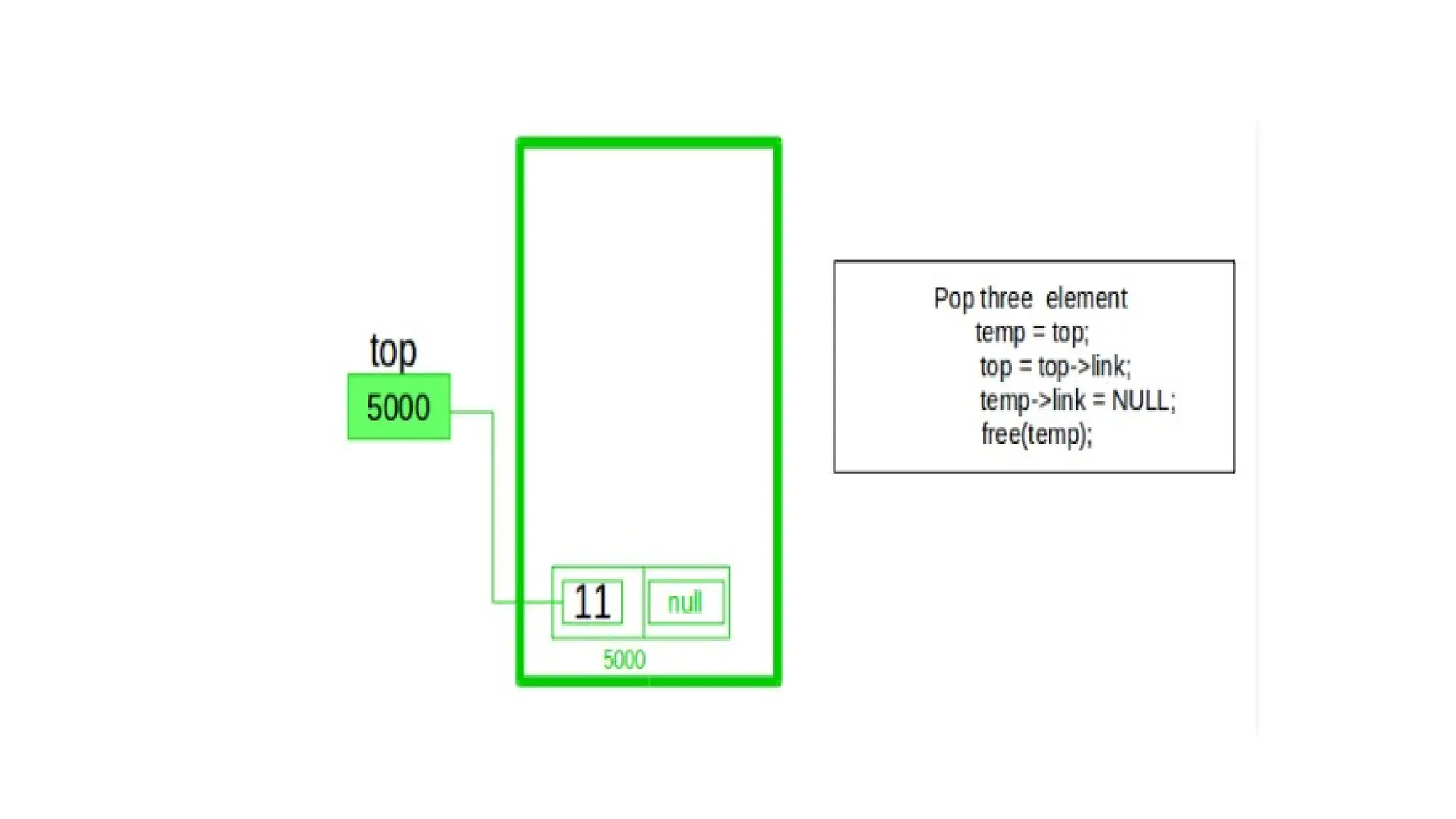
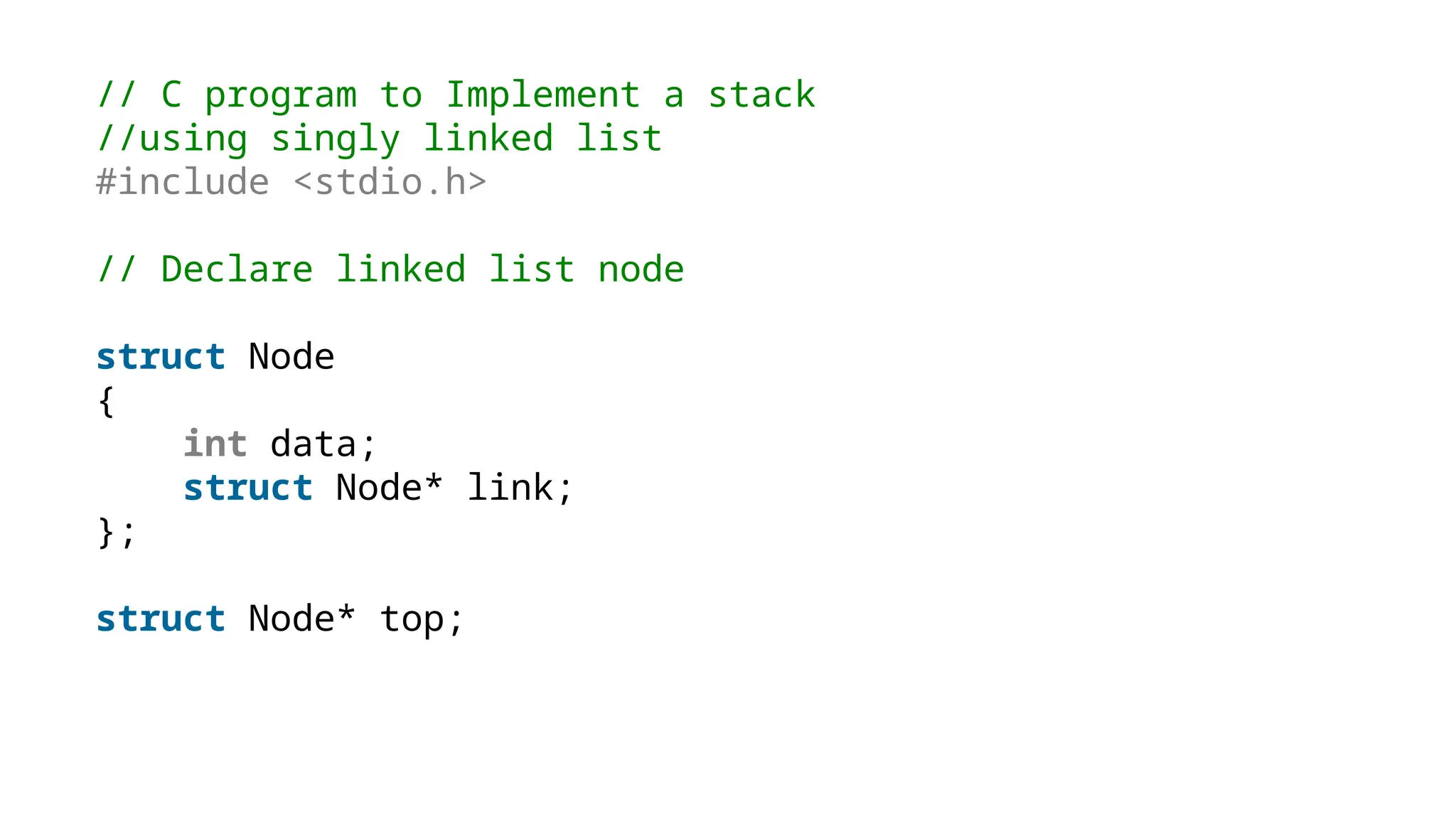
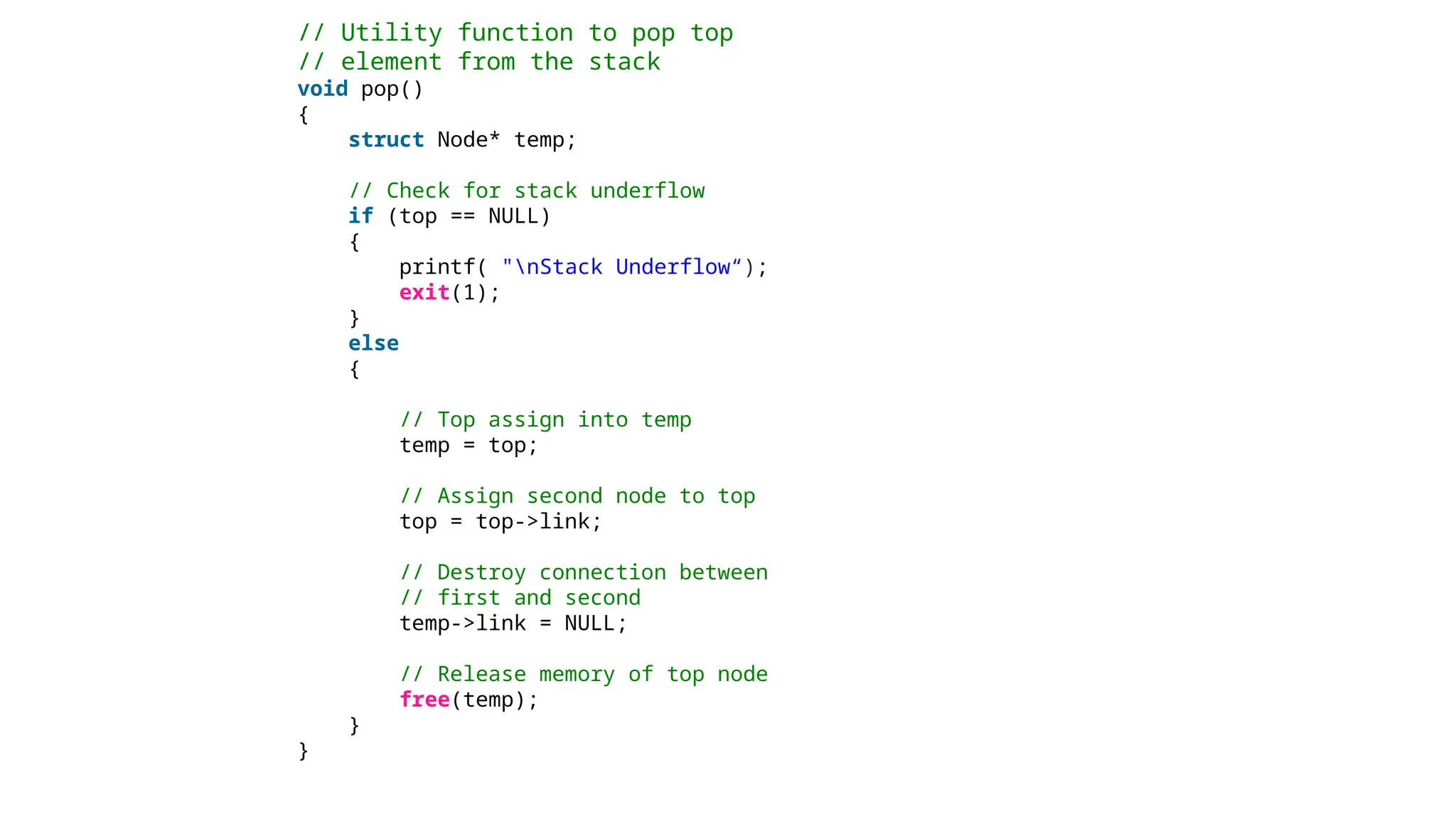
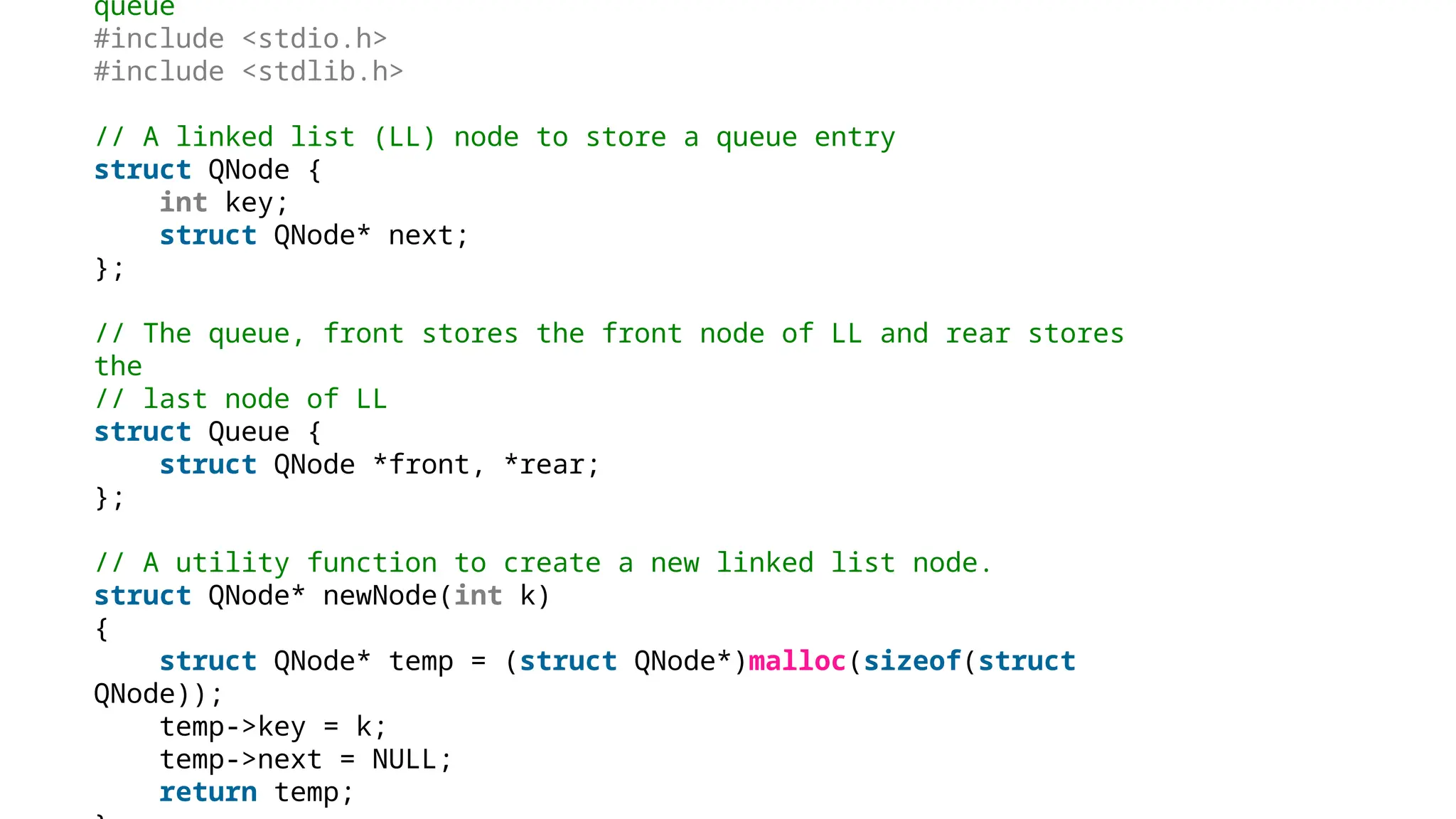
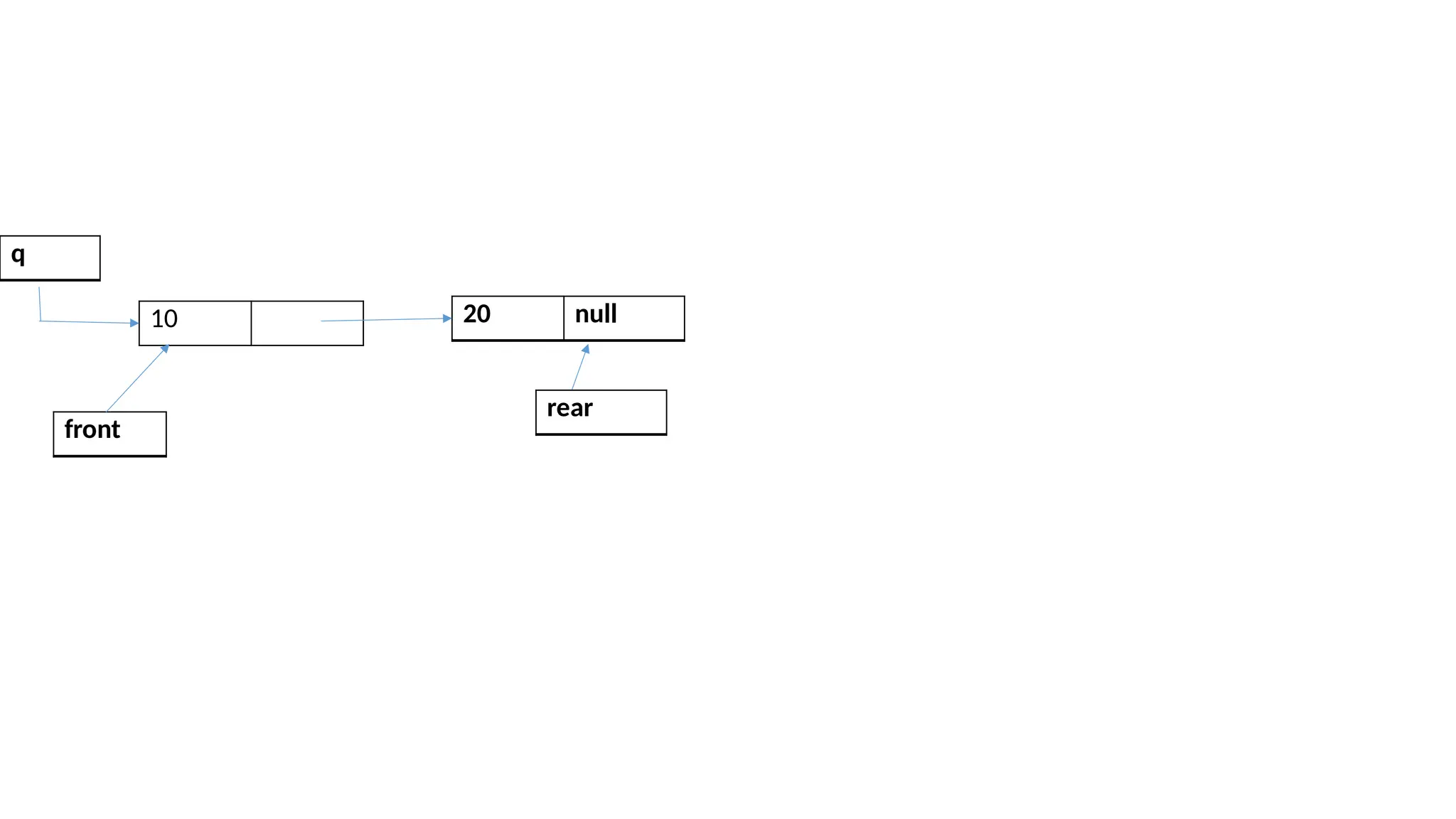
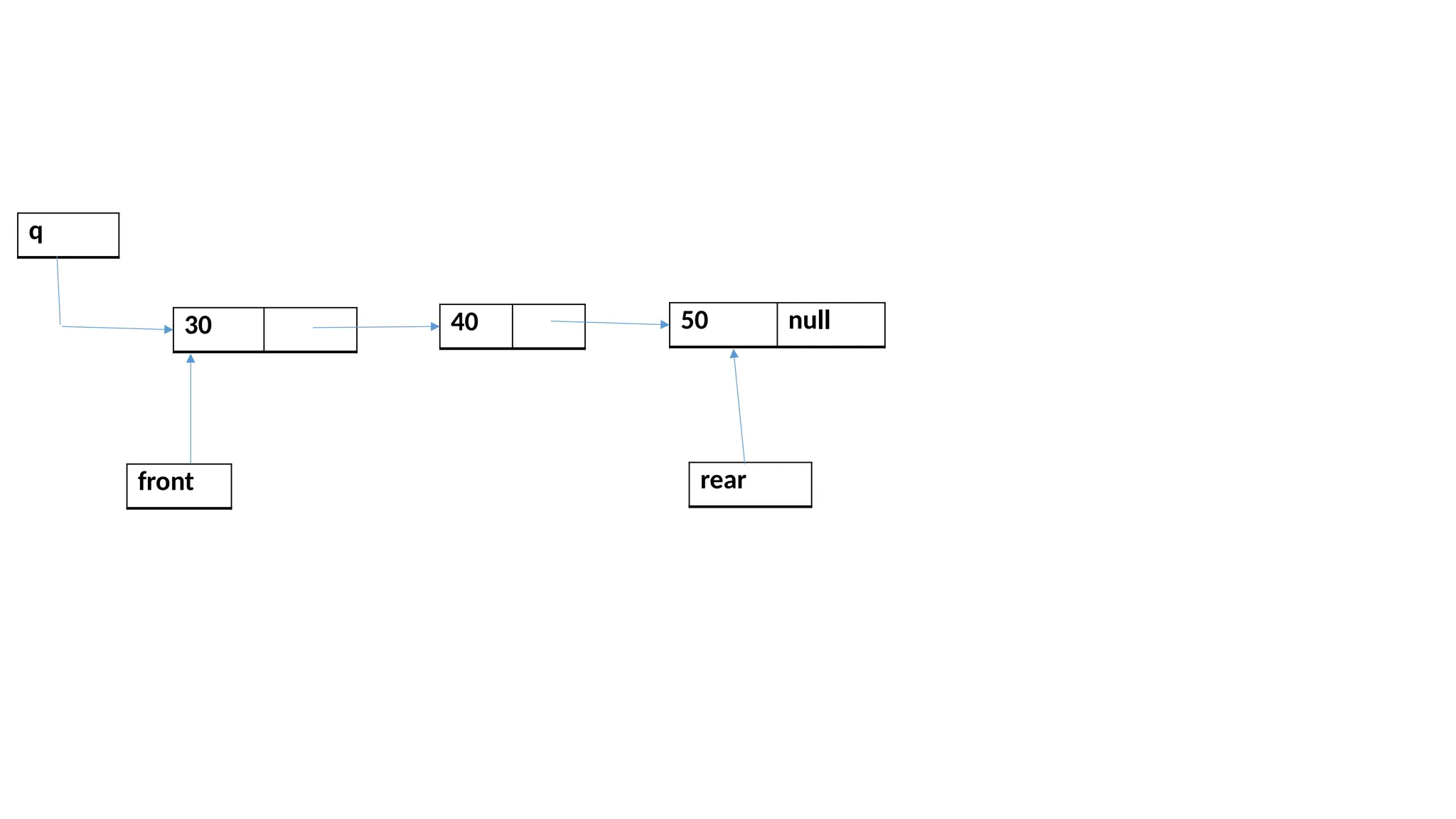
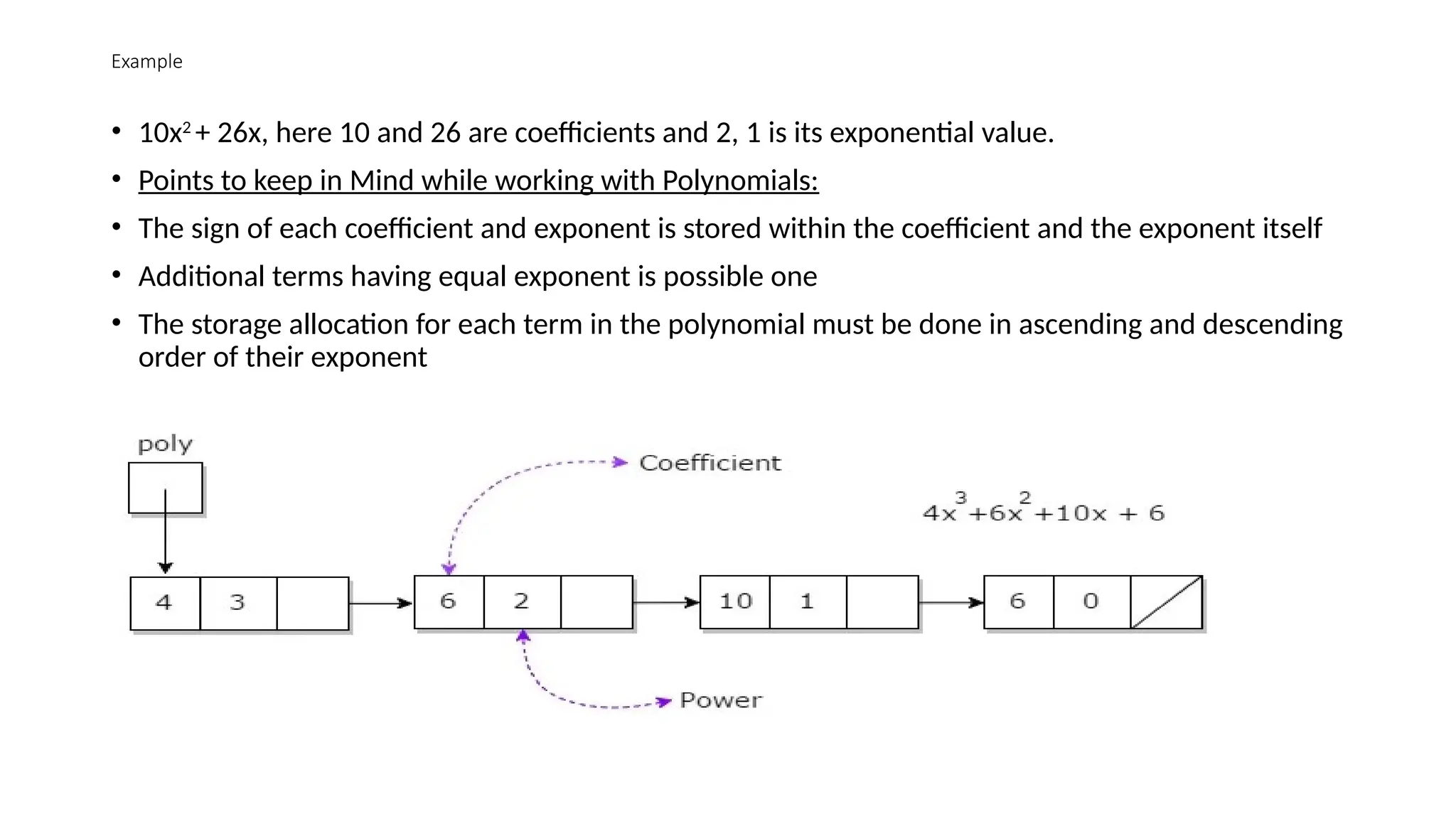
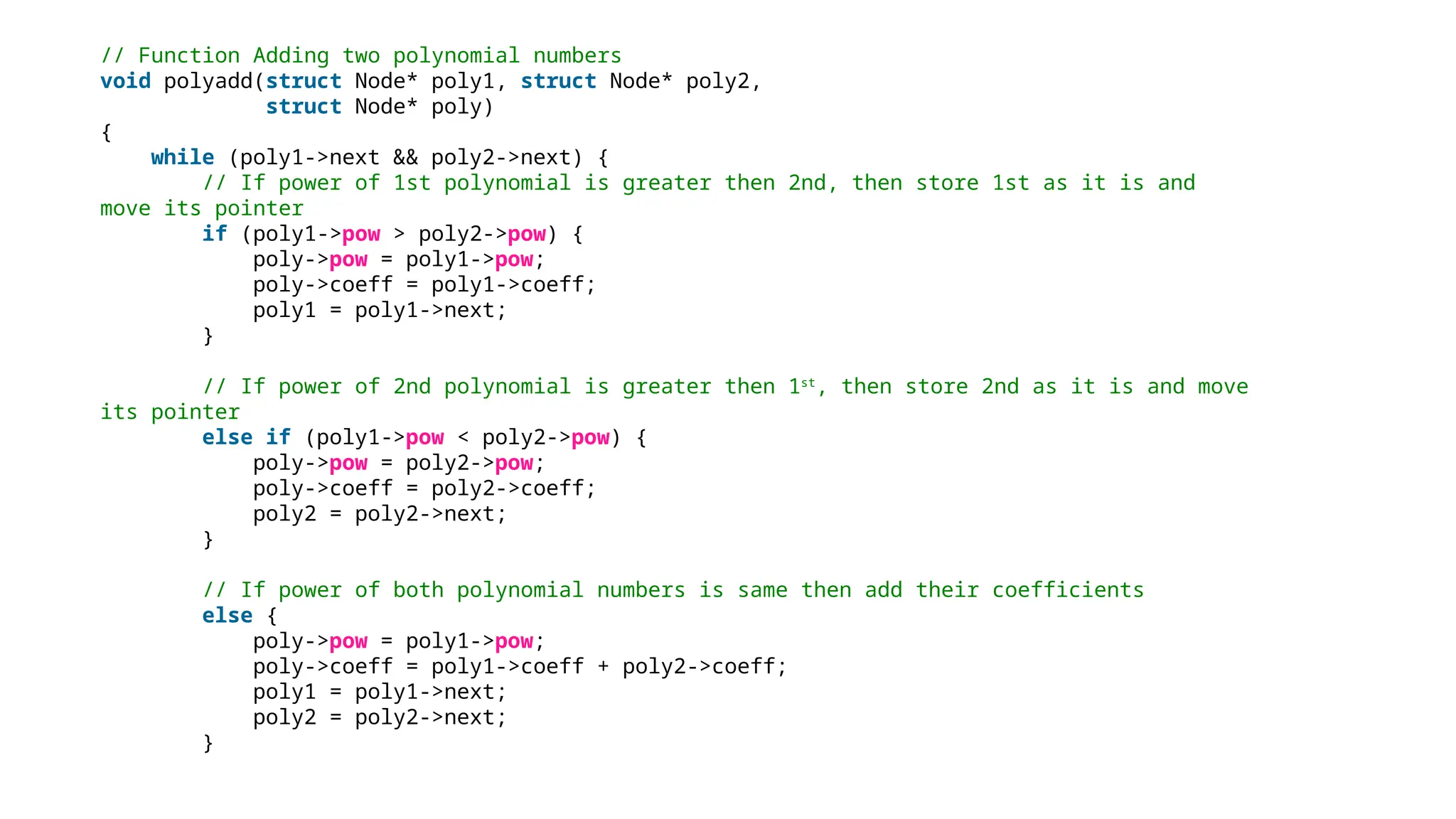
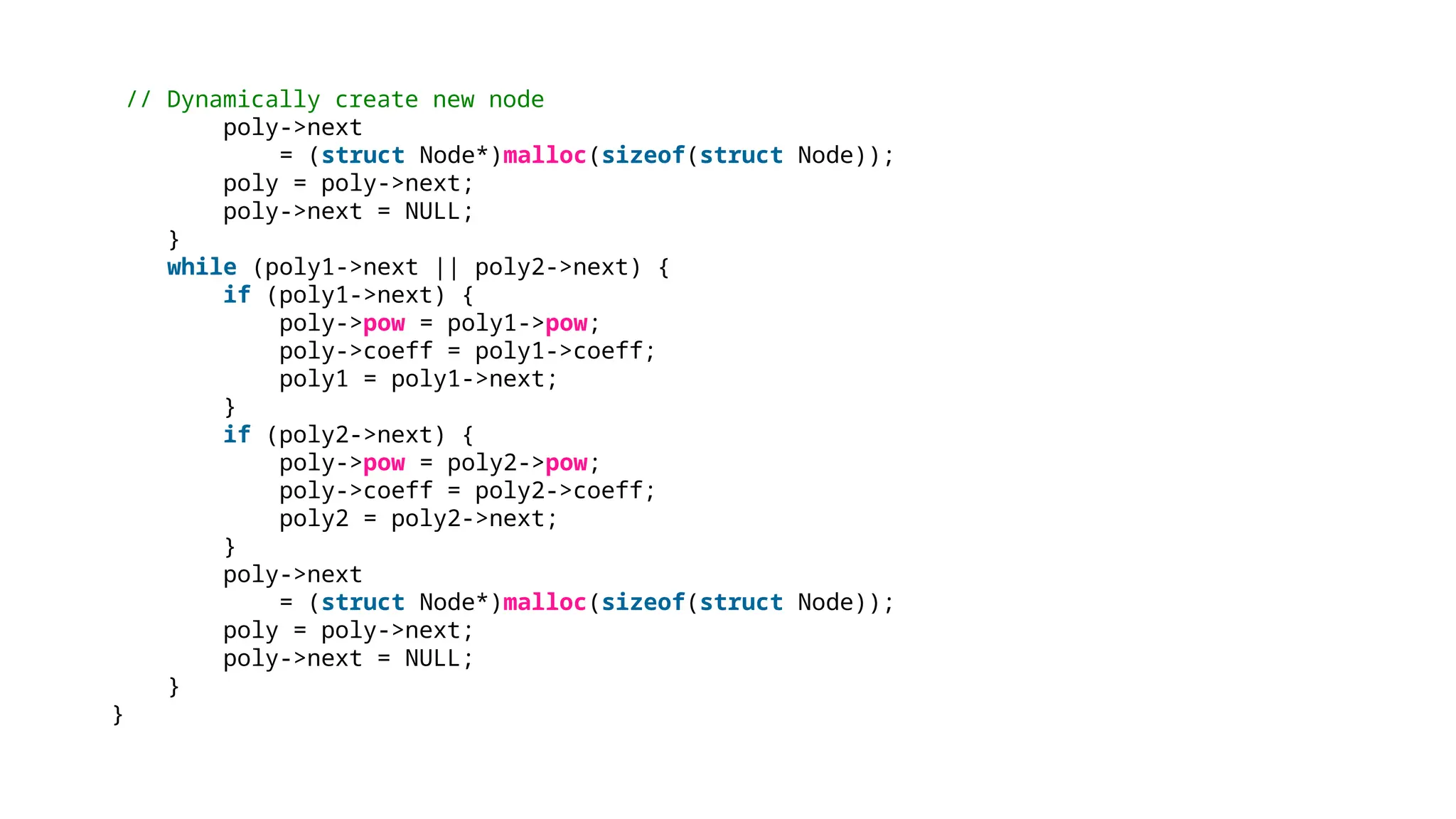
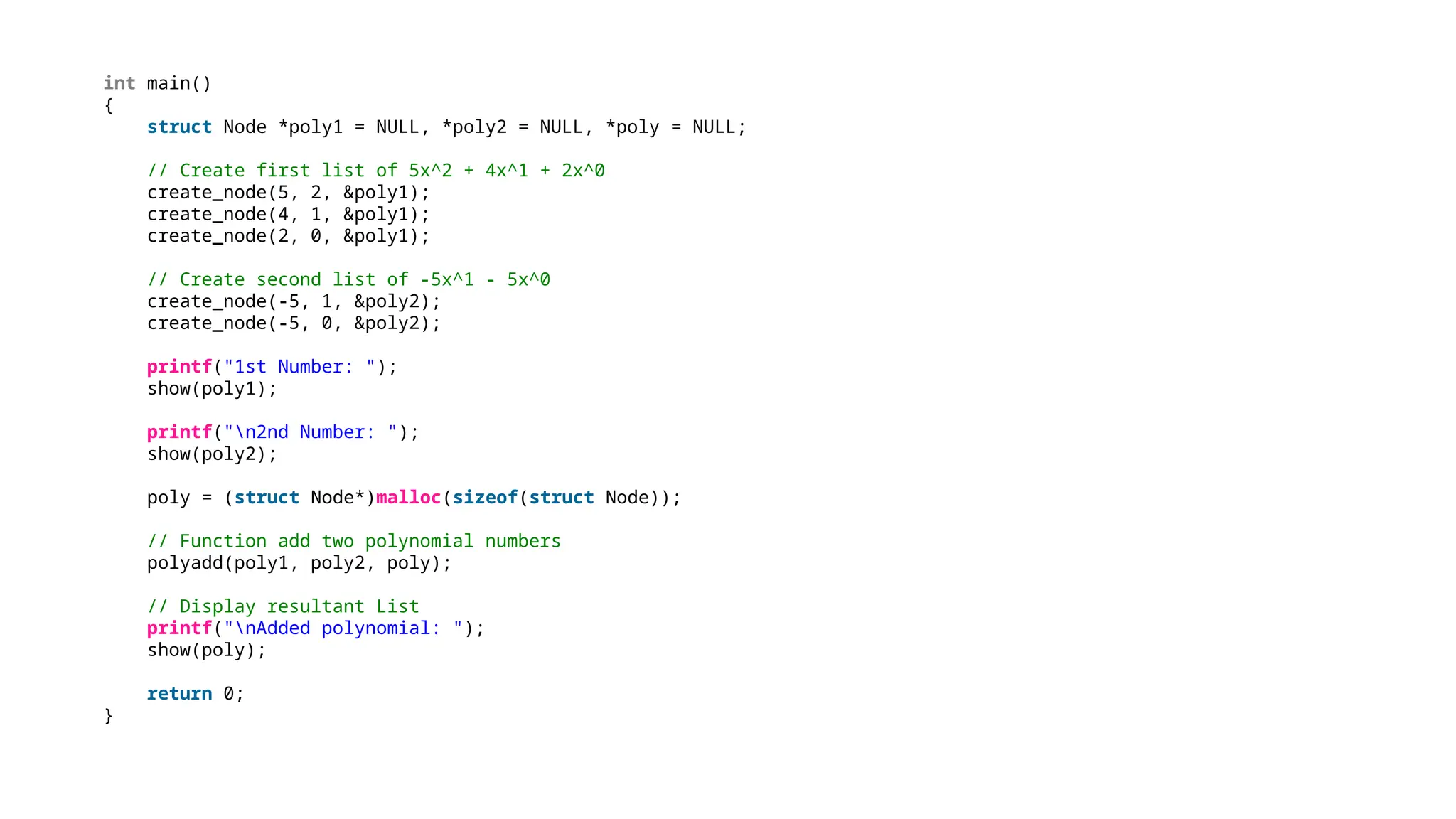
The document provides a detailed explanation of implementing data structures like stacks and queues using singly linked lists. It describes stack operations (push, pop, peek, display) and their efficiency, as well as queue operations (enqueue, dequeue) and their implementation, highlighting the advantages of linked lists over arrays. Additionally, it covers polynomial representation using linked lists, including the addition of two polynomials, showcasing the corresponding C programs for each structure.