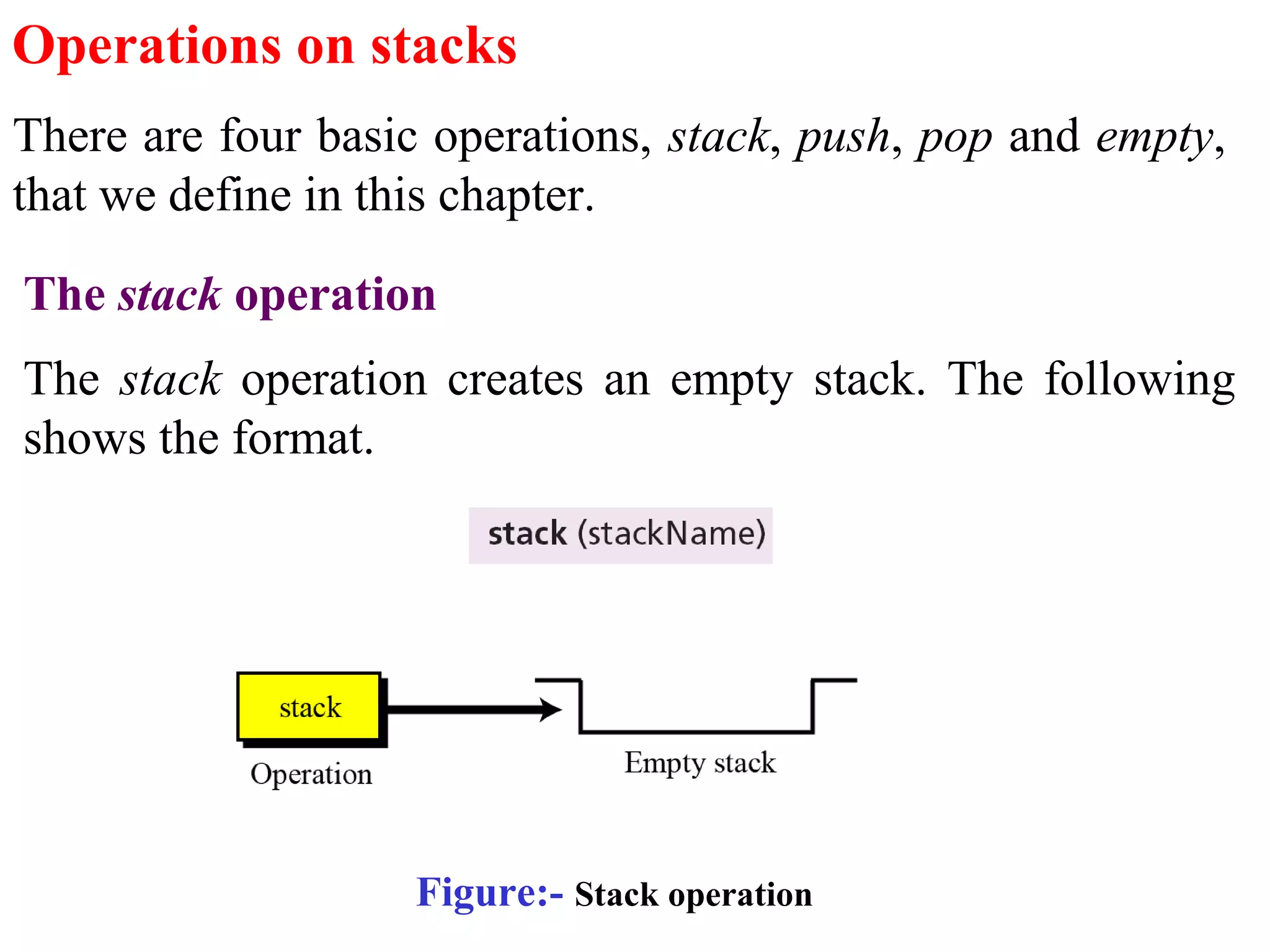
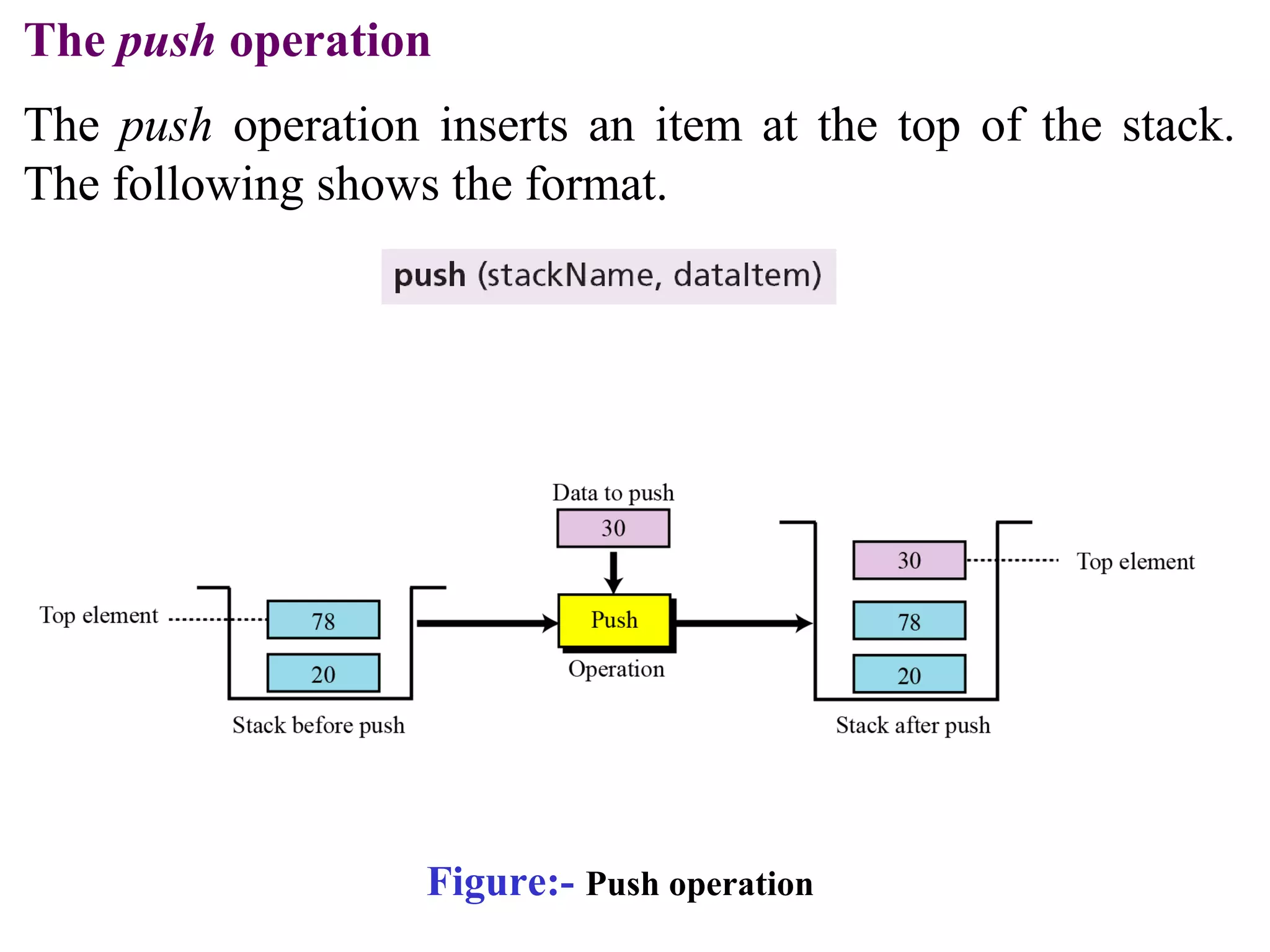
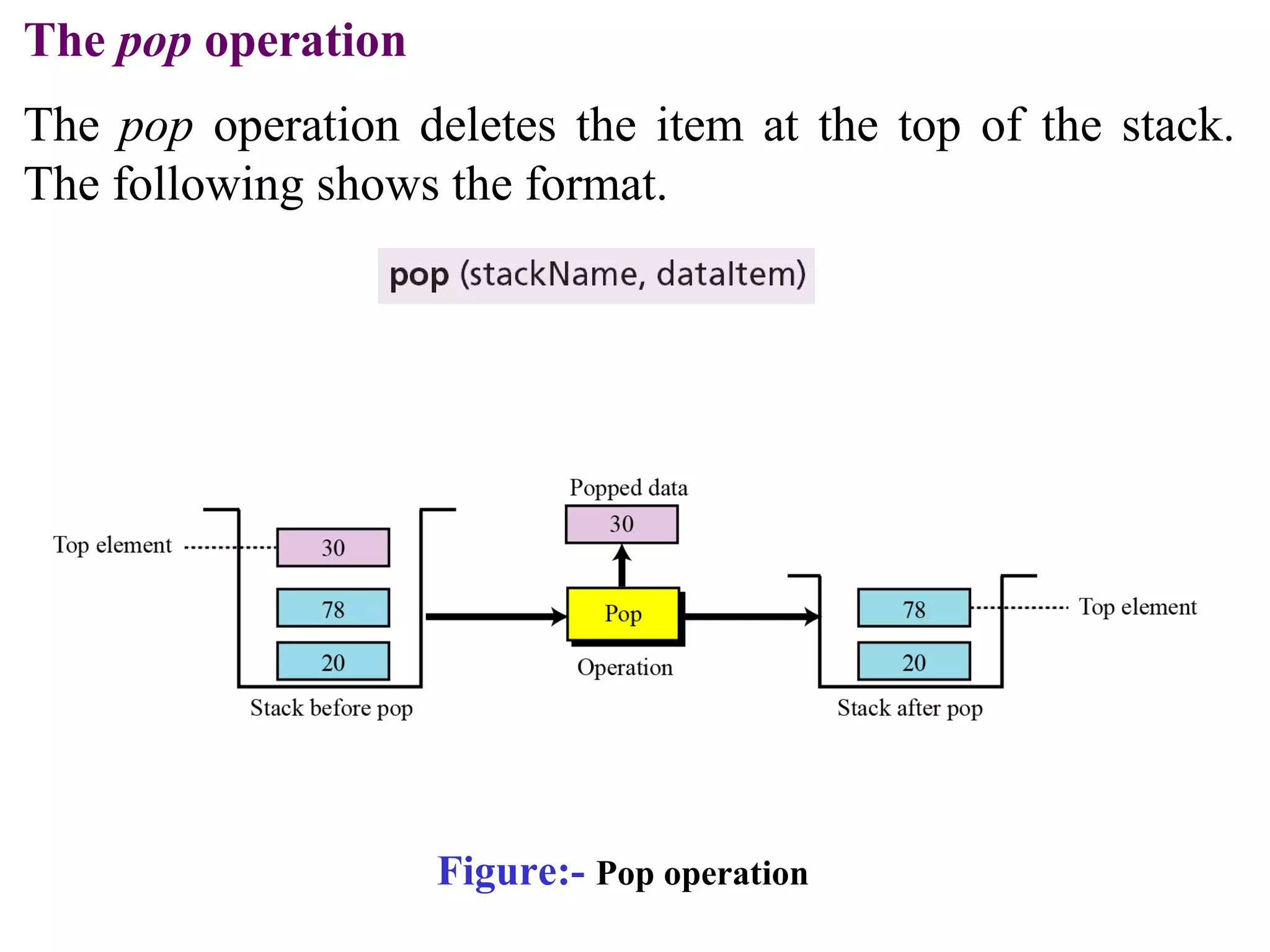
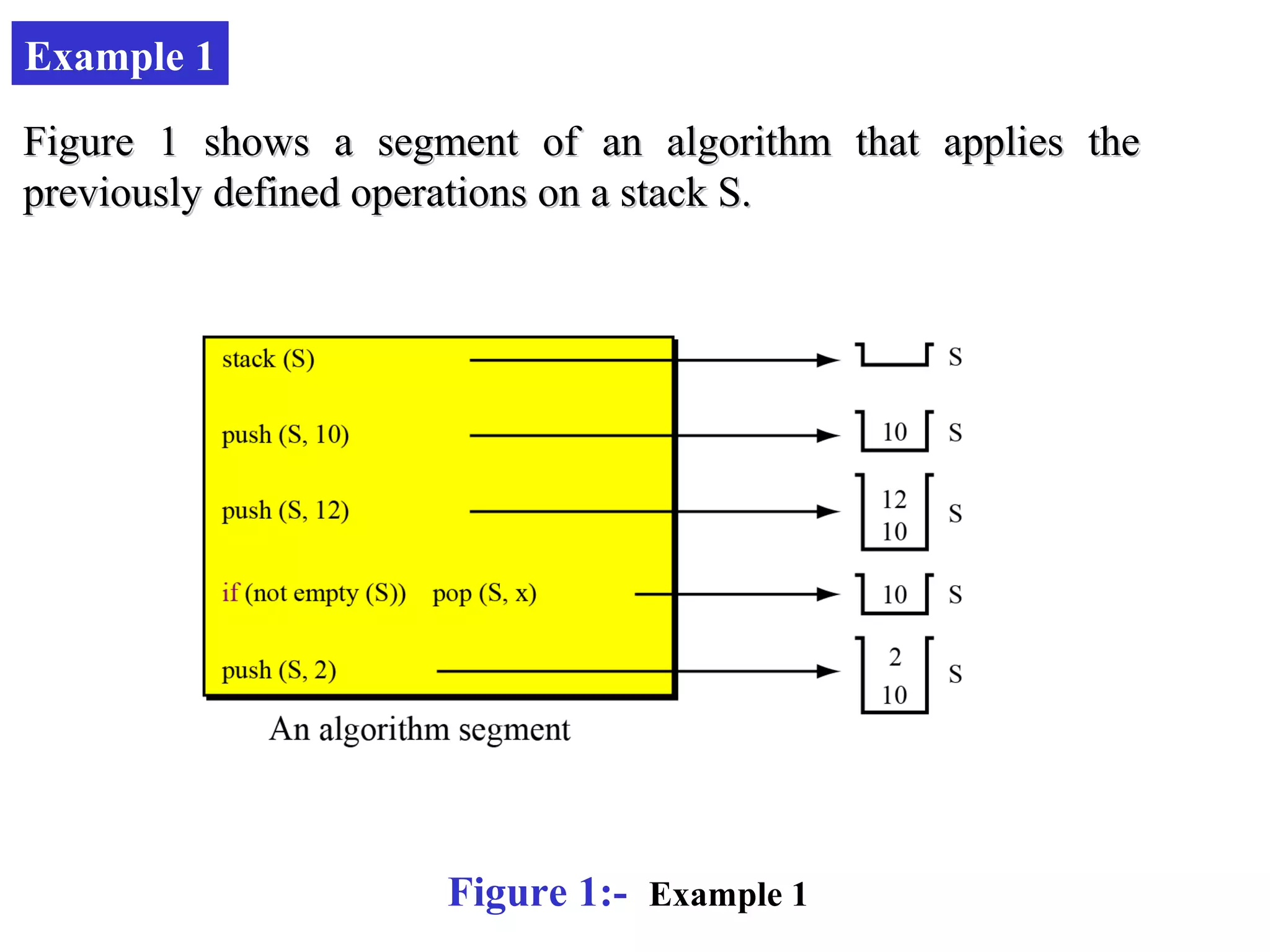
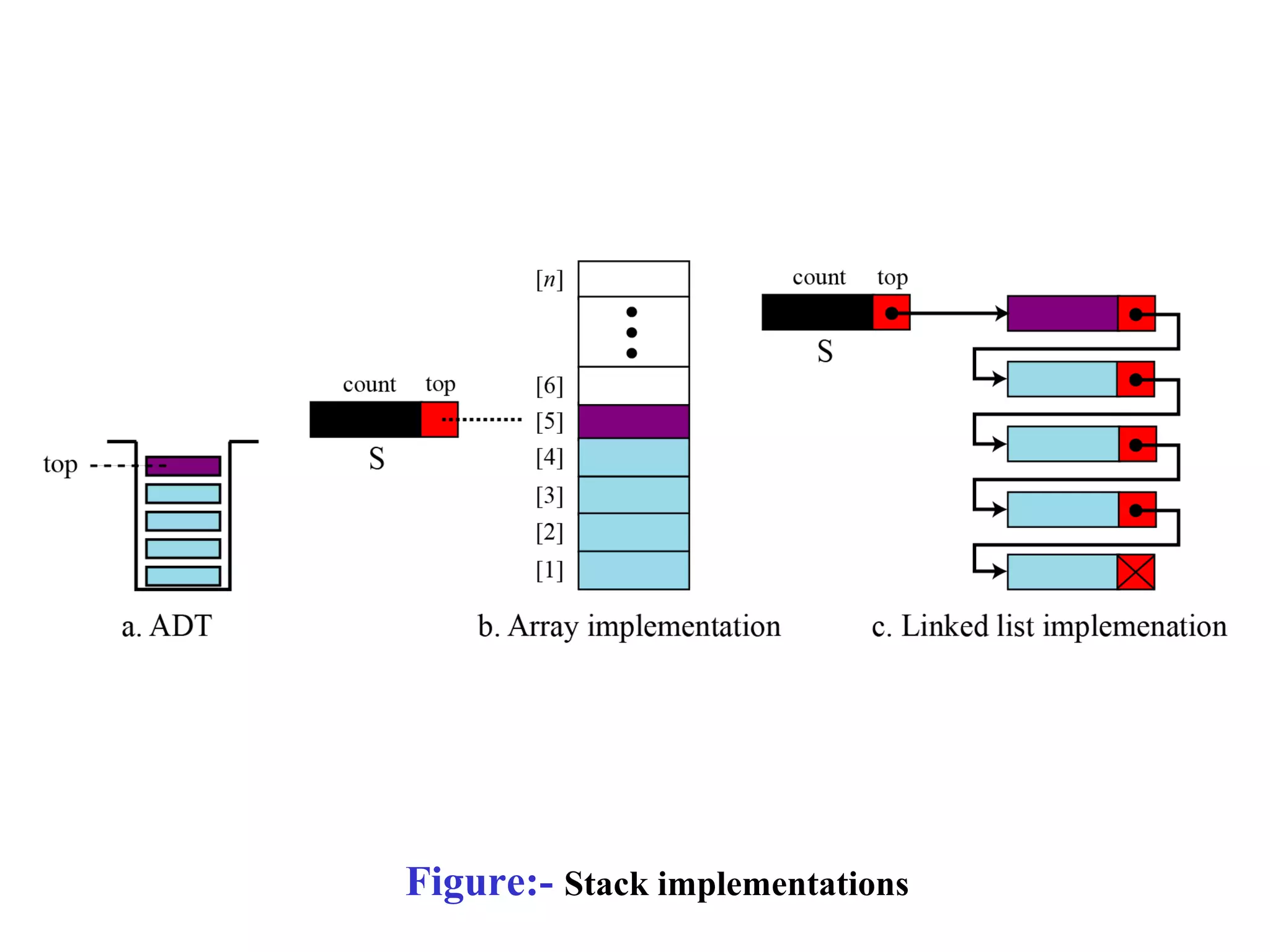
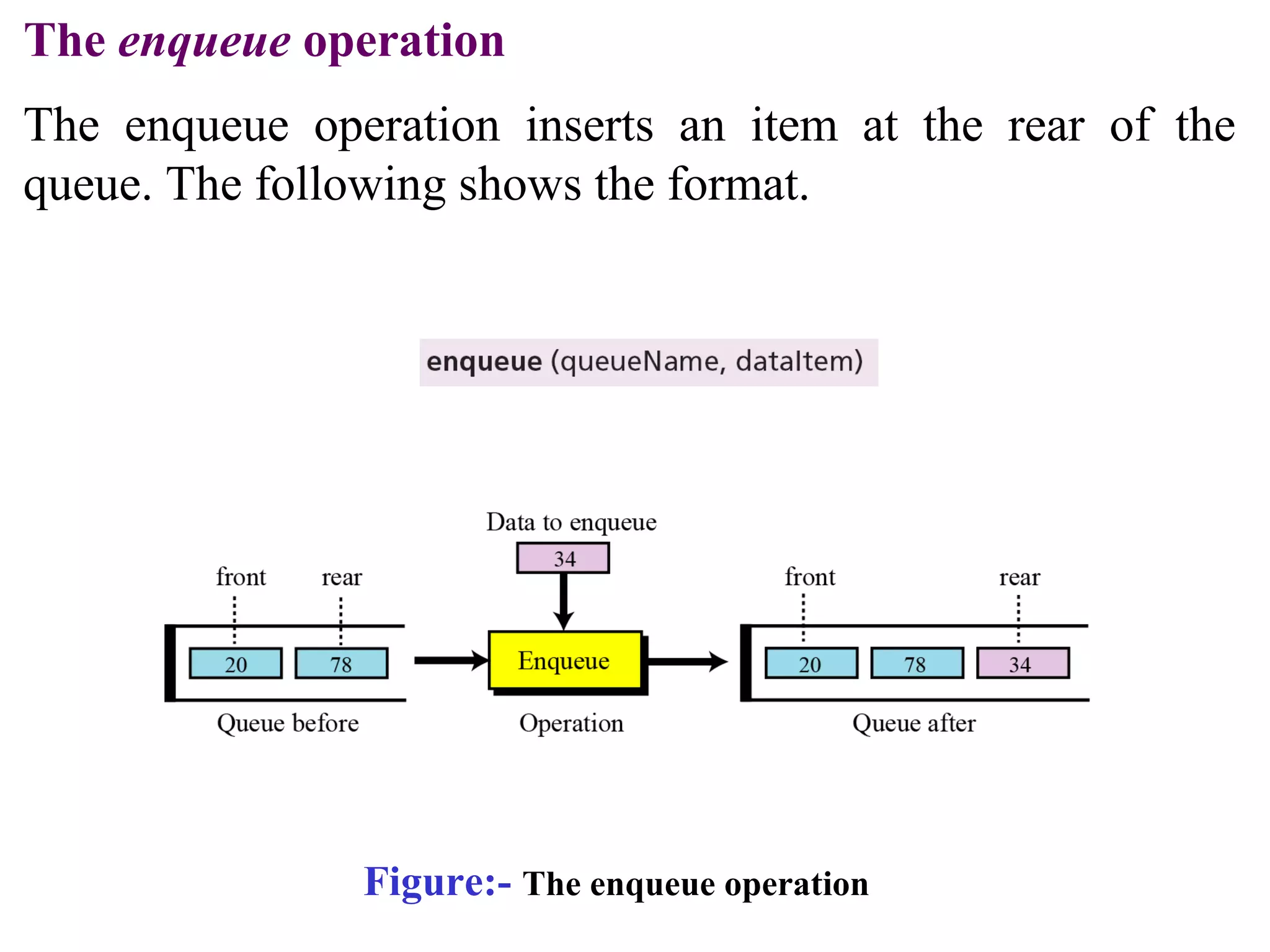
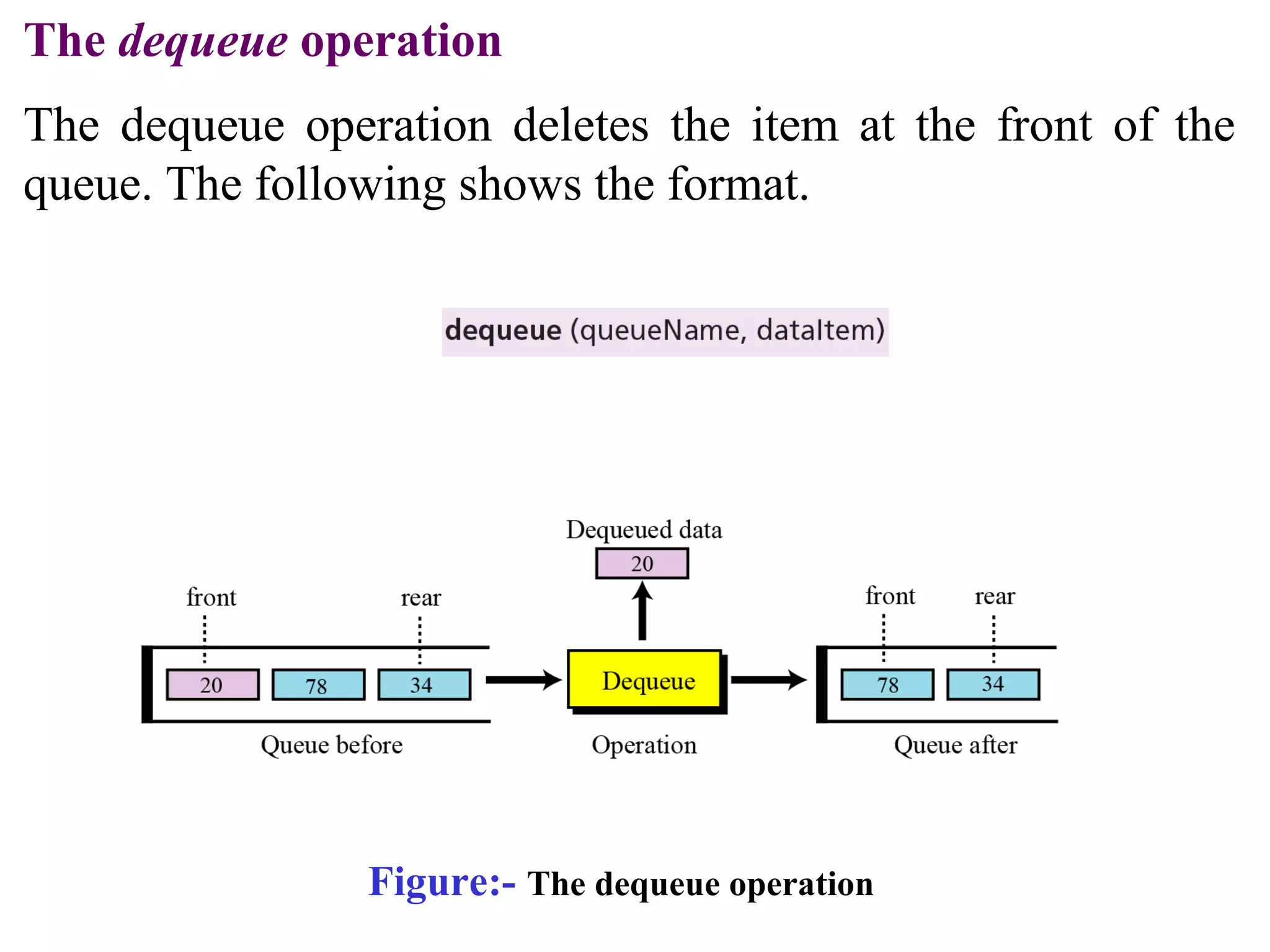
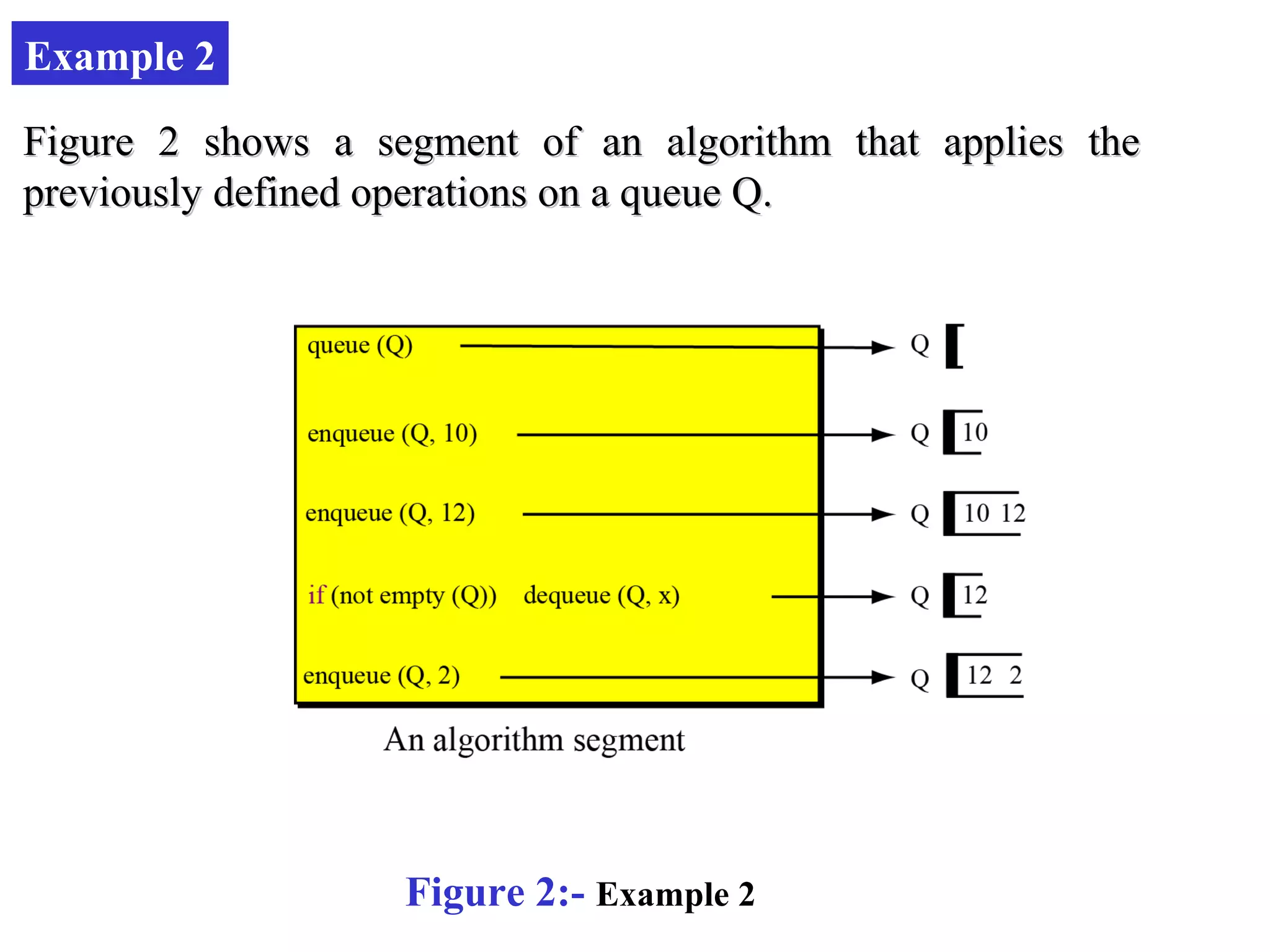
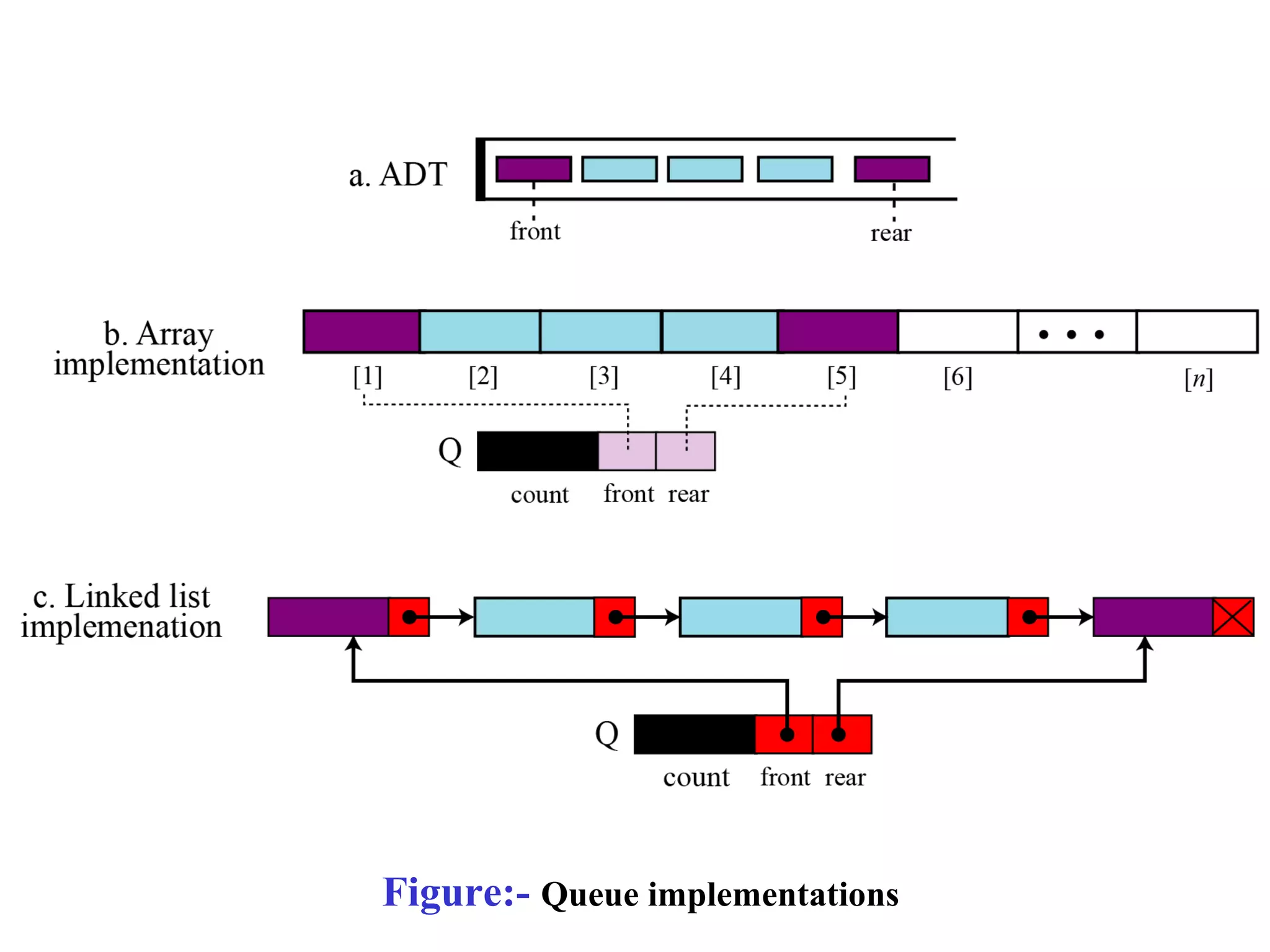
Stacks and queues are linear data structures. Stacks follow LIFO (last in, first out) where elements are added and removed from one end, while queues follow FIFO (first in, first out) where elements are added to one end and removed from the other. Both have basic operations like push/enqueue and pop/dequeue to add and remove elements. Stacks and queues can be implemented using arrays, linked lists, or other data structures.