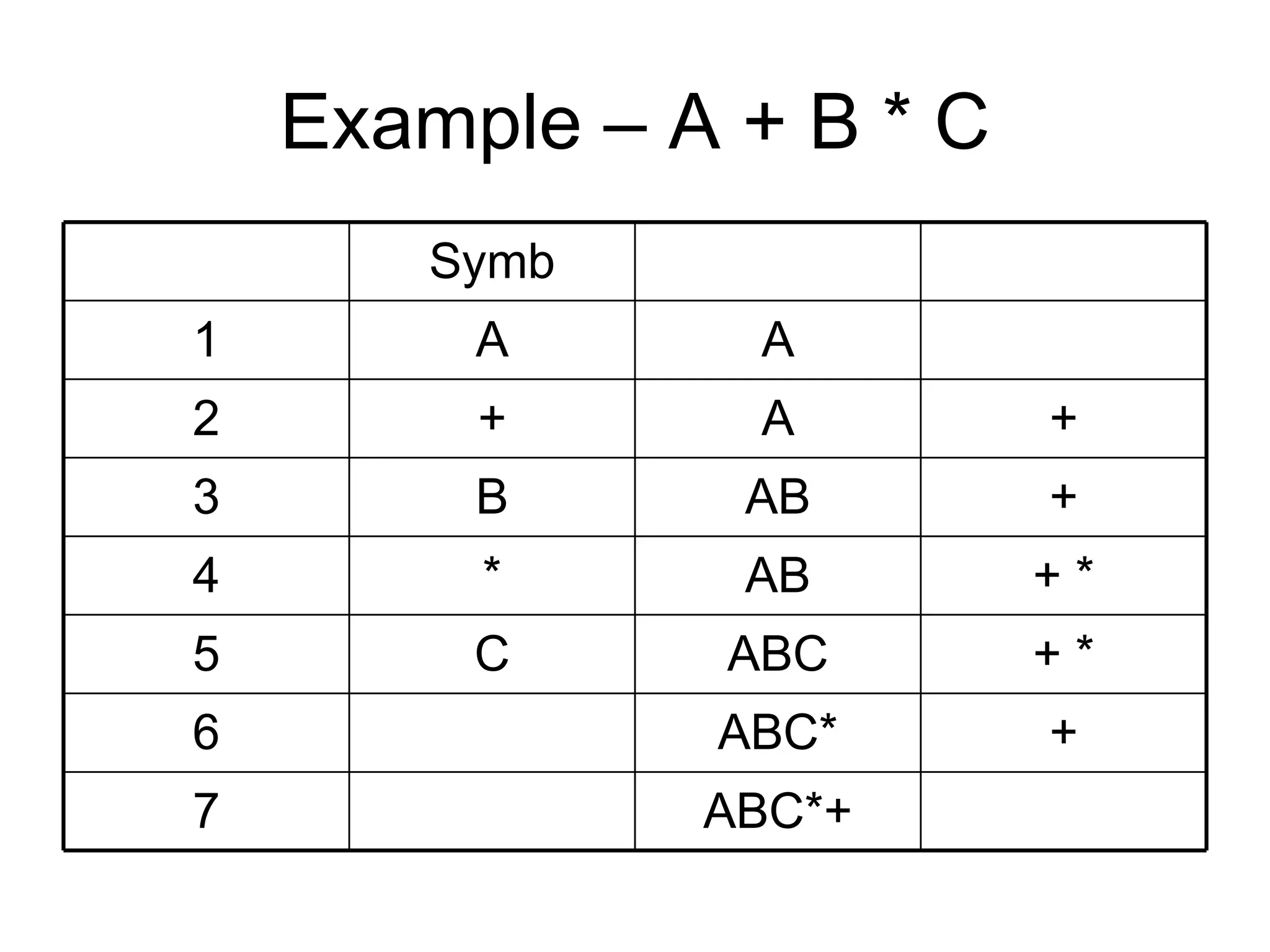
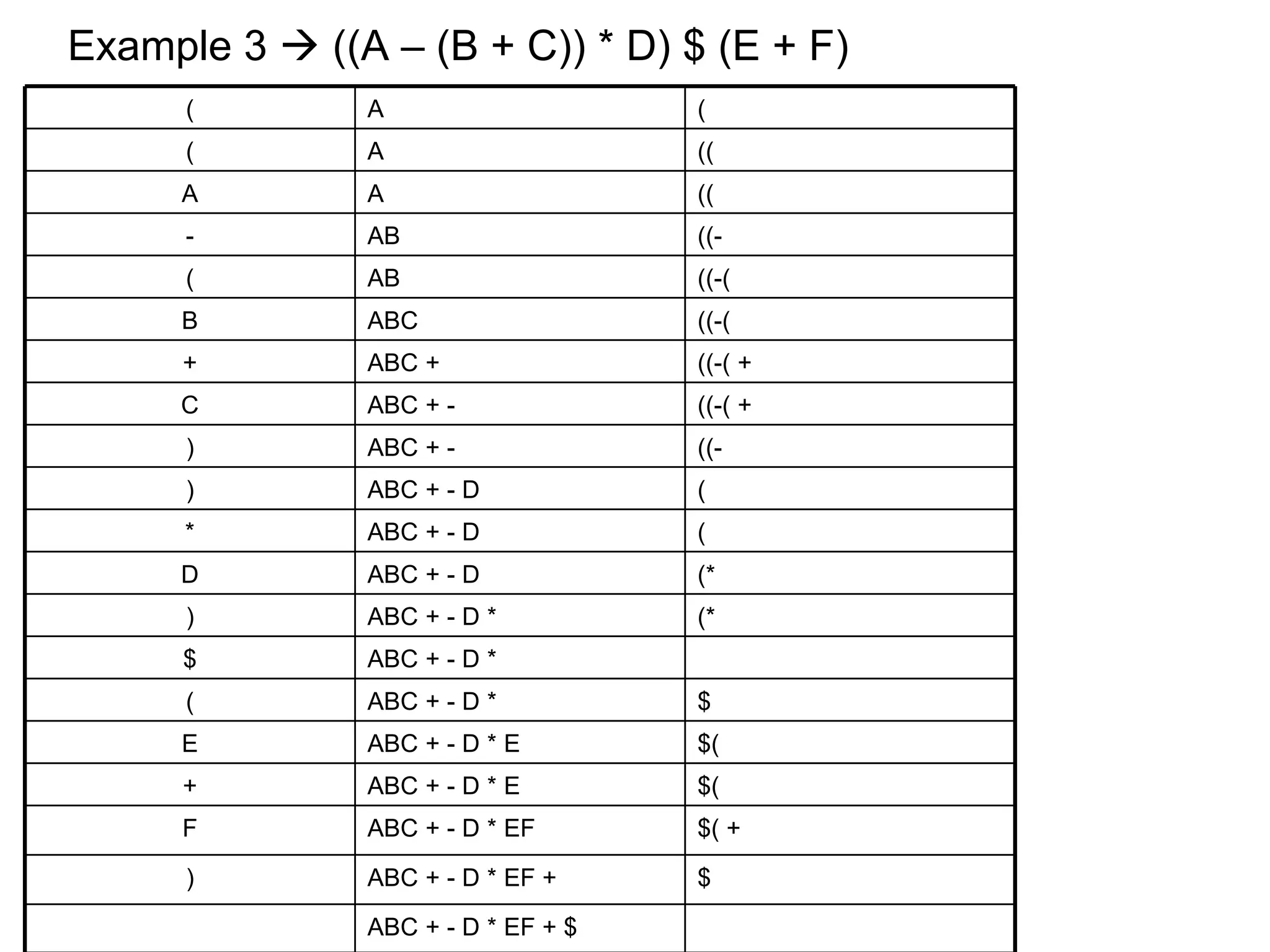
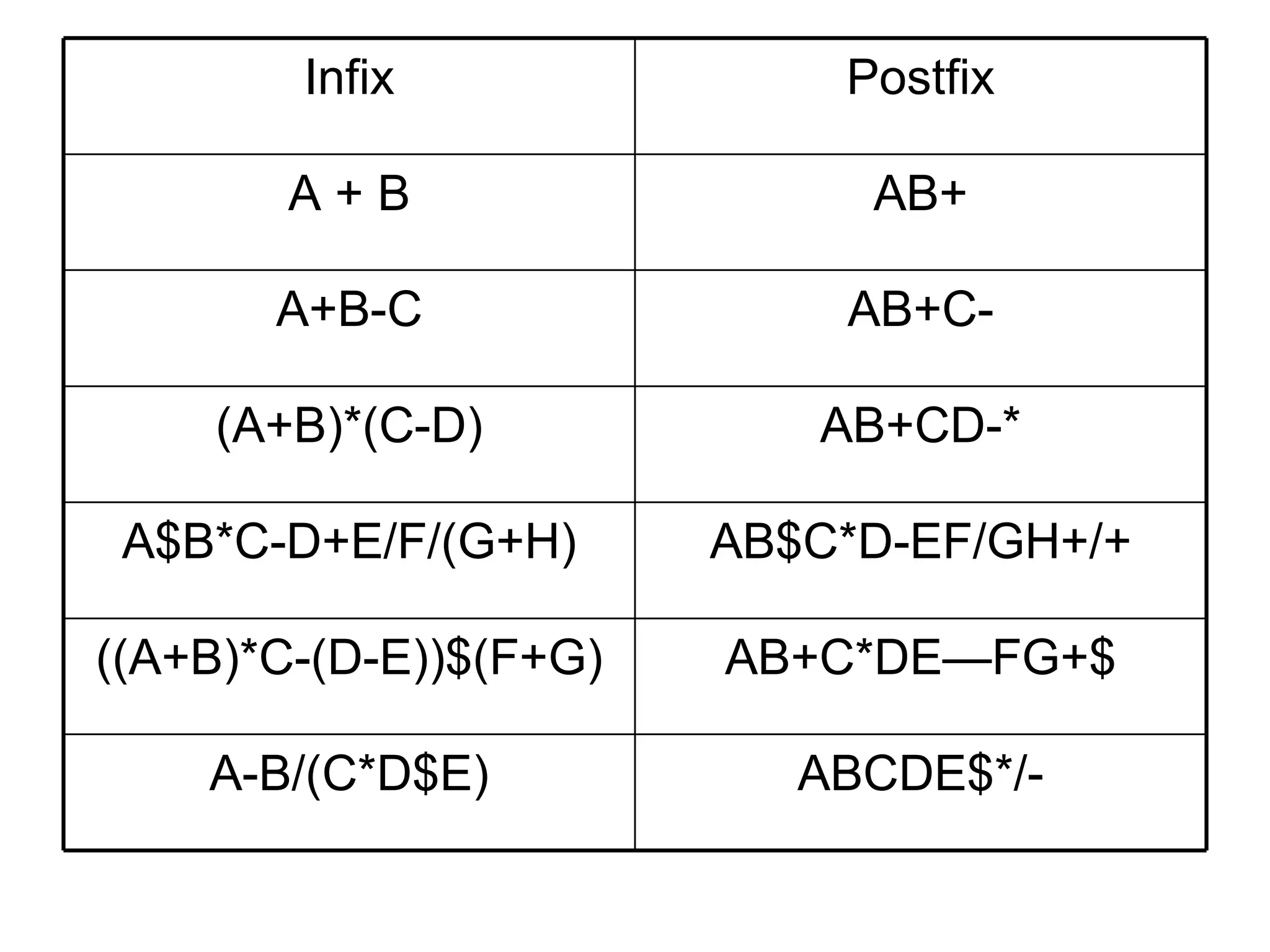
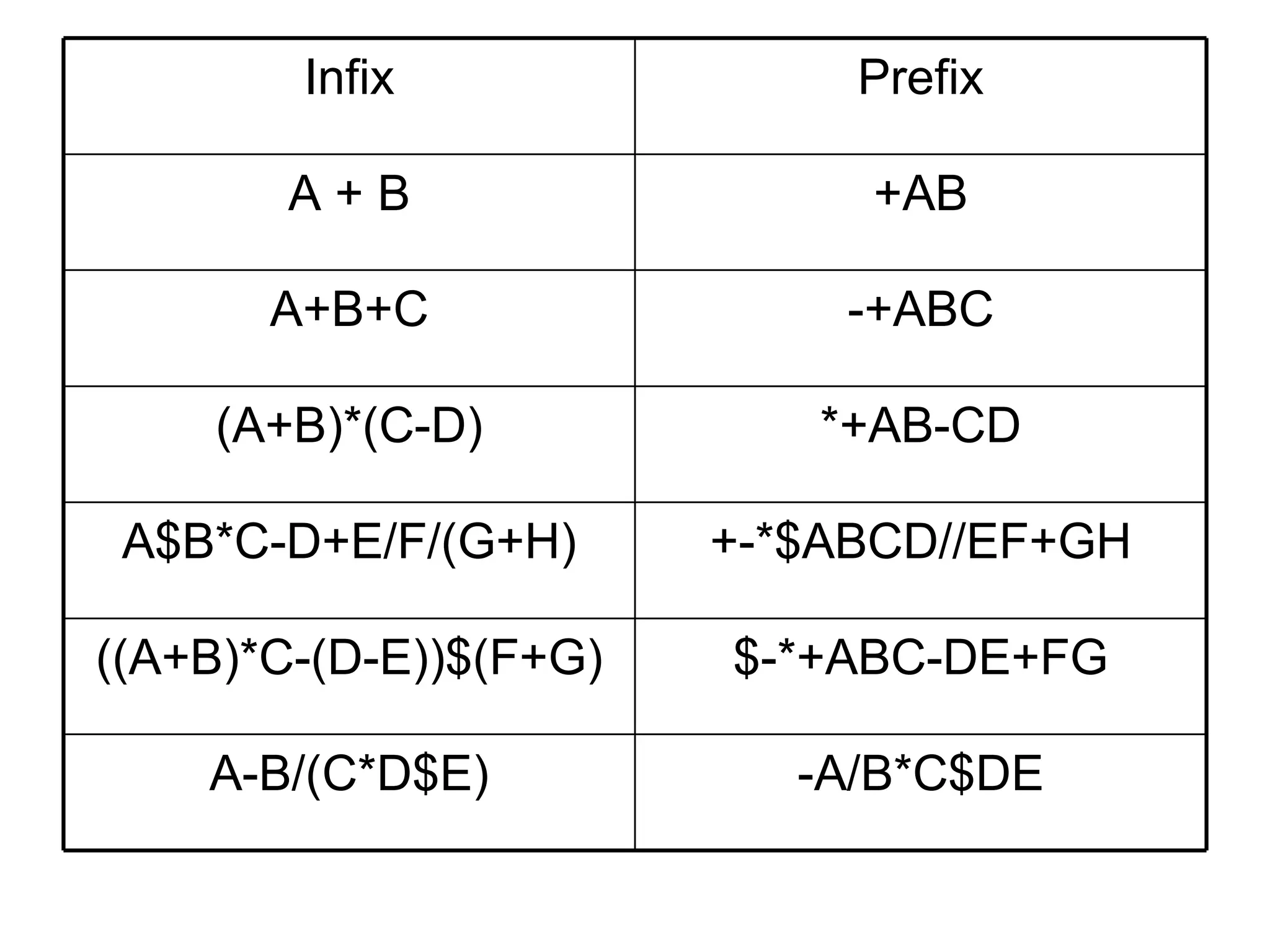
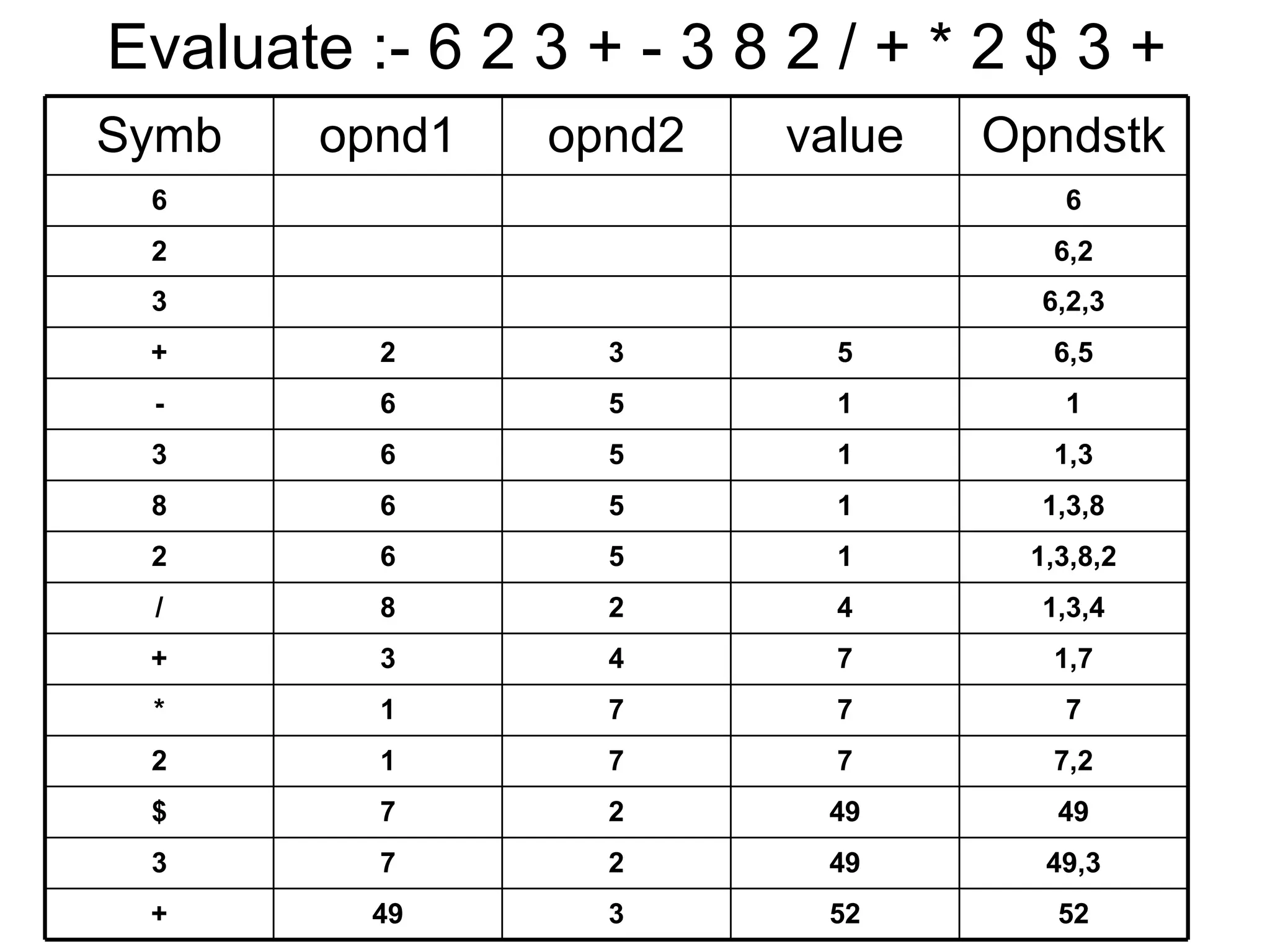
The document discusses infix, prefix and postfix notation for mathematical expressions. It provides examples of converting expressions between these notations. It also describes evaluating postfix expressions using a stack, and converting infix expressions to postfix using precedence rules.








![Circular Queue (Insertion) void insert(int val) { if((front==0 && rear==MAX-1) || (rear+1==front)) printf(" Circular Queue is Full"); else { if(rear==MAX-1) rear=0; else rear++; a[rear]=val; } if(front==-1) front=0; }](https://image.slidesharecdn.com/circularqueues-111024104135-phpapp02/75/Circular-queues-12-2048.jpg)
![55 44 33 22 11 22 11 55 44 11 55 44 33 22 4 3 2 1 0 1 0 4 3 0 4 3 2 1 Rear Front Front = 0 Rear = max – 1 Queue is full Rear Front Rear Front Front != 0 & Rear = max-1 Rear = 0 A[rear] = val 33 2 Front !=0 & Rear != max-1 Rear ++ A[rear] = val Inserting an element into queue (all conditions) Since if your queue is empty means (front=-1) then make front =0 & rear = 0 (by rear++) It will become 0 means(-1+1=0)](https://image.slidesharecdn.com/circularqueues-111024104135-phpapp02/75/Circular-queues-13-2048.jpg)
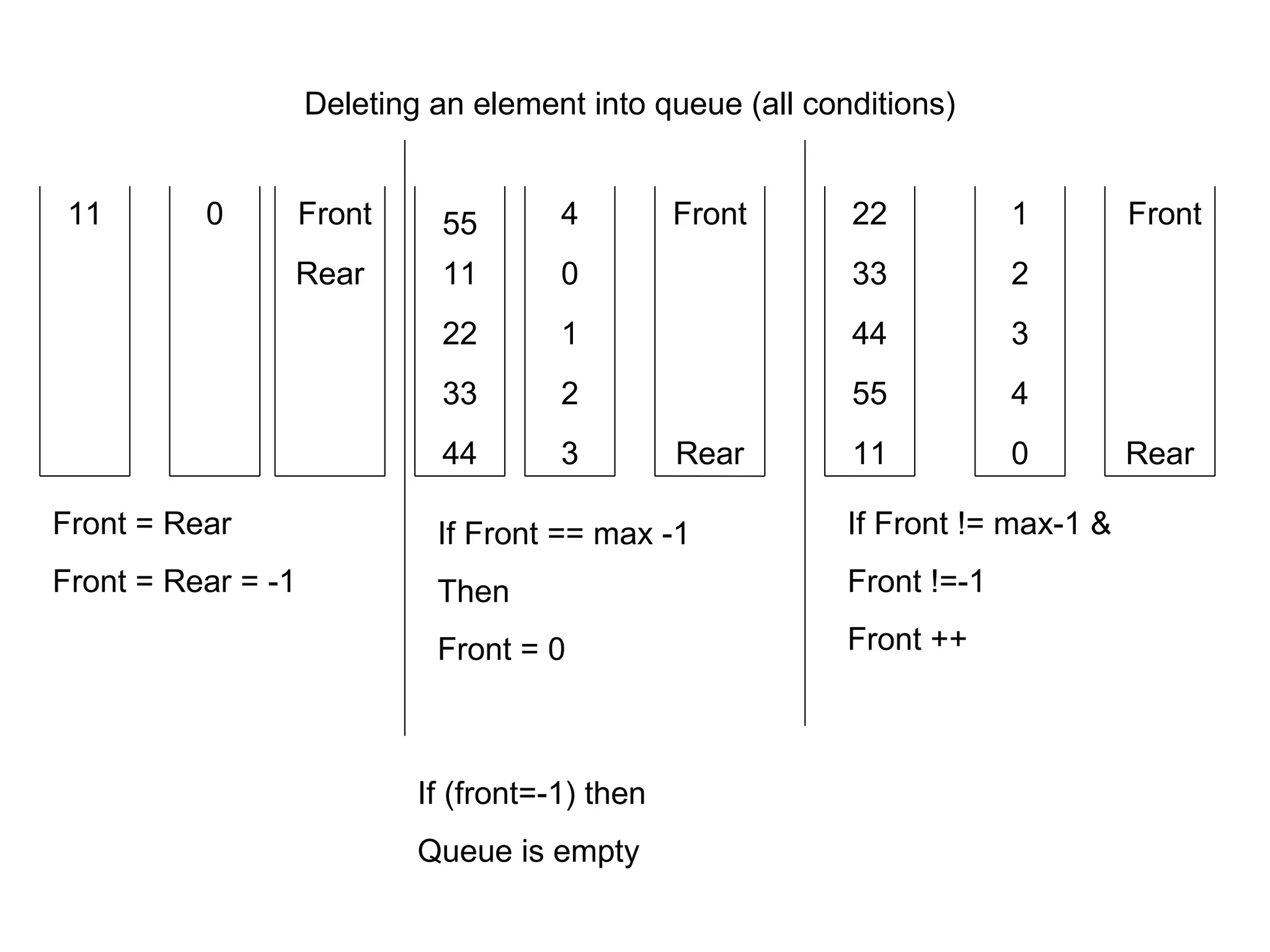
![Circular Queue (Deletion) int deletion() { int k; if(front==-1) printf("Circular Queue is Empty"); else { k=a[front]; if(front==rear) front=rear=-1; else { if(front==MAX-1) front=0; else front++; } } return k; }](https://image.slidesharecdn.com/circularqueues-111024104135-phpapp02/75/Circular-queues-14-2048.jpg)
![void display() { int i; if(front==-1) printf("Circular Queue is Empty"); else { if(rear < front) { for(i=front;i<=MAX-1;i++) printf("%d ",a[i]); for(i=0;i<=rear;i++) printf("%d ",a[i]); } else { for(i=front;i<=rear;i++) printf("%d \n ",a[i]); } } }](https://image.slidesharecdn.com/circularqueues-111024104135-phpapp02/75/Circular-queues-16-2048.jpg)