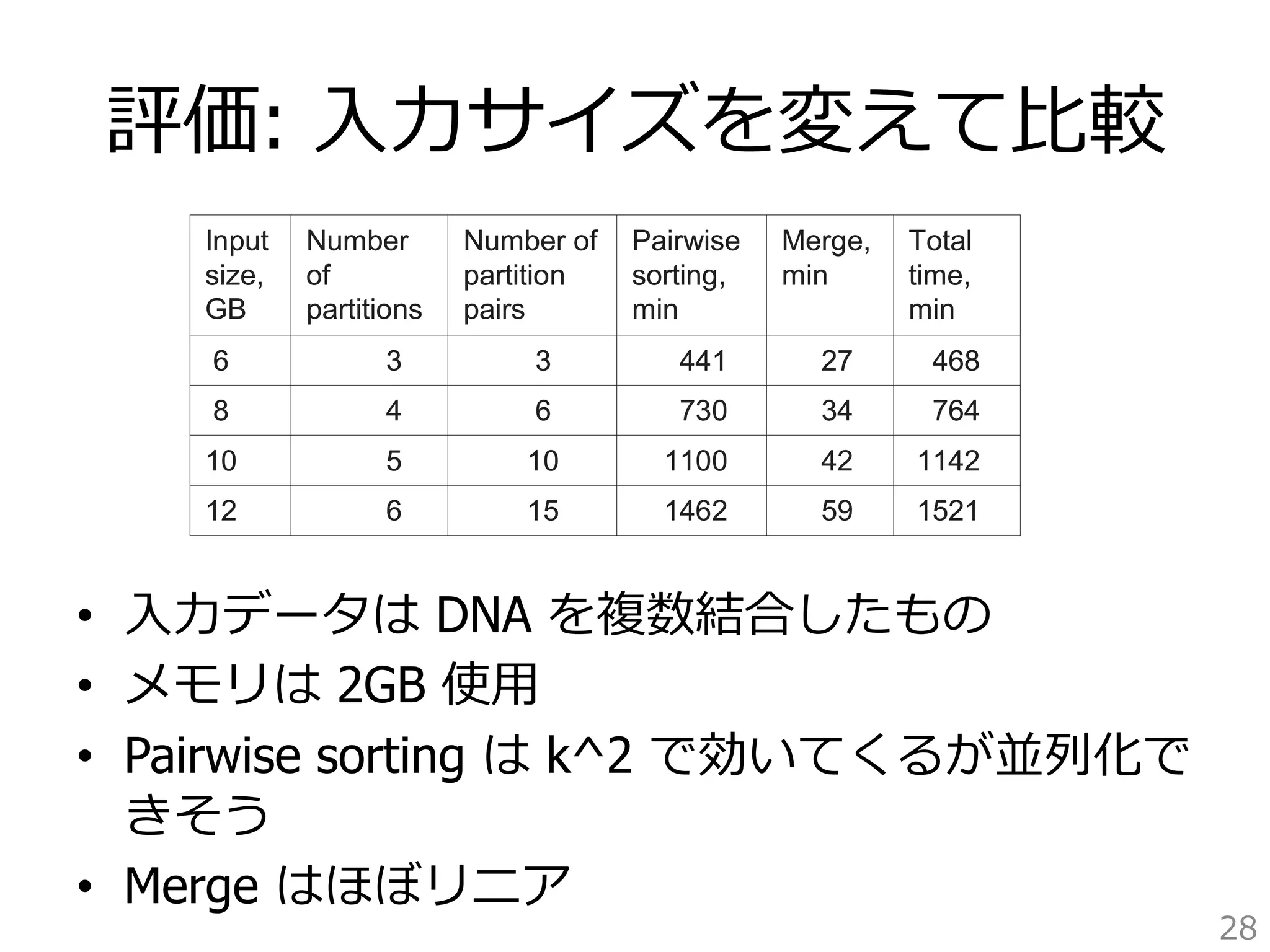
The document introduces an algorithm called B2ST (Big tree, Big string Suffix Tree construction) for constructing suffix trees of data larger than main memory. B2ST partitions the input string into partitions that fit in memory, sorts suffixes within partition pairs using suffix arrays with LCP information, and merges the results by building a suffix tree from the suffix array streams and order arrays on disk in a single pass without reloading the entire input.




![変数の意味
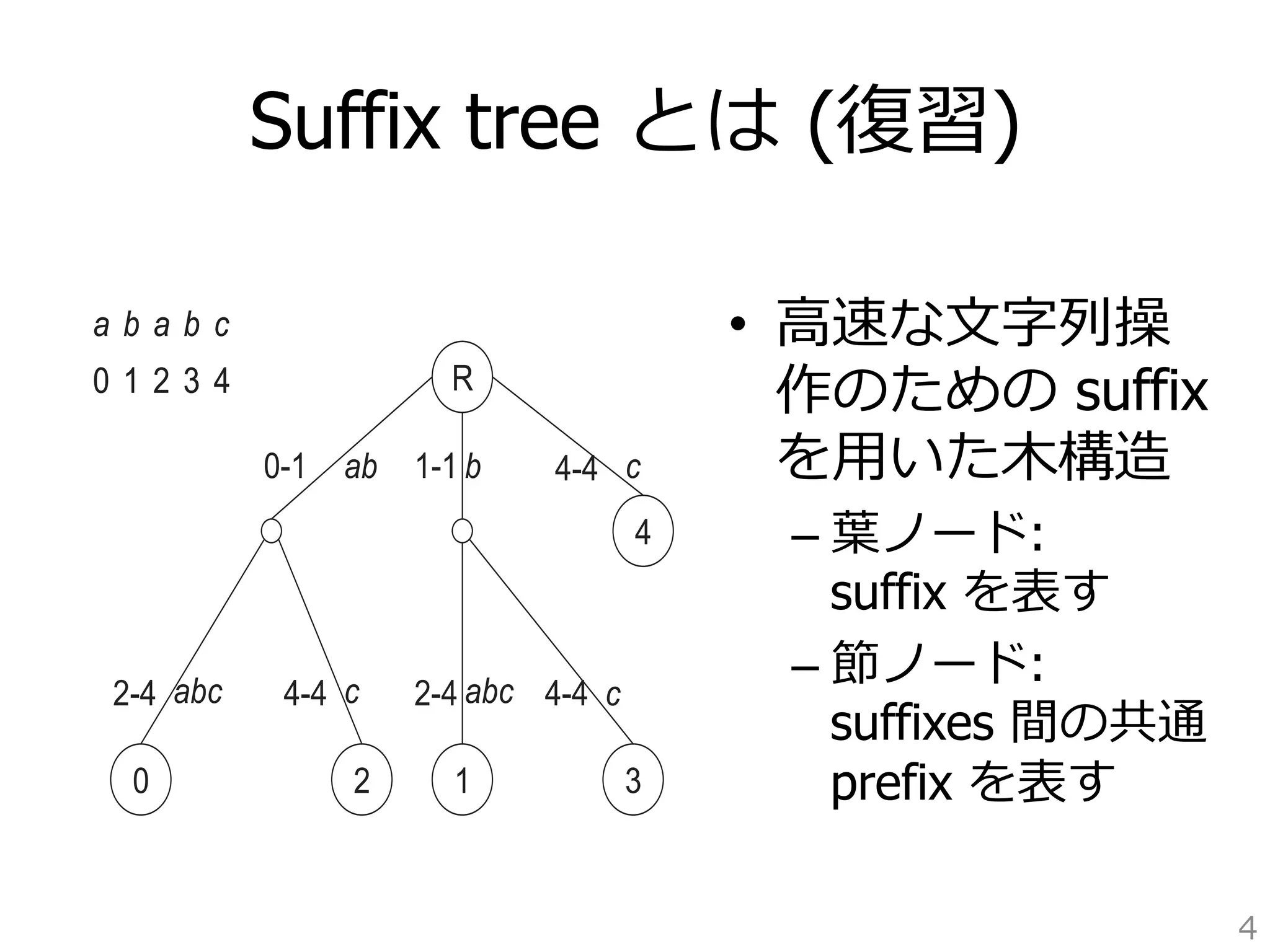
• X: ⼊入⼒力力⽂文字列列 (⻑⾧長さN)
• Xij: X[i]からX[j-1]までの部分⽂文字列列
• Si: i 番⽬目の suffix (0 = i N)
• LCPij: Si と Sj の longest common prefix
• |LCPij|: LCPij の⻑⾧長さ
• SA: suffix array
• ST: suffix tree
6](https://image.slidesharecdn.com/suffix-tree-over-memory-140828232352-phpapp02/75/Sufix-Array-6-2048.jpg)




![5. Merge algorithm
13
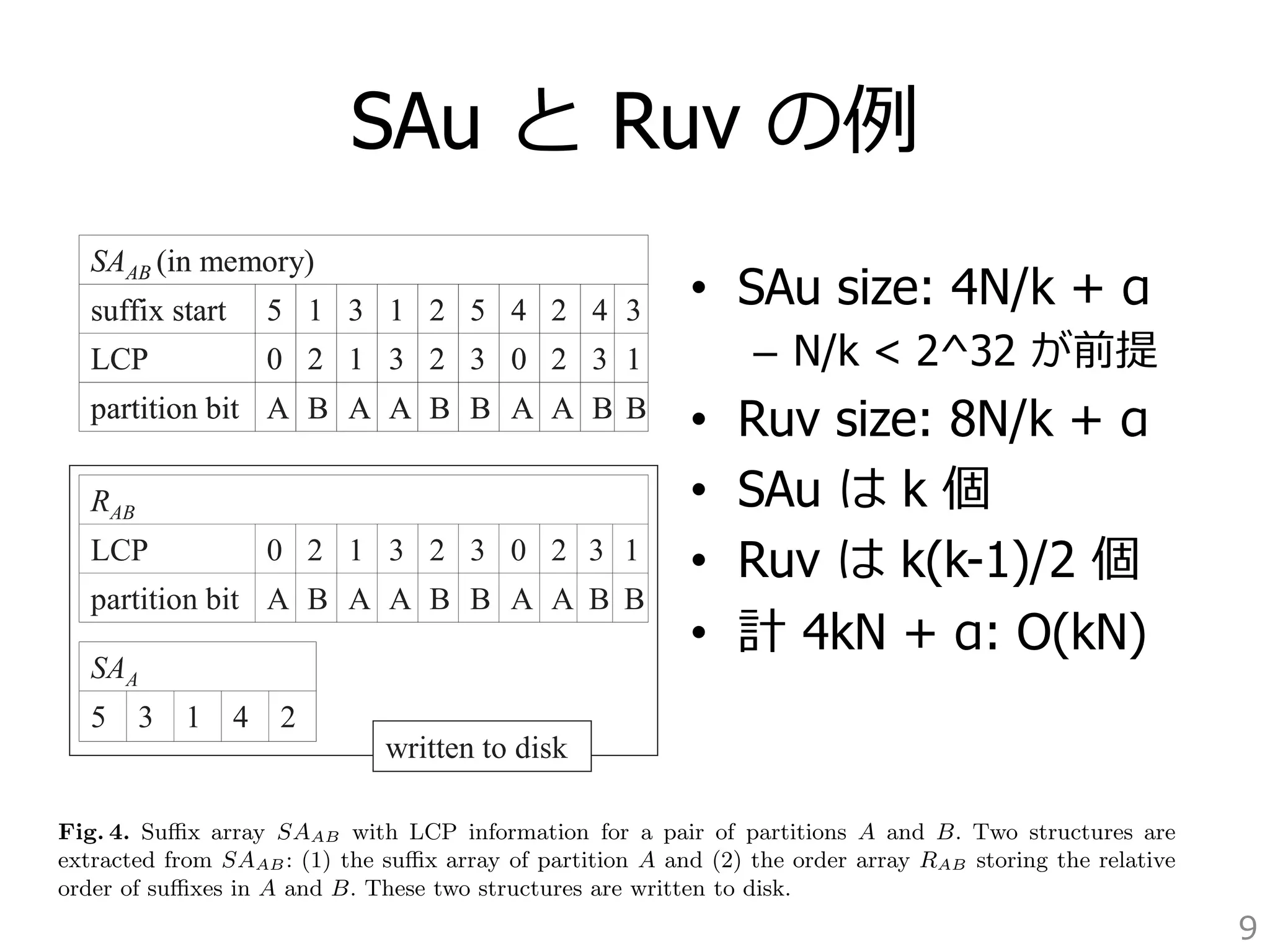
What happens with each suffix in the output buffer is the subject pseudocode of merge is shown in Figure 8.
Algorithm merge
1. lastTransferred = null
2. while heap is not empty
3. remove smallest suffix Si of partition u
from the top of the heap
4. rebalance heap
5. lcp = 0
6. if lastTransferred is not null
7. v = lastTransferred.partitionID
8. lcp = LCP from R_bufuv [current_pointer]
9. create leaf for Si using lcp in ST_buf
10. advancePointers (u)
11. lastTransferred=Si
12. if ST_buf is full
13. store Si (max suffix)
as a pointer to the current tree
14. write ST_buf to disk
4. rebalance heap
5. lcp = 0
6. if lastTransferred is not null
7. v = lastTransferred.partitionID
8. lcp = LCP from R_bufuv [current_pointer]
9. create leaf for Si using lcp in ST_buf
10. advancePointers (u)
11. lastTransferred=Si
12. if ST_buf is full
13. store Si (max suffix)
as a pointer to the current tree
14. write ST_buf to disk
15. lastTransferred = null
16. Sj = get next suffix from SA_bufu
17. if Sj is not null
18. insert Sj into heap
Fig. 8. The general pseudocode for merge.
lcp = 0
6. if lastTransferred is not null
7. v = lastTransferred.partitionID
8. lcp = LCP from R_bufuv [current_pointer]
9. create leaf for Si using lcp in ST_buf
10. advancePointers (u)
11. lastTransferred=Si
12. if ST_buf is full
13. store Si (max suffix)
as a pointer to the current tree
14. write ST_buf to disk
15. lastTransferred = null
16. Sj = get next suffix from SA_bufu
17. if Sj is not null
18. insert Sj into heap
Fig. 8. The general pseudocode for merge.](https://image.slidesharecdn.com/suffix-tree-over-memory-140828232352-phpapp02/75/Sufix-Array-13-2048.jpg)
![the information we need to efficiently perform the merge. As produce information. Since each Ruv contains an information only about two partitions, we need to the use suffix one bit to tree represent for the the partition entire ID input in Ruv. string Specifically, X. we We use are 0 for doing u entire v (input u v). Figure string InitialMerge 4 shows into SAA main and memory. RAB extracted algorithmIn from fact, SAAB we for never At the end of this step we have on disk suffix arrays for partitions
partition access pair (k k (of total size plus k(k − 1)/2 order arrays for each possible pair of partitions (of total size kN).
Algorithm initializeMerge
This is all the information we need to efficiently perform the merge. As a result of merge we produce the suffix tree for the entire input string X. We are doing this without
loading the entire input string into main memory. In fact, we never access X anymore.
14
1. for each SA_bufu
2. read first m start positions
from disk suffix array SAu
Algorithm initializeMerge
1. for each SA_bufu
2. read first m start positions
3. for each R_bufuv
4. read first m/k LCP+partitionBit from Ruv
from disk suffix array SAu
3. for each R_bufuv
4. read first m/k LCP+partitionBit from Ruv
5. for each SA_bufu
6. insert SA_bufu[0] into heap
5. for each SA_bufu
6. insert SA_bufu[0] into heap
Fig. 5. The pseudocode for buffer allocation as the initial step for merge.
Fig. 5. The pseudocode for buffer allocation as the initial step for merge.](https://image.slidesharecdn.com/suffix-tree-over-memory-140828232352-phpapp02/75/Sufix-Array-14-2048.jpg)
![CompareSuffix algorithm
15
Algorithm compareSuffix (Si from partition u,
Sj from partition v)
1. if (u = = v)
2. return -1 //Si lex Sj, since they are sorted
//in increasing order inside each partition
Algorithm compareSuffix (Si from partition u,
3. if (u v)
4. if (partitionBit in R_bufuv[Sj from partition v)
1. if (u = = v)
current pointer] = = 0)
5. return 2. return -1 -1 //Si lex Sj, //Si since they are sorted
lex Sj
6. else
//in increasing order inside each partition
7. return1 //Si lex Sj
8. if (u v)
9. if (partitionBit in R_bufvu[current pointer] = = 0)
10. return 1 //Sj lex Si
11. else
12. return -1 //Sj lex Si
3. if (u v)
4. if (partitionBit in R_bufuv[current pointer] = = 0)
5. return -1 //Si lex Sj
6. else
7. return1 //Si lex Sj
8. if (u v)
9. if (partitionBit in R_bufvu[current pointer] = = 0)
10. return 1 //Sj lex Si
11. else
12. return -1 //Sj lex Si
Fig. 6. Algorithm for suffix comparison which uses the pairwise suffix information from the order arrays
created during pairwise suffix sorting.
Algorithm for suffix comparison which uses the pairwise suffix information from the order during pairwise suffix sorting.](https://image.slidesharecdn.com/suffix-tree-over-memory-140828232352-phpapp02/75/Sufix-Array-15-2048.jpg)



![TDD which works with uncompressed inputs. The results 評価: 他⼿手法との⽐比較
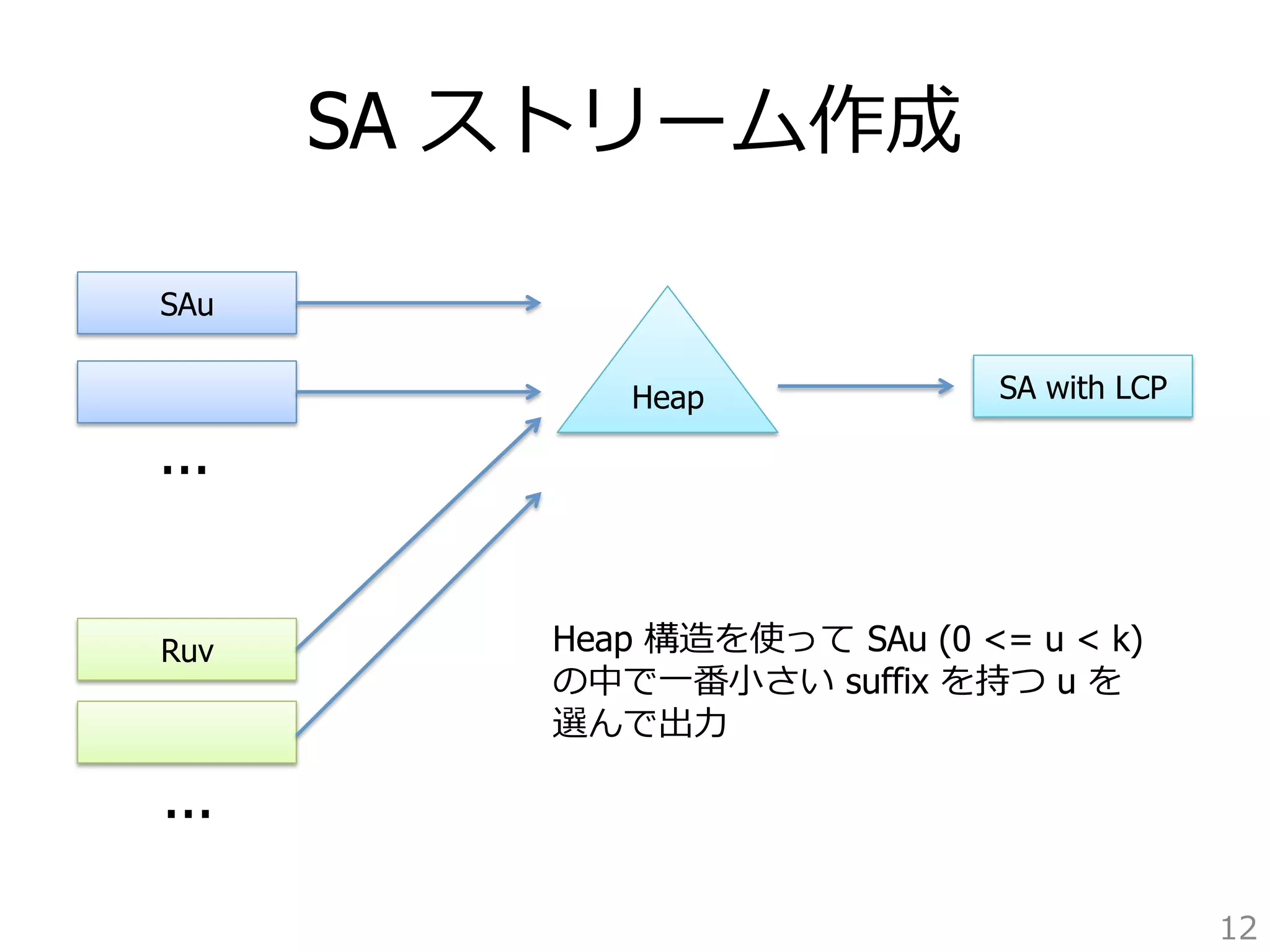
Program Time, hours
TDD 125
B2ST 3
• ⼊入⼒力力 3GB の DNA (1⽂文字1byte)
• 使⽤用メモリ 600MB
27
Trellis+SB 11
of different suffix tree construction algorithms for approximately which is larger than the total allocated main memory.
suffix tree for the above 3GB input in 125 hours. of Trellis+SB reported in [20]. The value in Figure similar settings on a comparable machine.
divided the 3GB into partitions of 1GB each and built](https://image.slidesharecdn.com/suffix-tree-over-memory-140828232352-phpapp02/75/Sufix-Array-27-2048.jpg)