Tri Merge Sorting Algorithm

Department of Mathematics

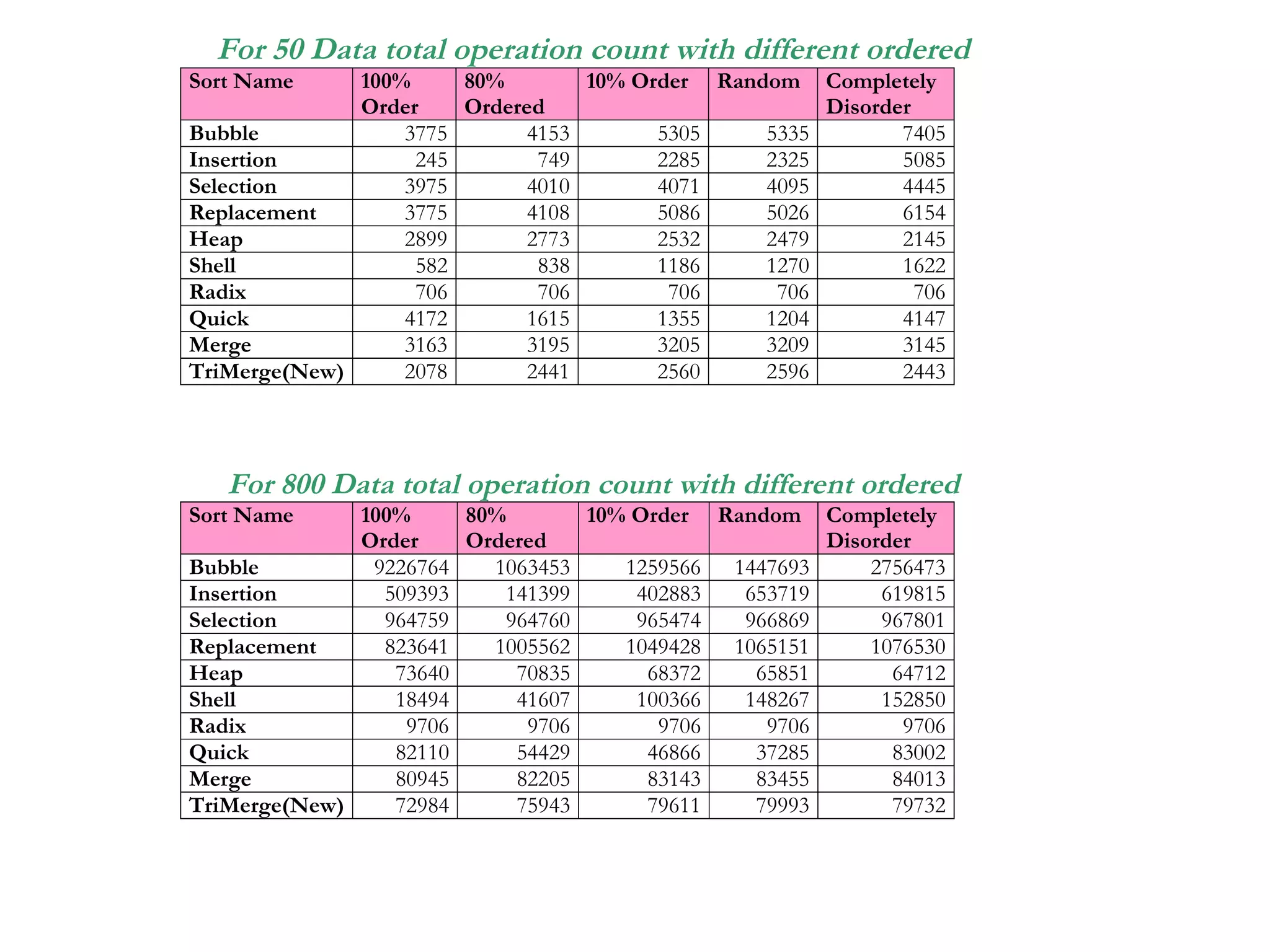
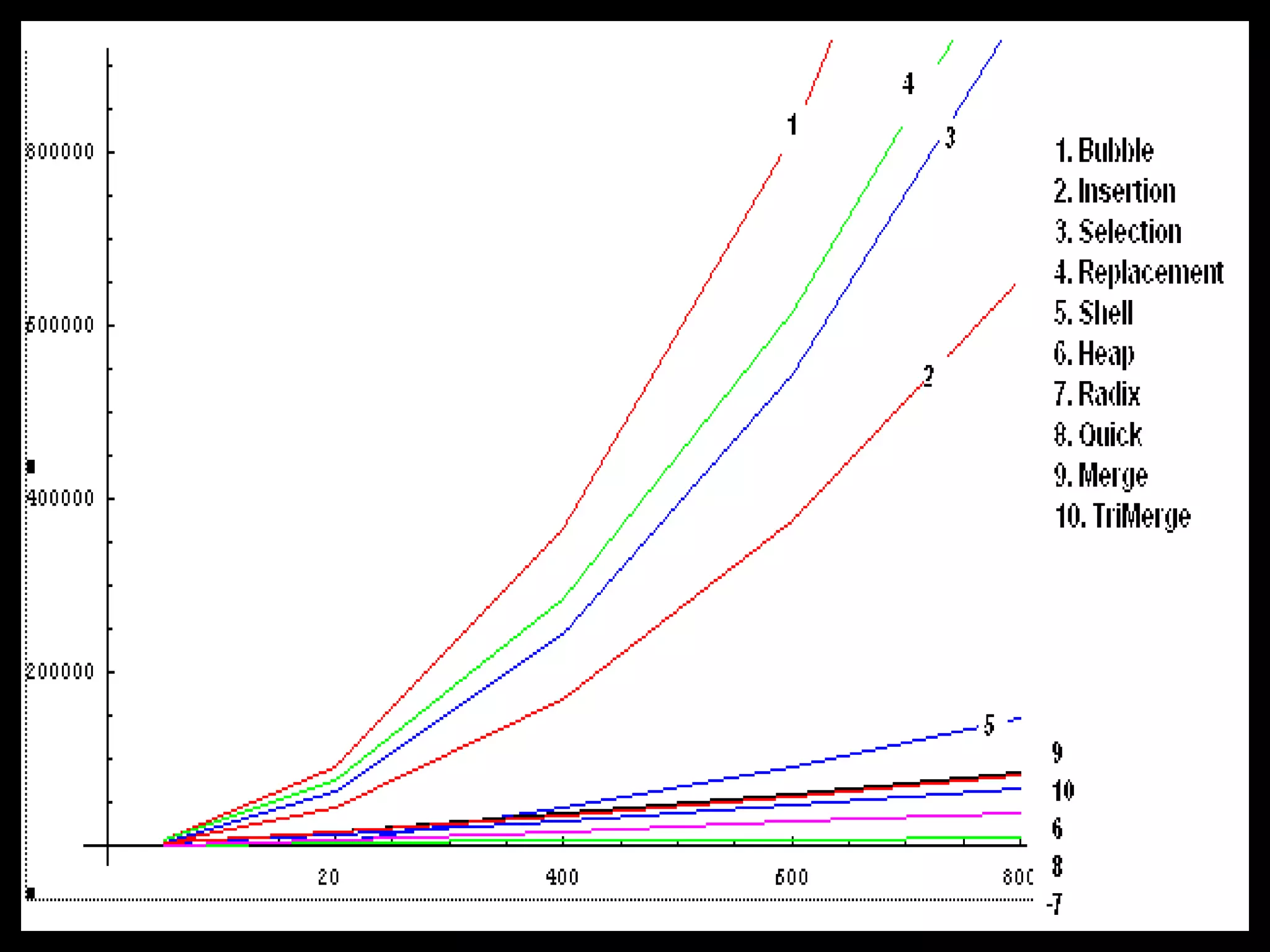
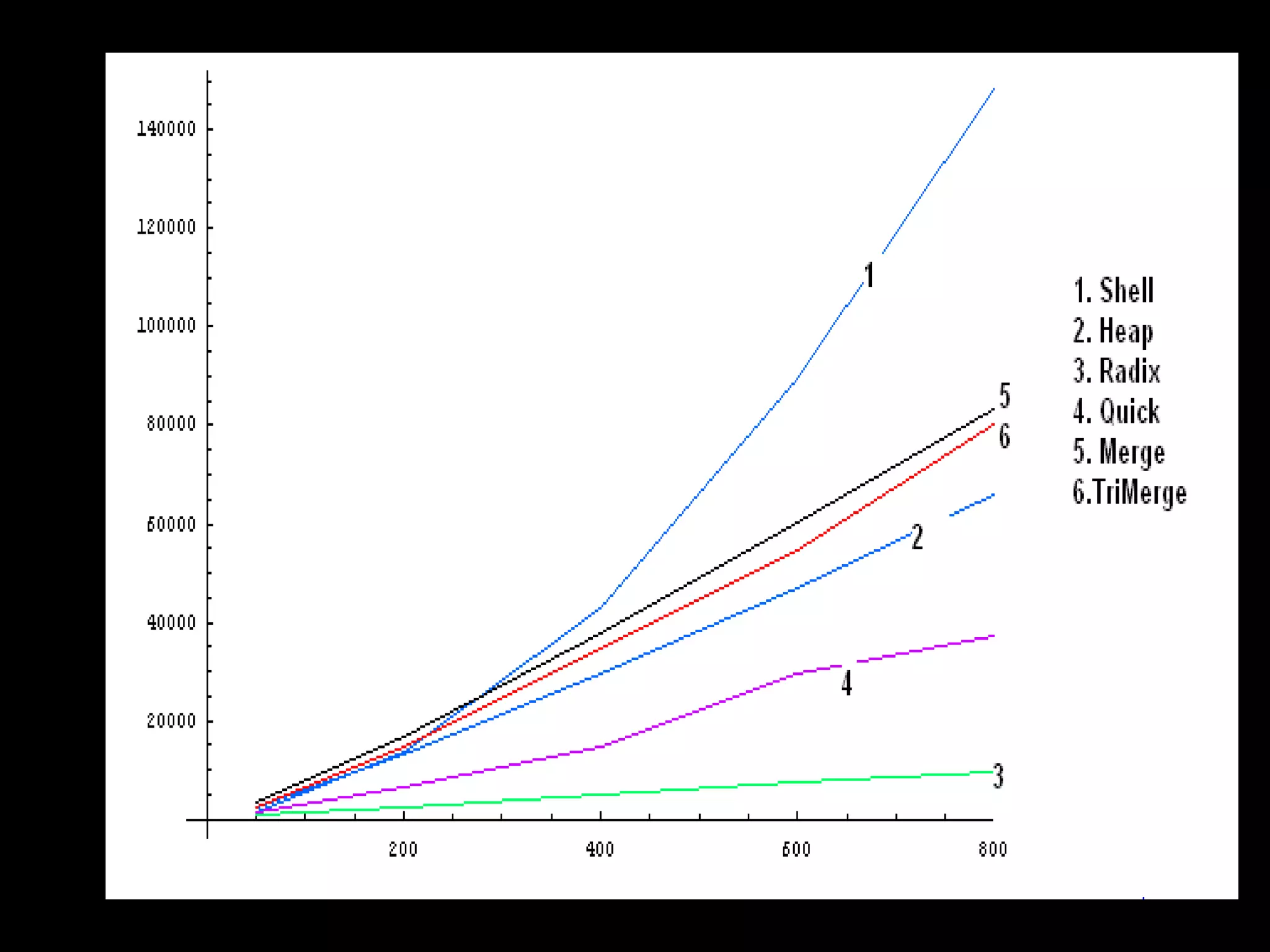
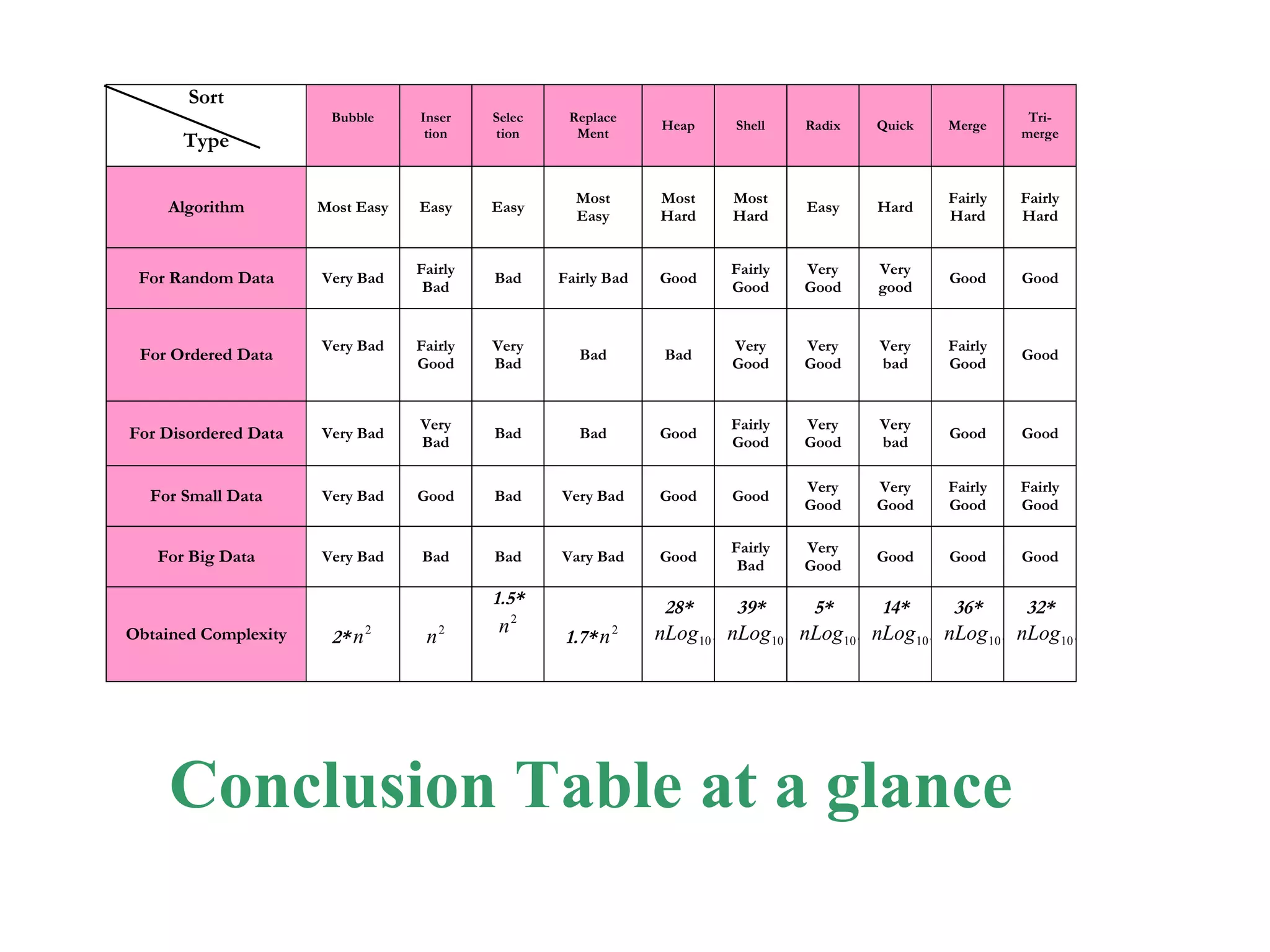
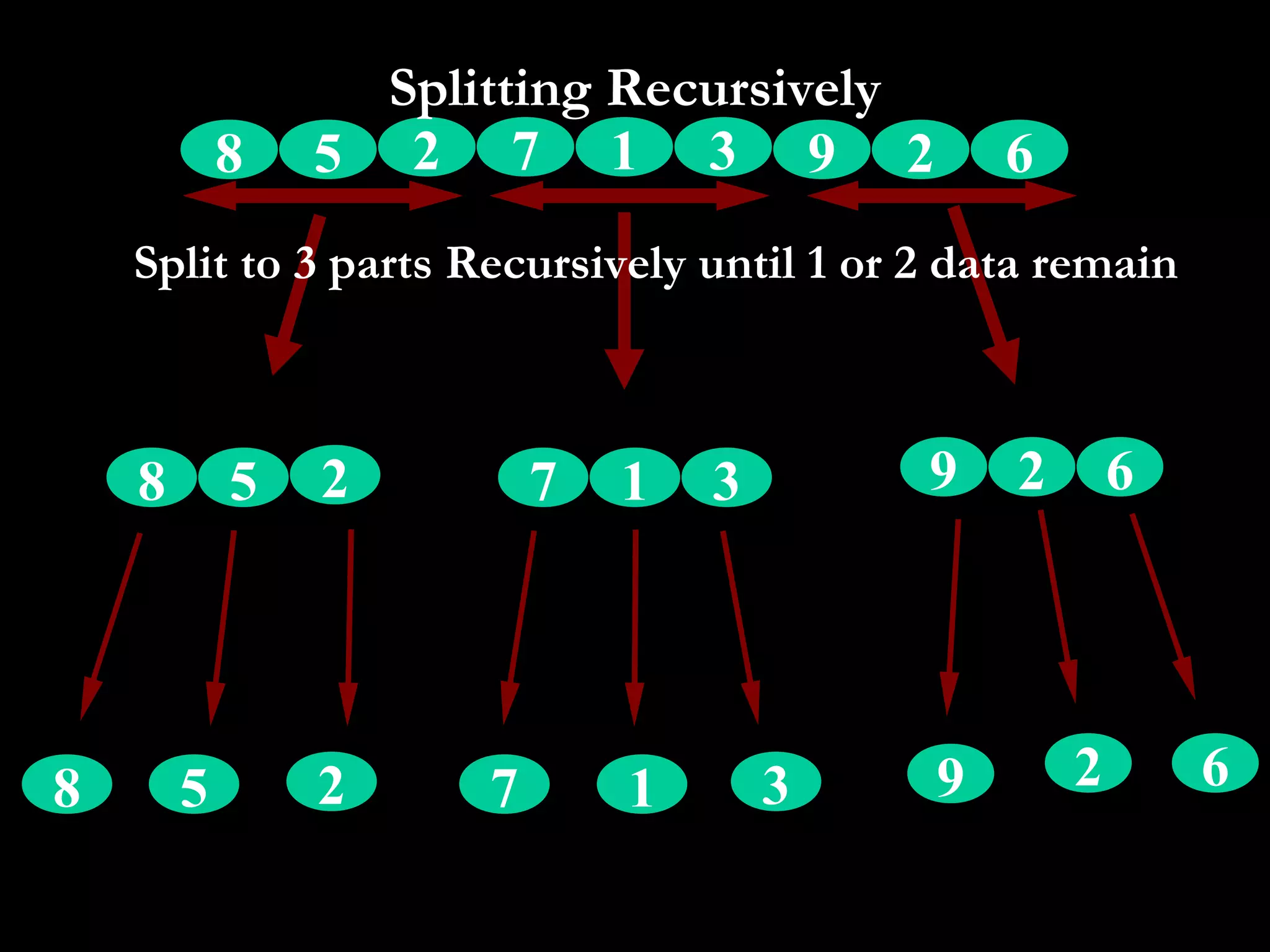
Dhaka University

Project Presentation
On
Efficiency of sorting algorithms
Course No: 490
Session: 2001- 2002
Class Roll No: Jn-262
Registration No: 3293/1997-1998

Supervised by: Dr. Amal Krishna Halder

What is sorting algorithms

• The word Sort refer to arrange the records
according order which may be ascending order
or descending order.

• The word Algorithm refer to technique or
process of sorting the records.

What we have done
• Review various sorting algorithms with the help of
Internet, Library books and our project guide.
• Implement the algorithms by a well known programming
language C/C++ and test it for various data.
• We contribute something new algorithm structure in the
sorting algorithm literature.
• We analyzed comparatively and try to find efficiency
among them.
• We try to make a Conclusion about the efficiency of
sorting algorithms.

Why we choose sorting algorithms
• There are many reasons why sorting algorithms is of
• Computer can perform million/billion time faster
interest to computer scientists and mathematicians.
operations than human. As for example, to find a specific
data among billion of data computer will take few
• seconds.
Some algorithms are easy to implement, some algorithms
take advantage of particular computer architectures, and
• some fast computer search a dataclever. Someits very
How algorithms are particularly depends on are
efficient in every stage, some are inefficient for a
processing power. Processing power depends on
particular size and type of data. to search a specific data
processing technique. It is easy
if it has been sorted earlier. So sorting takes very
• important role for searching data. find out the efficiency
In our project, our main aim is to
of various types of sorting algorithm.

Type of sorting
• Internal: if the records that it is sorting are in
main memory. e.g. Bubble, Quick, Shell etc.

• External: if the records that it is sorting are with
the help of auxiliary storage. e.g. Radix, Merge,
Tri-merge(newly proposed)

A sort also can classified as:

• Recursive: if recursive function (the function
which calls itself in the function) is used .
e.g. Merge, Quick, Tri-merge(newly proposed)
etc.

• Non-recursive: if it is not used recursive
function e.g. Bubble, Insertion, Shell etc.

Overview
• After reviewing various sorting algorithm we
choose some commonly used sorting algorithm
that will be listed afterwards.

• For each algorithm we try to describe
derivation and algorithm with the same
example for clear understand.

Some Common Sorting Algorithms:
⇒Bubble Sort
⇒Insertion Sort
⇒Selection Sort
⇒Replacement Sort
⇒Shell Sort
⇒Heap Sort
⇒Radix Sort
⇒Quick Sort
⇒Merge Sort

A new approach for sorting algorithm
literature
• Reviewing various sorting algorithm our knowledge has
been enriched. We try to work with ternary tree structure
for sorting algorithm where as generally used binary tree
structure.
• After facing many problem finally we able to construct a
successful sorting algorithm which probed to be more
efficient than binary one.
• Since it uses ternary tree structure and merging technique
we named it Tri-merge Sort.
• As far as our knowledge goes, this ternary tree structure
has not yet been used for sorting algorithm.

Problem faced
• At first we faced the problem that if data size can be
expressed as 3 i (i=1,2…k) then it works properly
because it splits equally and merge without missing

• But if data size is not an exact multiple of 3 then it
cannot be split equally and cannot merge from three
files recursively.

• We fixed the problem by ensuring that data will be
split recursively until 1 or 2 data remain. This last step
is treated individually without recursive call and will be
sort among themselves.

Tri-merge Sort
Formulation:
Tri-merge is a new proposed technique for sorting
data. It uses the attractive features of the sorting methods
as like of merge sorting. Tri-merge uses ternary tree
structure and recursive function.
The procedure of Tri-merge sort is completed in
two phases:

Phase-1: Split in to 3 parts recursively.
Phase-2: Merge to 1 part from 3 ordered parts recursively.

Phase-1: Split
• In this stage total data of the given list split into
3 parts.
• Each part consequently split 3 parts recursively
until 1 or 2 elements remain.
• When two data remain in a part they are sorted
among themselves.

• The split procedure will be shown afterward by
animation.

Phase-2: Merge
• In this phase every 3 split parts become 1 part
and are sorted among themselves.

• This process continues until all data become
one part and finally we get completely sorted
data.

• The merge procedure will be shown afterward
by animation.

Splitting Recursively
8 5 2 7 1 3 9 2 6
Split to 3 parts Recursively until 1 or 2 data remain

8 5 2 7 1 3 9 2 6

8 5 2 7 1 3 9 2 6

Merging Recursively

8 5 2 7 1 3 9 2 6

2 5 8 1 3 7 2 6 9

Compare first element from three files and find smallest one
Which will be merge to final 3 Sorted files tohere..
Final Merge From list as like describing 1 Sorted file

This process will be continue
until all data are merged

1 2 2 3 5 6 7 8 9
Now we get sorted list

Tri-mergeSort( a[L,....,R], L, R )
{ n=R-L+1 (number of element calculated from index position)
IF (n>2) THEN
{
m1 = n/3 (First midpoint)
m2 = 2*m1 (Second midpoint)
Tri-mergeSort ( a[L,….,m1], L, m1 )
Algorithm of Tri-merge sort
Tri-mergeSort ( a[m1+1,….,m2], m1+1, m2 )
Tri-mergeSort ( a[m2+1,….,R], m2+1, R )
Tri-merge ( a[L,….,R], L, m1+1, m2+1, R )
} in
ELSE IF (n = 2) THEN
{
Structural PseudoCode
IF ( a[L] > a[R] )
{
temp = a[L]
a[L] = a[R]
a[R] = temp
}
}
}

Tri-merge ( a[L,….,R], L, m1, m2, R)
{ part1 = a[L,…,m1-1]; part2 = a[m1,…,m2-1]; part3 = a[m2,…,R]
TempArray[L,…,R]; n = R-L+1
IF ( n > 2 )
{ WHILE( part1, part2 and part3 has elements )
Comparing from 3 parts find minimum and set to TempArray.
WHILE( part1 and part2 has elements )
WHILE( part1 has elements )
set to TempArray.
WHILE( part2 has elements )
set to TempArray.
WHILE (part3 has elements)
set to TempArray.
}
RETURN TempArray
}

void TriMergeSort( int a[], int L, int R, long int asscount[],long int comcount[])
{
int noOfEle=R-L+1;
int m1,m2,part,t;

comcount[0]++;
if(noOfEle>2)
{
part=(R-L+1)/3;
m1 = L+part-1;

Complete program of
m2 = L+2*part-1;
asscount[0]+=3;

Tri-merge Sort
TriMergeSort(a,L,m1,asscount,comcount);
TriMergeSort(a, m1+1,m2,asscount,comcount);
TriMergeSort(a, m2+1,R,asscount,comcount);

TriMerge(a,L,m1+1,m2+1,R,asscount,comcount);
}
else if(noOfEle==2)
{
comcount[0]+=2;
if(a[L]>a[R])
{
asscount[0]+=3;
t=a[L];
a[L]=a[R];

Efficiency Analysis
Efficiency of sorting algorithm depends on the
following criteria:
• How quickly (how much time require) data is sorted.
CPU time depends on how many operation (assignment
and compare) count are required for the algorithm
• How they work for small data
• How they work for big data
• How they work for random data
• How they work for preordered, disordered data and so
on.

To achieve our goal we have try to do the
following task
Since efficiency (time) depends on number of operations
so we try to find out the total number of assignment and
compare operations involved.
• Input data is prepared as random order by C/C++
programming command.
• To get effect on number of operations for small and big
data we find out total number of operations for 50, 200,
400, 600, 800 data.
• We had a limitation to work with huge data (e.g. we have
used earlier version of C/C++ compiler, Limited
memory size of the computer.)

To achieve our goal we have try to do the
following task
For comparative analysis we arrange total number of
operation count in different table with different number
of data (e.g. 50, 200, 400, 600, 800) including 100%, 80%,
10%, random, totally disordered.
• To compare the result clearly we show them graphically
so that one can get the picture at a glance.
• Analyzing the obtained data we try to find out an
approximation function of operation count f(n), where n
is the number of data. To get the function we use the
technique of interpolation. This function is also serves
an indication about the efficiency of the algorithm.

For 50 Data total operation count with different ordered
Sort Name 100% 80% 10% Order Random Completely
Order Ordered Disorder
Bubble 3775 4153 5305 5335 7405
Insertion 245 749 2285 2325 5085
Selection 3975 4010 4071 4095 4445
Replacement 3775 4108 5086 5026 6154
Heap 2899 2773 2532 2479 2145
Shell 582 838 1186 1270 1622
Radix 706 706 706 706 706
Quick 4172 1615 1355 1204 4147
Merge 3163 3195 3205 3209 3145
TriMerge(New) 2078 2441 2560 2596 2443

For 800 Data total operation count with different ordered
Sort Name 100% 80% 10% Order Random Completely
Order Ordered Disorder
Bubble 9226764 1063453 1259566 1447693 2756473
Insertion 509393 141399 402883 653719 619815
Selection 964759 964760 965474 966869 967801
Replacement 823641 1005562 1049428 1065151 1076530
Heap 73640 70835 68372 65851 64712
Shell 18494 41607 100366 148267 152850
Radix 9706 9706 9706 9706 9706
Quick 82110 54429 46866 37285 83002
Merge 80945 82205 83143 83455 84013
TriMerge(New) 72984 75943 79611 79993 79732

Approximate Operation count function f(n) with
respect to number of data n
Name of sorting algorithm f(n)=Number of operation count
(n = Number of data)
Bubble 2*n2

Insertion n2

Selection 1.5*n2

Replacement 1.7*n2

Heap 28(n * Log n)

Shell 39(n * Log n)

Radix 5(n * Log n)

Quick 14(n * Log n)

Merge 36(n * Log n)

Tri-merge(New) 32(n * Log n)

Graphical Representation
According
Operation Count Function

Bubble Sort is a very slow way of sorting; its
main advantage is the simplicity of the
algorithm.
Insertion Sort is much efficient for ordered,
preordered and small data. For disorder and
large data its efficiency goes inversely.

Selection sort works nearly same for all types
(ordered, preordered, random, disordered) of
data. It is more efficient for small data than
large one.
Replacement sort is also a slow procedure as
bubble sort, it is not so efficient one.
Heap sort works well for disordered and data
than preordered data. It also works well for
big data.

Shell sort is more efficient for ordered data; it
also works very well for small data but very
slow for disordered data.
Radix sort is much more efficient than any
other sorting algorithm. It works well for all
types of ordered, disordered and random
data; basically it gives exactly the same
number of operations for all of those types.
In our observation
Quick sort is more efficient for random data. It
is bad for fully ordered and fully disordered
data.
Merge sort gives nearly same number of
operation for all types of data. It is more
efficient for big data.
Tri-merge sort gives much better result than the
merge sort, i.e. it is more efficient than
merge.

Ranking of sorting algorithm:

It is very difficult to make ranking order of sorting algorithm according to
their efficiency. Some works very well for small data and some well for big
data. Similarly some works well for preordered data some works well for
random data. After all we try to find out a general rank order for average
situation.
 Radix sort
 Quick sort
 Heap sort
 Tri-merge (newly proposed)
 Merge sort
 Shell sort
 Insertion sort
 Selection sort
 Replacement sort
 Bubble sort.

Sort
Bubble Inser Selec Replace Tri-
Heap Shell Radix Quick Merge
tion tion Ment merge
Type

Most Most Most Fairly Fairly
Algorithm Most Easy Easy Easy
Easy Hard Hard
Easy Hard
Hard Hard

Fairly Fairly Very Very
For Random Data Very Bad
Bad
Bad Fairly Bad Good
Good Good good
Good Good

Very Bad Fairly Very Very Very Very Fairly
For Ordered Data Good Bad
Bad Bad
Good Good bad Good
Good

Very Fairly Very Very
For Disordered Data Very Bad
Bad
Bad Bad Good
Good Good bad
Good Good

Very Very Fairly Fairly
For Small Data Very Bad Good Bad Very Bad Good Good
Good Good Good Good

Fairly Very
For Big Data Very Bad Bad Bad Vary Bad Good
Bad Good
Good Good Good

1.5* 28* 39* 5* 14* 36* 32*
2 2 n2 2 nLog10 n nLog10 n nLog10 n nLog10 n nLog10 n nLog10 n
Obtained Complexity 2* n n 1.7* n

Conclusion Table at a glance

Tri Merge Sorting Algorithm

More Related Content

What's hot

Viewers also liked

Similar to Tri Merge Sorting Algorithm

More from Ashim Sikder

Recently uploaded

Tri Merge Sorting Algorithm