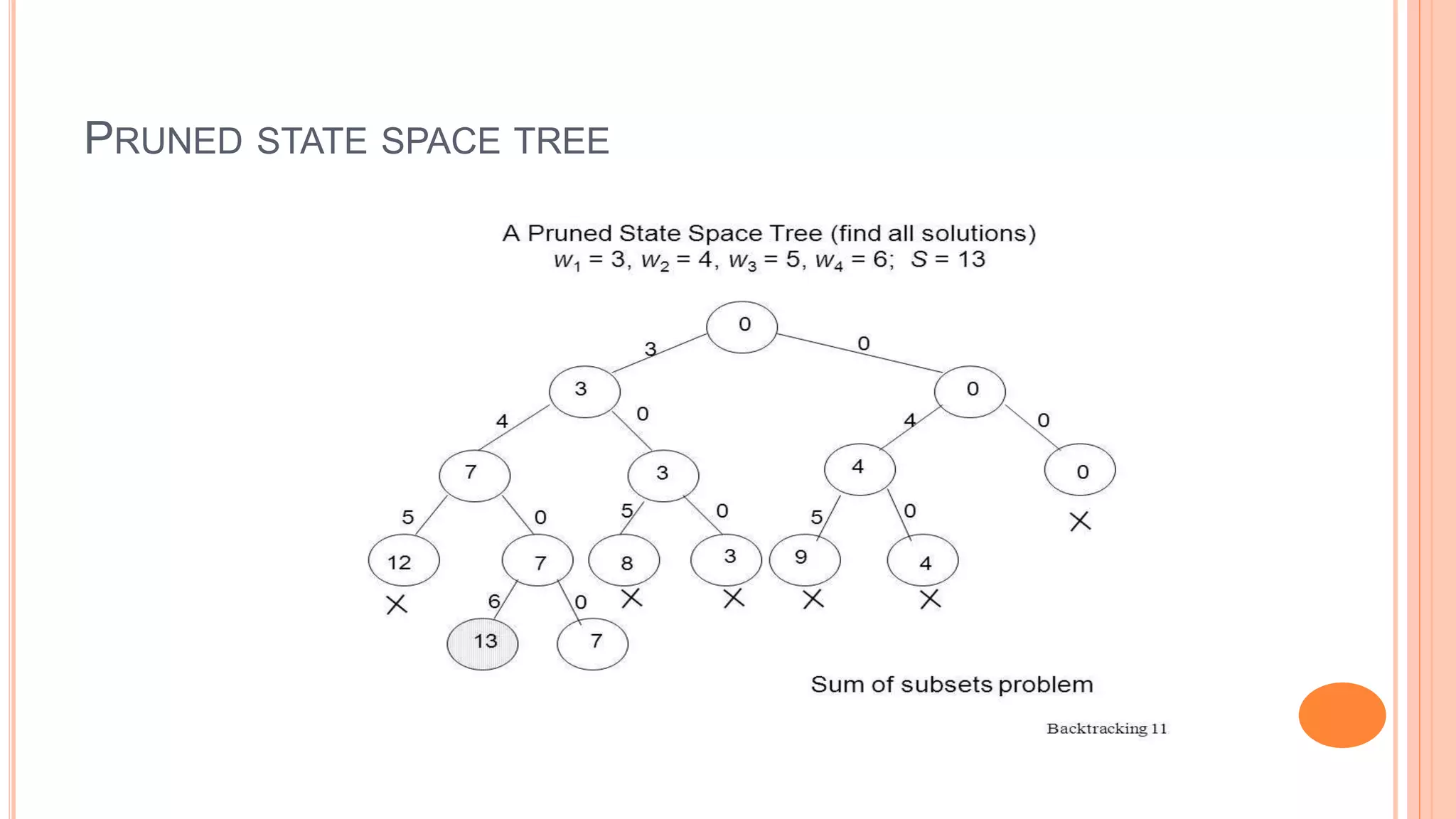
The document discusses the sum of subsets problem, which involves finding all subsets of positive integers that sum to a given number. It describes the problem, provides an example, and explains that backtracking can be used to systematically consider subsets. A pruned state space tree is shown for a sample problem to illustrate the backtracking approach. An algorithm for the backtracking solution to the sum of subsets problem is presented.


![SUM OF SUBSET PROBLEM
Backtracking Algorithm is used for Sum of subset problem.Using exhaustive
search we consider all subsets irrespective of whether they satisfy
given constraints or not.
Backtracking can be used to make a systematic consideration of the elements to be
selected.
Assume given set of 4 elements, say w[1] … w[4]. Tree diagrams can be used to
design backtracking algorithms. The following tree diagram depicts approach of
generating variable sized tuple.](https://image.slidesharecdn.com/sumofsubsetproblem-221208104947-16ac5efe/75/Sum-of-subset-problem-pptx-3-2048.jpg)




![ALGORITHM:
THE BACKTRACKING ALGORITHM FOR THE SUM OF SUBSETS PROBLEM
Problem: Given n positive integers (weights) and a positive integer w, determine all
combinations of the integers that sum to W.
Input: positive integer n, sorted ( non decreasing order) array of positive integer u indexed
from 1 to n, and a positive w.
Problem:
Void sum of subsets(index i , int weight , int total)
{
If (promising(i))
If (weight==w)
Cout<<include[1] through include[i];
Else
{
Include[i+1]=“yes”;
Sum_of_subsets (i+1, weight + w[i+1].total- w[i+1]);](https://image.slidesharecdn.com/sumofsubsetproblem-221208104947-16ac5efe/75/Sum-of-subset-problem-pptx-9-2048.jpg)
![.
Include[i+1]= “no” ;
Sum_of_subsets (i+1, weight, total- w[i+1]);
}
}
bool promising(index i);
{
Return(weight+total>=w)&&(weight==w||weight +w[i+1]
}](https://image.slidesharecdn.com/sumofsubsetproblem-221208104947-16ac5efe/75/Sum-of-subset-problem-pptx-10-2048.jpg)
