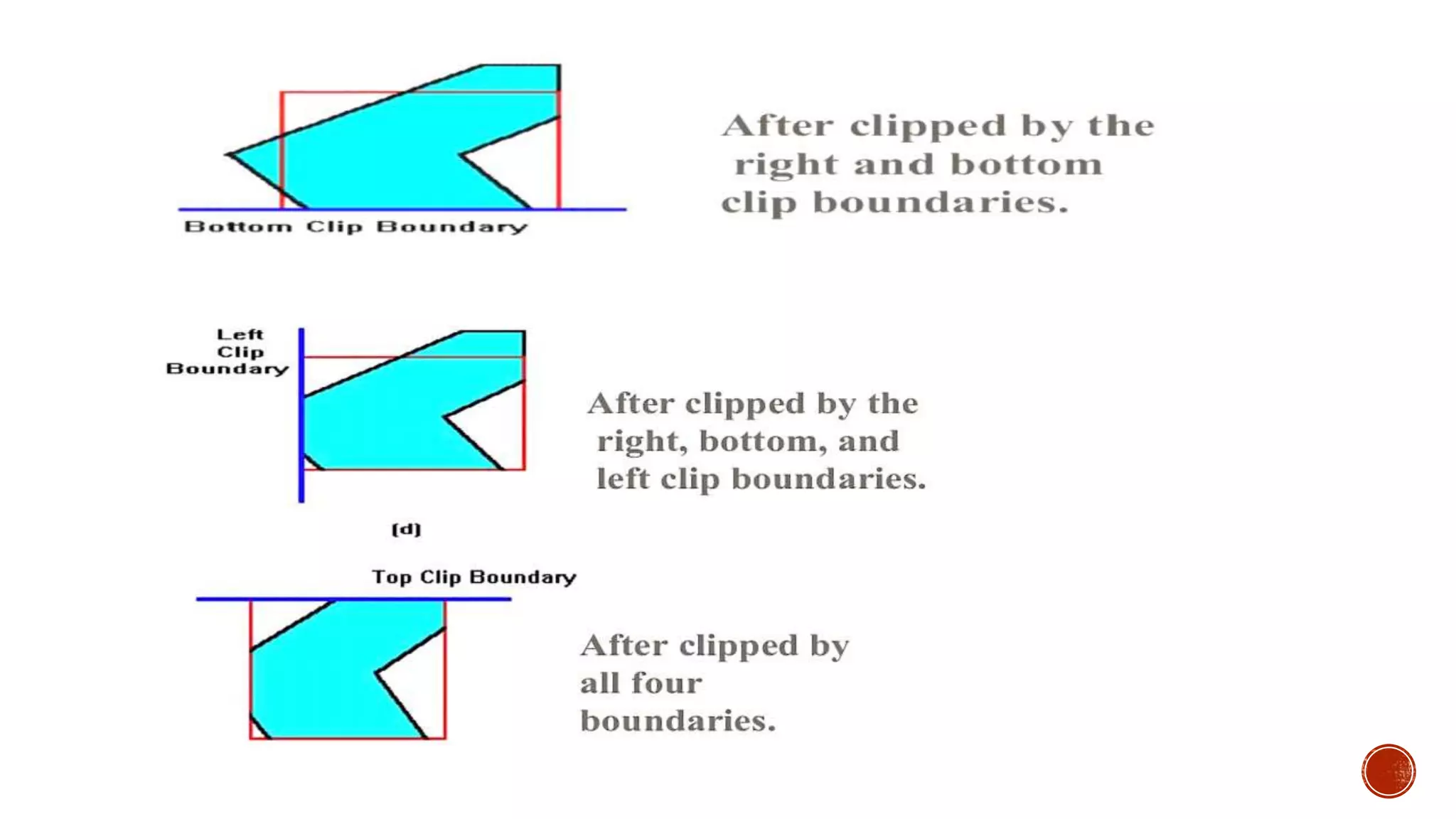
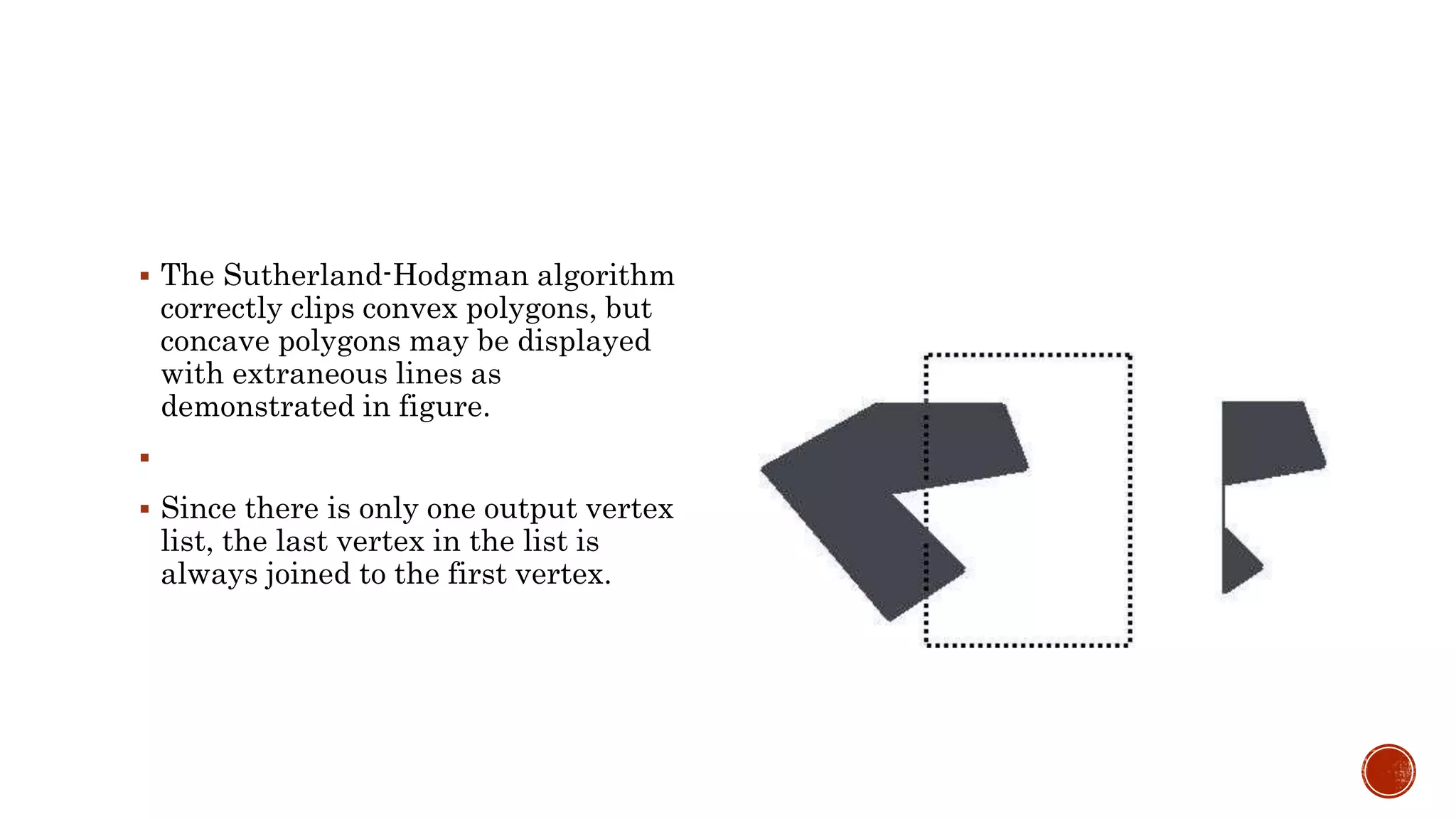
Sutherland hodgman polygon clipping algorithm

Sutherland hodgman polygon clipping algorithm

• 1.
   Generally, anyprocedure, that identifies that portion of a picture that are either inside or outside of a specified region of a space is referred as a clipping algorithm or simply clipping.
• 2.
   Clipping apolygon fill area needs more than line-clipping of the polygon edges -would produce and unconnected set of lines  Must generate one or more closed polylines, which can be filled with the assigned color or pattern
• 3.
   Each edgeof the polygon must be tested against each edge of the clip rectangle; new edges must be added, and existing edges must be discarded, retained, or divided. Multiple polygons may result from clipping a single polygon. We need an organized way to deal with all these cases.
• 4.
   Each edgegoes through 4 clippers. The rule for each edge for each clipper is:  If first input vertex is outside, and second is inside, output the intersection and the second vertex  If first both input vertices are inside, then just output second vertex  If first input vertex is inside, and second is outside, output is the intersection  If both vertices are outside, output is nothing
• 5.
  Polygons can beclipped against each edge of the window one at a time. Vertices which are kept after clipping against one window edge are saved for clipping against the remaining edges. Note that the number of vertices usually changes and will often increases.
• 8.
   The Sutherland-Hodgmanalgorithm correctly clips convex polygons, but concave polygons may be displayed with extraneous lines as demonstrated in figure.   Since there is only one output vertex list, the last vertex in the list is always joined to the first vertex.
• 9.
   Complexity ofthis algorithm will increase if number of edges of polygon increase. Algorithm has to calculate more number of intersection points over window boundary.  To overcome this problem we apply Weiler-Atherton Polygon Clipping Algorithm.