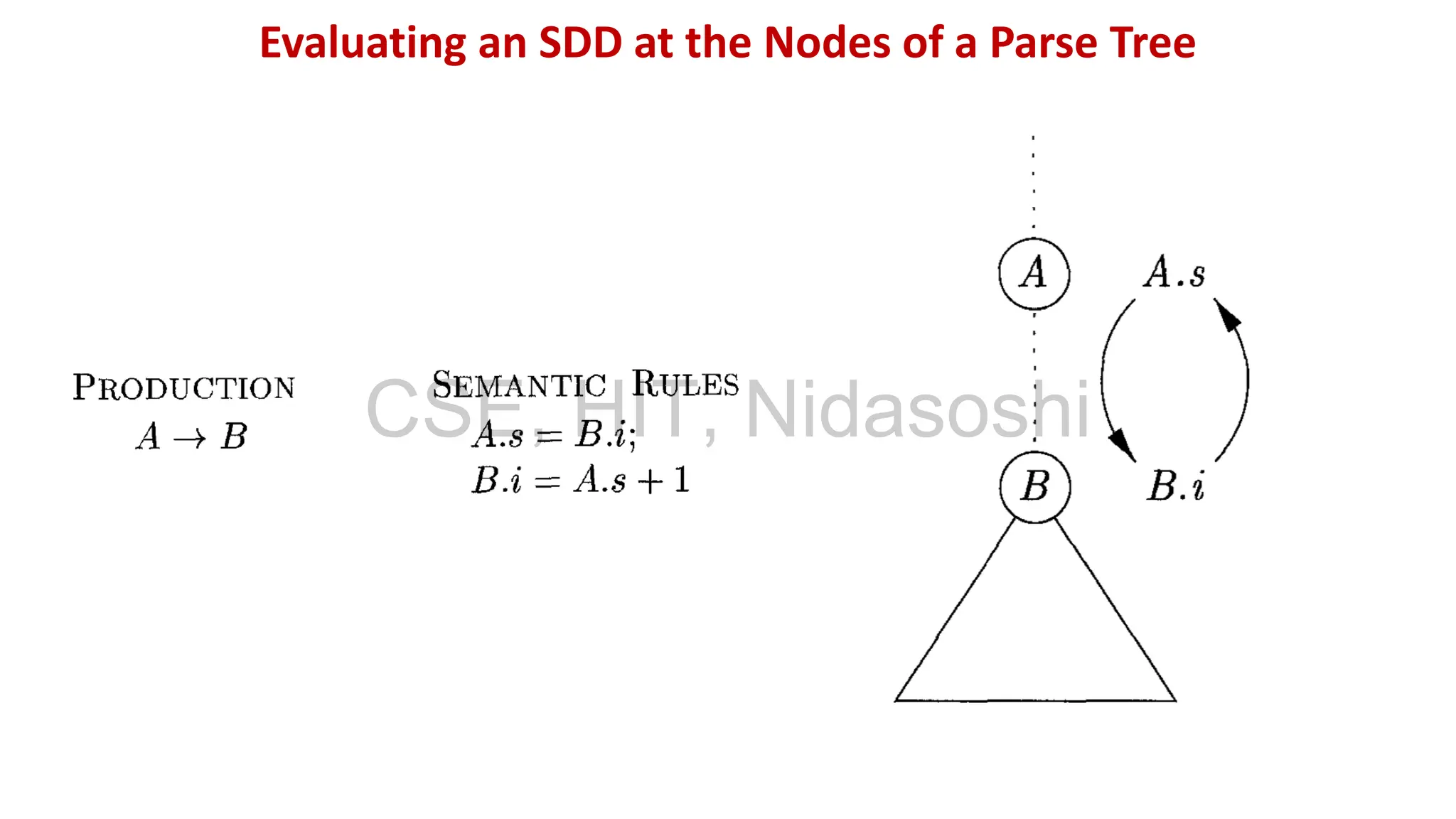
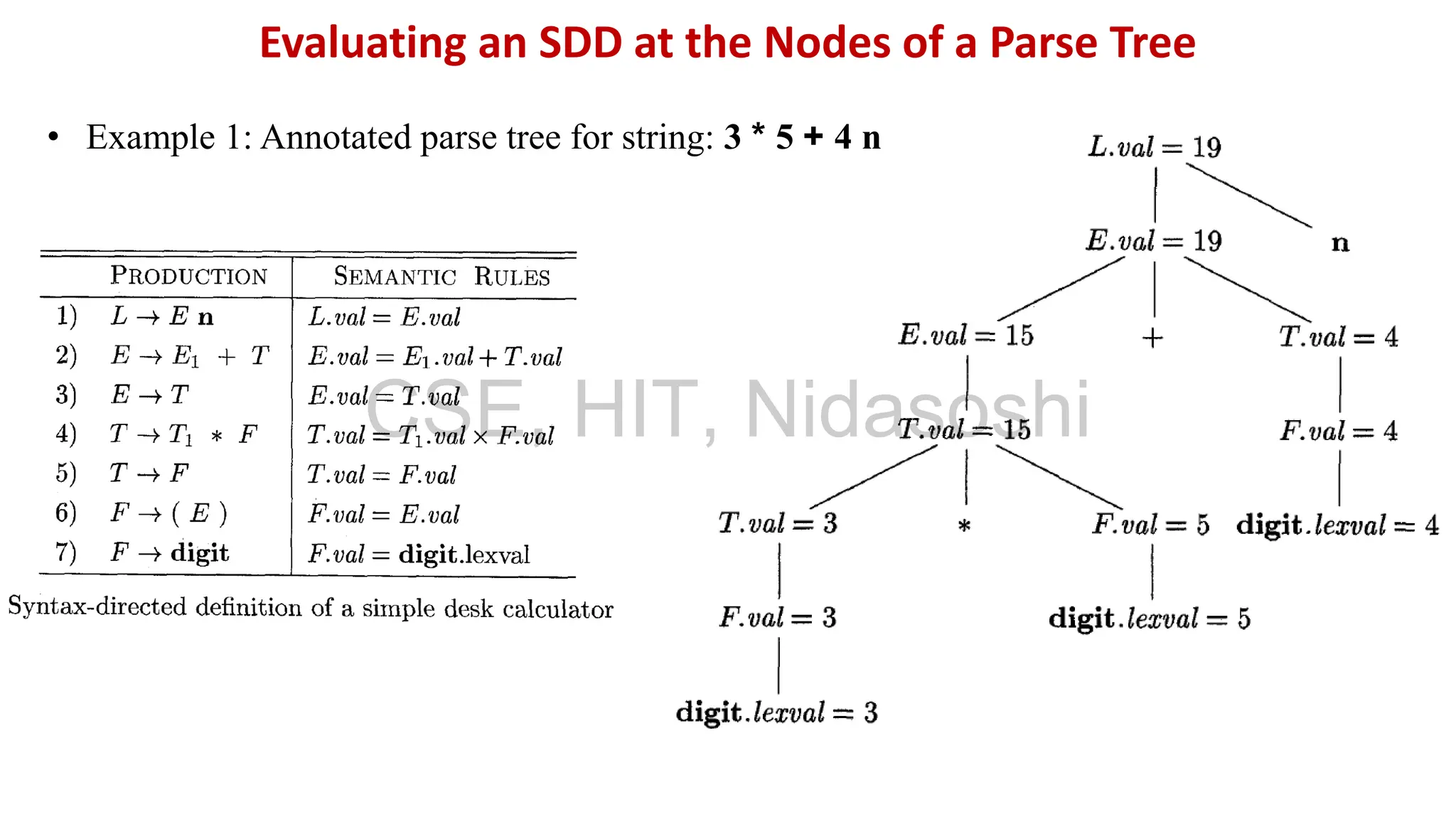
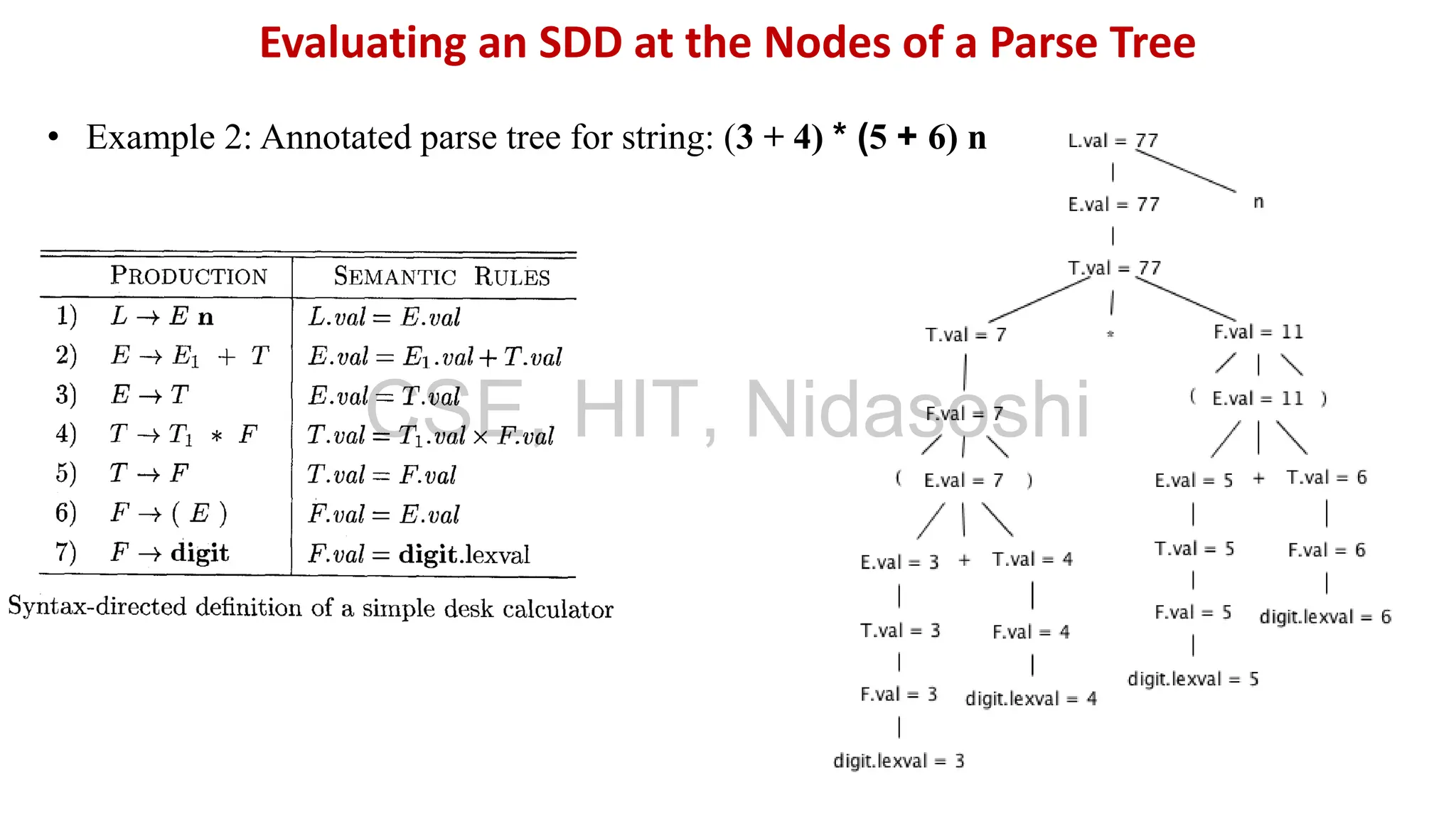
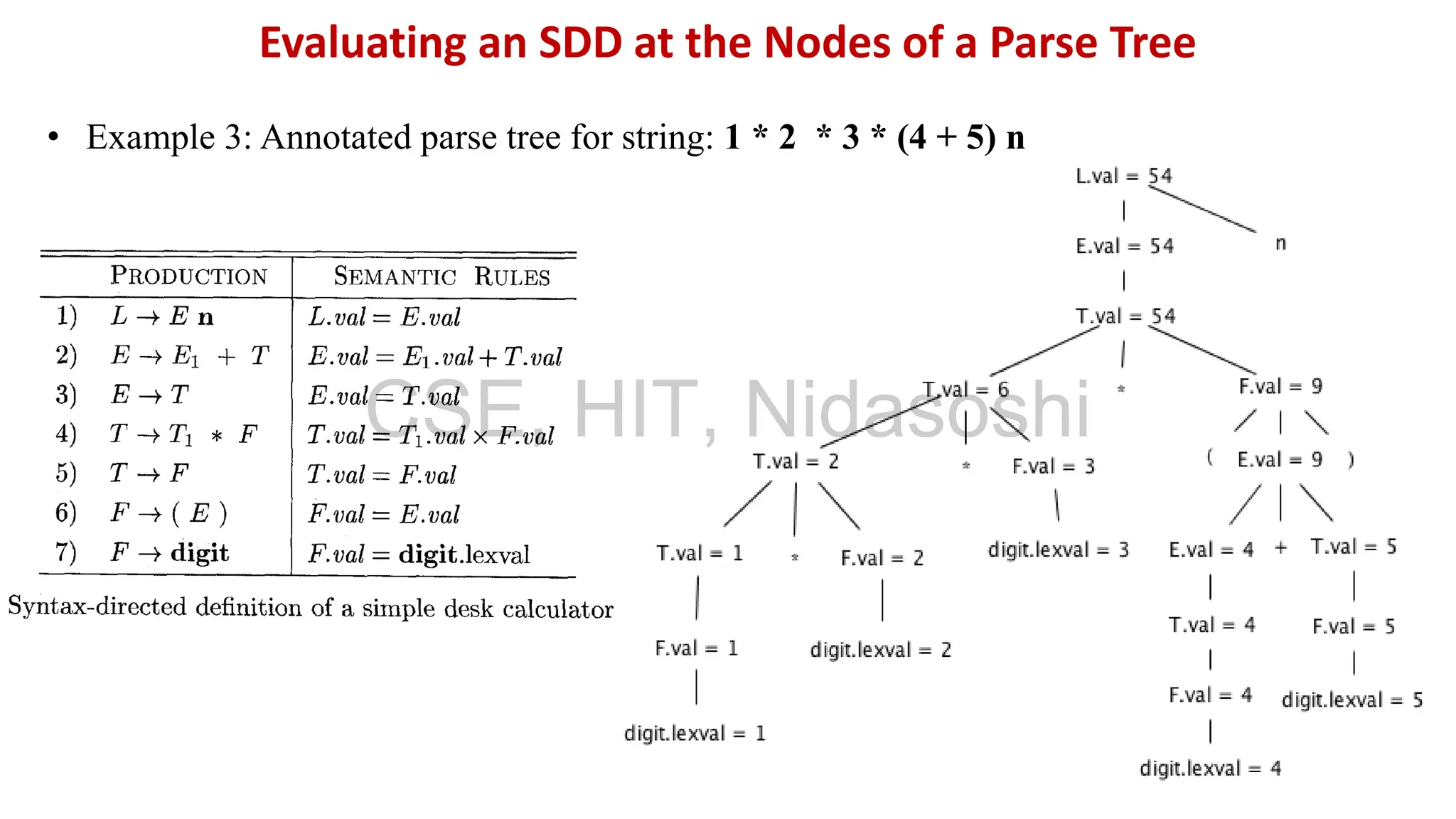
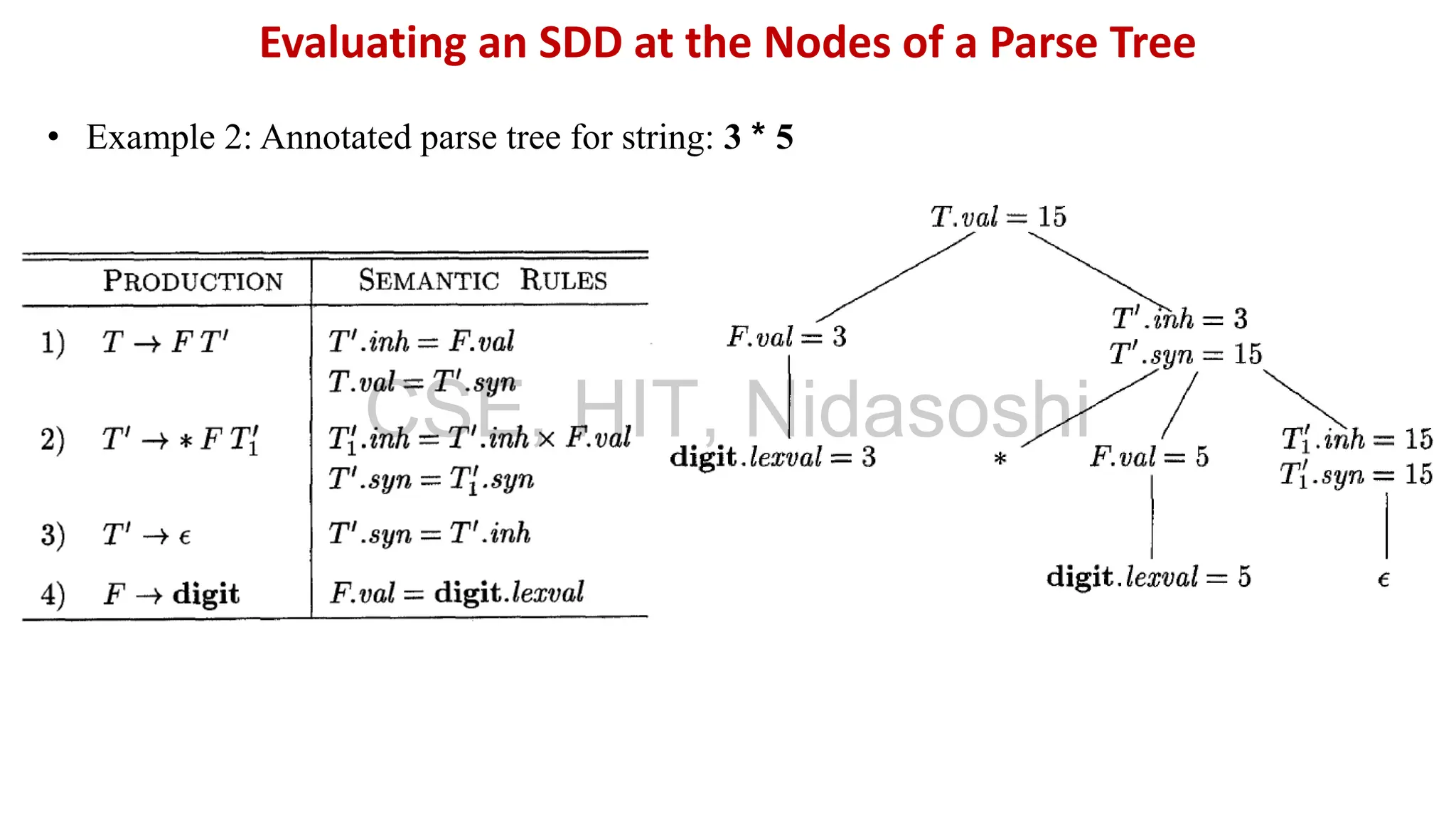
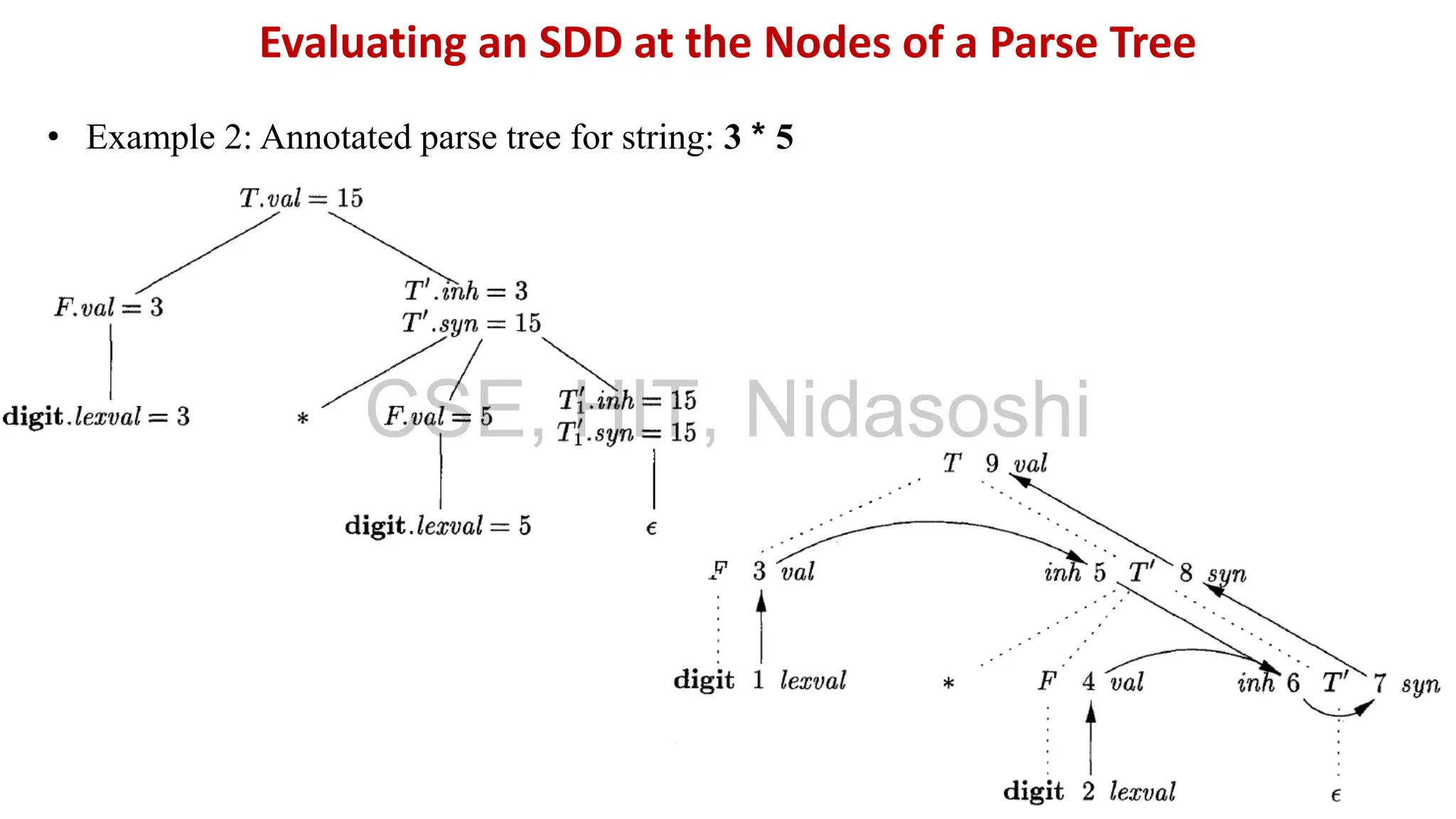
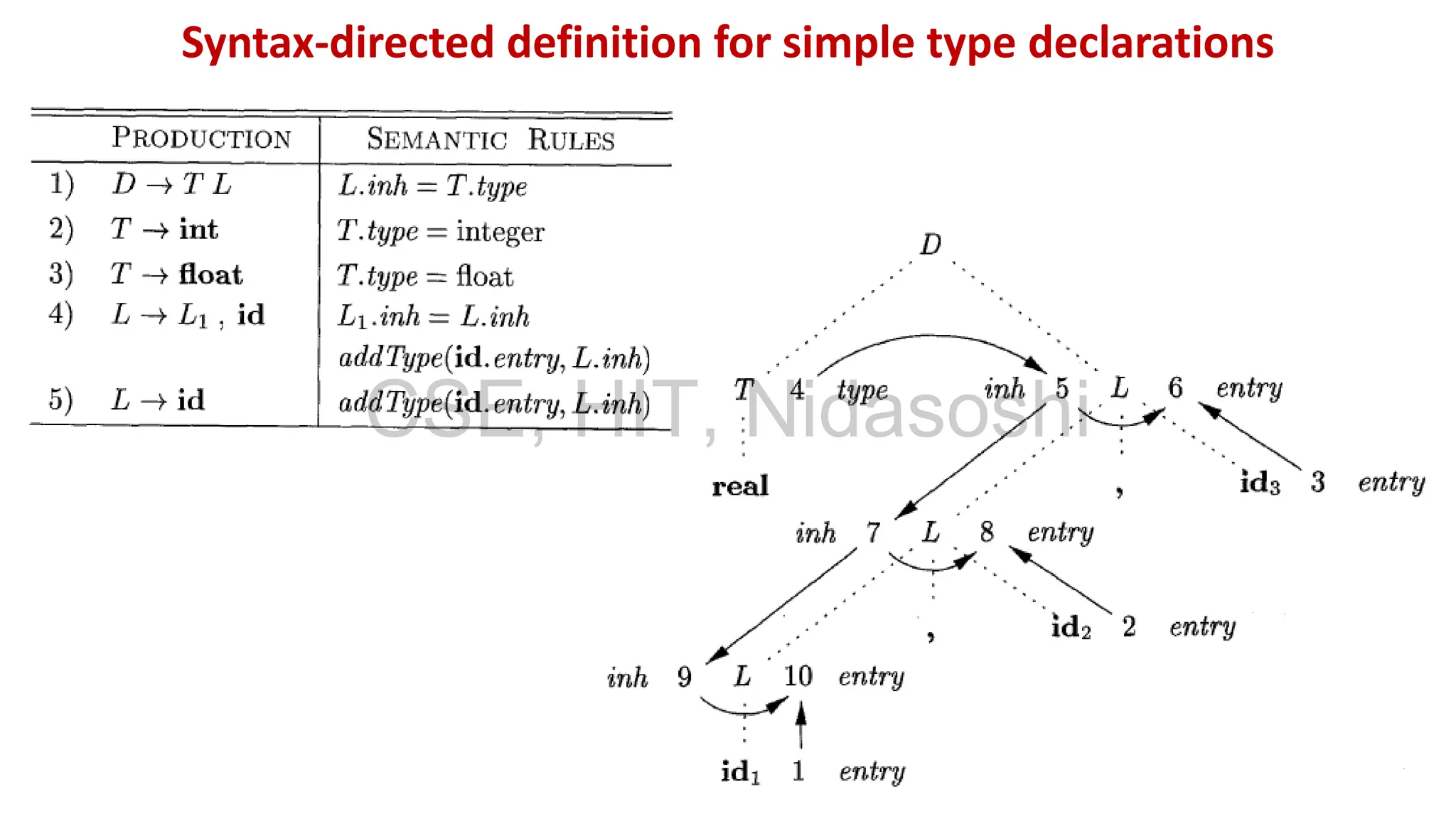
A syntax-directed definition (SDD) is a context-free grammar with attributes and semantic rules. Attributes are associated with grammar symbols and rules are associated with productions. An SDD can be evaluated on a parse tree to compute attribute values at each node. There are two types of attributes: synthesized attributes depend on child nodes, while inherited attributes depend on parent or sibling nodes. The order of evaluation is determined by a dependency graph showing the flow of information between attribute instances.























![2. The Structure of a Type – Example 1
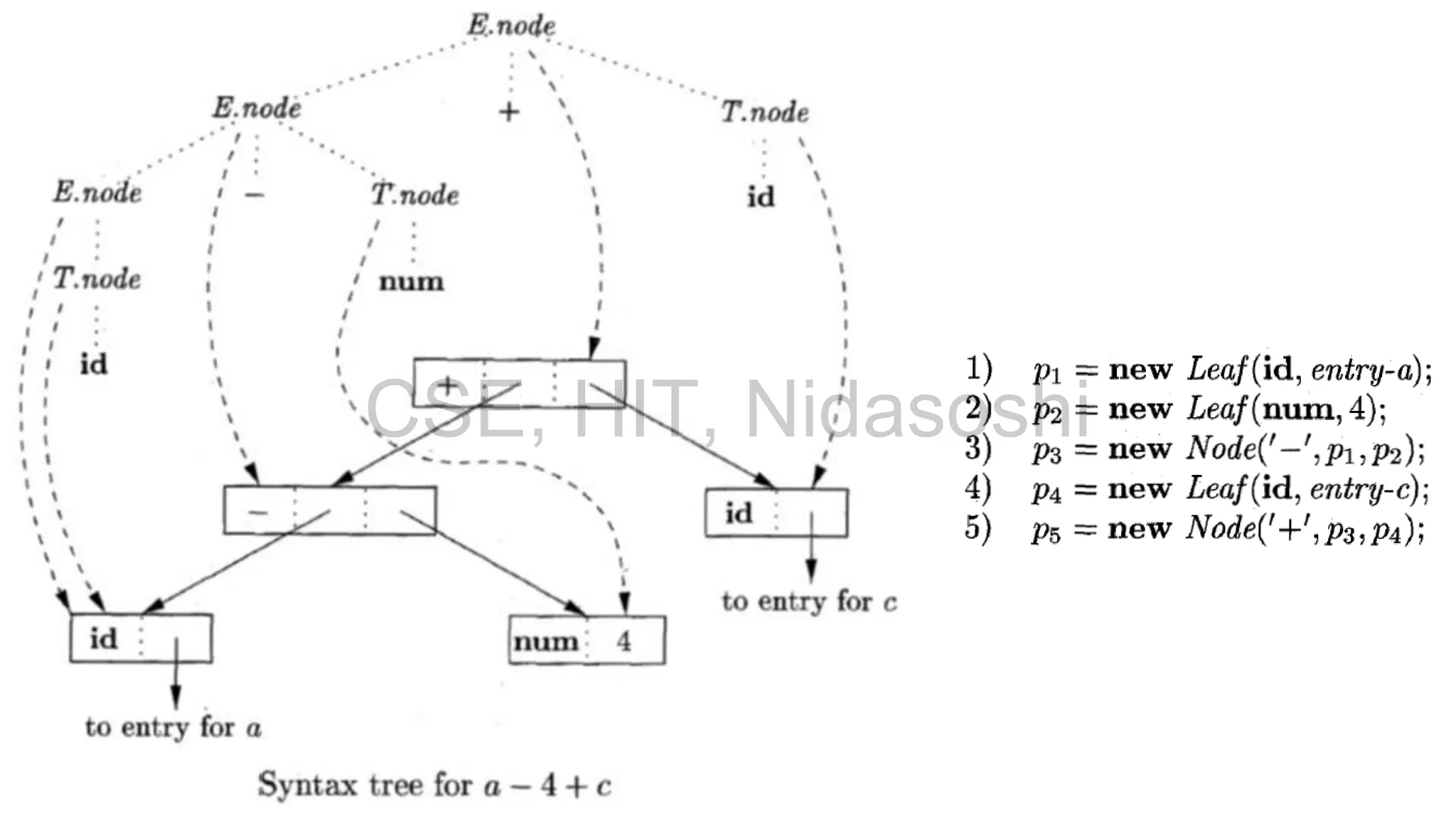
• In C, the type int [2][3] can be read as, "array of 2 arrays of 3 integers."
• The corresponding type expression array(2, array(3, integer)) is represented by the tree in
Fig.
• The operator array takes two parameters, a number and a type.
• If types are represented by trees, then this operator returns a tree node labeled array with two
children for a number and a type
Applications of Syntax-Direct ed Translation
CSE, HIT, Nidasoshi](https://image.slidesharecdn.com/sscmodule5-240205041747-95c90505/75/Syntax-Directed-Definition-and-its-applications-32-2048.jpg)

