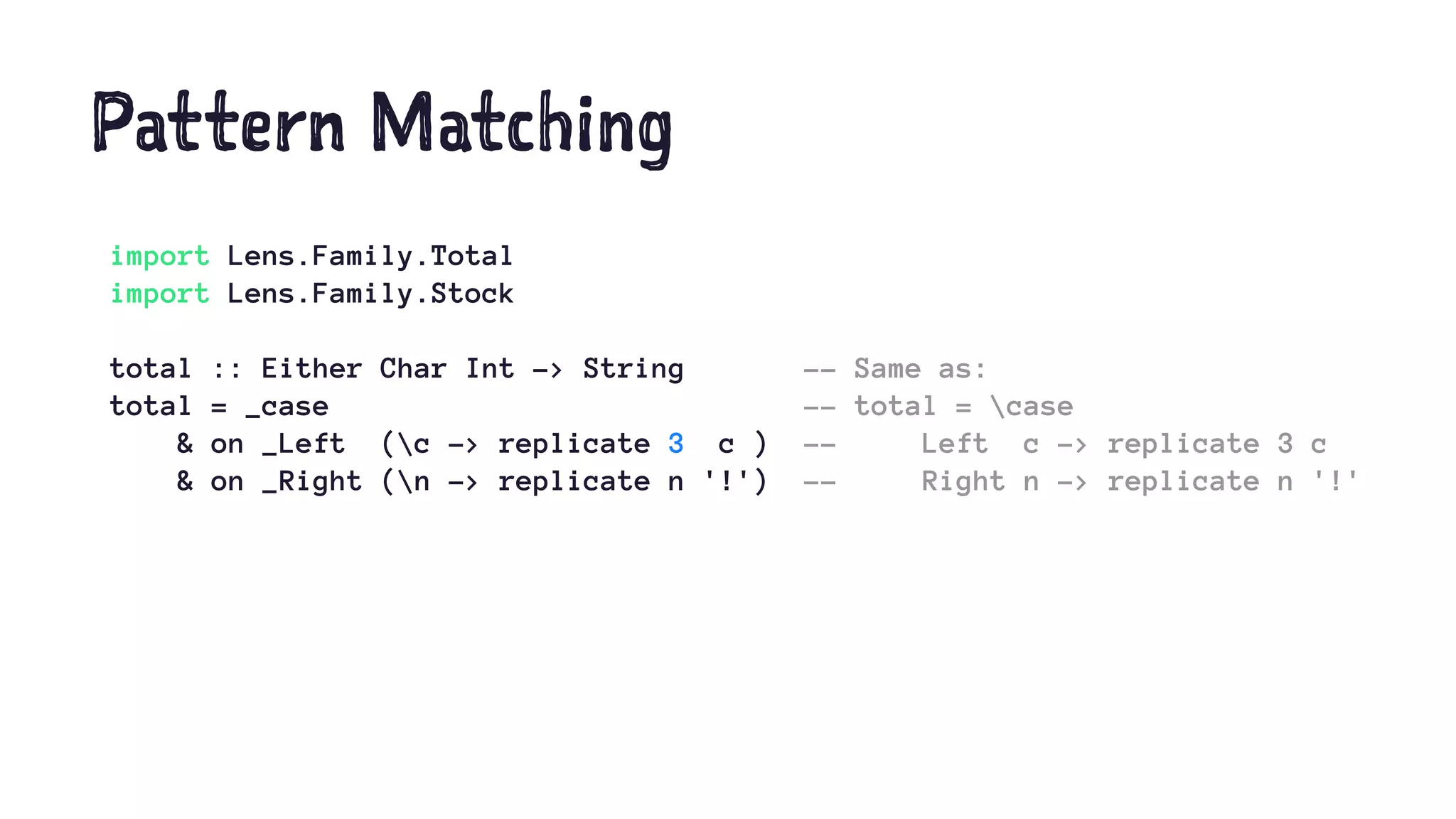
The document discusses the evolution and ideal characteristics of functional programming languages (FPLs), highlighting their features such as pattern matching, records, modules, and type classes. It contrasts various FPLs and proposes an ideal FPL that prioritizes ease of use, proof search capabilities, and zero-cost abstractions. The author calls for a structured editor to facilitate friendly functional programming and references several related projects for inspiration.









![[This Slide Intentionally Left Blank]](https://image.slidesharecdn.com/presentation-150526160835-lva1-app6892/75/The-Next-Great-Functional-Programming-Language-10-2048.jpg)





![Modules
structure ListStack :> STACK =
struct
type t = 'a list
[...]
end](https://image.slidesharecdn.com/presentation-150526160835-lva1-app6892/75/The-Next-Great-Functional-Programming-Language-17-2048.jpg)






























