Scala Functional Patterns

Continuations
and other Functional Patterns

Christopher League
Long Island University

Northeast Scala Symposium
 February 

Java classes → SML runtime
Standard ML of New Jersey v110.30 [JFLINT 1.2]
- Java.classPath := [”/home/league/r/java/tests”];
val it = () : unit
- val main = Java.run ”Hello”;
[parsing Hello]
[parsing java/lang/Object]
[compiling java/lang/Object]
[compiling Hello]
[initializing java/lang/Object]
[initializing Hello]
val main = fn : string list -> unit
- main [”World”];
Hello, World
val it = () : unit
- main [];
uncaught exception ArrayIndexOutOfBounds
raised at: Hello.main([Ljava/lang/String;)V
- ˆD

OO runtime ← functional languages

Scala
Clojure
F
etc.

Patterns
. Continuation-passing style
. Format combinators
. Nested data types

eme
Higher-order {functions, types}

Pattern : Continuations
A continuation is an argument that represents
the rest of the computation meant to occur
after the current function.

Explicit continuations – straight-line
def greeting [A] (name: String) (k: => A): A =
printk(”Hello, ”) {
printk(name) {
printk(”!n”)(k)
}}
def printk [A] (s: String) (k: => A): A =
{ Console.print(s); k }

scala> greeting(”Scala peeps”) { true }
Hello, Scala peeps!
res0: Boolean = true

Pay it forward...
Current function can ‘return’ a value
by passing it as a parameter to its continuation.

Explicit continuations – return values
def plus [A] (x: Int, y: Int) (k: Int => A): A =
k(x+y)
def times [A] (x: Int, y: Int) (k: Int => A): A =
k(x*y)
def less[A] (x: Int, y: Int) (kt: =>A) (kf: =>A):A =
if(x < y) kt else kf

def test[A](k: String => A): A =
plus(3,2) { a => times(3,2) { b =>
less(a,b) {k(”yes”)} {k(”no”)} }}

scala> test{printk(_){}}
yes

Delimited continuations
reset Serves as delimiter for CPS transformation.
shift Captures current continuation as a function
(up to dynamically-enclosing reset)
then runs speciﬁed block instead.

def doSomething0 = reset {
println(”Ready?”)
val result = 1 + ˜˜˜˜˜˜˜˜ * 3
println(result)
}
ink of the rest of the computation
as a function with the hole as its parameter.

val result = 1 + special * 3
println(result)
}
def special = shift {
k: (Int => Unit) => println(99); ”Gotcha!”
}
shift captures continuation as k
and then determines its own future.

val result = 1 + special * 3
println(result)
}
def special = shift {
k: (Int => Unit) => println(99); ”Gotcha!”
}

scala> doSomething1
Ready?
99
res0: java.lang.String = Gotcha!

Continuation-based user interaction
def interact = reset {
val a = ask(”Please give me a number”)
val b = ask(”Please enter another number”)
printf(”The sum of your numbers is: %dn”, a+b)
}

scala> interact
Please give me a number
answer using: submit(0xa9db9535, ...)
scala> submit(0xa9db9535, 14)
Please enter another number
answer using: submit(0xbd1b3eb0, ...)
scala> submit(0xbd1b3eb0, 28)
The sum of your numbers is: 42

Continuation-based user interaction
val sessions = new HashMap[UUID, Int=>Unit]
def ask(prompt: String): Int @cps[Unit] = shift {
k: (Int => Unit) => {
val id = uuidGen
printf(”%snanswer using: submit(0x%x, ...)n”,
prompt, id)
sessions += id -> k
}}
def submit(id: UUID, data: Int) = sessions(id)(data)

def interact = reset {
val a = ask(”Please give me a number”)
val b = ask(”Please enter another number”)
printf(”The sum of your numbers is: %dn”, a+b)
}

Pattern : Format combinators
[Danvy ]
Typeful programmers covet printf.
int a = 5;
int b = 2;
float c = a / (float) b;
printf(”%d over %d is %.2fn”, a, b, c);
Cannot type-check because format is just a string.
What if it has structure, like abstract syntax tree?

Typed format speciﬁers
val frac: Int => Int => Float => String =
d & ” over ” & d & ” is ” & f(2) & endl |
val grade: Any => Double => Unit =
”Hello, ”&s&”: your exam score is ”&pct&endl |>
val hex: (Int, Int, Int) => String =
uncurried(”#”&x&x&x|)
(Type annotations are for reference – not required.)

scala> println(uncurried(frac)(a,b,c))
5 over 2 is 2.50

scala> grade(”Joshua”)(0.97)
Hello, Joshua: your exam score is 97%
scala> println(”Roses are ”&s | hex(250, 21, 42))
Roses are #fa152a

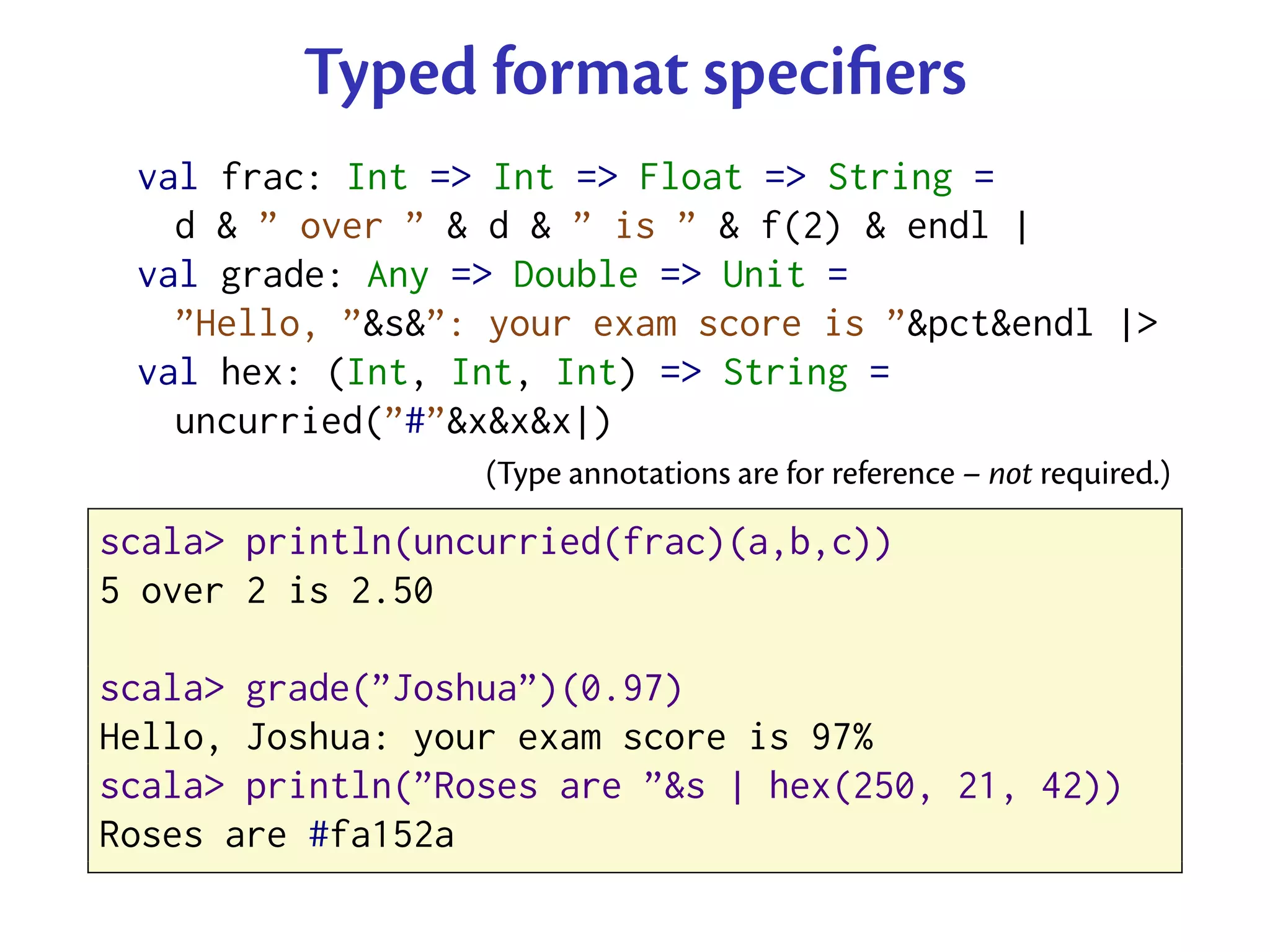
Buﬀer representation
type Buf = List[String]
def put(b: Buf, e: String): Buf = e :: b
def finish(b: Buf): String = b.reverse.mkString
def initial: Buf = Nil

Operational semantics
def lit(m:String)(k:Buf=>A)(b:Buf) = k(put(b,m))
def x(k:Buf=>A)(b:Buf)(i:Int) = k(put(b,i.toHexString))
def s(k:Buf=>A)(b:Buf)(o:Any) = k(put(b,o.toString))
(Not the actual implementation.)

lit(”L”)(finish)(initial) ”L”
x(finish)(initial)(42) ”2a”

where:
type Buf = List[String]
def put(b: Buf, e: String): Buf = e :: b
def finish(b: Buf): String = b.reverse.mkString
def initial: Buf = Nil

Function composition
(lit(”L”) & x) (finish) (initial) (2815)

lit(”L”)(x(finish)) (initial) (2815)

lit(”L”)(λ b0.λ i.finish(i.toHex :: b0)) (initial) (2815)

(λ b1.λ i.finish(i.toHex :: ”L” :: b1)) (initial) (2815)
finish(2815.toHex :: ”L” :: initial)
List(”aff”,”L”).reverse.mkString ”Laff”
where:
def lit(m:String)(k:Buf=>A)(b:Buf) = k(put(b,m))
def x(k:Buf=>A)(b:Buf)(i:Int) = k(put(b,i.toHexString))
def s(k:Buf=>A)(b:Buf)(o:Any) = k(put(b,o.toString))

Combinator polymorphism
What is the answer type?
x: ∀A.(Buf => A) => Buf => Int => A
finish: Buf => String

x(x(x(finish)))
A ≡ String
A ≡ Int => String
A ≡ Int => Int => String

Type constructor polymorphism
trait Compose[F[_],G[_]] { type T[X] = F[G[X]] }
trait Fragment[F[_]] {
def apply[A](k: Buf=>A): Buf=>F[A]
def & [G[_]] (g: Fragment[G]) =
new Fragment[Compose[F,G]#T] {
def apply[A](k: Buf=>A) = Fragment.this(g(k))
}
def | : F[String] = apply(finish(_))(initial)
}

Combinator implementations
type Id[A] = A
implicit def lit(s:String) = new Fragment[Id] {
def apply[A](k: Cont[A]) = (b:Buf) => k(put(b,s))
}

type IntF[A] = Int => A
val x = new Fragment[IntF] {
def apply[A](k: Cont[A]) = (b:Buf) => (i:Int) =>
k(put(b,i.toHexString))
}

Pattern : Nested data types
Usually, a polymorphic recursive data type
is instantiated uniformly throughout:
trait List[A]
case class Nil[A]() extends List[A]
case class Cons[A](hd:A, tl:List[A]) extends List[A]
What if type parameter of recursive invocation diﬀers?

Weird examples
trait Weird[A]
case class Wil[A]() extends Weird[A]
case class Wons[A](hd: A, tl: Weird[(A,A)])
extends Weird[A] // tail of Weird[A] is Weird[(A,A)]

val z: Weird[Int] = Wons(1, Wil[I2]())
val y: Weird[Int] = Wons(1, Wons((2,3), Wil[I4]))
val x: Weird[Int] =
Wons( 1,
Wons( (2,3),
Wons( ((4,5),(6,7)),
Wil[I8]())))

type I2 = (Int,Int)
type I4 = (I2,I2)
type I8 = (I4,I4)

Square matrices
[Okasaki ]
Vector[Vector[A]] is a two-dimensional matrix
of elements of type A.
But lengths of rows (inner vectors) could diﬀer.
Using nested data types, recursively build
a type constructor V[_] to represent a sequence
of a ﬁxed number of elements.
en, Vector[V[A]] is a well-formed matrix,
and V[V[A]] is square.

Square matrix example
scala> val m = tabulate(6){(i,j) => (i+1)*(j+1)}
m: FastExpSquareMatrix.M[Int] =
Even Odd Odd Zero (((),((((),(1,2)),((3,4),(5,6))
),(((),(2,4)),((6,8),(10,12))))),(((((),(3,6)),((
9,12),(15,18))),(((),(4,8)),((12,16),(20,24)))),(
(((),(5,10)),((15,20),(25,30))),(((),(6,12)),((18
,24),(30,36))))))
scala> val q = m(4,2)
q: Int = 15
scala> val m2 = m updated (4,2,999)
m2: FastExpSquareMatrix.M[Int] =
Even Odd Odd Zero (((),((((),(1,2)),((3,4),(5,6))
),(((),(2,4)),((6,8),(10,12))))),(((((),(3,6)),((
9,12),(15,18))),(((),(4,8)),((12,16),(20,24)))),(
(((),(5,10)),((999,20),(25,30))),(((),(6,12)),((
18,24),(30,36))))))

Analogy with fast exponentiation
fastexp r b 0 = r
fastexp r b n = fastexp r (b2 ) n/2 if n even
fastexp r b n = fastexp (r · b) (b2 ) n/2 otherwise
For example:
fastexp 1 b 6 = Even
fastexp 1 (b2 ) 3 = Odd
2
fastexp (1 · b2 ) (b2 ) 1 = Odd
2 22
fastexp (1 · b2 · b2 ) (b2 ) 0 = Zero
2
1 · b2 · b2

Fast exponentiation of product types
type U = Unit
type I = Int
fastExp U I 6 = // Even
fastExp U (I,I) 3 = // Odd
fastExp (U,(I,I)) ((I,I),(I,I)) 1 = // Odd
fastExp ((U,(I,I)),((I,I),(I,I))) // Zero
(((I,I),(I,I)),((I,I),(I,I))) 0 =
((U,(I,I)),((I,I),(I,I)))

Implementation as nested data type
trait Pr[V[_], W[_]] {
type T[A] = (V[A],W[A])
}
trait M [V[_],W[_],A]
case class Zero [V[_],W[_],A] (data: V[V[A]])
extends M[V,W,A]
case class Even [V[_],W[_],A] (
next: M[V, Pr[W,W]#T, A]
) extends M[V,W,A]
case class Odd [V[_],W[_],A] (
next: M[Pr[V,W]#T, Pr[W,W]#T, A]
) extends M[V,W,A]

type Empty[A] = Unit
type Id[A] = A
type Matrix[A] = M[Empty,Id,A]

anks!
league@contrapunctus.net
@chrisleague

github.com/league/ slidesha.re/eREMXZ
scala-fun-patterns
Danvy, Olivier. “Functional Unparsing” J. Functional
Programming (), .
Okasaki, Chris. “From Fast Exponentiation to Square
Matrices: An Adventure in Types” Int’l Conf. Functional
Programming, .

Scala Functional Patterns

More Related Content

What's hot

Viewers also liked

Similar to Scala Functional Patterns

Recently uploaded

Scala Functional Patterns