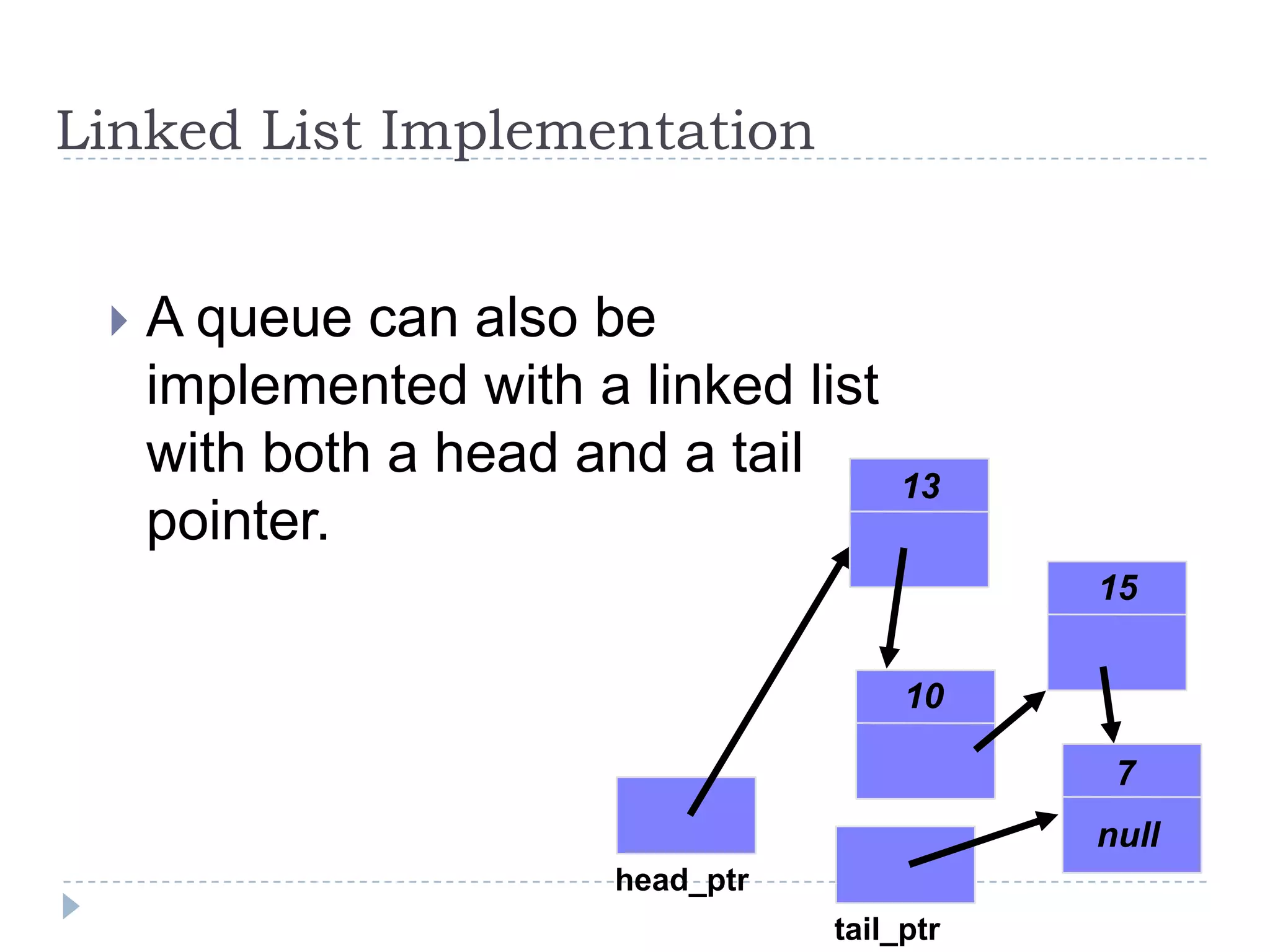
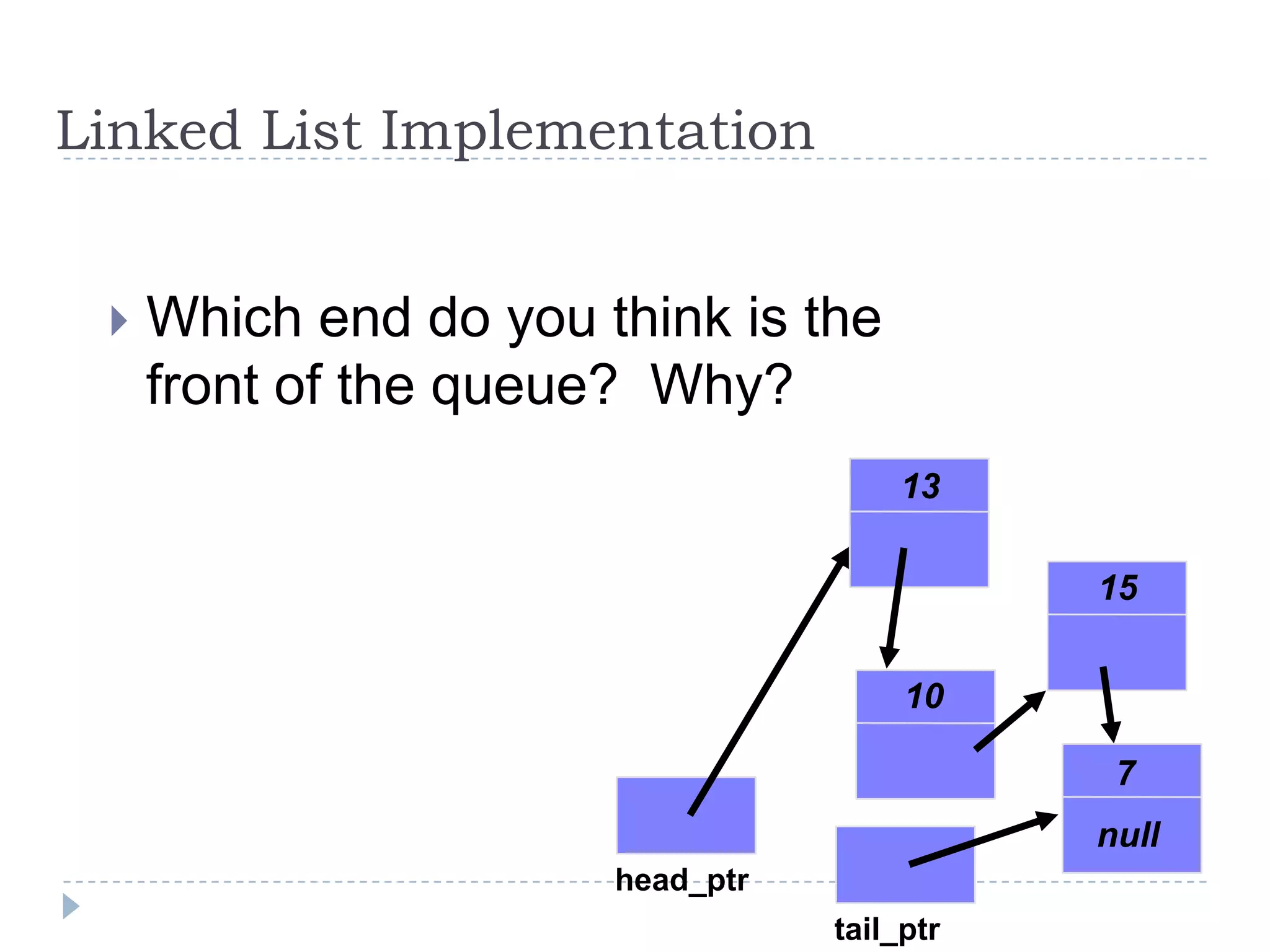
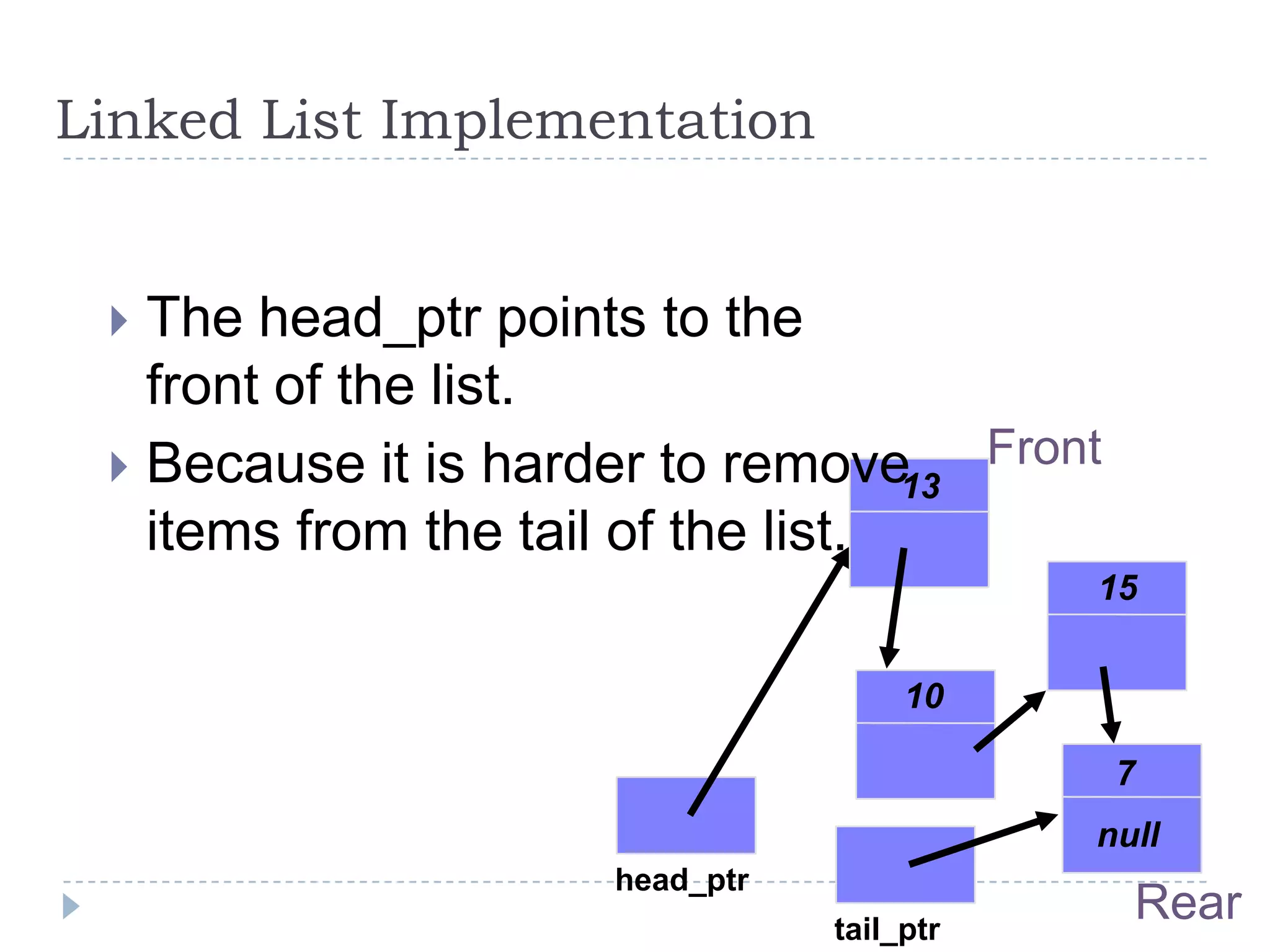
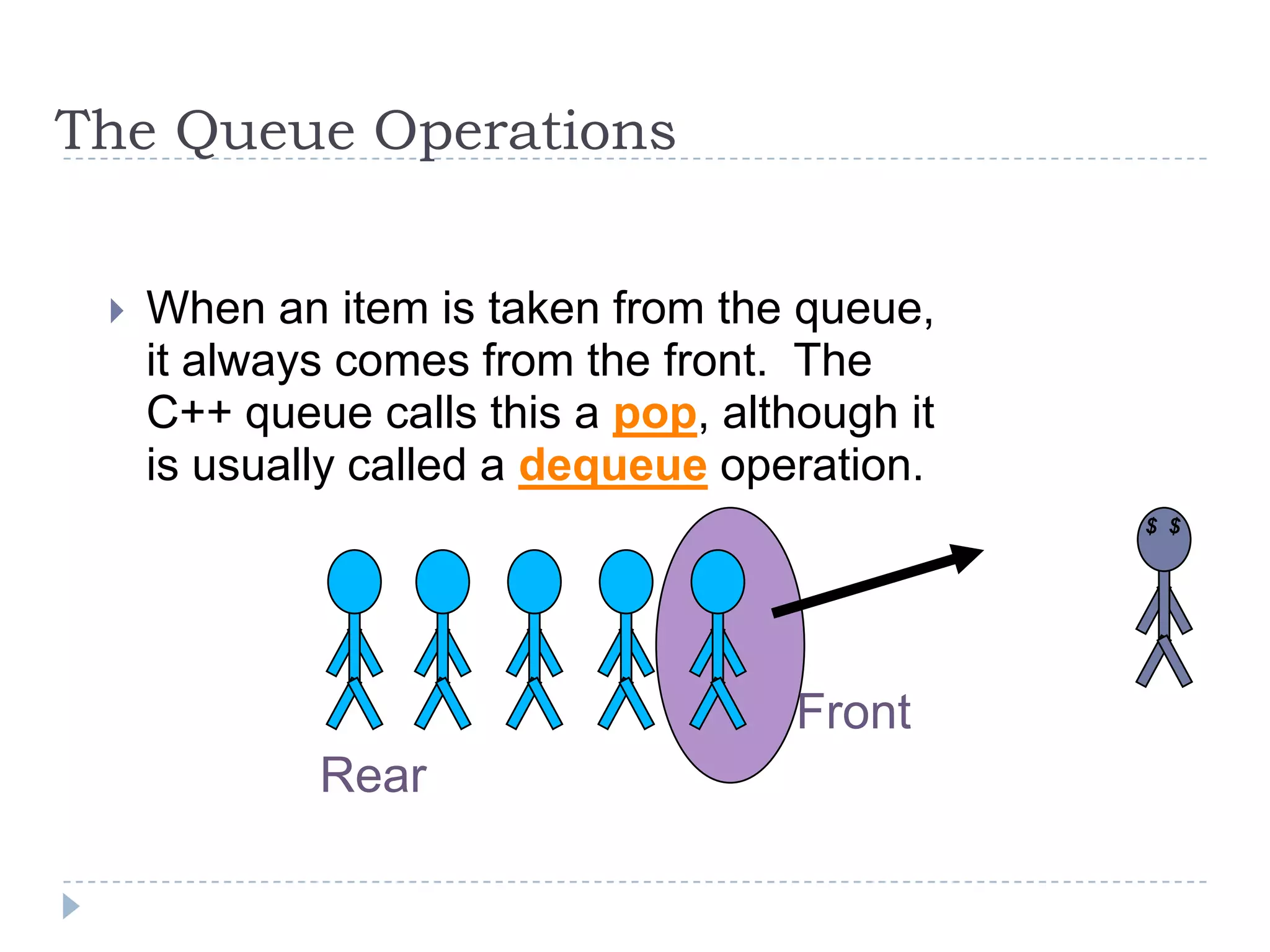
A queue is a data structure that follows the first-in, first-out (FIFO) principle. Elements are added to the rear of the queue and removed from the front. A queue can be implemented using an array, with indexes to track the front and rear elements. When an element is added (enqueued), the rear index is incremented; when an element is removed (dequeued), the front index is incremented and the element at that index is returned. The queue has a limited capacity based on the size of the array.






![Stack Implementation
#include <stdio.h>
#include<conio.h>
# define MAXSIZE 200
int stack[MAXSIZE];
int top; //index pointing to the top of stack
void main()
{
void push(int);
int pop();
int will=1,i,num;
clrscr();
while(will ==1)
{
printf(" MAIN MENU:n 1.Add element to stackn2.Delete element from the stack");
scanf("%d",&will);
8 Chapter 5: Stacks](https://image.slidesharecdn.com/u3-stackqueue-111024104210-phpapp02/75/U3-stack-queue-8-2048.jpg)

![ void push(int y)
{
if(top>MAXSIZE)
{
printf("nSTACK FULL");
return;
}
else
{
top++;
stack[top]=y;
}
}
10 Chapter 5: Stacks](https://image.slidesharecdn.com/u3-stackqueue-111024104210-phpapp02/75/U3-stack-queue-10-2048.jpg)
![ int pop()
{
int a;
if(top<=0)
{
printf("STACK EMPTY ");
return 0;
}
else
{
a=stack[top];
top--;
}
return(a);
}
11 Chapter 5: Stacks](https://image.slidesharecdn.com/u3-stackqueue-111024104210-phpapp02/75/U3-stack-queue-11-2048.jpg)












![Array Implementation
A queue can be implemented with an array, as
shown here. For example, this queue contains
the integers 4 (at the front), 8 and 6 (at the rear).
[0] [1] [2] [3] [4] [5] ...
4 8 6
An array of
integers to
implement a We don't care what's in
queue of integers this part of the array.](https://image.slidesharecdn.com/u3-stackqueue-111024104210-phpapp02/75/U3-stack-queue-32-2048.jpg)
![Array Implementation
The easiest implementation also 3 size
keeps track of the number of items in
the queue and the index of the first first
0
element (at the front of the queue),
the last element (at the rear).
2 last
[0] [1] [2] [3] [4] [5] ...
4 8 6](https://image.slidesharecdn.com/u3-stackqueue-111024104210-phpapp02/75/U3-stack-queue-33-2048.jpg)
![A Dequeue Operation
When an element leaves the queue, 2 size
size is decremented, and first
changes, too. first
1
2 last
[0] [1] [2] [3] [4] [5] ...
4 8 6](https://image.slidesharecdn.com/u3-stackqueue-111024104210-phpapp02/75/U3-stack-queue-34-2048.jpg)
![An Enqueue Operation
When an element enters the queue, 3 size
size is incremented, and last
changes, too. first
1
3 last
[0] [1] [2] [3] [4] [5] ...
8 6 2](https://image.slidesharecdn.com/u3-stackqueue-111024104210-phpapp02/75/U3-stack-queue-35-2048.jpg)
![At the End of the Array
There is special behavior at the end 3 size
of the array. For example, suppose
we want to add a new element to this first
3
queue, where the last index is [5]:
5 last
[0] [1] [2] [3] [4] [5]
2 6 1](https://image.slidesharecdn.com/u3-stackqueue-111024104210-phpapp02/75/U3-stack-queue-36-2048.jpg)
![At the End of the Array
The new element goes at the front of 4 size
the array (if that spot isn’t already
used): first
3
0 last
[0] [1] [2] [3] [4] [5]
4 2 6 1](https://image.slidesharecdn.com/u3-stackqueue-111024104210-phpapp02/75/U3-stack-queue-37-2048.jpg)
![Array Implementation
Easy to implement 3 size
But it has a limited capacity with a fixed array
Or you must use a dynamic array for an 0 first
unbounded capacity
Special behavior is needed when the rear
2 last
reaches the end of the array.
[0] [1] [2] [3] [4] [5] ...
4 8 6](https://image.slidesharecdn.com/u3-stackqueue-111024104210-phpapp02/75/U3-stack-queue-38-2048.jpg)