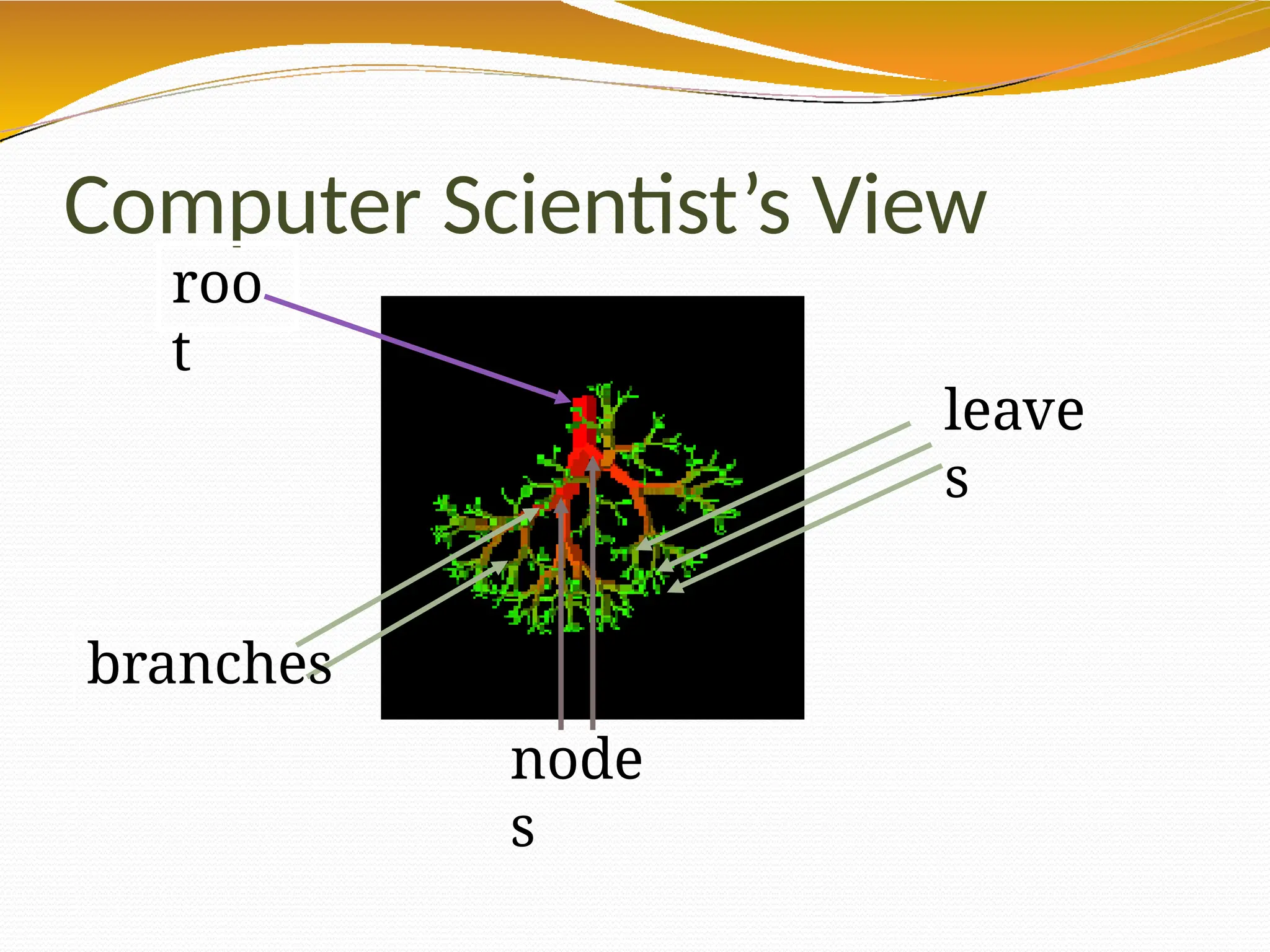
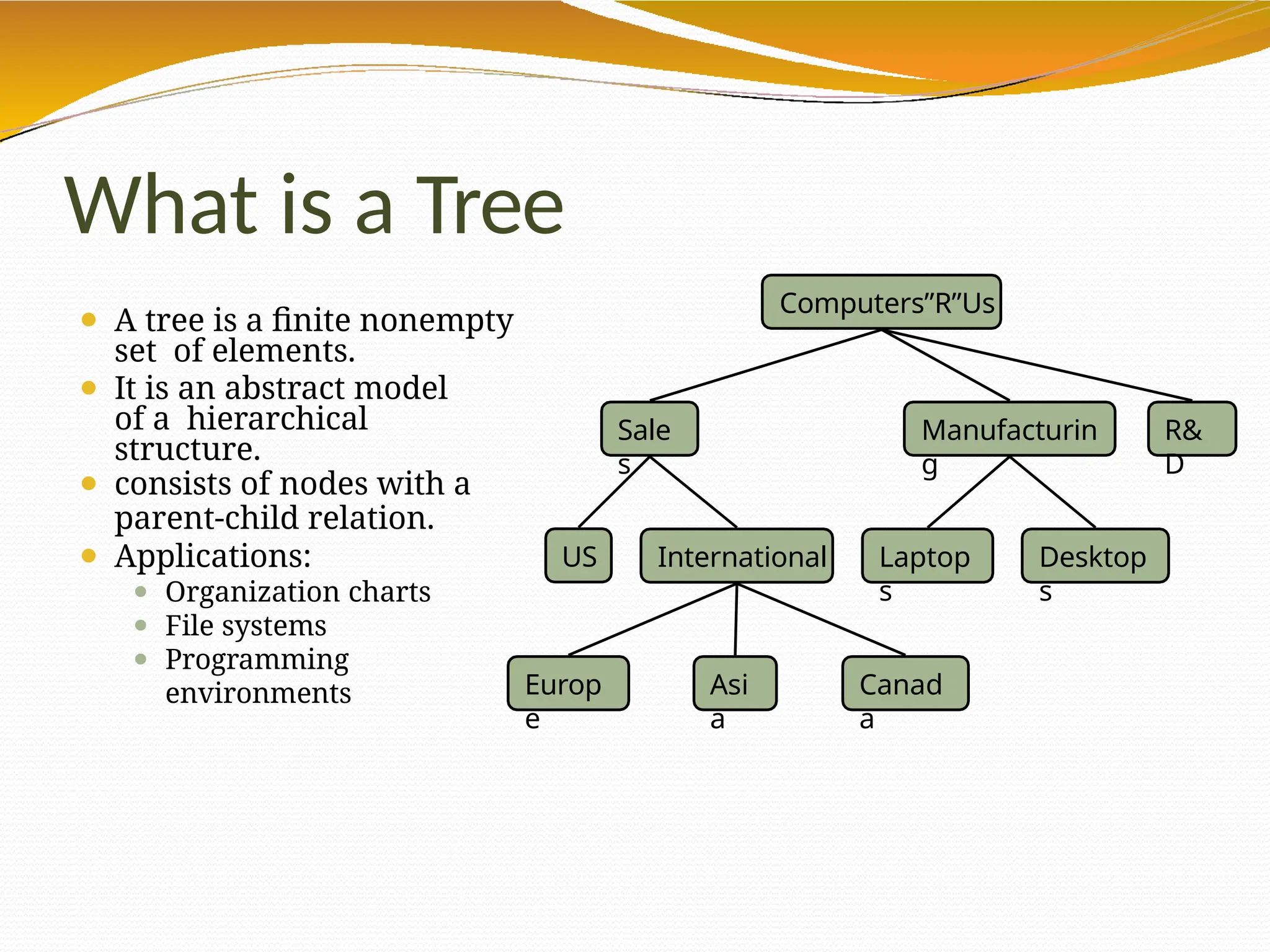
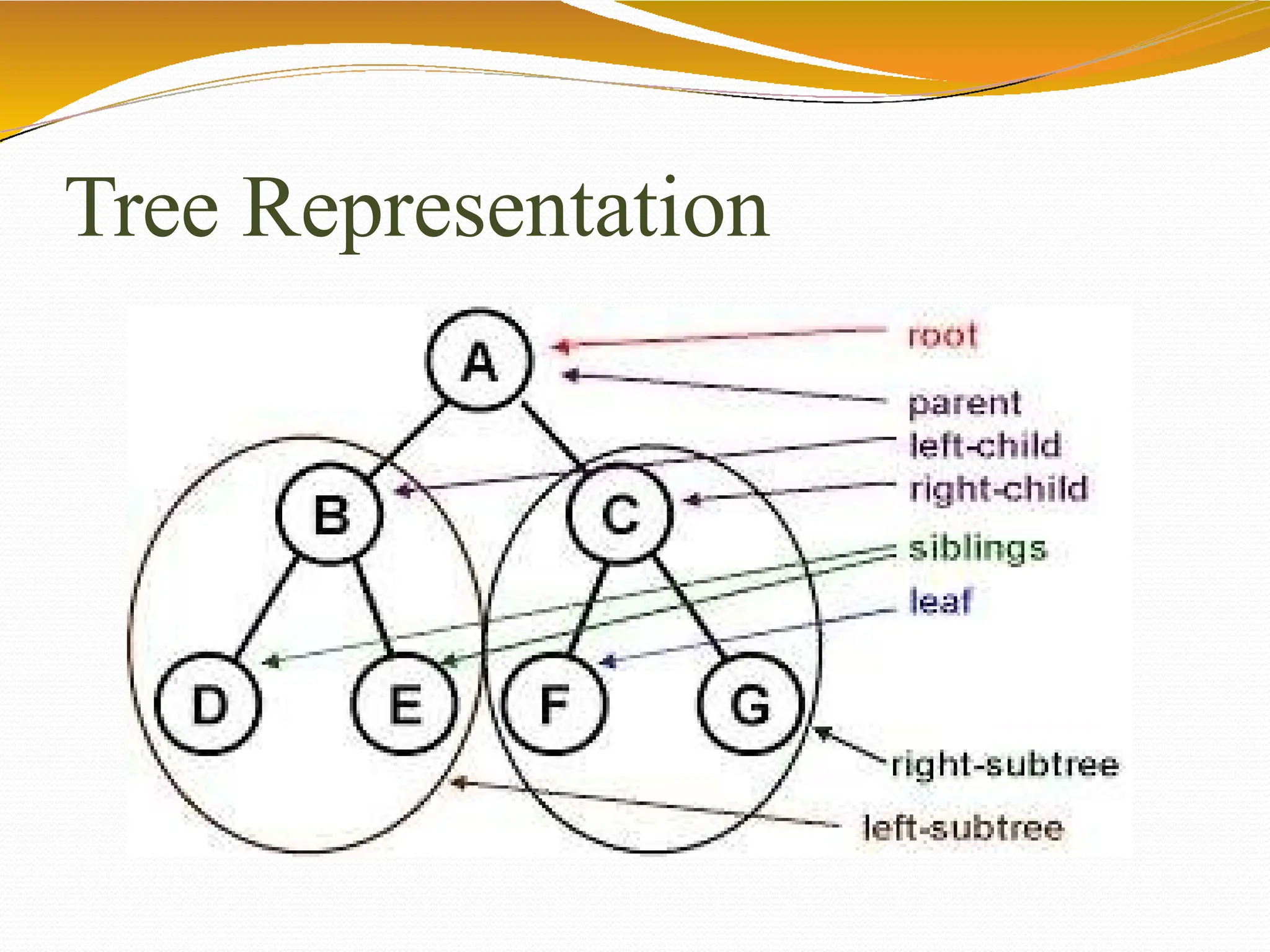
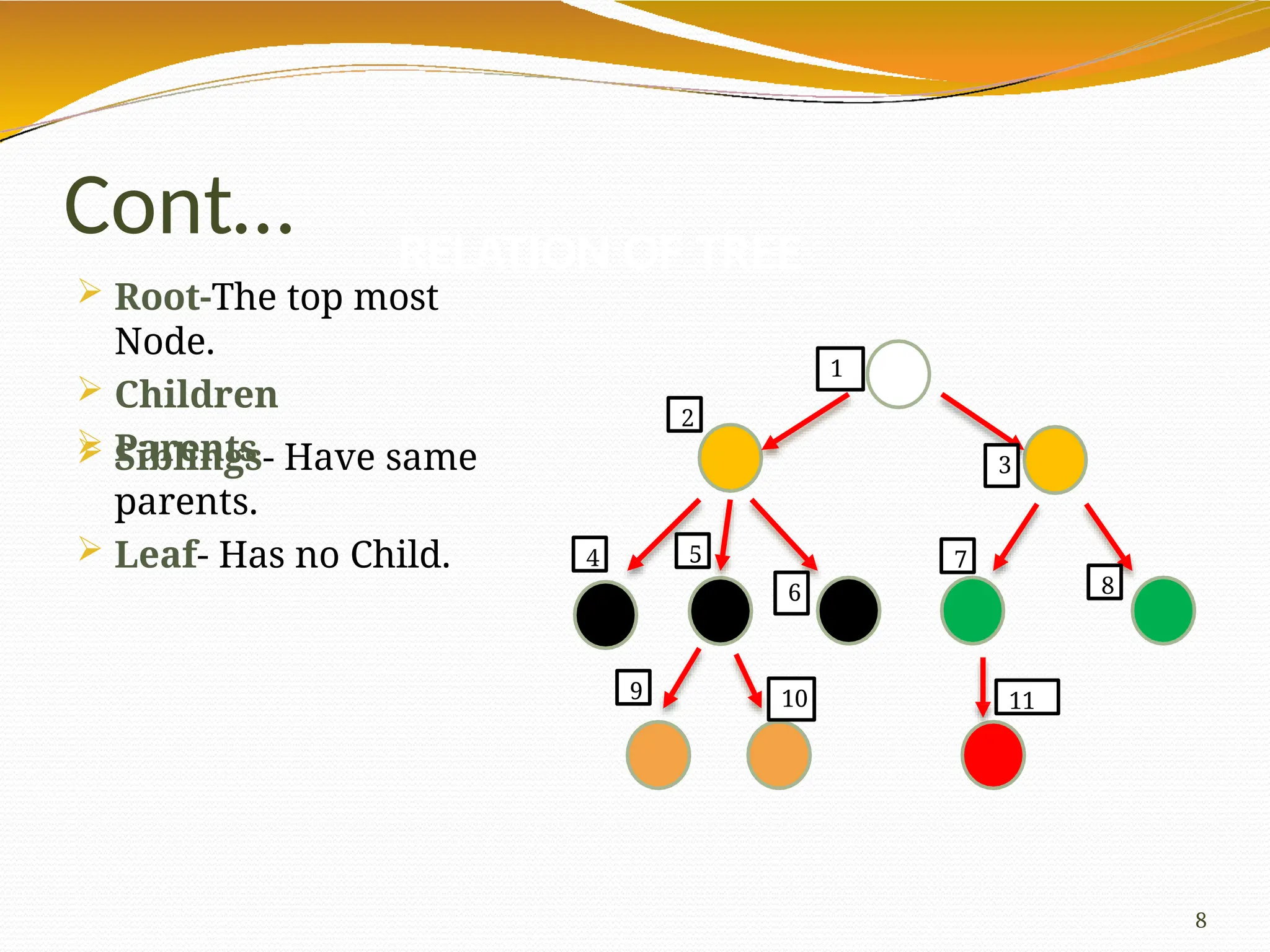
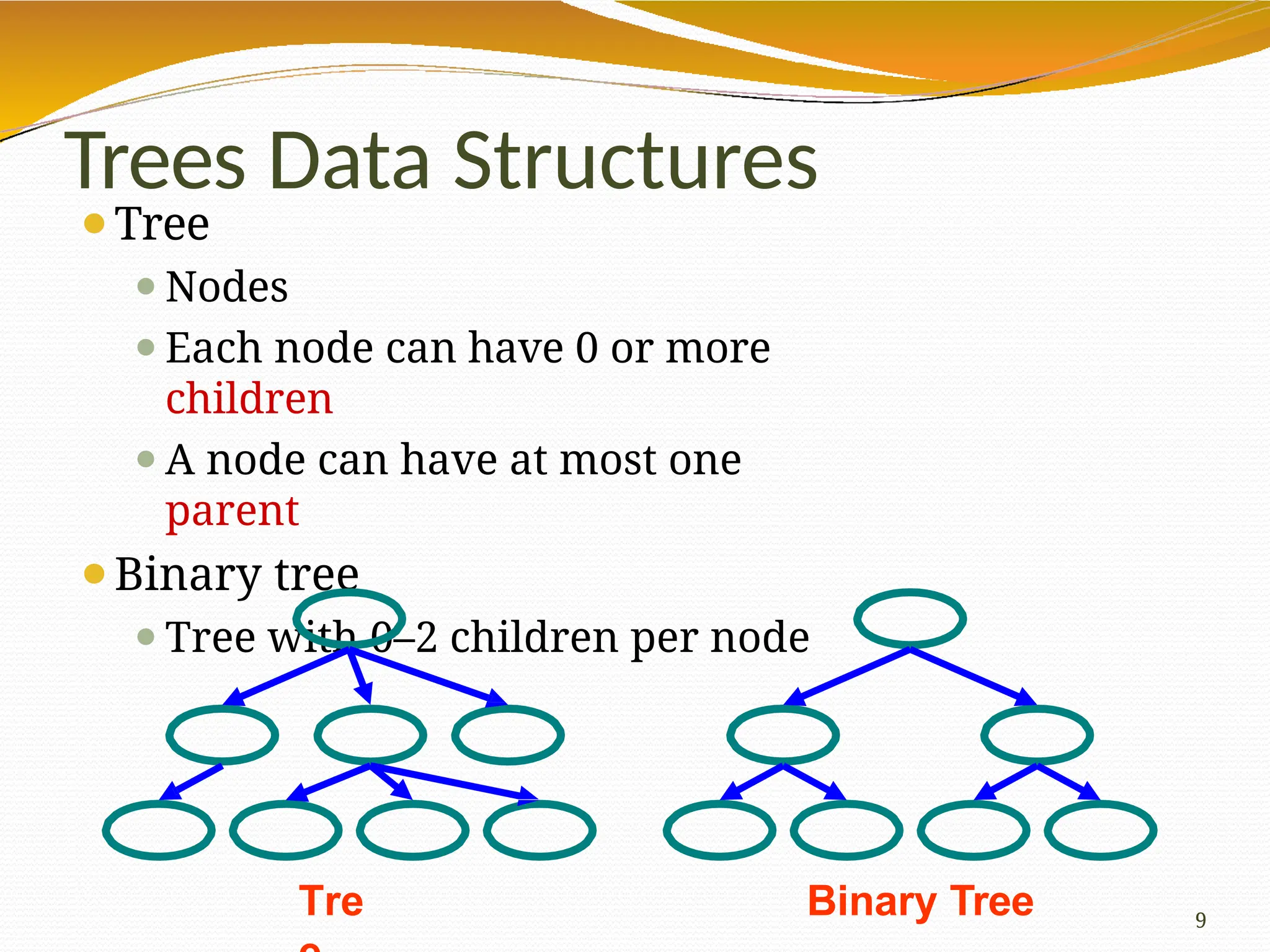
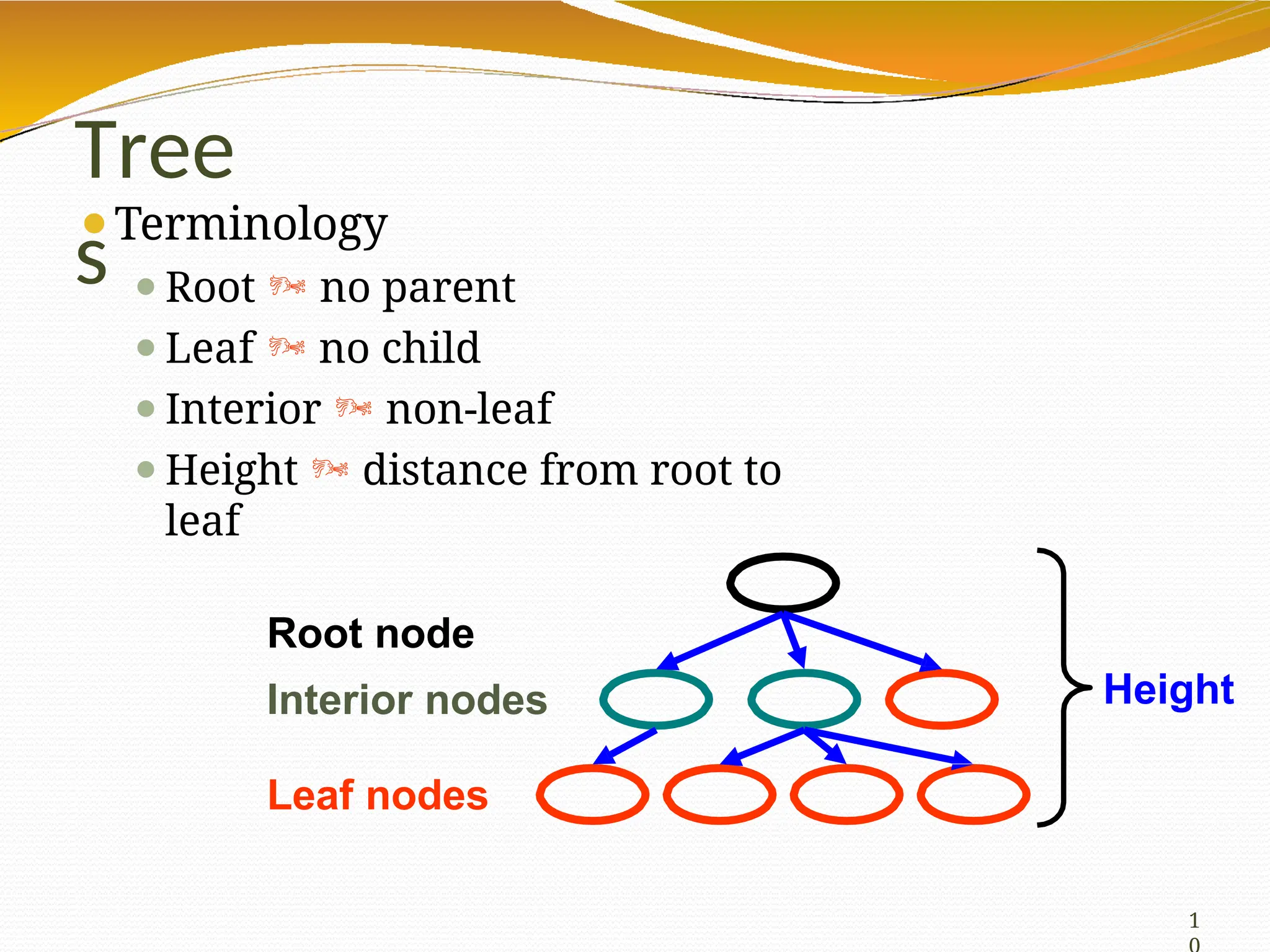
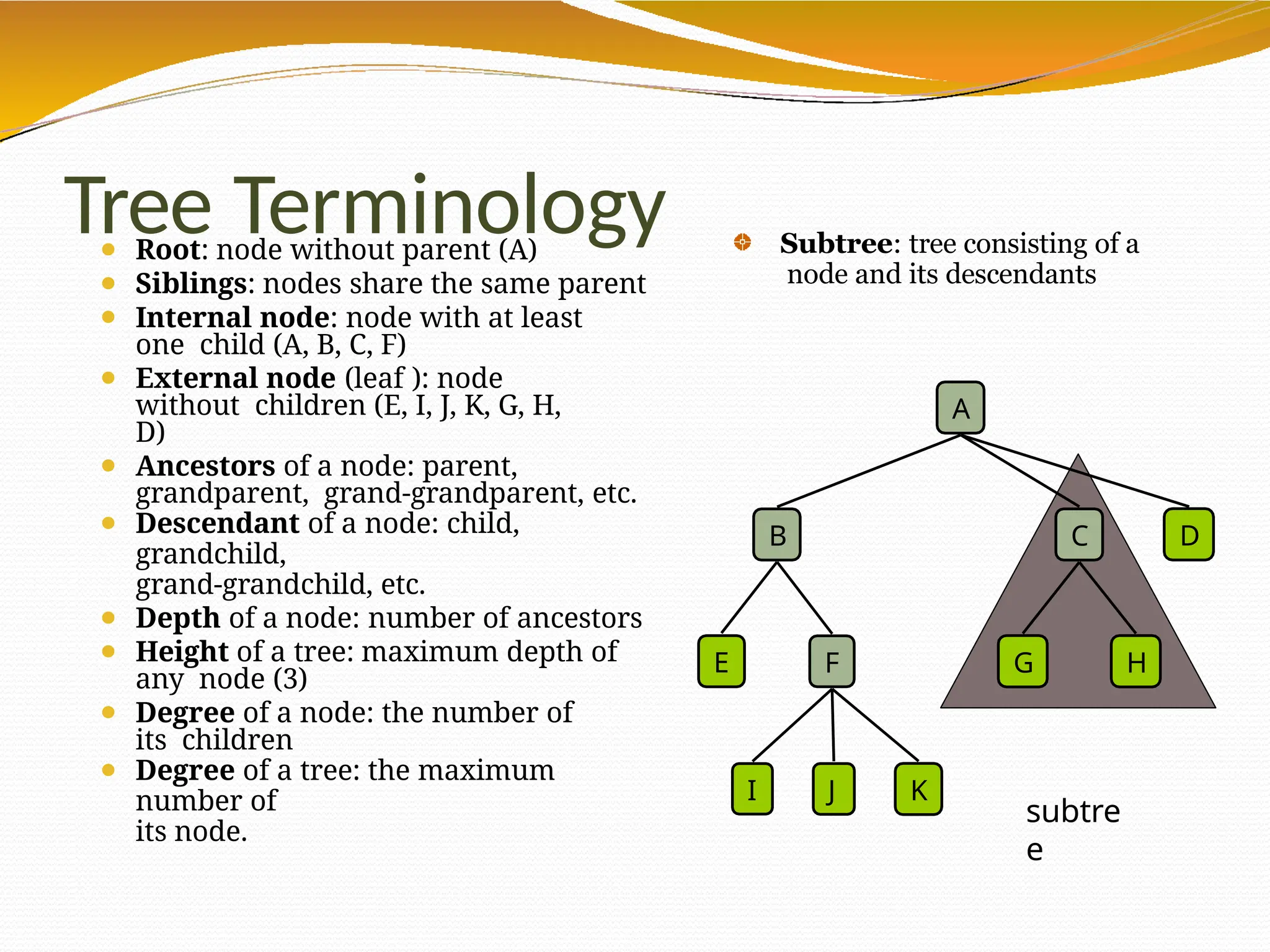
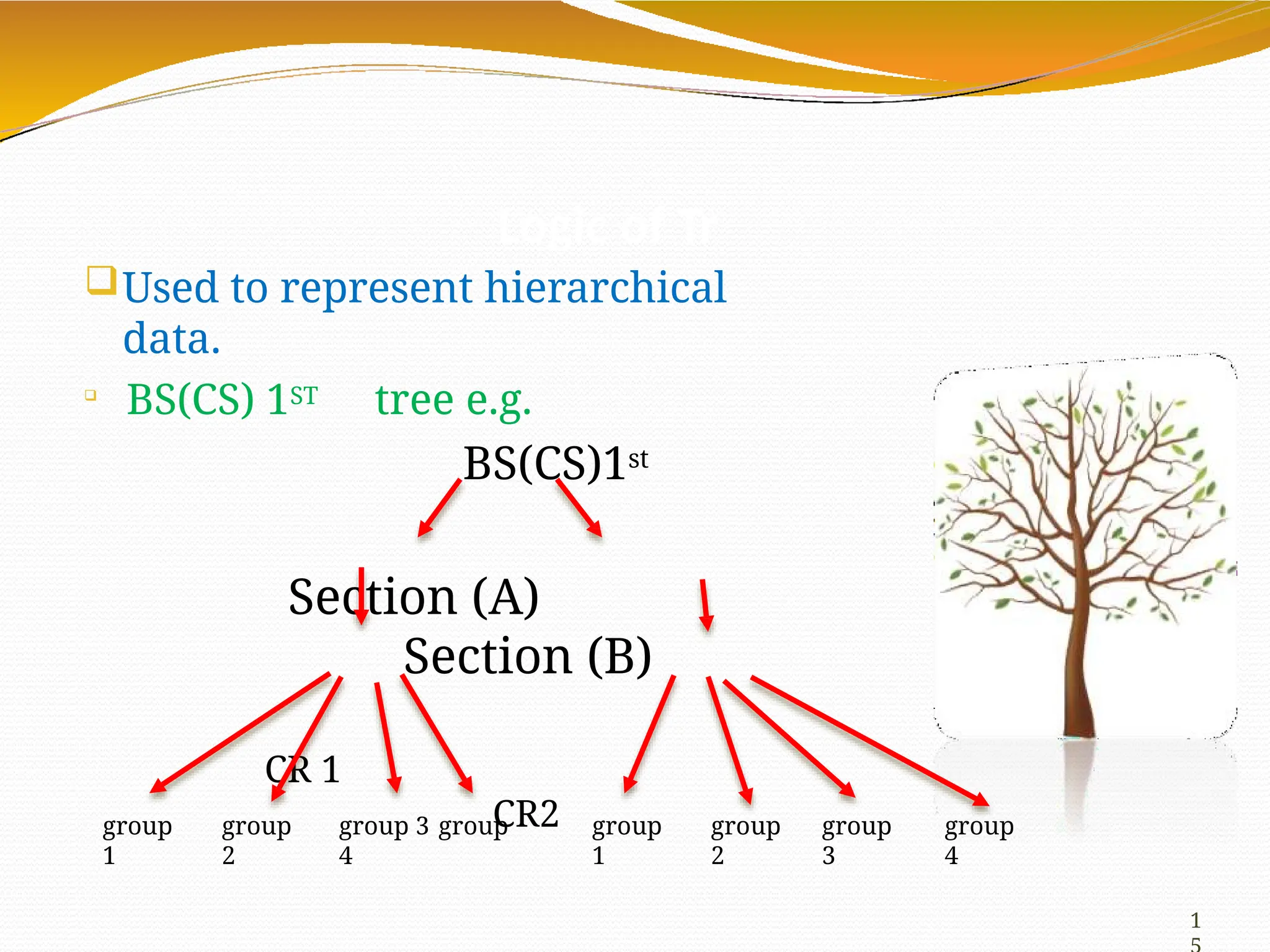
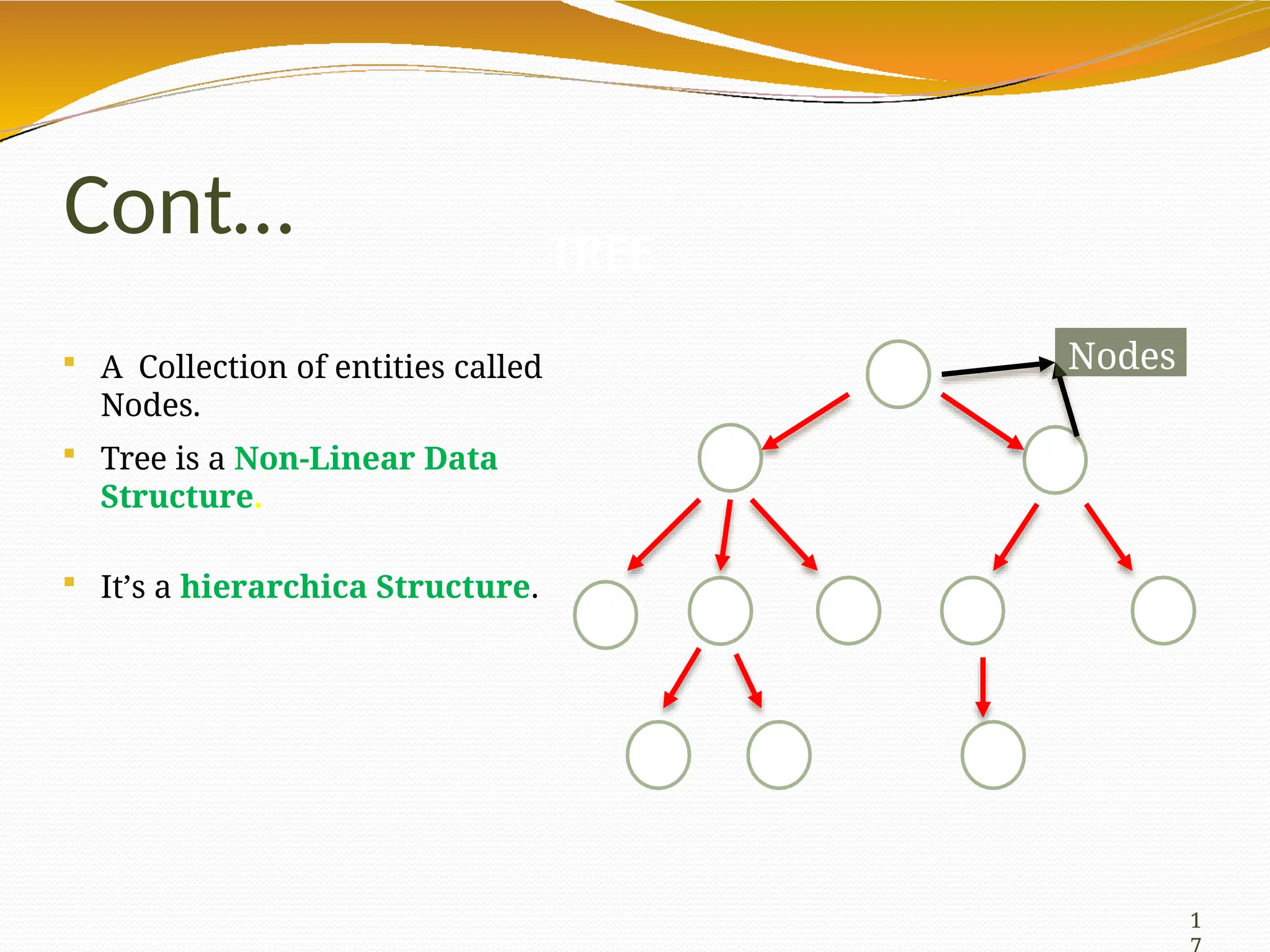
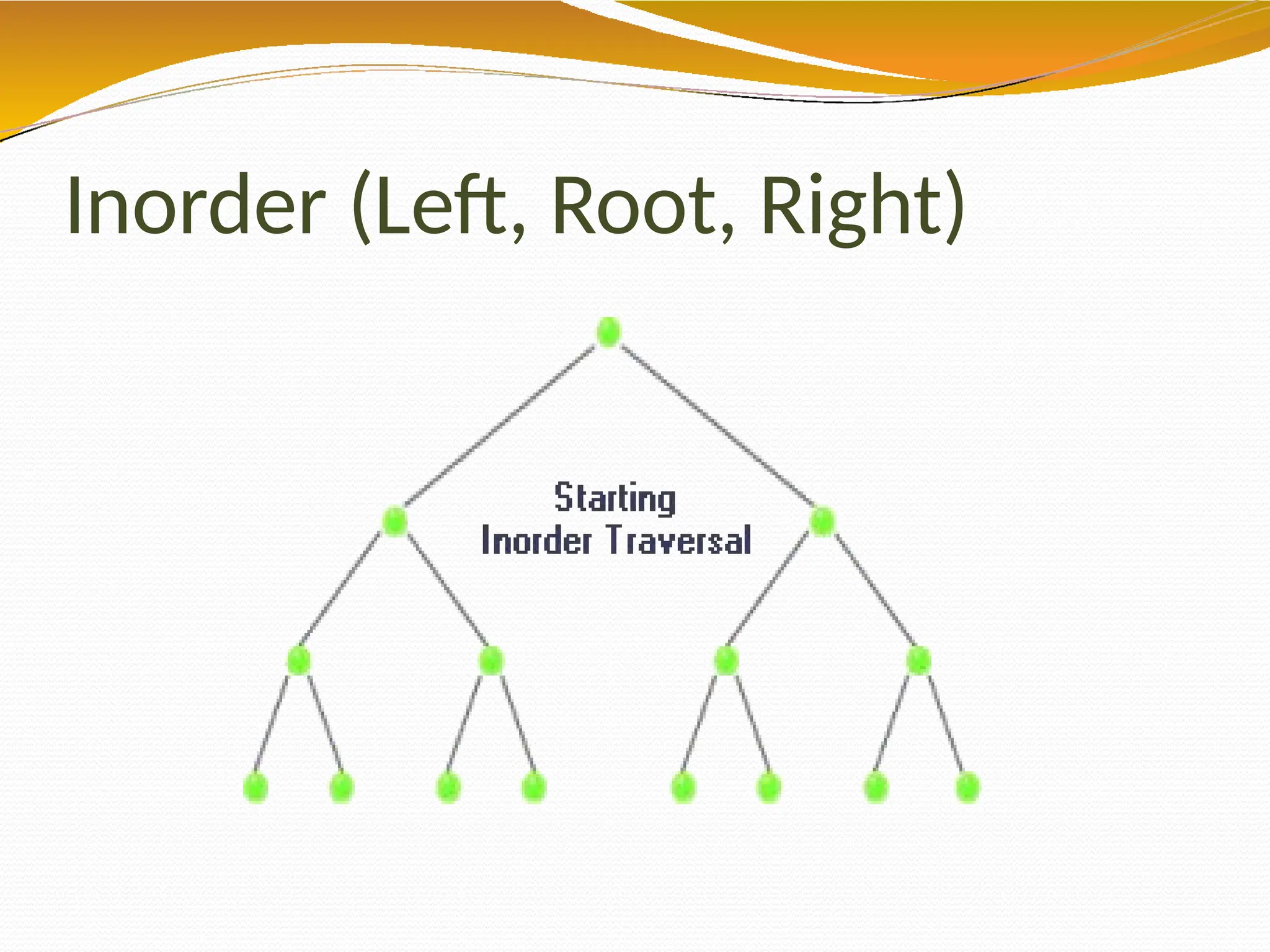
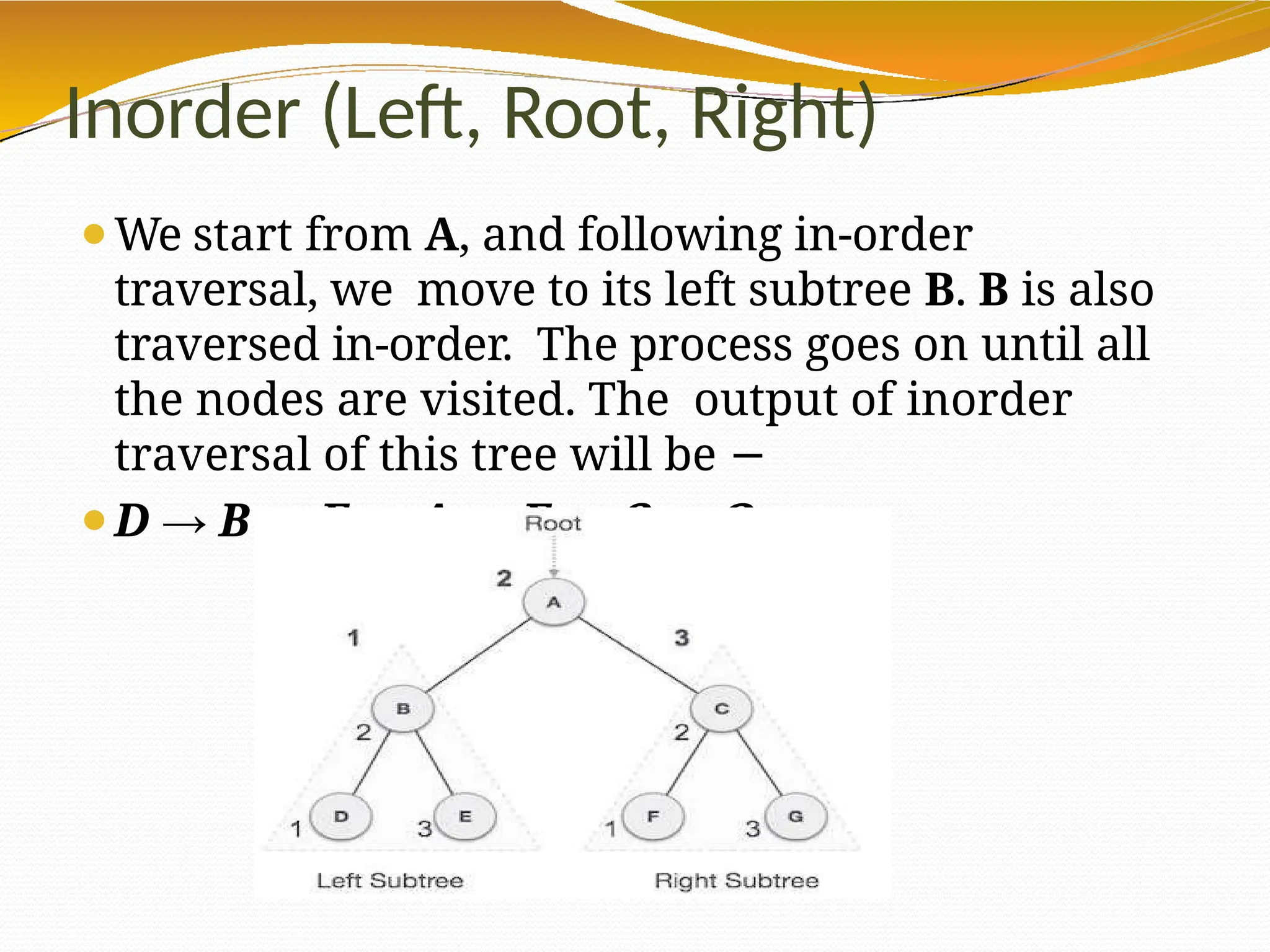
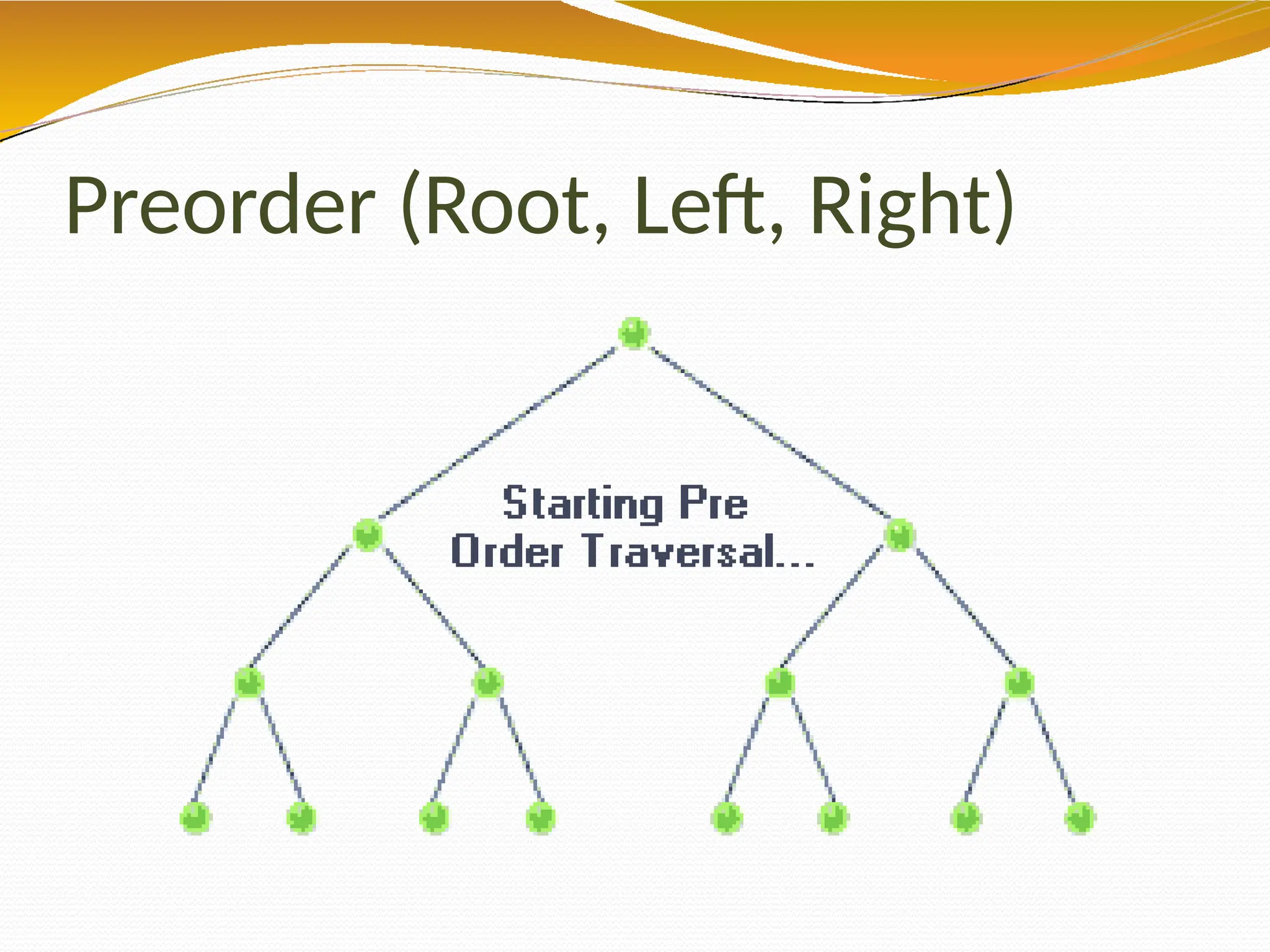
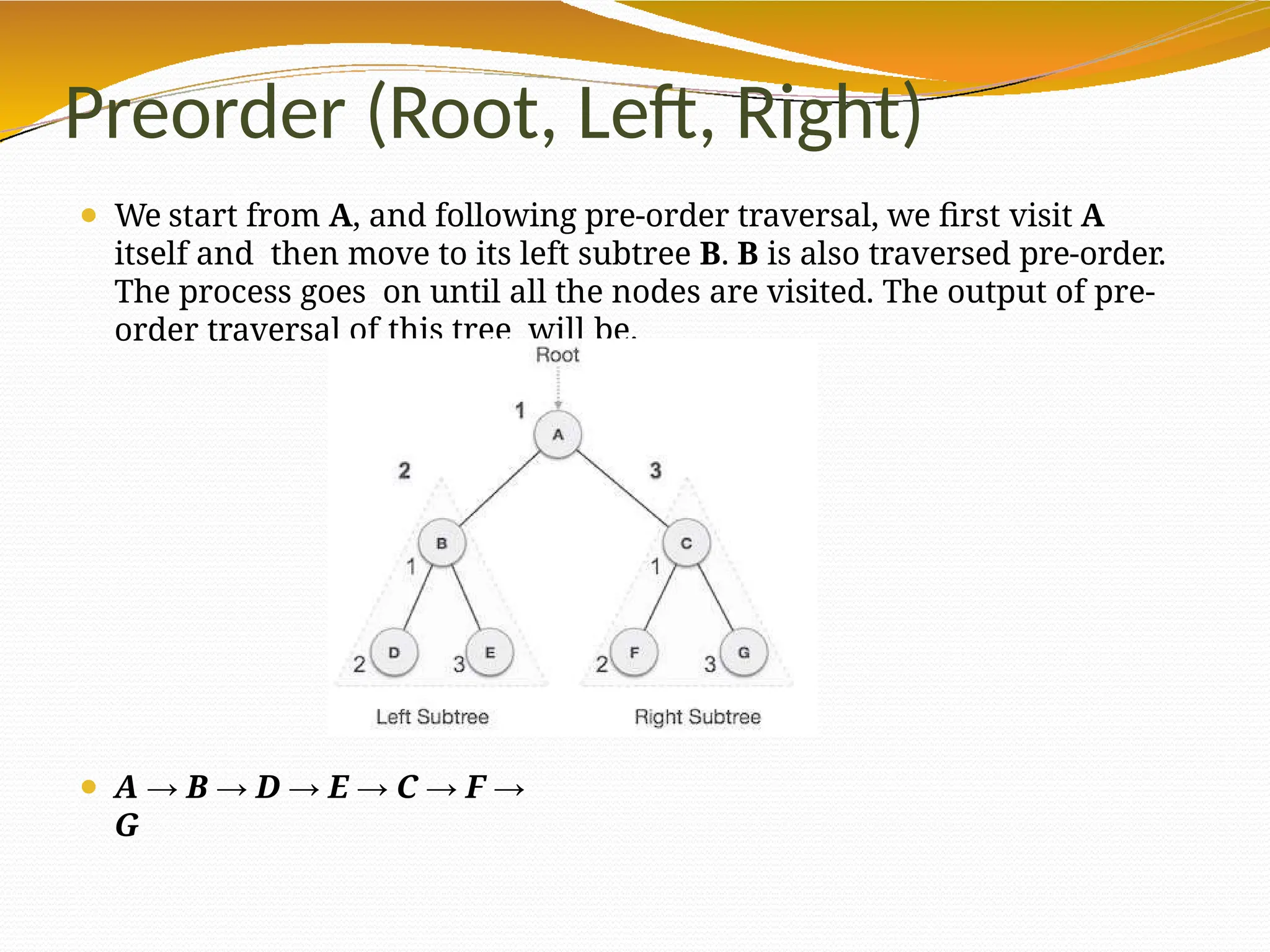
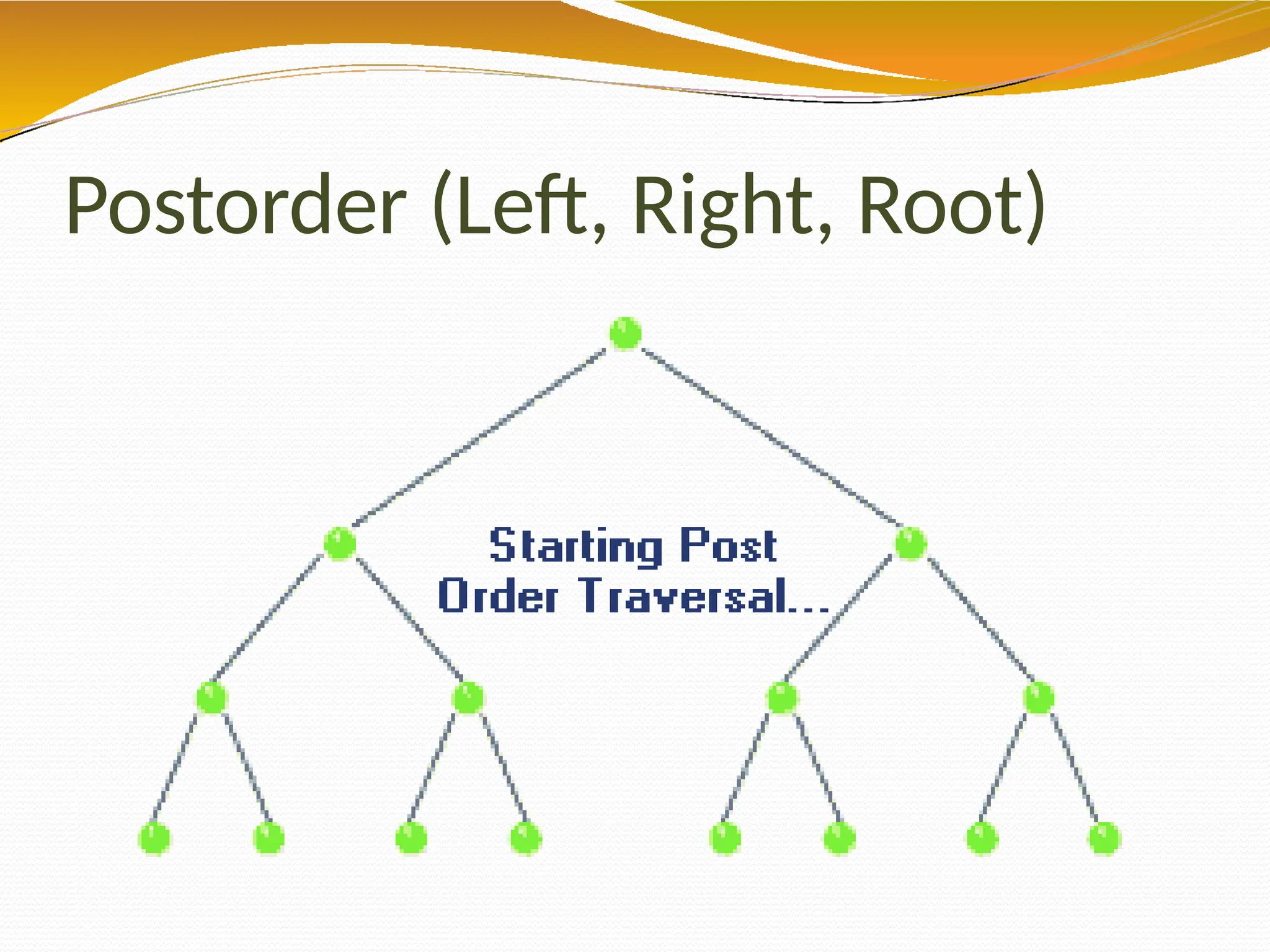
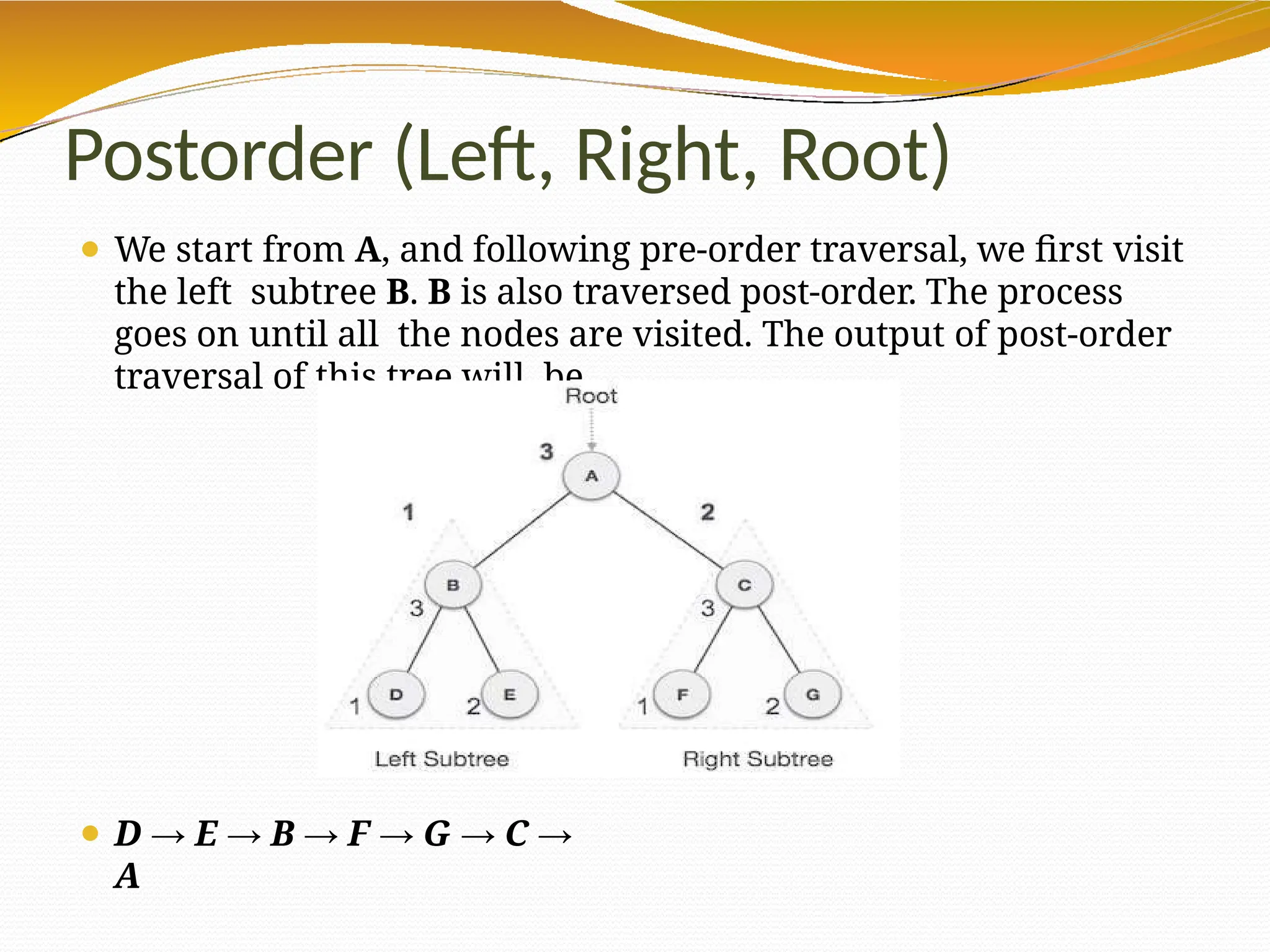
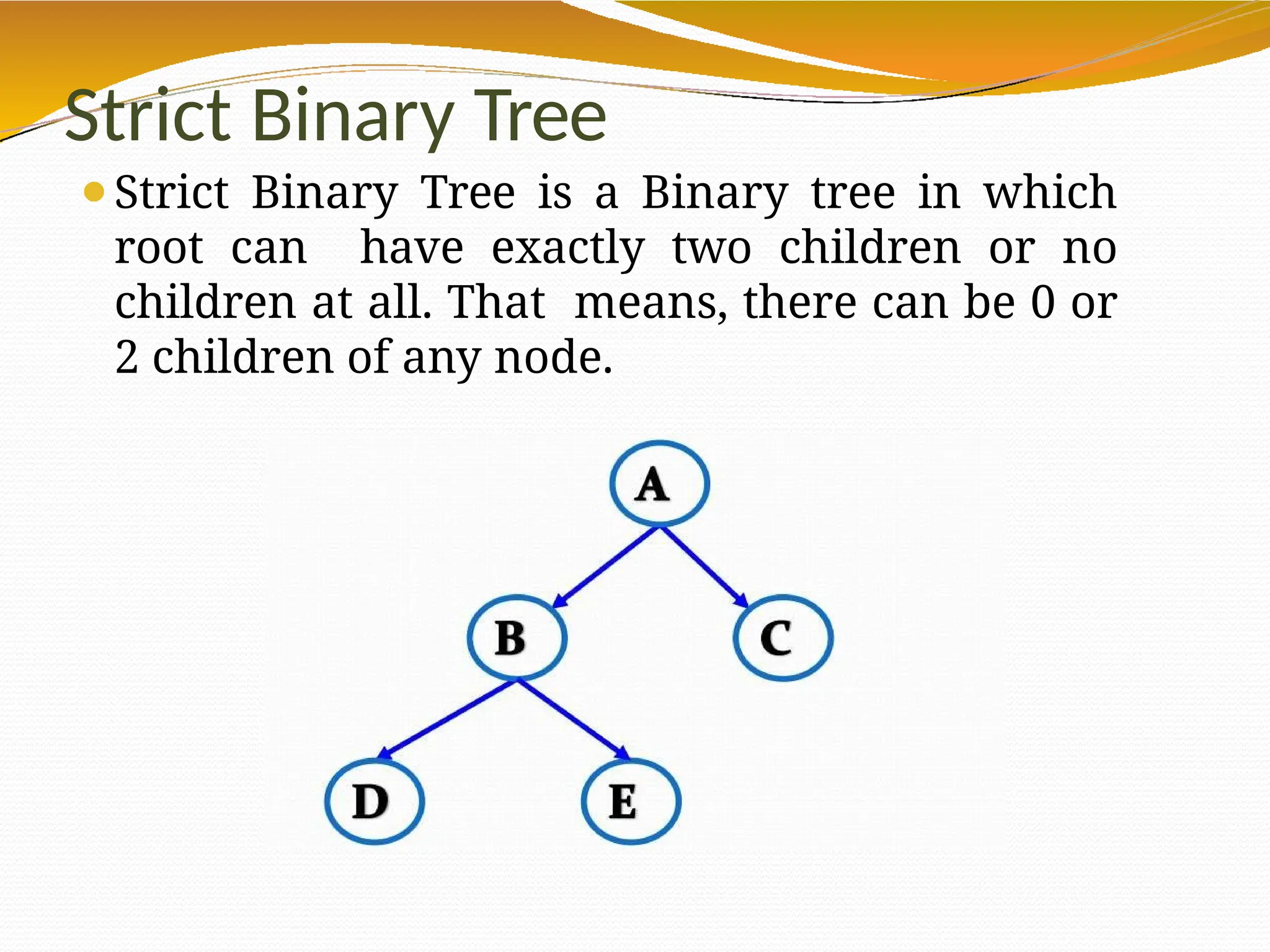
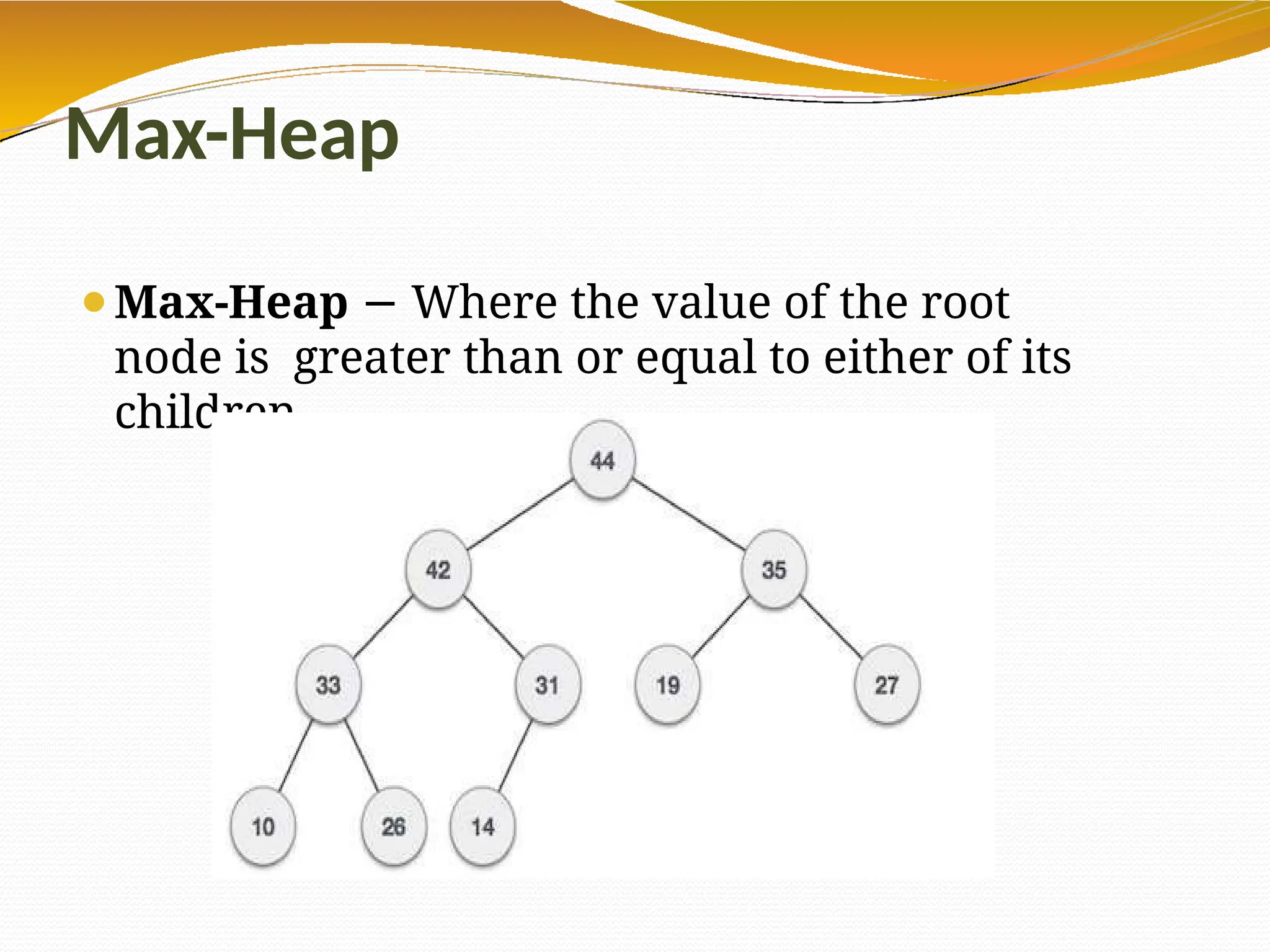
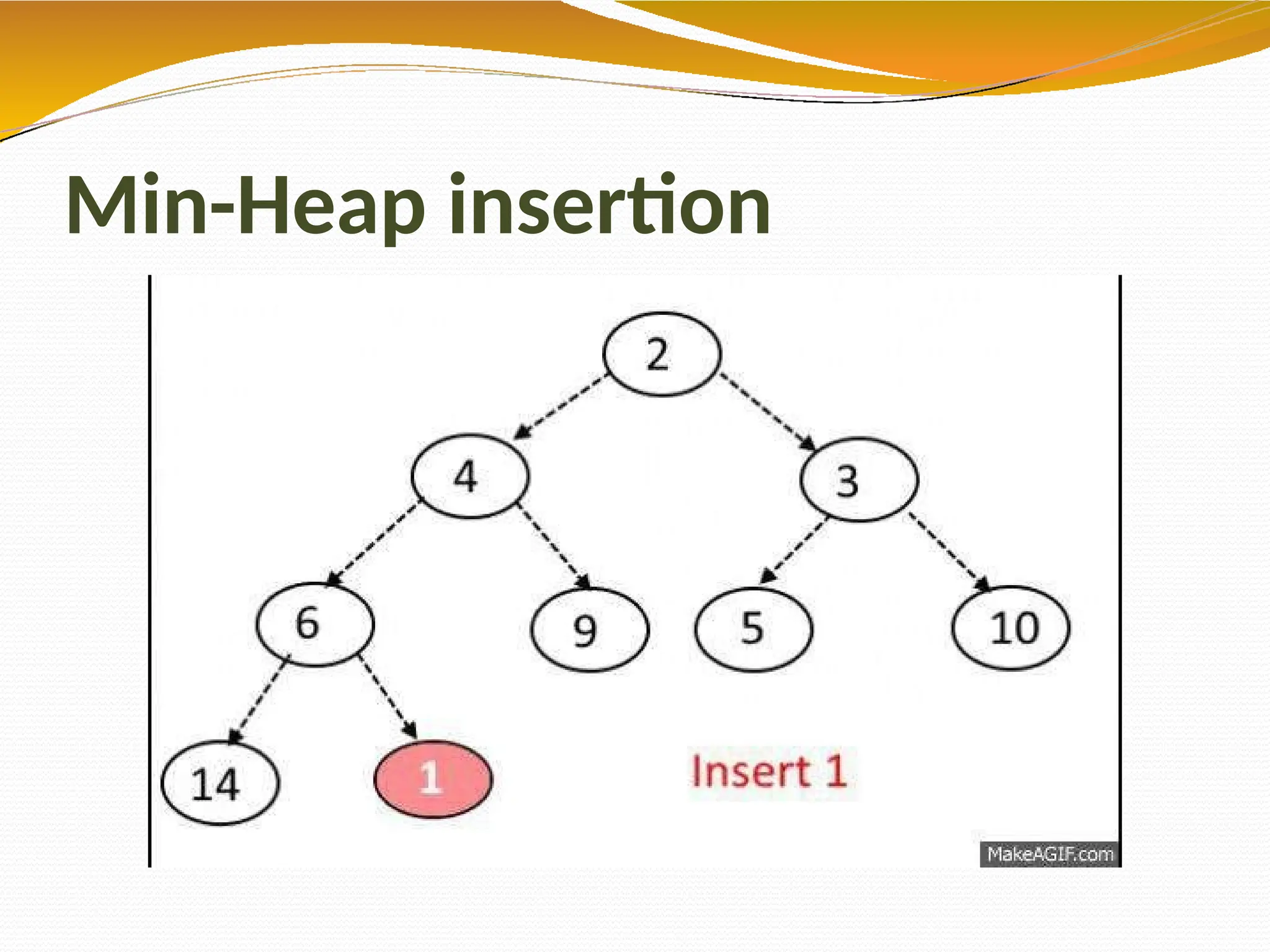
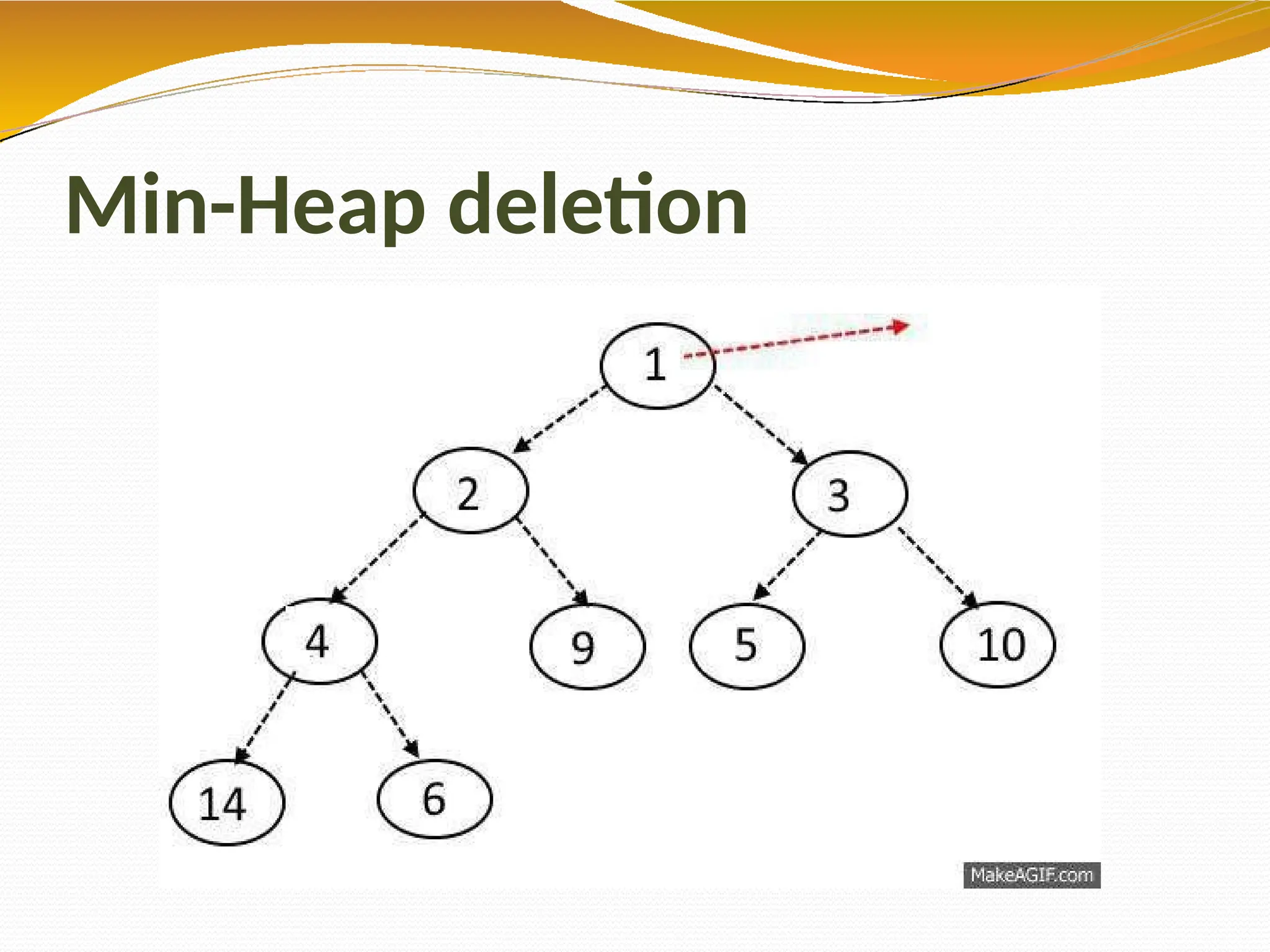
The document provides an overview of tree data structures in computer science, explaining their hierarchical nature, terminology, and various types such as binary trees, B-trees, and heaps. It discusses key concepts including traversals (in-order, pre-order, post-order), node relationships (root, parent, child, leaf), and operations like insertion, deletion, and searching. Additionally, it emphasizes the significance of trees in organizing data and their applications in real-world scenarios.