0% found this document useful (0 votes)
90 views5 pagesQuadratic Functions Quiz
I. The document contains a math quiz on quadratic functions with multiple parts:
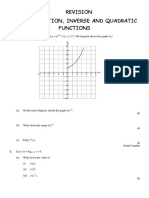
1) Find the vertex of f(x) = 2x^2 - 4x - 6.
2) Sketch the graph of f showing x and y intercepts.
3) Consider the function g(x) = x^2. Find values of k, p, and q such that the graph of f can be obtained from g through a vertical stretch by k and a translation by the vector (p, q).
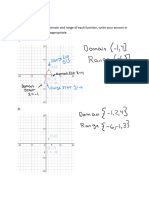
II. Let f(x) = 2x^2 - 3 and g(x) = x + a.
1) Write the equation of h(x) =
Uploaded by
ibrahim fadelCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
90 views5 pagesQuadratic Functions Quiz
I. The document contains a math quiz on quadratic functions with multiple parts:
1) Find the vertex of f(x) = 2x^2 - 4x - 6.
2) Sketch the graph of f showing x and y intercepts.
3) Consider the function g(x) = x^2. Find values of k, p, and q such that the graph of f can be obtained from g through a vertical stretch by k and a translation by the vector (p, q).
II. Let f(x) = 2x^2 - 3 and g(x) = x + a.
1) Write the equation of h(x) =
Uploaded by
ibrahim fadelCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 5