0% found this document useful (0 votes)
74 views45 pagesEfficient AM Systems for Engineers
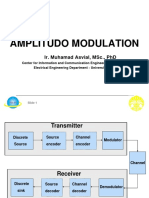
The document describes DSBSC-AM (double sideband suppressed carrier amplitude modulation). It discusses the time domain representation and mathematical expressions for a DSBSC-AM wave. It also covers the generation of a DSBSC-AM wave using a balanced modulator circuit. Key points are that in DSBSC-AM, the carrier is suppressed, reducing transmitted power compared to DSBFC-AM while maintaining the same bandwidth of 2fm. A balanced modulator can generate a DSBSC-AM wave by mixing the modulating signal with the carrier signal in a balanced nonlinear circuit.
Uploaded by
gkCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
74 views45 pagesEfficient AM Systems for Engineers
The document describes DSBSC-AM (double sideband suppressed carrier amplitude modulation). It discusses the time domain representation and mathematical expressions for a DSBSC-AM wave. It also covers the generation of a DSBSC-AM wave using a balanced modulator circuit. Key points are that in DSBSC-AM, the carrier is suppressed, reducing transmitted power compared to DSBFC-AM while maintaining the same bandwidth of 2fm. A balanced modulator can generate a DSBSC-AM wave by mixing the modulating signal with the carrier signal in a balanced nonlinear circuit.
Uploaded by
gkCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 45