0% found this document useful (0 votes)
163 views39 pagesTruss Lecture NoTES
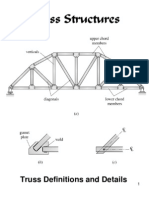
The document provides a comprehensive overview of trusses, including their definitions, classifications, assumptions for design, and methods for analysis. It explains the concepts of stability, determinacy, and the methods of joints and sections for determining member forces. Additionally, it includes examples and problems for practical application of the theoretical concepts discussed.
Uploaded by
nuha0albashir2003Copyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
163 views39 pagesTruss Lecture NoTES
The document provides a comprehensive overview of trusses, including their definitions, classifications, assumptions for design, and methods for analysis. It explains the concepts of stability, determinacy, and the methods of joints and sections for determining member forces. Additionally, it includes examples and problems for practical application of the theoretical concepts discussed.
Uploaded by
nuha0albashir2003Copyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 39