0% found this document useful (0 votes)
38 views22 pagesPlotting Mat Lab
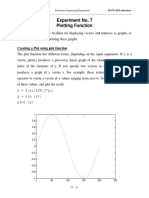
The document provides an introduction to graphing using MATLAB, focusing on the creation and formatting of line graphs. It includes examples of plotting functions, adding labels and titles, and common errors to avoid. Additionally, it covers advanced topics such as multiple plots, subplots, and saving plots.
Uploaded by
greatgakaphimiaCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
38 views22 pagesPlotting Mat Lab
The document provides an introduction to graphing using MATLAB, focusing on the creation and formatting of line graphs. It includes examples of plotting functions, adding labels and titles, and common errors to avoid. Additionally, it covers advanced topics such as multiple plots, subplots, and saving plots.
Uploaded by
greatgakaphimiaCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 22