0% found this document useful (0 votes)
158 views10 pagesSolution
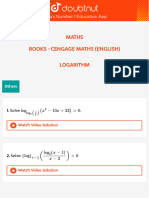
The document contains a series of mathematics questions and their corresponding answer keys, covering various topics such as equations, logarithms, and systems of equations. Each question is followed by multiple-choice options and the correct answers are provided in a separate section. Additionally, solutions to some of the problems are included, detailing the steps taken to arrive at the answers.
Uploaded by
stavya021Copyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
158 views10 pagesSolution
The document contains a series of mathematics questions and their corresponding answer keys, covering various topics such as equations, logarithms, and systems of equations. Each question is followed by multiple-choice options and the correct answers are provided in a separate section. Additionally, solutions to some of the problems are included, detailing the steps taken to arrive at the answers.
Uploaded by
stavya021Copyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 10