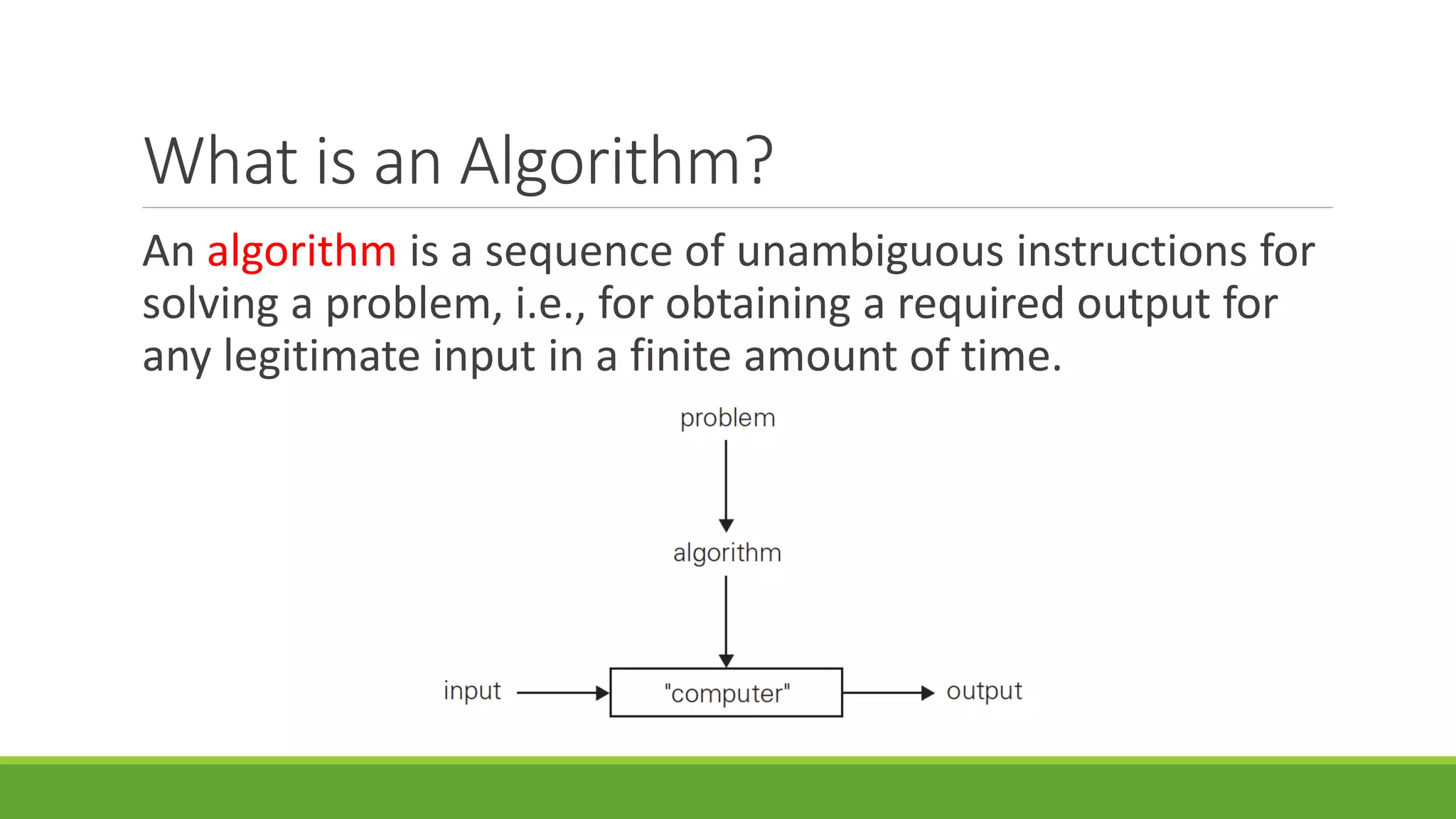
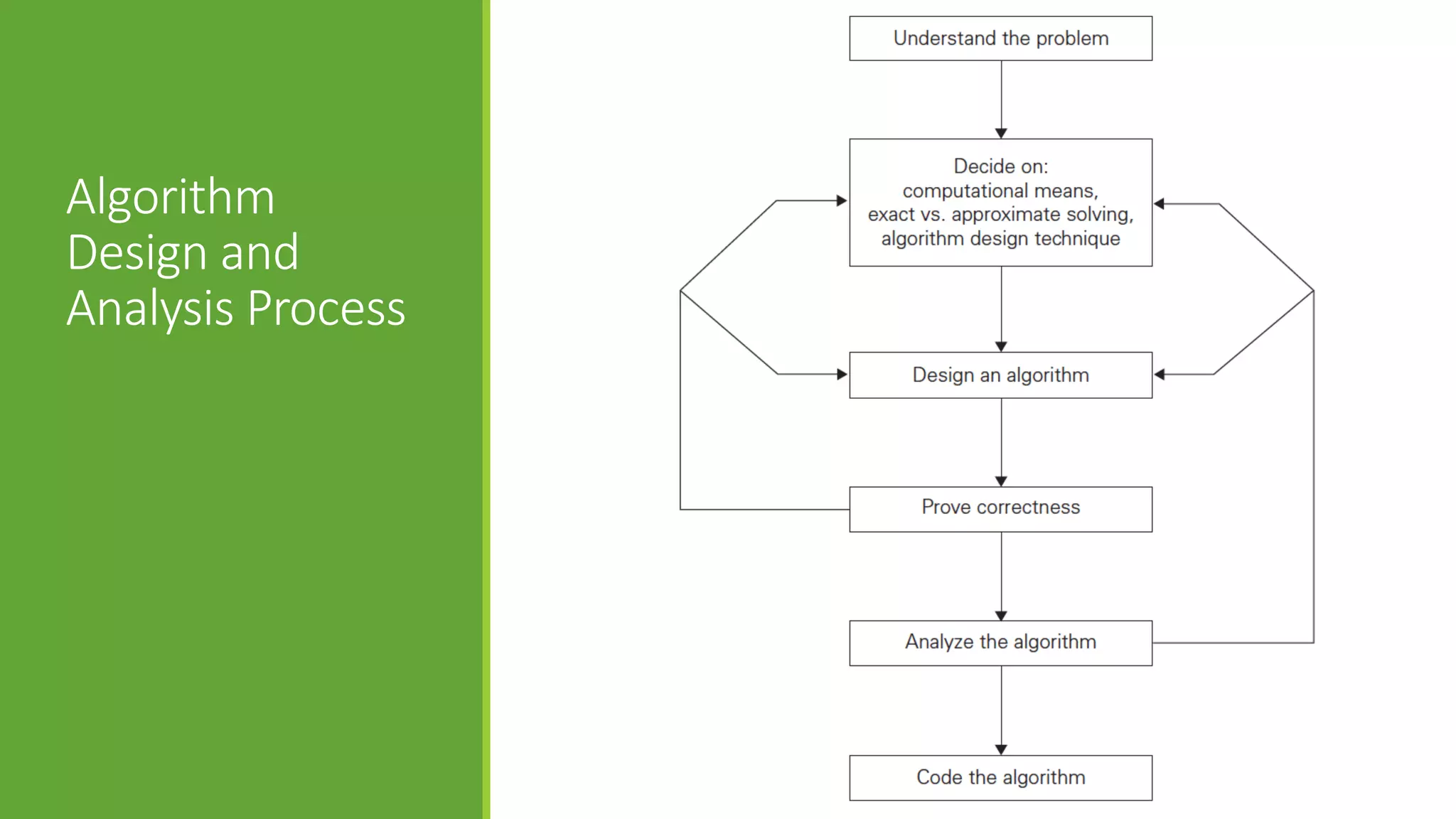
This document provides an introduction to algorithms and algorithm analysis. It defines an algorithm as a sequence of unambiguous instructions to solve a problem in a finite amount of time. The document discusses why algorithms are studied, what constitutes an algorithm, and examples of classic algorithms like Euclid's algorithm for finding the greatest common divisor and the Sieve of Eratosthenes for finding prime numbers. It also outlines the process for designing, analyzing, and implementing algorithms.