An applicative value can be seen as a value with an added context. Functional programming uses functions instead of variables. Haskell is a pure functional programming language that uses lazy evaluation, pattern matching, list comprehensions, and type polymorphism. Typeclasses define properties of types like Eq, Ord, Show, Read, and Enum. Functions can be lifted to operate on applicative types like Maybe and [] to provide context.



![Nice to remember (1)
Typeclasses:
● define properties of the types
● like an interface
– Eq can be compared
– Ord can be ordered (>, <, >=, <=) (extending Eq)
– Show can be shown as string
– Read opposite of Show
– Enum sequentially ordered types (can be enumerated
and usable in List-Ranges ['a'..'e'])](https://image.slidesharecdn.com/09-haskellcontext-130228215148-phpapp01/75/09-haskell-Context-4-2048.jpg)
![Nice to remember (2)
Typeclass-Membership:
1. derive from existing Memberships of used types
data Vector2D = Vector Float Float deriving (Show, Eq)
2. implement Membership by your own
instance Show Vector2D where
show Vector a b = “x: ” ++ [a] ++ “ ; y: ” ++ [b]](https://image.slidesharecdn.com/09-haskellcontext-130228215148-phpapp01/75/09-haskell-Context-5-2048.jpg)











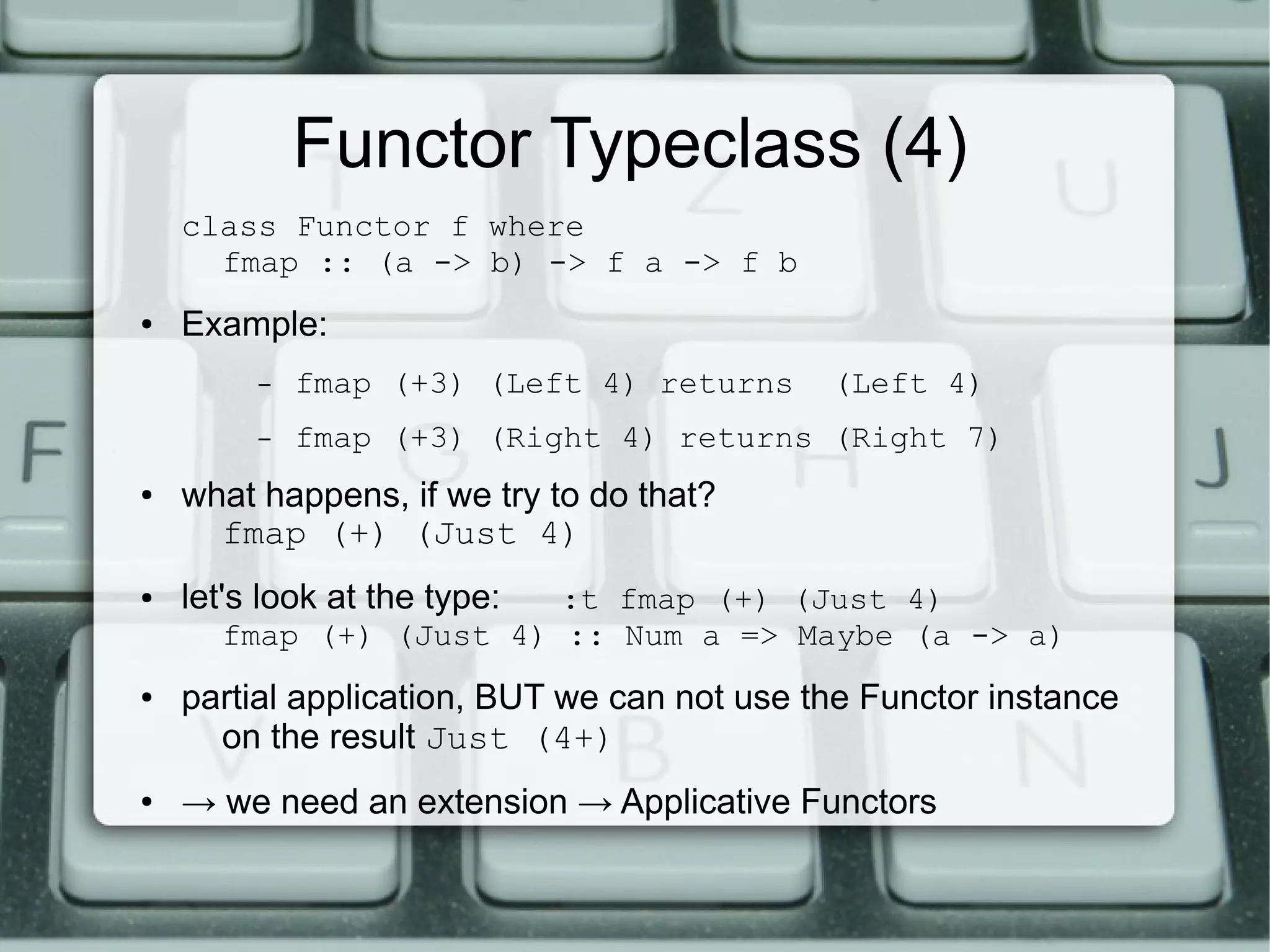
![Functor Typeclass (1)
class Functor f where
fmap :: (a -> b) -> f a -> f b
● for things that can be mapped over
● !!! Functor needs Types with kind * -> * !!!
● fmap gets a function and a type and maps the function
over the type variable → the type variable can change!
● Instance for List:
instance Functor [] where
fmap = map
– Example: fmap (*2) [2,3,4] returns [4,6,8]](https://image.slidesharecdn.com/09-haskellcontext-130228215148-phpapp01/75/09-haskell-Context-17-2048.jpg)


![Lifting a Function
● if we partial apply fmap, the header has the following structure
:t fmap (*2) results in
fmap (*2) :: (Num a, Functor f) => f a -> f a
:t fmap (cycle 3) results in
fmap (cycle 3) :: (Functor f) => f a -> f [a]
● → this is called lifting a function
● → we can predefine a normal function which gets a Functor
and returns a Functor
● → we move the function inside the Type and operate on type
variables
● → we lift the function up to the type → normal function can
work with complex types](https://image.slidesharecdn.com/09-haskellcontext-130228215148-phpapp01/75/09-haskell-Context-21-2048.jpg)


![Applicative Functor (3)
class (Functor f) => Applicative f where
pure :: a -> f a
(<*>) :: f (a -> b) -> f a -> f b
● Instance for []
instance Applicative [] where
pure x = [x]
fs <*> xs = [f x | f <- fs, x <- xs]
● Example:
– [(*0),(+100),(^2)] <*> [1,2,3]
returns [0,0,0,101,102,103,1,4,9]
– pure "Hey" :: [String] returns ["Hey"]
– [(+),(*)] <*> [1,2] <*> [3,4]
returns [4,5,5,6,3,4,6,8]](https://image.slidesharecdn.com/09-haskellcontext-130228215148-phpapp01/75/09-haskell-Context-24-2048.jpg)
![Applicative Functor (4)
● pure f <*> x equals fmap f x
● → in Control.Applicative exists a specific function
(<$>) :: (Functor f) => (a -> b) -> f a -> f b
f <$> x = fmap f x
● So we can do the same much prettier:
(++) <$> Just "johntra" <*> Just "volta"
returns Just "johntravolta"
(++) <$> ["ha","heh","hmm"] <*> ["?","!","."]
returns ["ha?", "ha!", "ha.", "heh?", "heh!",
"heh.", "hmm?", "hmm!", "hmm."]](https://image.slidesharecdn.com/09-haskellcontext-130228215148-phpapp01/75/09-haskell-Context-25-2048.jpg)


![Applicative Context
● Applicative Types can bee seen as Types with context:
– Maybe, Either for things which can fail
– [ ] as non-deterministic result
– IO as values send or get from outside
● Applicative functors allows us to operate in applicative types
like normal types and provide the context!
● → We don't need to pattern match against the Context in
every operation we use in our functions!](https://image.slidesharecdn.com/09-haskellcontext-130228215148-phpapp01/75/09-haskell-Context-28-2048.jpg)

![Sources
[1] Haskell-Tutorial: Learn you a Haskell (http://learnyouahaskell.com/,
2012/03/15)
[2] The Hugs User-Manual (
http://cvs.haskell.org/Hugs/pages/hugsman/index.html, 2012/03/15)
[3] The Haskellwiki (http://www.haskell.org/haskellwiki, 2012/03/15)](https://image.slidesharecdn.com/09-haskellcontext-130228215148-phpapp01/75/09-haskell-Context-30-2048.jpg)