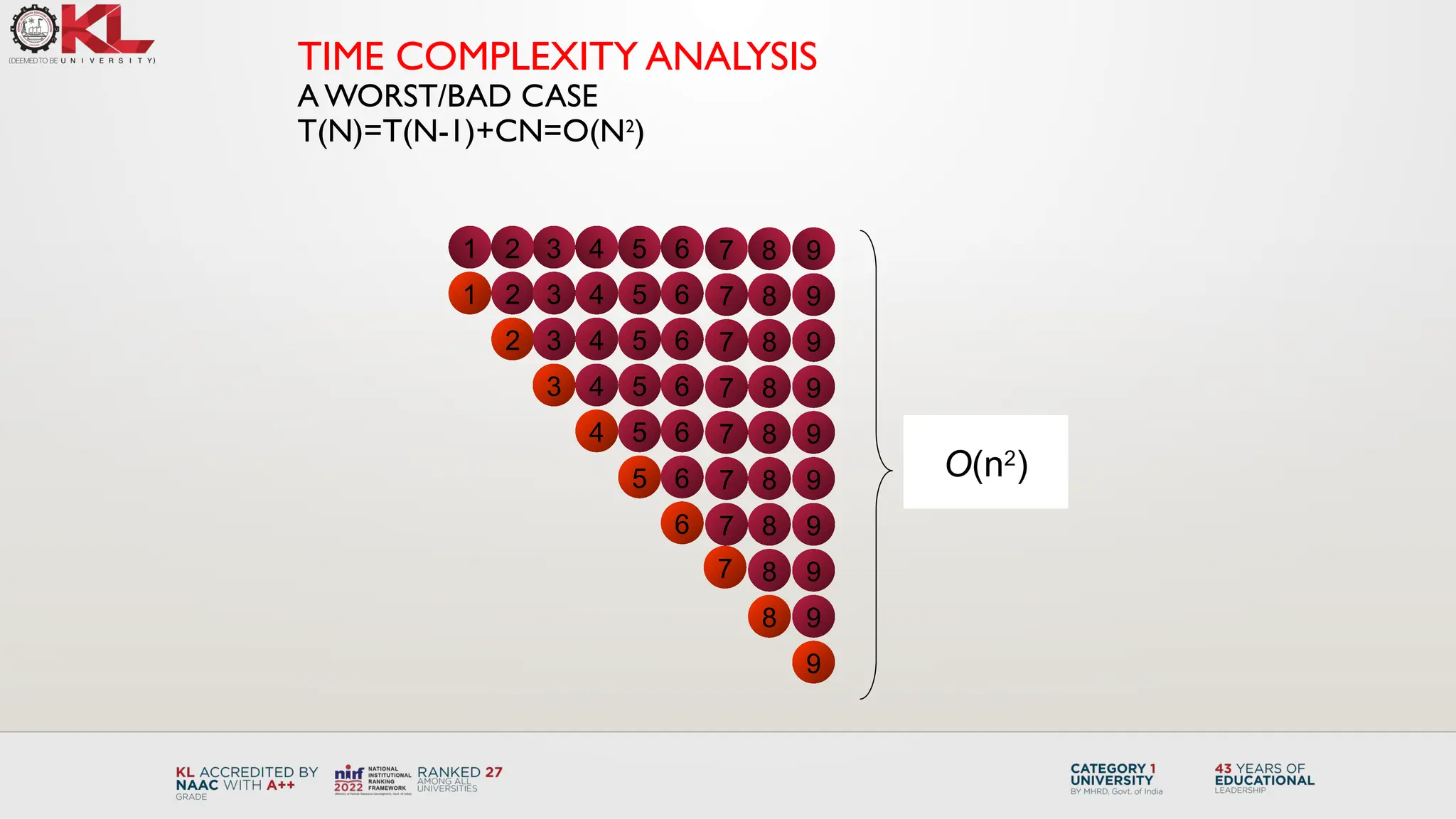
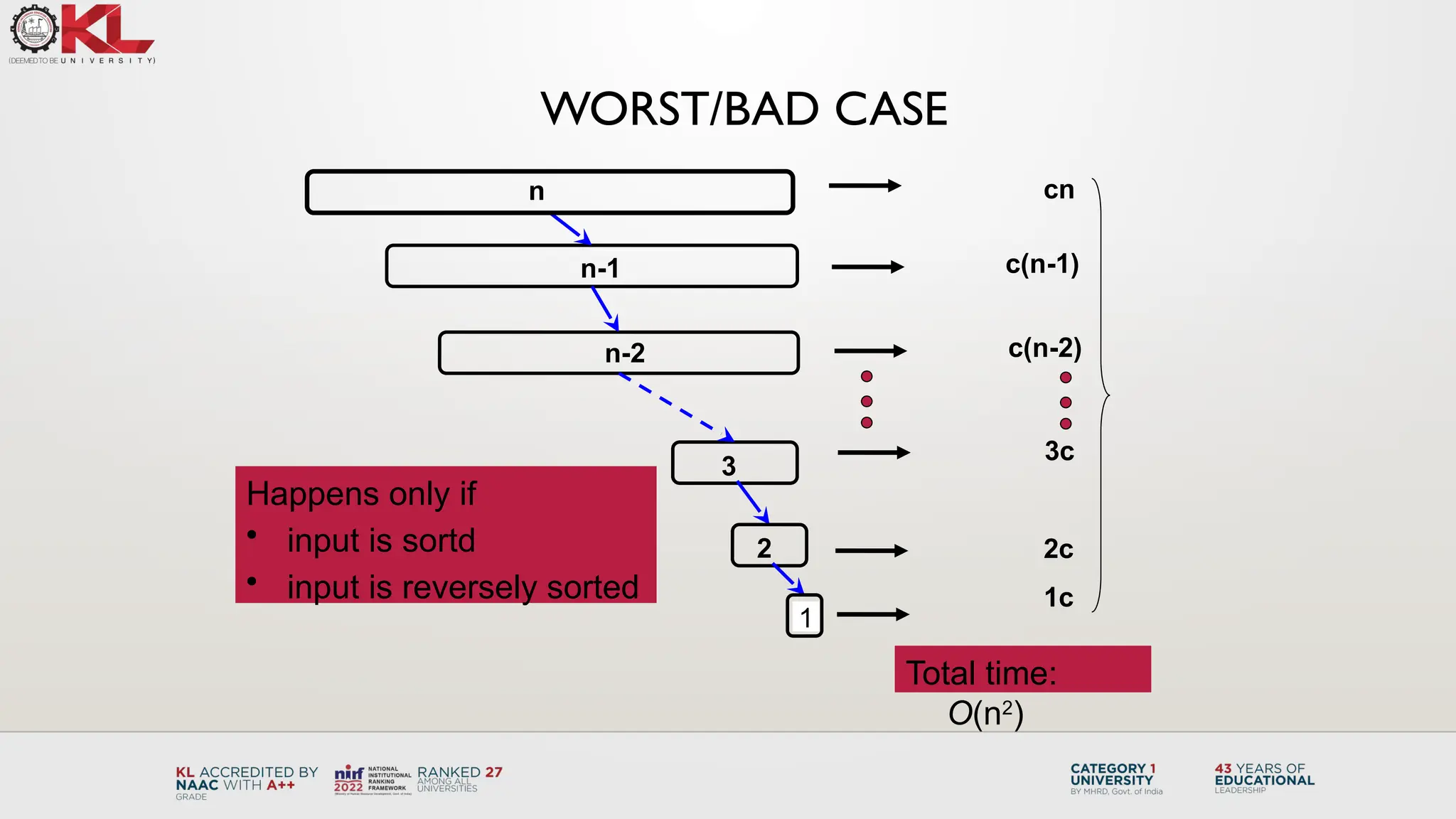
The document discusses the design and analysis of the Quick Sort algorithm, a divide and conquer method that partitions an array around a chosen pivot, leading to recursive sorting of subarrays. Different pivot selection methods are outlined, including picking the first, last, random, or median values, and time complexities for best, average, and worst cases are analyzed. Example problems and comparisons with Merge Sort are also included to enhance understanding of the algorithm's efficiency and application.


![QUICKSORT
• Sort an array A[p…r]
• Divide
– Partition the array A into 2 subarrays A[p..q] and A[q+1..r], such that
each element of A[p..q] is smaller than or equal to each element in
A[q+1..r]
– Need to find index q to partition the array
≤
A[p…q] A[q+1…r]](https://image.slidesharecdn.com/09quicksort-241213112654-2b72718e/75/09-QUICK-SORT-Design-and-Analysis-of-algorithms-3-2048.jpg)
![QUICKSORT
• Conquer
– Recursively sort A[p..q] and A[q+1..r] using Quicksort
• Combine
– Trivial: the arrays are sorted in place
– No additional work is required to combine them
– The entire array is now sorted
A[p…q]
A[q+1…r]
≤](https://image.slidesharecdn.com/09quicksort-241213112654-2b72718e/75/09-QUICK-SORT-Design-and-Analysis-of-algorithms-4-2048.jpg)

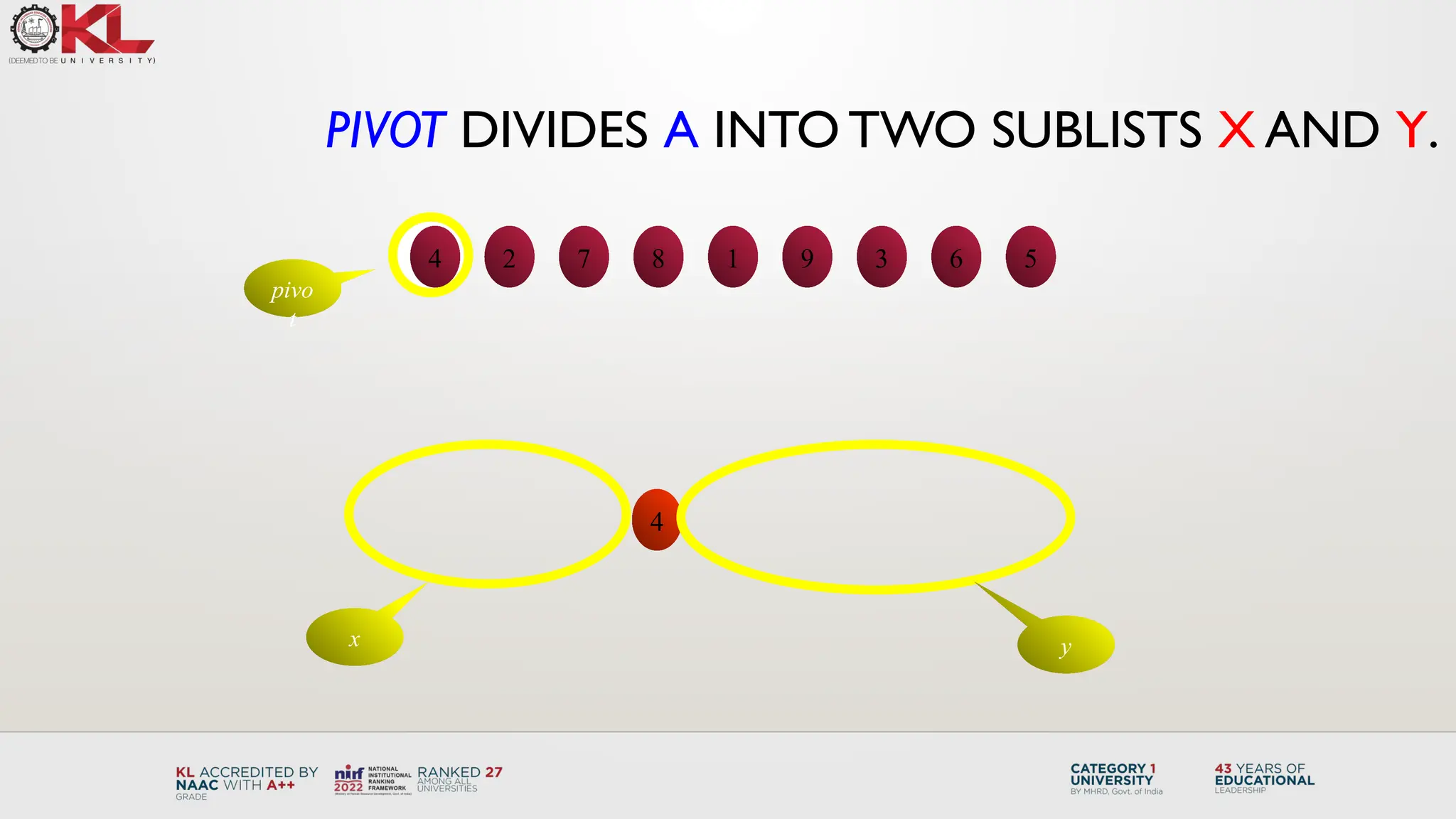
![Keep going from left side as long as a[ i ]<pivot and from the right
side as long as a[ j ]>pivot
85 24 63 95 17 31 45 98
i j
85 24 63 95 17 31 45 98
85 24 63 95 17 31 45 98
85 24 63 95 17 31 45 98
i
i
i
j
j
j
Example :
Process:
pivot](https://image.slidesharecdn.com/09quicksort-241213112654-2b72718e/75/09-QUICK-SORT-Design-and-Analysis-of-algorithms-7-2048.jpg)



![Quick Sort Algorithm :
Algorithm QuickSort(low,high)
//Sorts the elements a[low],…..,a[high] which resides in the global array a[1:n] into //ascending
order;
// a[n+1] is considered to be defined and must ≥ all the elements in a[1:n].
{
if( low< high ) // if there are more than one element
{ // divide p into two subproblems.
j :=Partition(low,high);
// j is the position of the partitioning element.
QuickSort(low,j-1);
QuickSort(j+1,high);
//There is no need for combining solutions.
}
}](https://image.slidesharecdn.com/09quicksort-241213112654-2b72718e/75/09-QUICK-SORT-Design-and-Analysis-of-algorithms-11-2048.jpg)
![Algorithm Partition(l,h)
{
pivot:= a[l] ; i:=l; j:= h+1;
while( i < j ) do
{
i++;
while( a[ i ] < pivot ) do
i++;
j--;
while( a[ j ] > pivot ) do
j--;
if ( i < j ) then Interchange(i,j ); // interchange ith
and
} // jth
elements.
Interchange(l, j ); return j; // interchange pivot and jth
element.
}](https://image.slidesharecdn.com/09quicksort-241213112654-2b72718e/75/09-QUICK-SORT-Design-and-Analysis-of-algorithms-12-2048.jpg)
![Algorithm interchange (x,y )
{
temp=a[x];
a[x]=a[y];
a[y]=temp;
}](https://image.slidesharecdn.com/09quicksort-241213112654-2b72718e/75/09-QUICK-SORT-Design-and-Analysis-of-algorithms-13-2048.jpg)