815.07 machine learning using python.pdf

Recursion and
Dynamic Programming
Biostatistics 615/815
Lecture 7

Notes on Problem Set 1
z Results were very positive!
• But homework was time-consuming…
z Familiar with
• Union Find algorithms
• Compiling and Executing C Programs

Question 1
z How many random pairs of connections
are required to connect 1,000 objects?
• Answer: ~3,740
z Useful notes:
• Number of non-redundant links to controls loop
• Repeat simulation to get a better estimates

Question 2
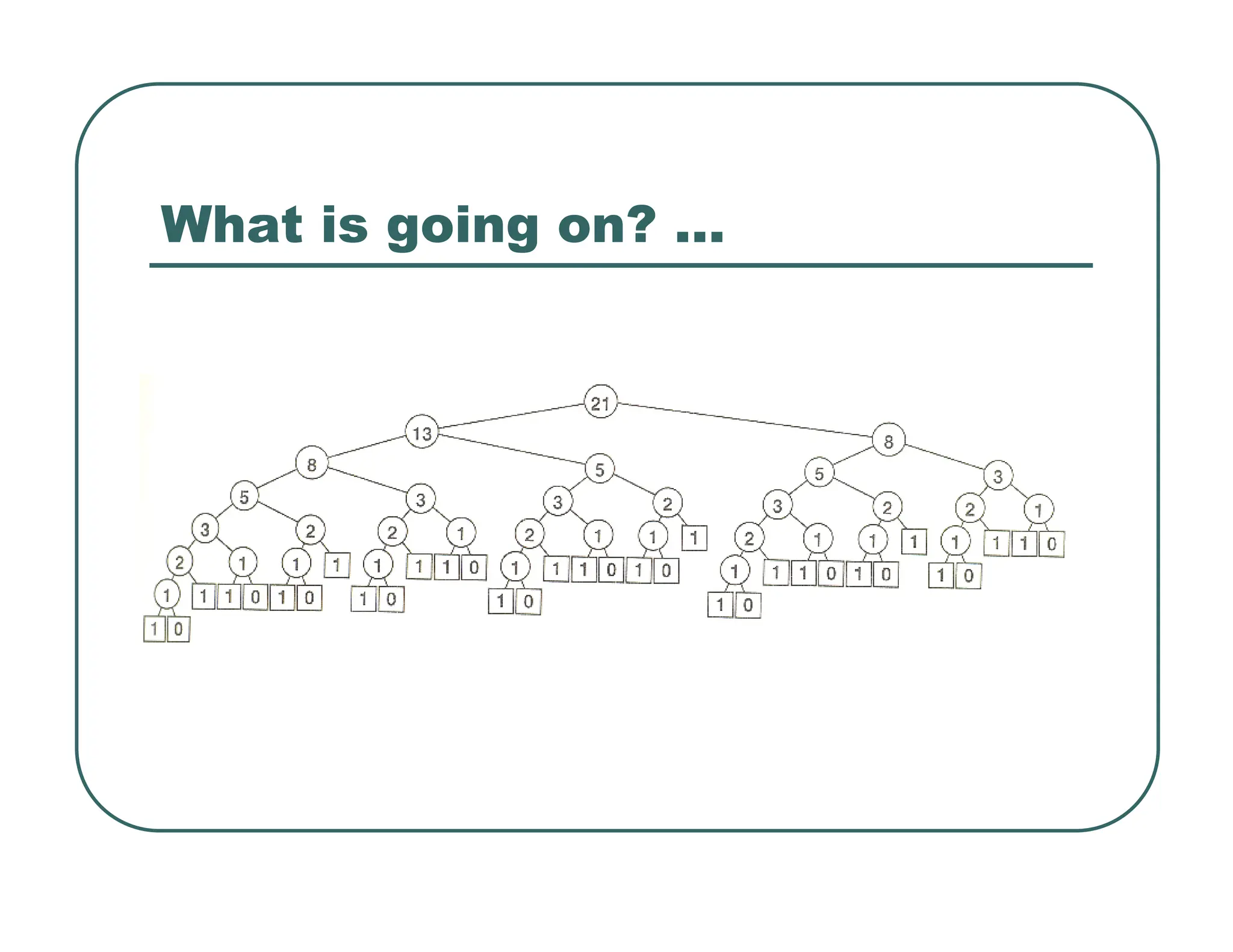
z Path lengths in the saturated tree…
• ~1.8 nodes on average
• ~5 nodes for maximum path
z Random data is far from worst case
• Worst case would be paths of log2 N nodes
z Path lengths can be calculated using weights[]

Question 3
z Tree height or weight for optimal quick union
operations?
• Using height ensures that longest path is shorter.
• Pointing the root of a tree with X nodes to the root of a
tree with Y nodes, increases the average length of all
paths by X/N.
• Smallest average length and faster Find operations
correspond to choosing X < Y.
• Easiest to check if you use the same sequence of
random numbers for both problems.

Last Lecture
z Principles for analysis of algorithms
• Empirical Analysis
• Theoretical Analysis
z Common relationships between inputs
and running time
z Described two simple search algorithms

Recursive refers to …
z A function that is part of its own definition
e.g.
z A program that calls itself
⎪
⎩
⎪
⎨
⎧
=
>
−
⋅
=
0
N
if
1
0
N
if
)
1
(
)
(
N
Factorial
N
N
Factorial

Key Applications of Recursion
z Dynamic Programming
• Related to Markov processes in Statistics
z Divide-and-Conquer Algorithms
z Tree Processing

Recursive Function in R
Factorial <- function(N)
{
if (N == 0)
return(1)
else
return(N * Factorial(N - 1))
}

Recursive Function in C
int factorial (int N)
{
if (N == 0)
return 1;
else
return N * factorial(N - 1);
}

Key Features of Recursions
z Simple solution for a few cases
z Recursive definition for other values
• Computation of large N depends on smaller N
z Can be naturally expressed in a function
that calls itself
• Loops are sometimes an alternative

A Typical Recursion:
Euclid’s Algorithm
z Algorithm for finding greatest common
divisor of two integers a and b
• If a divides b
• GCD(a,b) is a
• Otherwise, find the largest integer t such that
• at + r = b
• GCD(a,b) = GCD(r,a)

Euclid’s Algorithm in R
GCD <- function(a, b)
{
if (a == 0)
return(b)
return(GCD(b %% a, a))
}

Euclid’s Algorithm in C
int gcd (int a, int b)
{
if (a == 0)
return b;
return gcd(b % a, a);
}

Evaluating GCD(4458, 2099)
gcd(2099, 4458)
gcd(350, 2099)
gcd(349, 350)
gcd(1, 349)
gcd(0, 1)

Divide-And-Conquer Algorithms
z Common class of recursive functions
z Common feature
• Process input
• Divide input in smaller portions
• Recursive call(s) process at least one portion
z Recursion may sometimes occur before input
is processed

Recursive Binary Search
int search(int a[], int value, int start, int stop)
{
// Search failed
if (start > stop)
return -1;
// Find midpoint
int mid = (start + stop) / 2;
// Compare midpoint to value
if (value == a[mid]) return mid;
// Reduce input in half!!!
if (value < a[mid])
return search(a, start, mid – 1 };
else
return search(a, mid + 1, stop);
}

Recursive Maximum
int Maximum(int a[], int start, int stop)
{
int left, right;
// Maximum of one element
if (start == stop)
return a[start];
left = Maximum(a, start, (start + stop) / 2);
right = Maximum(a, (start + stop) / 2 + 1, stop);
// Reduce input in half!!!
if (left > right)
return left;
else
return right;
}

An inefficient recursion
z Consider the Fibonacci numbers…
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
−
+
−
=
=
=
)
2
(
)
1
(
1
N
if
1
0
N
if
0
)
(
N
Fibonacci
N
Fibonacci
N
Fibonacci

Fibonacci Numbers
int Fibonacci(int i)
{
// Simple cases first
if (i == 0)
return 0;
if (i == 1)
return 1;
return Fibonacci(i – 1) + Fibonacci(i – 2);
}

Terribly Slow!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
Time
0
10
20
30
40
50
60
Fibonacci Number
Time (seconds)
Calculating Fibonacci Numbers Recursively

Faster Alternatives
z Certain quantities are recalculated
• Far too many times!
z Need to avoid recalculation…
• Ideally, calculate each unique quantity once.

Dynamic Programming
z A technique for avoiding recomputation
z Can make exponential running times …
z … become linear!

Bottom-Up Dynamic Programming
z Evaluate function starting with smallest possible
argument value
• Stepping through possible values, gradually increase
argument value
z Store all computed values in an array
z As larger arguments evaluated, precomputed
values for smaller arguments can be retrieved

Fibonacci Numbers in C
{
int fib[LARGE_NUMBER], j;
fib[0] = 0;
fib[1] = 1;
for (j = 2; j <= i; j++)
fib[j] = fib[j – 1] + fib[j – 2];
return fib[i];
}

Fibonacci With Dynamic Memory
{
int * fib, j, result;
if (i < 2) return i;
fib = malloc(sizeof(int) * (i + 1));
fib[0] = 0; fib[1] = 1;
for (j = 2; j <= i; j++)
fib[j] = fib[j – 1] + fib[j – 2];
result = fib[i];
free(fib);
return result;
}

Fibonacci Numbers in R
Fibonacci <- function(i)
{
if (i < 2)
return(i)
// Arrays in R are zero based, so ensure i >= 1
i <- i + 1
fib <- rep(0, i)
fib[1] <- 0;
fib[2] <- 1;
for (j in seq(3,i))
fib[j] <- fib[j – 1] + fib[j – 2]
return (fib[i])
}

Top-Down Dynamic Programming
z Save each computed value as final
action of recursive function
z Check if pre-computed value exists as
the first action

Fibonacci Numbers
{
// Simple cases first
if (saveF[i] > 0)
return saveF[i];
if (i <= 1)
return i;
// Recursion
saveF[i] = Fibonacci(i – 1) + Fibonacci(i – 2);
return saveF[i];
}

Implementing Function in R
z Within R functions, all assignments
change only local variable by default
z Must use <<- operator to change global
variable

Fibonacci Numbers
Fibonacci <- function(i)
{
# Simple cases first
if (i <= 1)
return (i)
if (saveF[i] > 0)
return (saveF[i])
# Recursion
saveF[i] <<- Fibonacci(i – 1) + Fibonacci(i – 2)
return (saveF[i])
}

Dynamic Programming
Top-down vs. Bottom-up
z In bottom-up programming, programmer
has to do the thinking by selecting values
to calculate and order of calculation
z In top-down programming, recursive
structure of original code is preserved, but
unnecessary recalculation is avoided.

Examples of Useful Settings for
Dynamic Programming
z Calculating Binomial Coefficients
z Evaluating Poisson-Binomial Distribution

Binomial Coefficients
z The number of subsets with k elements
from a set of size N
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛ −
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
1
1
1
k
N
k
N
k
N
1
0
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
N
N
N

Implementation in R
Choose <- function(N, k)
{
M <- matrix(nrow = N, ncol = N + 1)
for (i in 1:N)
{
M[i,1] <- M[i, i + 1] <- 1
if (i > 1)
for (j in 2:i)
M[i,j] <- M[i - 1, j - 1] + M[i - 1, j];
}
return(M[N,k + 1])
}

Implementation in C
int Choose(int N, int k)
{
int i, j, M[MAX_N][MAX_N];
for (i = 1; i <= N; i++)
{
M[i][0] = M[i][i] = 1;
for (j = 1; j < i; j++)
M[i][j] = M[i - 1][j - 1] + M[i - 1][j];
}
return M[N][k];
}

Poisson-Binomial Distribution
z X1, X2, …, Xn are Bernoulli random
variables
z Probability of success is pk for Xk
z ∑kXk has Poisson-Binomial Distribution

Recursive Formulation
)
1
(
)
1
(
)
1
(
)
(
)
1
(
)
(
)
0
(
)
1
(
)
0
(
)
1
(
1
)
0
(
1
1
1
1
1
1
1
1
−
−
+
−
=
−
=
−
=
=
−
=
−
−
−
−
j
P
p
i
P
p
i
P
j
P
p
j
P
P
p
P
p
P
p
P
j
j
j
j
j
j
j
j
j
j
j

Summary
z Recursive functions
z The stack
z Dynamic programming
• Bottom-up Dynamic Programming
• Top-down Dynamic Programming

Reading
z Sedgewick, Chapters 5.1 – 5.3
z Notice:
• No class on Monday, October 4
• Public Health Symposium on
“Global Health – The Challenge of Inequality”
At Rackham Auditorium

815.07 machine learning using python.pdf

More Related Content

Similar to 815.07 machine learning using python.pdf

Recently uploaded

815.07 machine learning using python.pdf