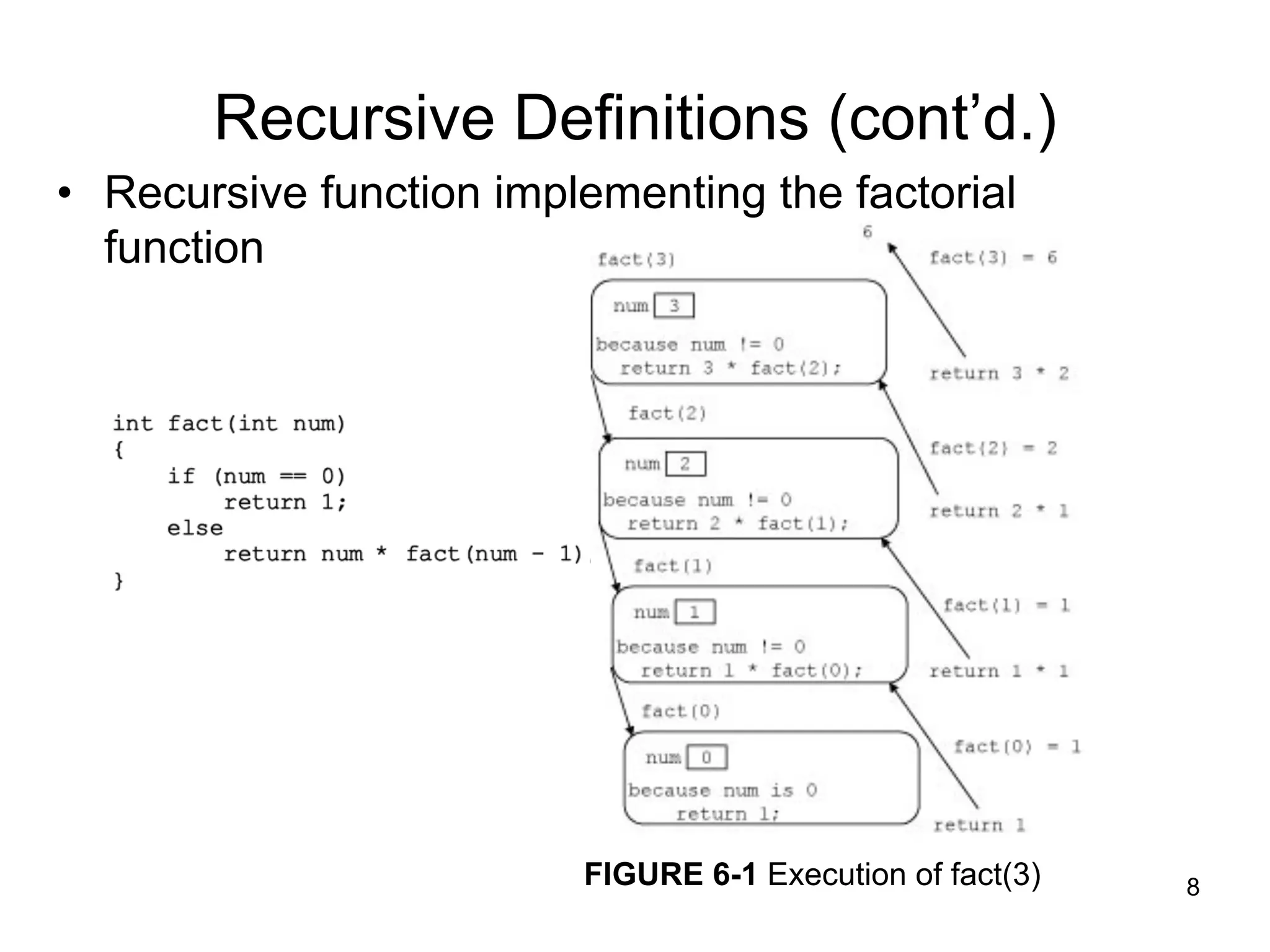
1) Recursion is a technique where a function calls itself to solve a problem. It breaks the problem down into smaller subproblems until it reaches a base case that can be solved directly.
2) A recursive function must have a base case where it does not call itself further, and a general case where it calls itself on a reduced problem. It works by repeatedly reducing the problem size until the base case is reached.
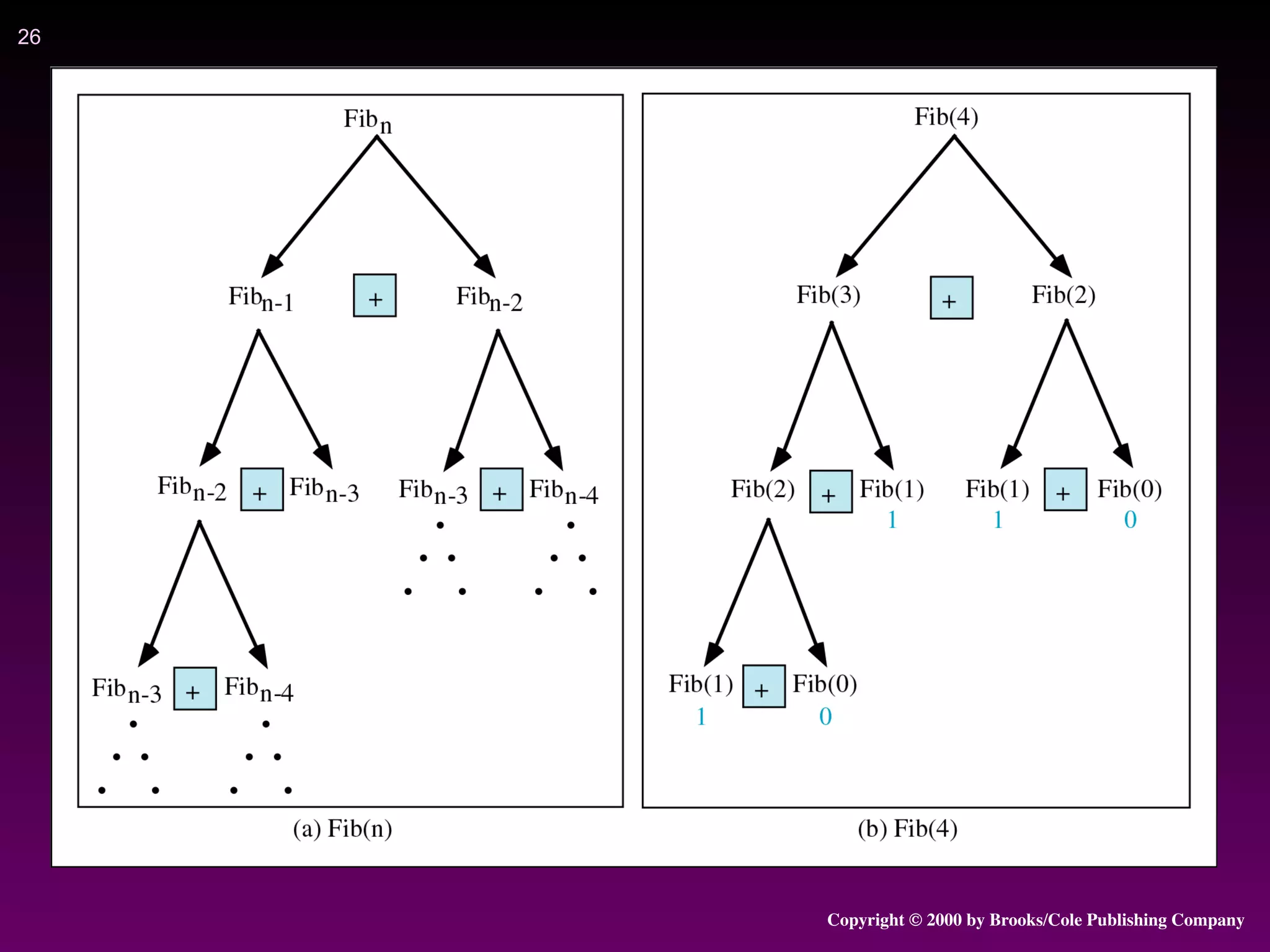
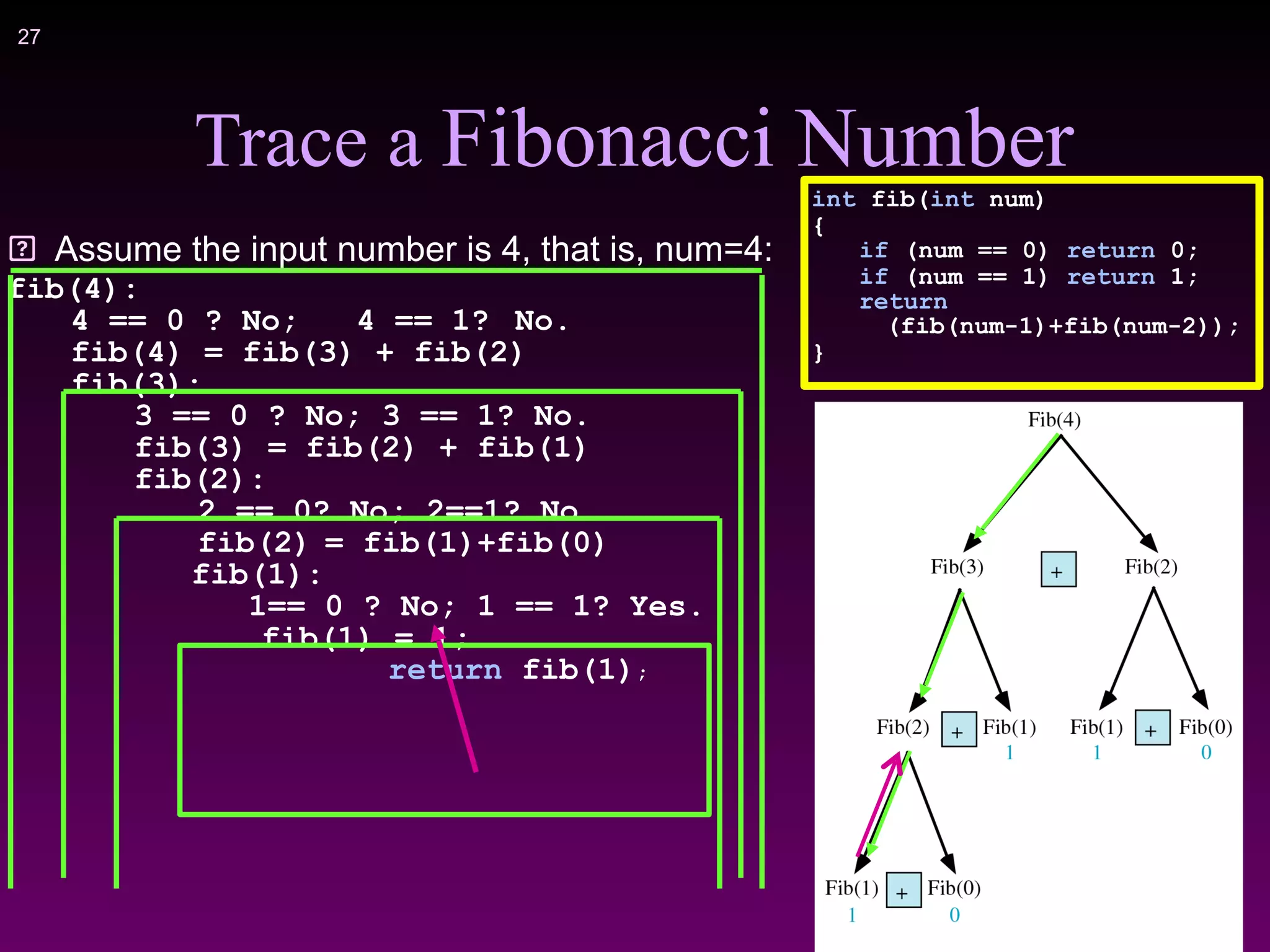
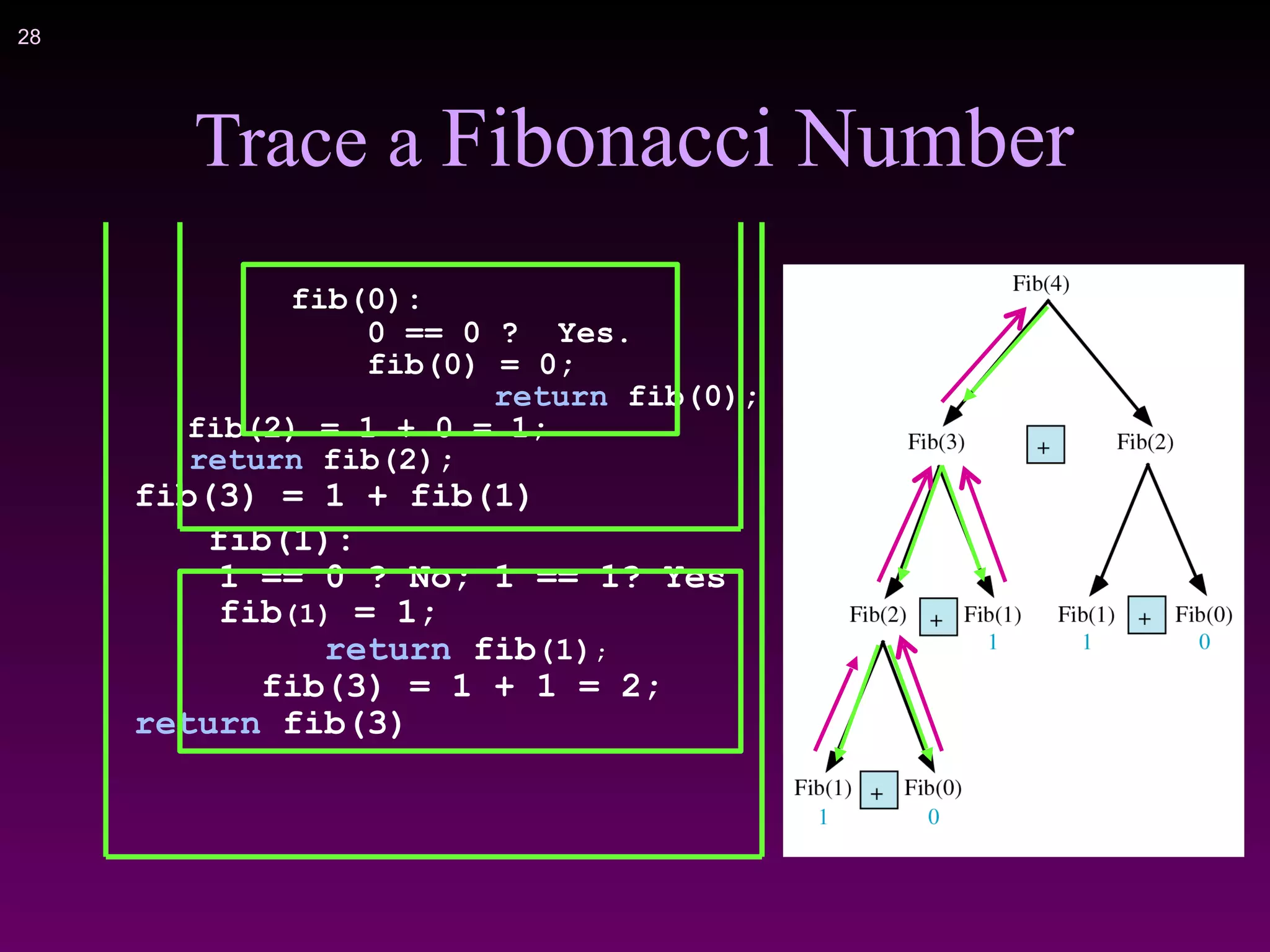
3) Examples of problems that can be solved recursively include calculating factorials, Fibonacci numbers, binary search of a sorted array, checking if a string is a palindrome, and solving the Towers of Hanoi puzzle.
























![!30
Example 4: Fibonacci number w/o
recursion
//Calculate Fibonacci numbers iteratively
//much more efficient than recursive solution
int fib(int n)
{
int f[100];
f[0] = 0; f[1] = 1;
for (int i=2; i<= n; i++)
f[i] = f[i-1] + f[i-2];
return f[n];
}](https://image.slidesharecdn.com/recursion-230712151032-58b115b8/75/Recursion-pdf-30-2048.jpg)


![!33
Binary Search with Recursion
// Searches an ordered array of integers using recursion
int bsearchr(const int data[], // input: array
int first, // input: lower bound
int last, // input: upper bound
int value // input: value to find
)// output: index if found, otherwise return –1
{ //cout << "bsearch(data, "<<first<< ", last "<< ", "<<value << "); "<<endl;
int middle = (first + last) / 2;
if (data[middle] == value)
return middle;
else if (first >= last)
return -1;
else if (value < data[middle])
return bsearchr(data, first, middle-1, value);
else
return bsearchr(data, middle+1, last, value);
}](https://image.slidesharecdn.com/recursion-230712151032-58b115b8/75/Recursion-pdf-33-2048.jpg)
![!34
Binary Search
int main() {
const int array_size = 8;
int list[array_size]={1, 2, 3, 5, 7, 10, 14, 17};
int search_value;
cout << "Enter search value: ";
cin >> search_value;
cout << bsearchr(list,0,array_size-1,search_value)
<< endl;
return 0;
}](https://image.slidesharecdn.com/recursion-230712151032-58b115b8/75/Recursion-pdf-34-2048.jpg)
![!35
Binary Search w/o recursion
// Searches an ordered array of integers
int bsearch(const int data[], // input: array
int size, // input: array size
int value // input: value to find
){ // output: if found,return
// index; otherwise, return -1
int first, last, upper;
first = 0;
last = size - 1;
while (true) {
middle = (first + last) / 2;
if (data[middle] == value)
return middle;
else if (first >= last)
return -1;
else if (value < data[middle])
last = middle - 1;
else
first = middle + 1;
}
}](https://image.slidesharecdn.com/recursion-230712151032-58b115b8/75/Recursion-pdf-35-2048.jpg)




![!40
Think Recursively
Many of the problems can be solved easily using recursion if you
think recursively. For example, the palindrome problem can be
solved recursively as follows:
bool isPalindrome(const char * const s)
{
if (strlen(s) <= 1) // Base case
return true;
else if (s[0] != s[strlen(s) - 1]) // Base case
return false;
else
return isPalindrome(substring(s, 1, strlen(s) - 2));
}](https://image.slidesharecdn.com/recursion-230712151032-58b115b8/75/Recursion-pdf-40-2048.jpg)
![!41
Recursive Helper Methods
The preceding recursive isPalindrome method is not efficient, because it creates a
new string for every recursive call. To avoid creating new strings, use a helper
method:
bool isPalindrome(const char * const s, int low, int high)
{
if (high <= low) // Base case
return true;
else if (s[low] != s[high]) // Base case
return false;
else
return isPalindrome(s, low + 1, high - 1);
}
bool isPalindrome(const char * const s)
{
return isPalindrome(s, 0, strlen(s) - 1);
}](https://image.slidesharecdn.com/recursion-230712151032-58b115b8/75/Recursion-pdf-41-2048.jpg)



![!45
Eight Queens
0
4
7
5
2
6
1
3
queens[0]
queens[1]
queens[2]
queens[3]
queens[4]
queens[5]
queens[6]
queens[7]
Place eight queens on the chessboard such that no queen attacks
any other one.](https://image.slidesharecdn.com/recursion-230712151032-58b115b8/75/Recursion-pdf-45-2048.jpg)
![!46
bool empty(int t[], int row, int col) {
for( int j = 0; j < row; j++) {
if (t[j] == col) //same column
return false;
if (abs(t[j] - col) == (row - j)) //on cross line
return false;
}
return true;
}
bool queens(int t[], int row, int col) {
if (row == SIZE) // found one answer
return true;
for (col = 0; col <SIZE; col++)
{
t[row] = col;
if (empty(t, row, col) && queens(t, row +1, 0))
return true;
}
return false;
}](https://image.slidesharecdn.com/recursion-230712151032-58b115b8/75/Recursion-pdf-46-2048.jpg)
![void print(int t[]){
// print solution
for(int i = 0; i < SIZE; i++) {
for(int j = 0; j < SIZE; j++) {
if (j == t[i])
cout << " Q ";
else
cout << " _ ";
}
cout << endl;
}
}
int main() {
int t[SIZE]={0};
for (int i= 0; i <SIZE; i++){
t[0] = i; //on first row, Queen on different column
cout << endl << endl <<"i is: " << i << endl;
if (queens(t, 1,0))
print(t);
}
}](https://image.slidesharecdn.com/recursion-230712151032-58b115b8/75/Recursion-pdf-47-2048.jpg)