06 Recursion in C.pptx

Programming and Data Structures

*What is Recursion?
*Some Examples
*Recursion - Mechanism of Execution
*Recursion versus Iteration
*Function Call Implementation
Today’s Discussion…
3

Recursion
5
•A process by which a function calls itself repeatedly.
• Such a function is called a recursive function
• Recursion may be direct or cyclically in a chain
•Direct recursion.
•When a function f(…) calls f(…).
•Cyclically in a chain recursion.
•f1(…) calls f2(…) , f2(…) calls f3(…) . . . fi(…)
calls f1(…)

Some Examples of Recursion
6
•Example 1: GCD of two positive integers
gcd(10, 15) = 5, gcd(11, 13) = 1
gcd(m,n) = gcd(m-n,n), if m>n else gcd(m,n-m)
• Example 2: Recursion formula
T(n) = n + 2×T(n-1)
T(100) = ?
• Example 2: Tower of Hanoi
Move n disks from A C
= move (n-1) disks from A to B
+ move the disk from A to C
+ move (n-1) disk from B to C

Some Examples of Recursion
7
•Example 1: Factorial calculation
n! = n× (n-1)×(n-2) ×…×3×2×1
n! = n×(n-1)!
factorial(n) = n×factorial(n-1)
• Example 2: Fibonacci number sequence
1, 1, 2, 3, 5, 8, 13, 21, …..
ni = ni-1 + ni-2
fibonacci(n) = fibonacci(n-1) + fibonacci(n-2)

Important Points to be Noted
8
•For a function to be written in recursive form, two conditions are to
be satisfied:
•Condition 1
• It should be possible to express the problem in recursive form.
•Condition 2
• The problem statement must include a stopping condition.

9
•It should be possible to express the problem in recursive form.
Examples
gcd(m,n) = if m>n gcd(m-n, n) else gcd(m, n-m)
T(n) = n + 2×T(n-1)

10
•The problem statement must include a stopping condition.
Examples
• factorial(0) = 1
• fibonacci(0) = 0; fibonacci(1) = 1
gcd(m,n) = if m>n gcd(m-n,n) else gcd(m,n-m)
• gcd(m, m) = m
T(n) = n + 2×T(n-1)
• T(0) = 0

Recursive Function for n!
12
#include <stdio.h>
int fact(int n)
{
if (n == 0)
return 1;
else
return (n * fact(n-1));
}
void main()
{
int x;
scanf(“%d”, &x);
printf (“Factorial of %d is: %d”, x, fact(x));
}
fact(0) = 1
fact(n) = n × fact(n-1), if n > 0

Factorial Execution
13
When a recursive program is executed, the recursive function
calls are not executed immediately.
* They are kept aside (on a stack) until the stopping condition is
encountered.
* The function calls are then executed in reverse order.

Factorial Execution
14
if (1 = = 0) return (1);
else return (1 * fact(0));
fact(4)
if (4 = = 0) return (1);
if (3 = = 0) return (1);
if (2 = = 0) return (1);
else return (2 * fact(1)); 1
2
6
24
int fact (int n)
{
if (n = = 0) return (1);
else return (n * fact(n-1));
}

Factorial Execution
15
• First, the function calls will be processed
fact(4) = 4 * fact(3)
fact(3) = 3 * fact(2)
fact(2) = 2 * fact(1)
fact(1) = 1 * fact(0)
• The actual values return in the reverse order
fact(0) = 1
fact(1) = 1 * 1 = 1
fact(2) = 2 * 1 = 2
fact(3) = 3 * 2 = 6
fact(4) = 4 * 6 = 24

Recursive Function for F(n)
16
#include <stdio.h>
int fibo(int n)
{
if (n < 2)
return n;
else
return (fibo(n-1) + fibo(n-2));
}
void main()
{
int x;
printf (“%d-th Fibonacci number is %d n”, x, fibo(x));
}
fibo(0) = 0; fibo(1) = 1
fibo(n) = fibo(n-1) + fibo(n-2), if n > 2

Fibonacci Series Execution
17
f(0) = 0
f(1) = 1
f(n) = f(n-1)+f(n-2),if n>1
f(4)
f(3) f(2)
f(1)
f(2) f(0)
f(1)
f(1) f(0)
int f(int n)
{
if (n < 2)
return (n);
else
return (f(n-1) + f(n-2));
}

Tracing Execution
18
f(4)
f(3) f(2)
f(1)
f(2) f(0)
f(1)
f(1) f(0)
*How many times is the function
called when evaluating f(4) ?
*Inefficiency:
*Same thing is computed several
times. called 9 times

Recursive Function for gcd(m,n)
19
#include <stdio.h>
int gcd(int m, int n)
{
if (m == n)
return m;
else
if (m > n) return (gcd(m-n, n);
else return gcd(m, n-m);
}
void main()
{
int x, y;
scanf(“x = %d, y = %d”, &x, &y);
printf (“GCD of %d and %d is %d”, x, y, gcd(x, y));
}
gcd(m,m) = m;
gcd(m,n) = gcd(m-n, n) if m > n
= gcd(m, n-m) else

GCD Execution
20
g(10,15)
{
if (m == n)
return m;
else
if(m > n) return (gcd(m-n,n);
}
gcd(m,m) = m;
gcd(m,n) = gcd(m-n, n) if m > n
= gcd(m, n-m) else
g(10, 5)
g(5,5)

Performance Comparison of GCDs
21
{
if (m == n)
return m;
else
if(m > n) return (gcd(m-n,n);
}
gcd(m,n) = m, if m = n
= gcd(m-n,n) if m>n
= gcd(m,n-m) else
gcd(m,n) = m, if (m = n) or n = 0;
= gcd(n,m) if n>m
= gcd(m%n,m)
{
if ((m == n)|| (n == 0))
return m;
else
if(n > m) return (gcd(n,m);
else return gcd(m, n%m);
}
Compare the performance of the above-mentioned two versions of gcd calculations

Recursive Function for T(n)
22
#include <stdio.h>
int T(int n)
{
if (n == 0)
return 0;
else
return (n + 2*T(n-1));
}
void main()
{
int x;
printf (“T(%d”)= %d”, x, T(x));
}
T(0) = 0
T(n) = n + 2 × T(n-1), if n > 0

Towers of Hanoi Problem
23
5
4
3
2
1
A B C

24
• The problem statement
• Initially all the disks are stacked on the A pole.
• Required to transfer all the disks to the C pole.
1.Only one disk may be moved at a time.
2.Each move consists of taking the upper disk from one of the stacks and placing it on top of
another stack or on an empty rod.
3.No disk may be placed on top of a disk that is smaller than it.
* With 3 disks, the puzzle can be solved in 7 moves. The minimal number of moves required
to solve a Tower of Hanoi puzzle is 2n − 1, where n is the number of disks.
• C pole is used for temporary storage of disks.

25
• Recursive statement of the general problem of n disks
• Step 1:
• Move the top (n-1) disks from A to B
• Step 2:
• Move the largest disk from A to C.
• Step 3:
• Move the (n-1) disks from B to C.

26
#include <stdio.h>
void move(int n, char A, char B, char C);
int main()
{
int n; /* Number of disks */
scanf (“%d”, &n);
move (n, ‘A’, ‘B’, ‘C’);
return 0;
}
void move (int n, char A, char B, char C)
{
if (n > 0) {
move (n-1, A, C, B);
printf (“Move disk %d from %c to %c n”, n, A, C);
move (n-1, B, C, A);
}
return;
}

Towers of Hanoi – Execution
27
3
Move disk 1 from A to C
Move disk 2 from A to B
Move disk 1 from C to B
Move disk 1 from B to A
Move disk 2 from B to C
4
Move disk 1 from B to R
Move disk 1 from C to L
Move disk 1 from C to A
5
How many moves are
required for n disks?

Points to be Noted
28
1. Every recursive program can also be written without recursion.
2. Recursion is used for programming convenience, not for
performance enhancement.
3. Sometimes, if the function being computed has a nice
recurrence form, then a recursive code may be more readable.
Performance warning!
Speed: Avoid Fibonacci-style recursive programs, which result in an
exponential “explosion” of calls.
Memory: Recursive calls take consume additional memory.

Recursion Versus Iteration
29
• Repetition
• Iteration: explicit loop
• Recursion: repeated function calls
• Termination
• Iteration: Loop condition fails
• Recursion: Base case recognized
• Both can have infinite loops
• Be careful about the termination condition
• Balance
• Choice between performance (iteration) and good software engineering
(recursion).

How are function calls implemented?
30
• The following applies in general, with minor variations that are implementation
dependent.
• The system maintains a stack in memory.
• Stack is a last-in first-out structure.
• Two operations on stack, push and pop.
• Whenever there is a function call, the activation record gets pushed into the
stack.
• Activation record consists of the return address in the calling program, the return
value from the function, and the local variables inside the function.

Function calls implementation
31
main()
{
……..
x = gcd (a, b);
……..
}
int gcd (int x, int y)
{
……..
……..
return (result);
}
Return Addr
Return Value
Local
Variables
Before call After call After return
STACK
Activation
record

32
main()
{
……..
x = ncr (a, b);
……..
}
int ncr (int n, int r)
{
return (fact(n)/
fact(r)/fact(n-r));
}
LV1, RV1, RA1
Before call Call fact ncr returns
int fact (int n)
{
………
return (result);
}
3 times
LV1, RV1, RA1
fact returns
LV1, RV1, RA1
LV2, RV2, RA2
Call ncr
3 times

What happens for recursive calls?
33
• What we have seen ….
• Activation record gets pushed into the stack when a function call is made.
• Activation record is popped off the stack when the function returns.
• In recursion, a function calls itself.
• Several function calls going on, with none of the function calls returning
back.
• Activation records are pushed onto the stack continuously.
• Large stack space required.
• Activation records keep popping off, when the termination condition of
recursion is reached.

Example:: main() calls fact(3)
34
int fact (n)
int n;
{
if (n = = 0)
return (1);
else
return(n * fact(n-1));
}
main()
{
int n;
n = 3;
printf (“%d n”, fact(n) );
}

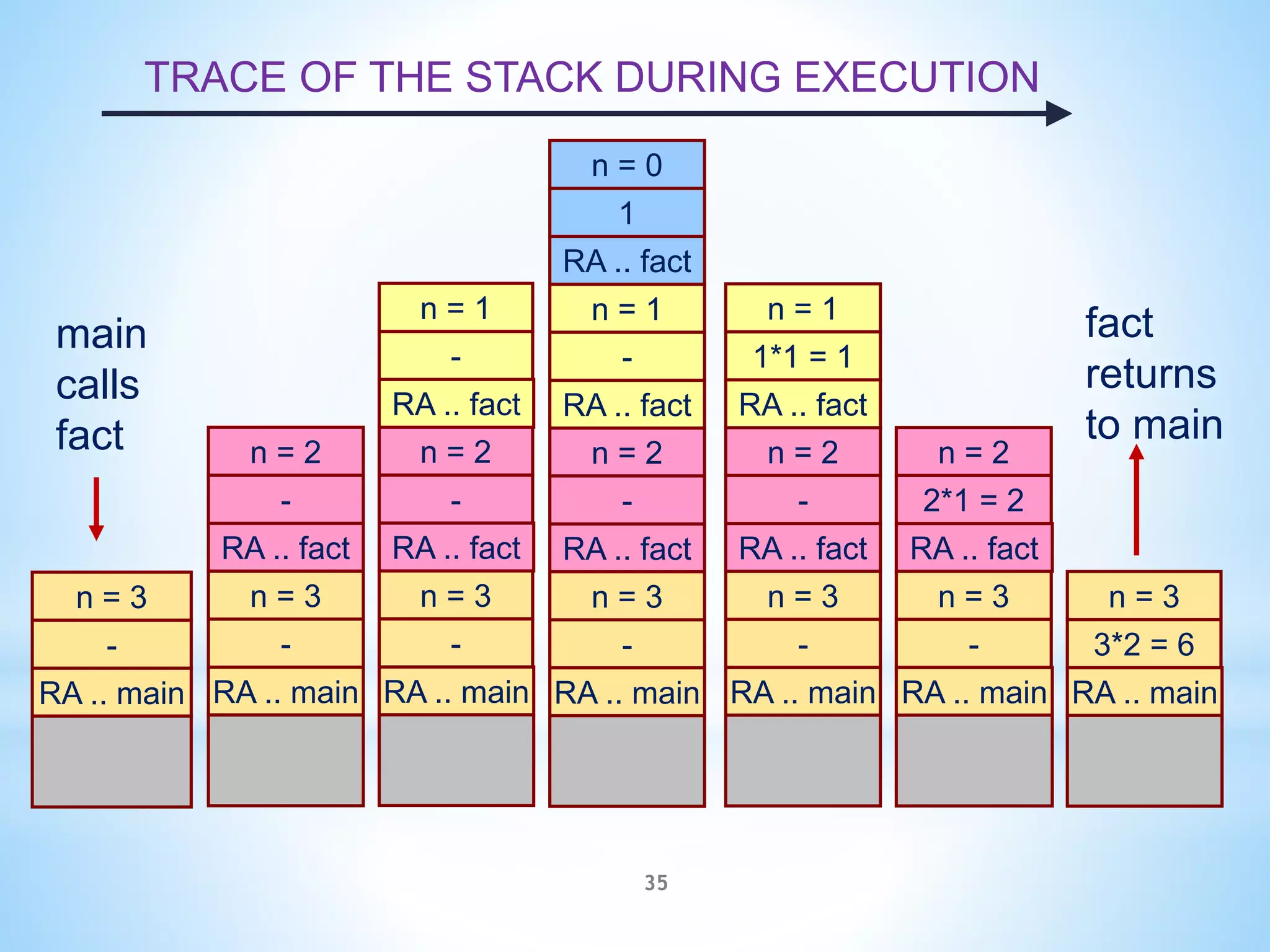
35
RA .. main
-
n = 3
RA .. main
-
n = 3
RA .. fact
-
n = 2
RA .. main
-
n = 3
RA .. fact
-
n = 2
RA .. fact
-
n = 1
RA .. main
-
n = 3
RA .. fact
-
n = 2
RA .. fact
-
n = 1
RA .. fact
1
n = 0
RA .. main
-
n = 3
RA .. fact
-
n = 2
RA .. fact
1*1 = 1
n = 1
RA .. main
-
n = 3
RA .. fact
2*1 = 2
n = 2
RA .. main
3*2 = 6
n = 3
TRACE OF THE STACK DURING EXECUTION
main
calls
fact
fact
returns
to main

36
Trace the activation records for the following version of Fibonacci
sequence.
?
#include <stdio.h>
int f (int n)
{
int a, b;
if (n < 2) return (n);
else {
a = f(n-1);
b = f(n-2);
return (a+b); }
}
main() {
printf(“Fib(4) is: %d n”, f(4));
}
Return Addr
(either main,
or X, or Y)
Return Value
Local
Variables
(n, a, b)
X
Y
main

Problems to Ponder…
38
1. Add a counter to count the number of function calls occurs in each of the sample recursive programs
discussed in this lecture slides.
2. If a local variable is defined in side the body of recursive function, what will happen to the values of that
variables?
3. Formulate each of the following algebraic formulas in recursive forms.
a) sum = a[0] + a[1] + a[2] + … + a[size], where a[size] is an array of integer with size size.
b) y = 1 − 𝑥 +
𝑥2
2!
−
𝑥3
3!
+
𝑥4
4!
−∙∙∙ −1 𝑛 𝑥𝑛
𝑛1
c) 𝑦 = 𝑥𝑛
, where x is any floating point number and n is a positive integer. Find the values of y using i)
iteration and ii) recursion
d) Find the product of n floating point numbers. The numbers should be read from the keyboard. You
should not use any looping construct. [Hint: use recursion and decide a suitable sentinel for
termination of recursion.]

06 Recursion in C.pptx

More Related Content

What's hot

Similar to 06 Recursion in C.pptx

More from MouDhara1

Recently uploaded

In this document

06 Recursion in C.pptx