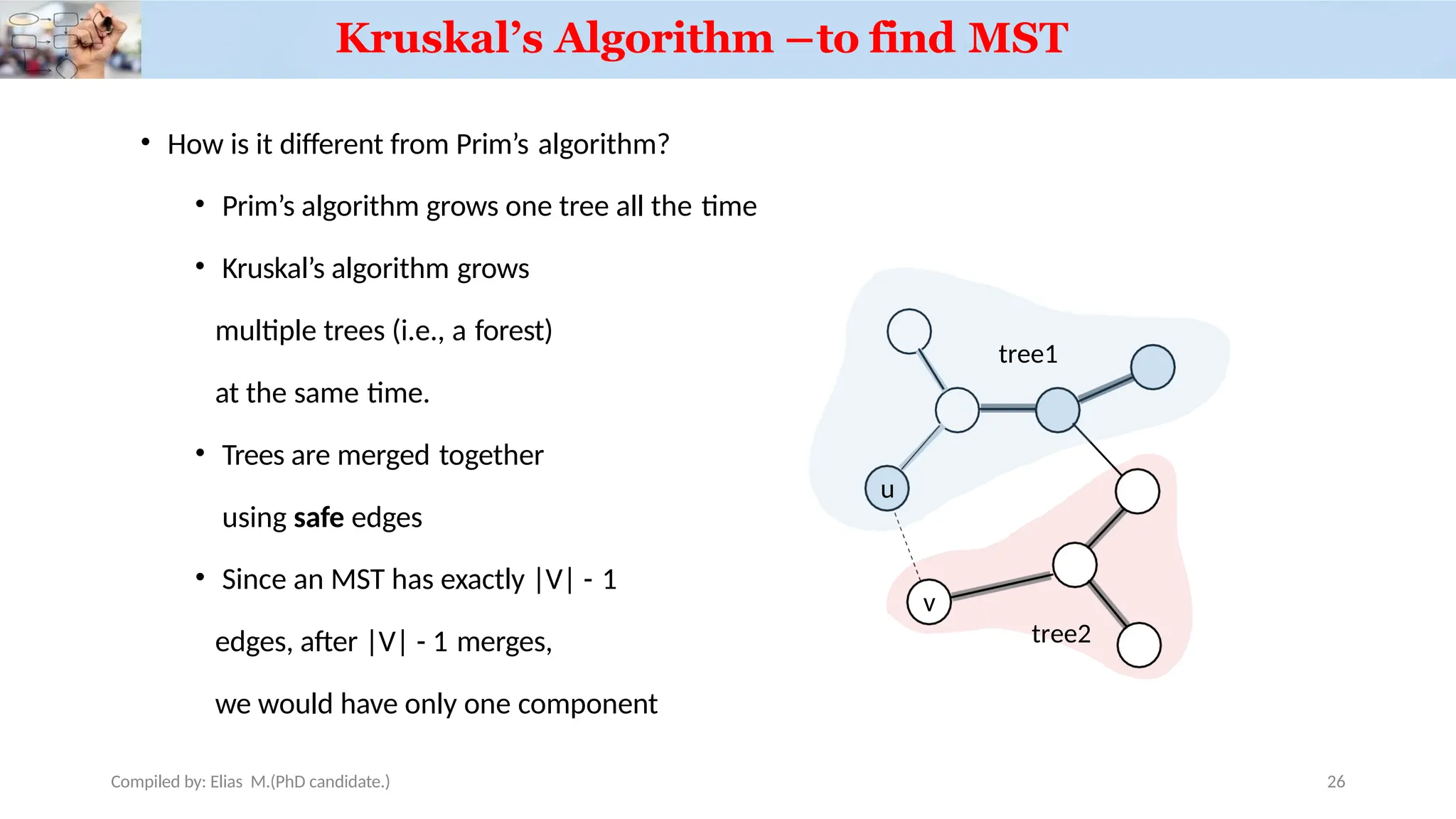
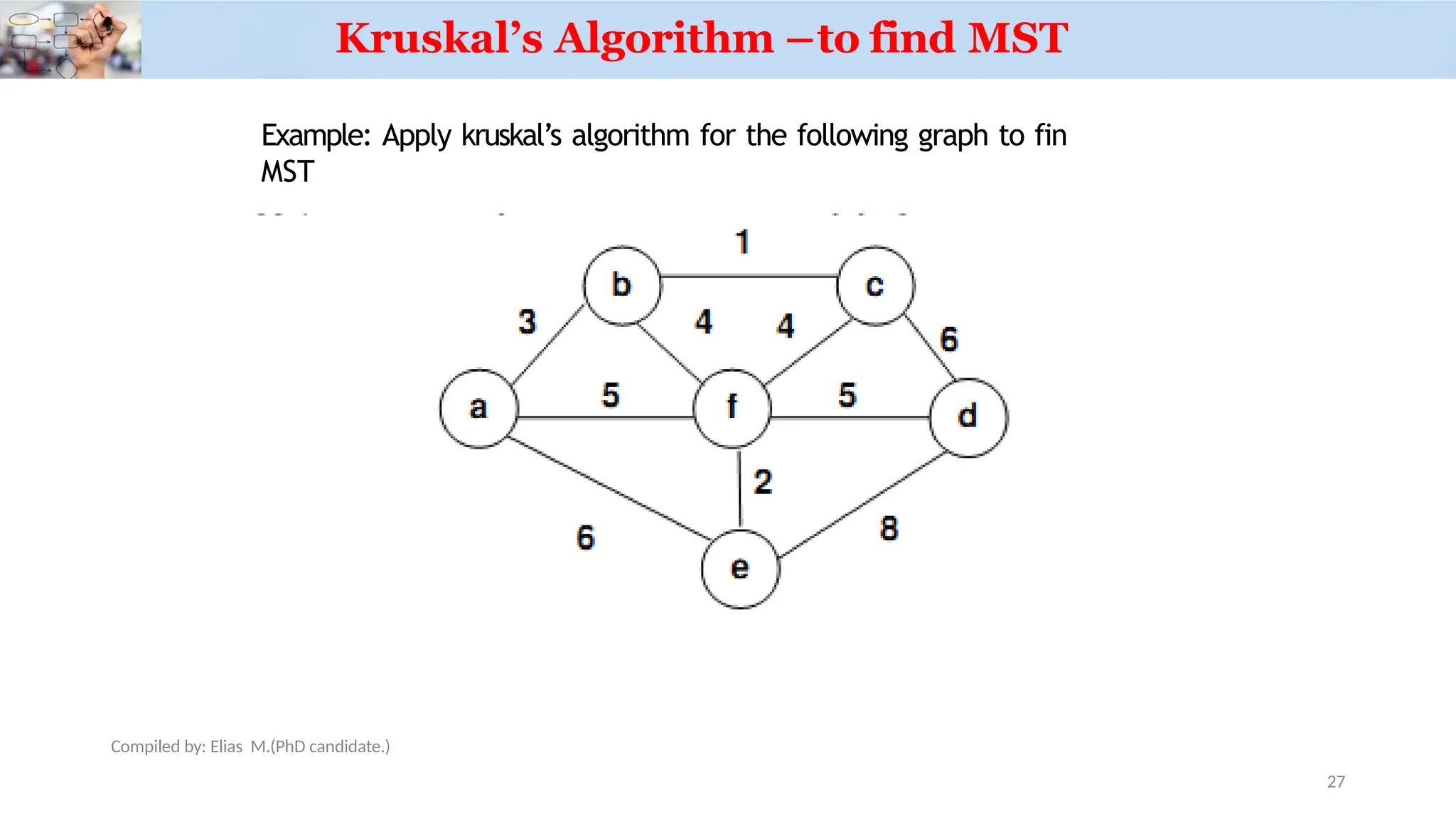
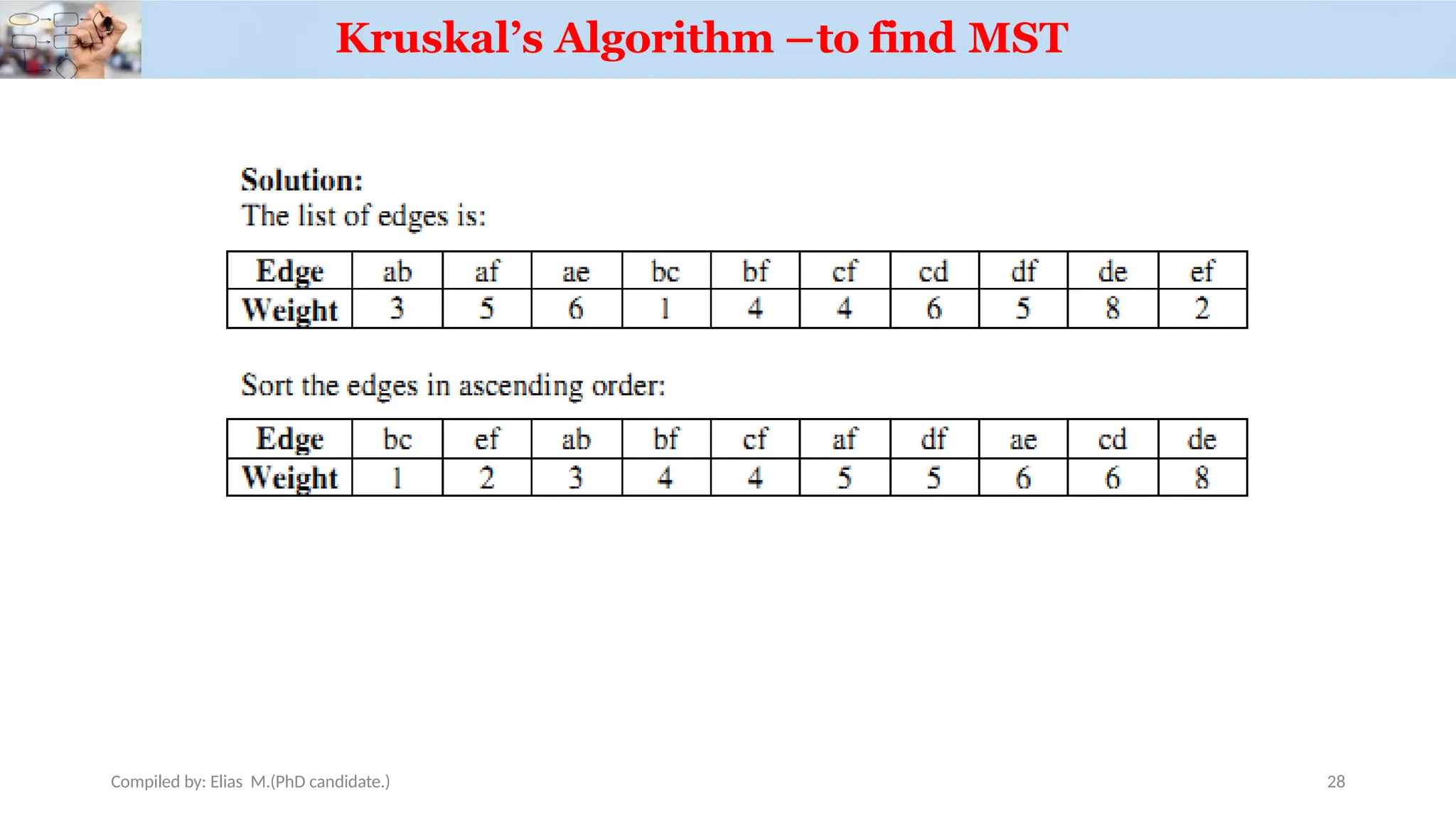
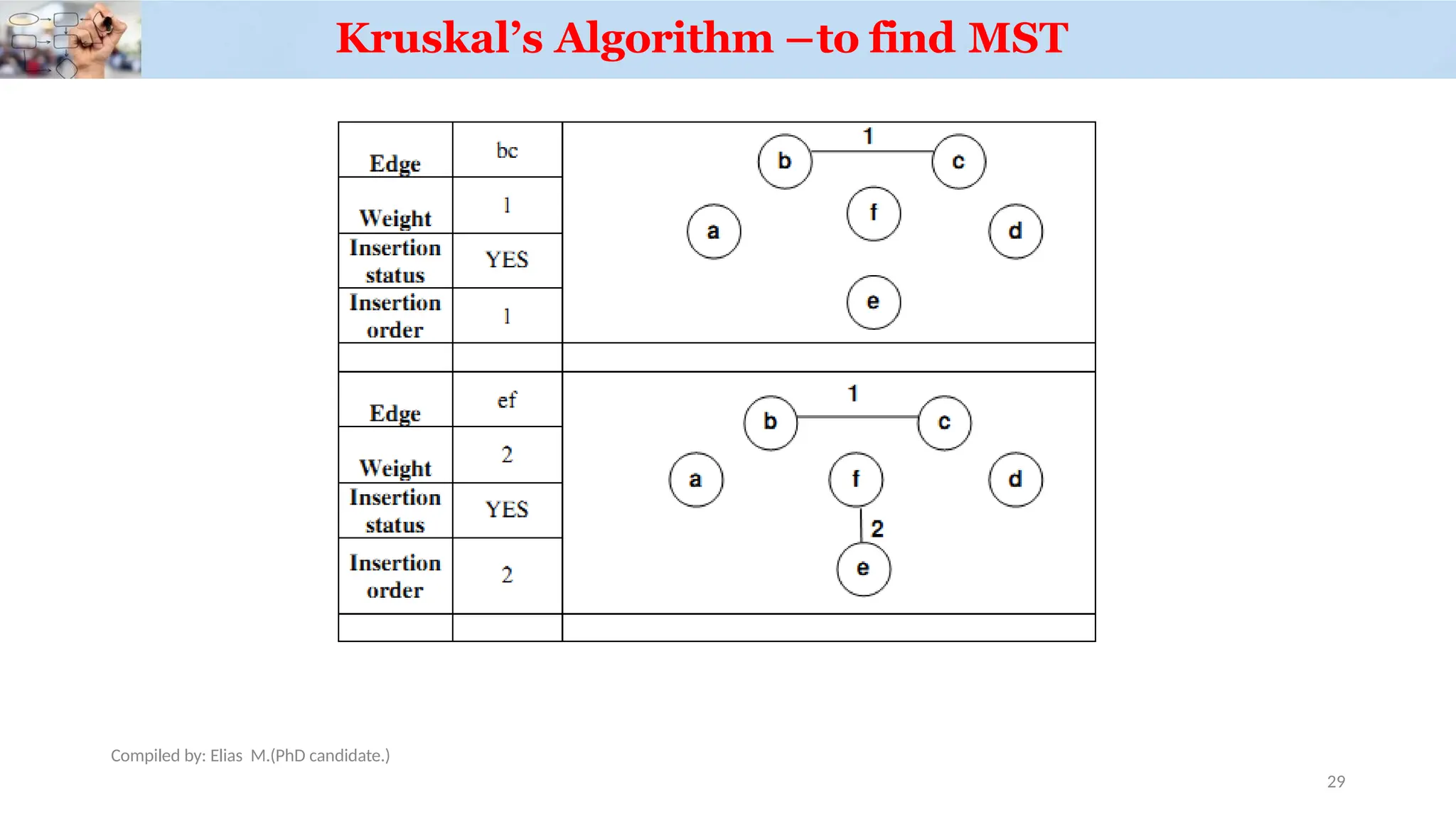
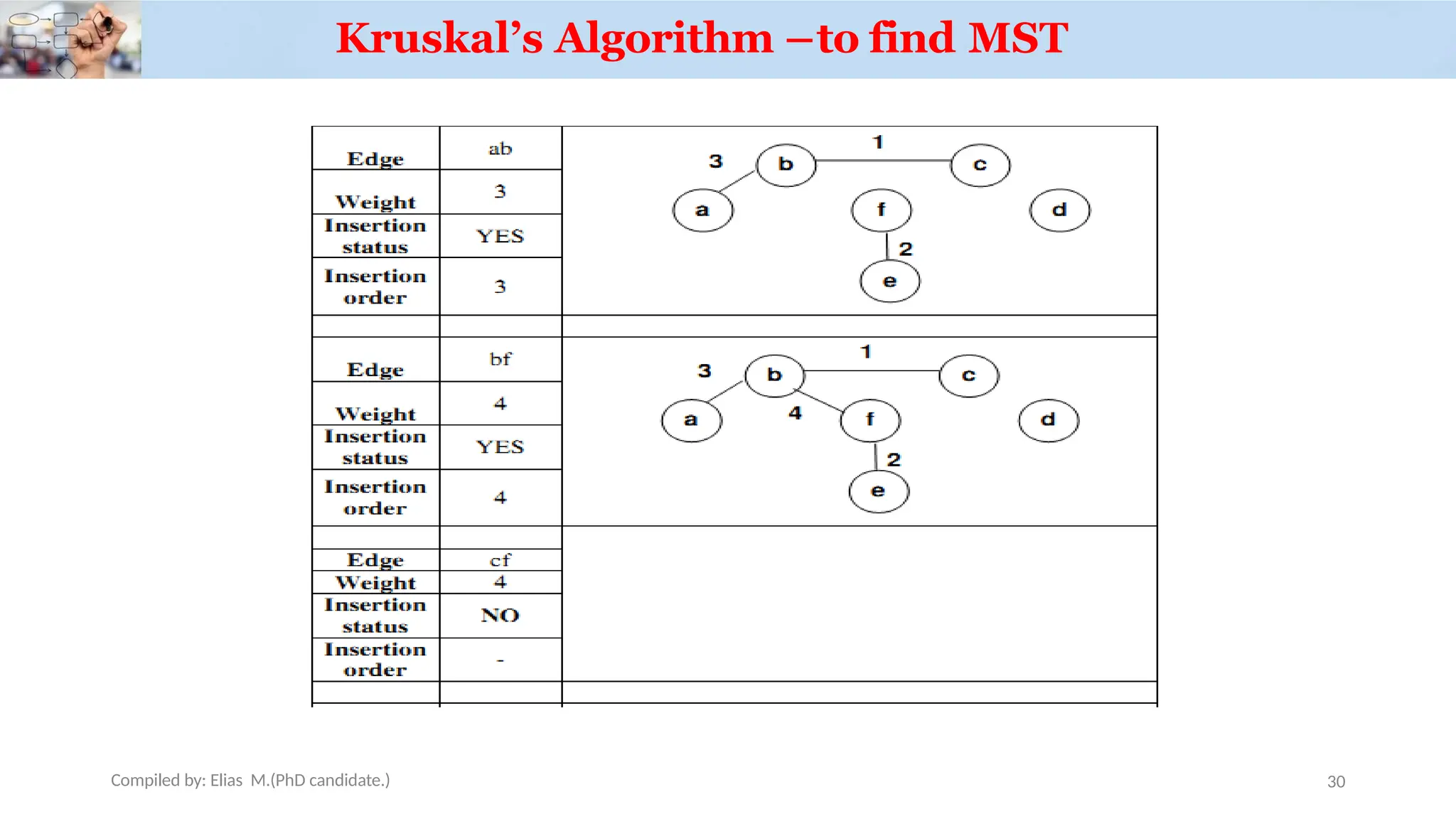
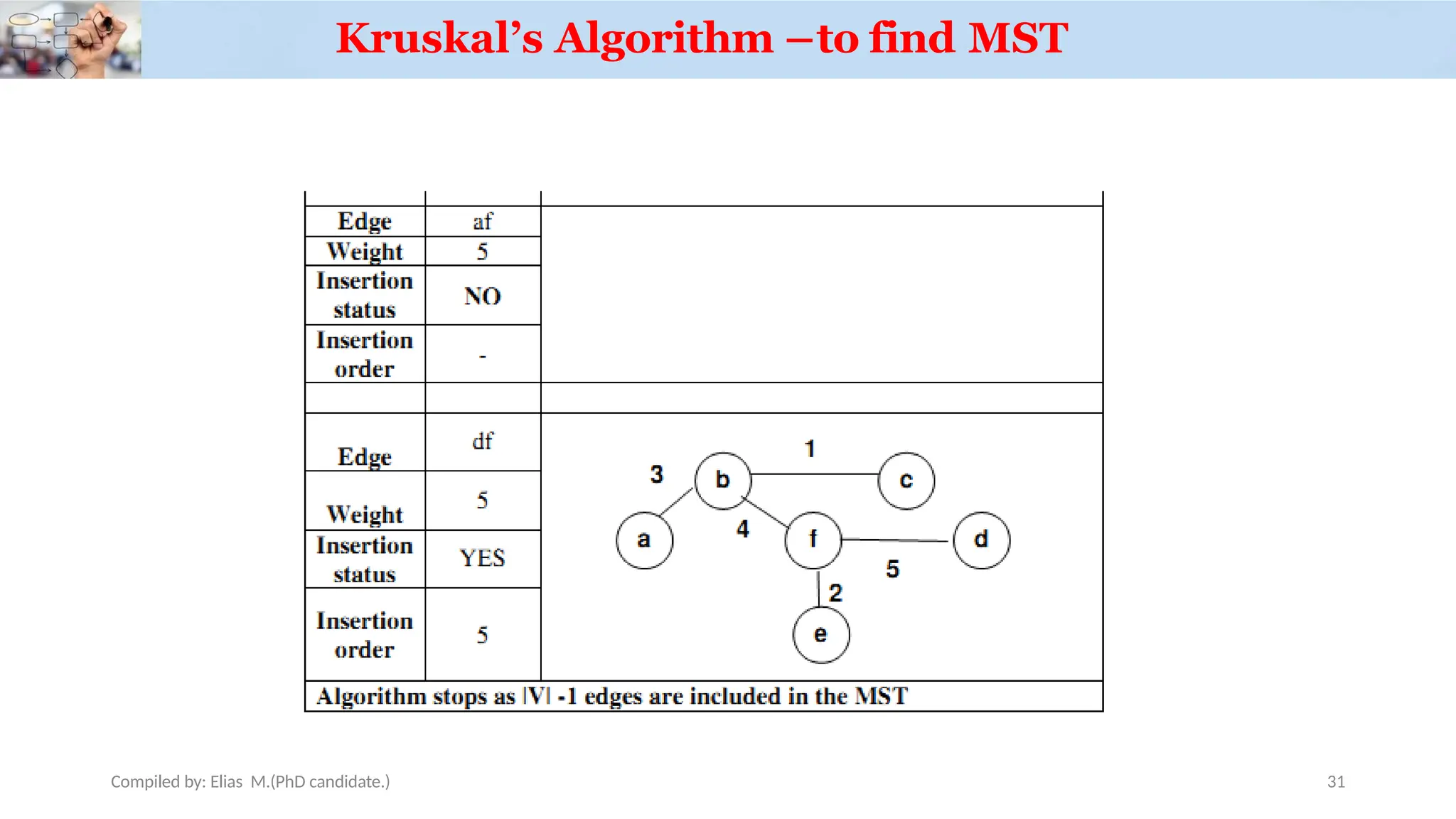
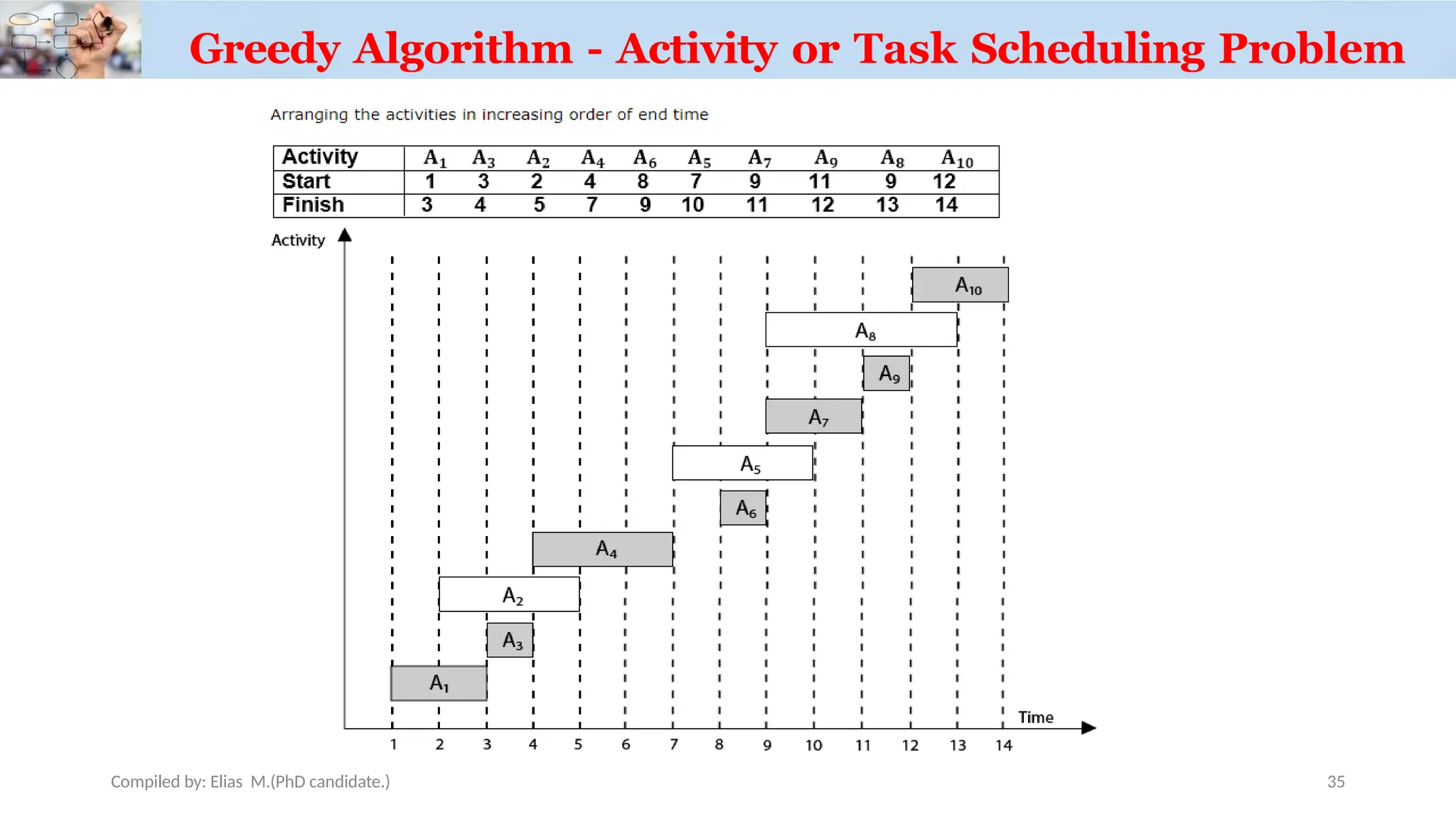
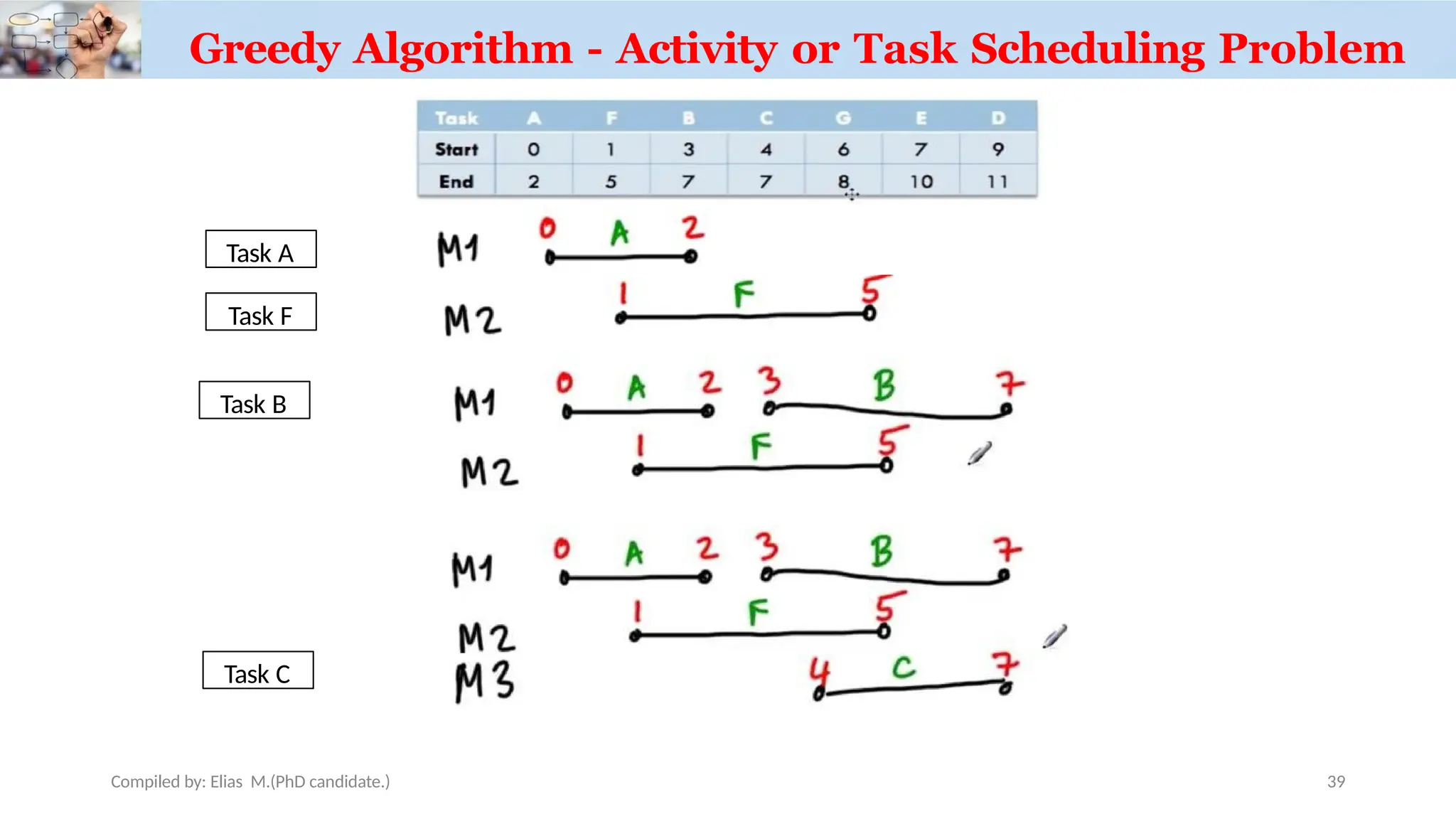
Chapter 3 discusses greedy algorithms, highlighting their role in solving optimization problems such as finding minimum spanning trees (MST) using Kruskal's and Prim's algorithms. It emphasizes the characteristics, applications of MST, and details the processes involved in both algorithms, including their efficiency. The document also touches on task scheduling problems as an application of greedy algorithms.



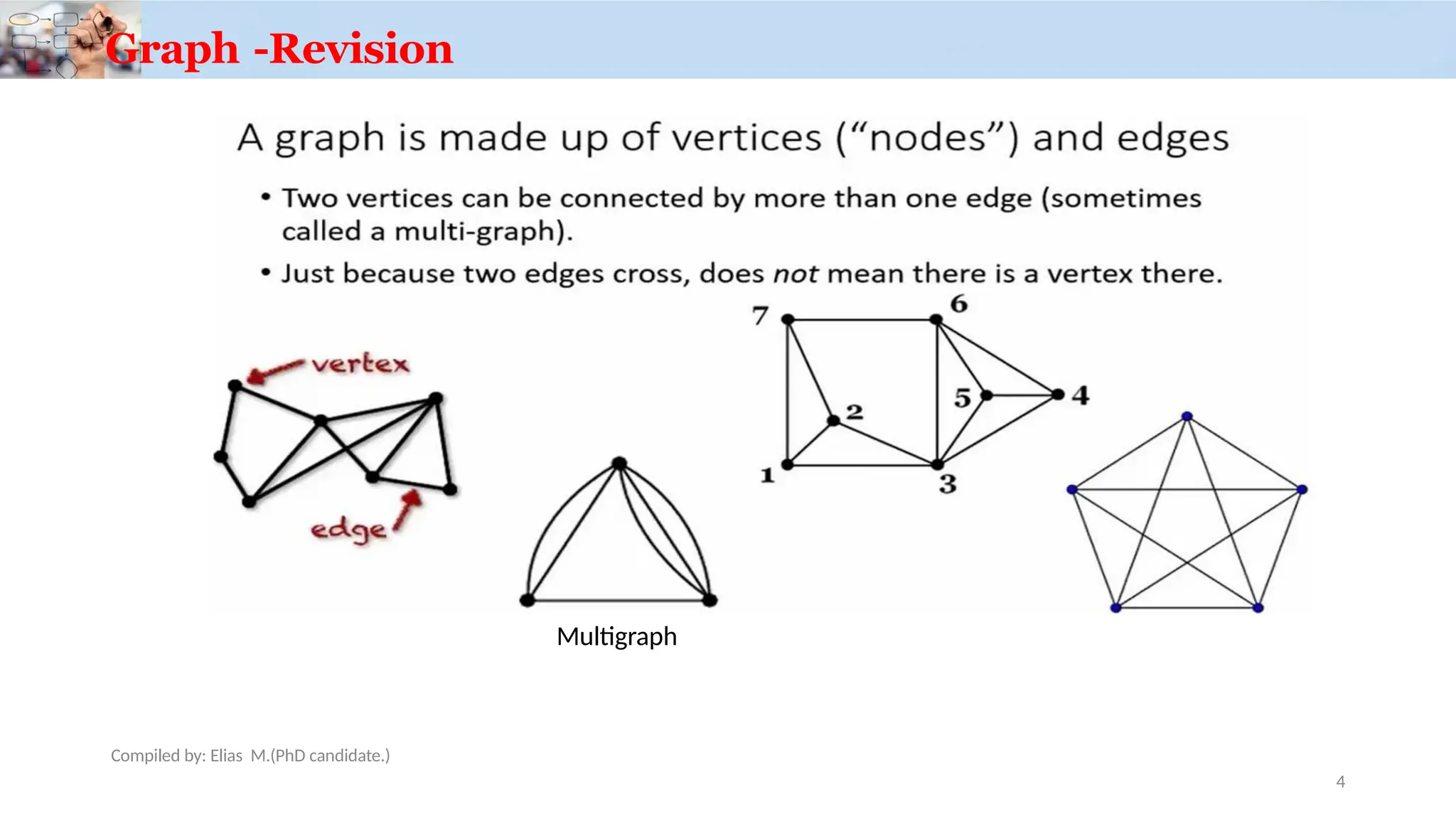

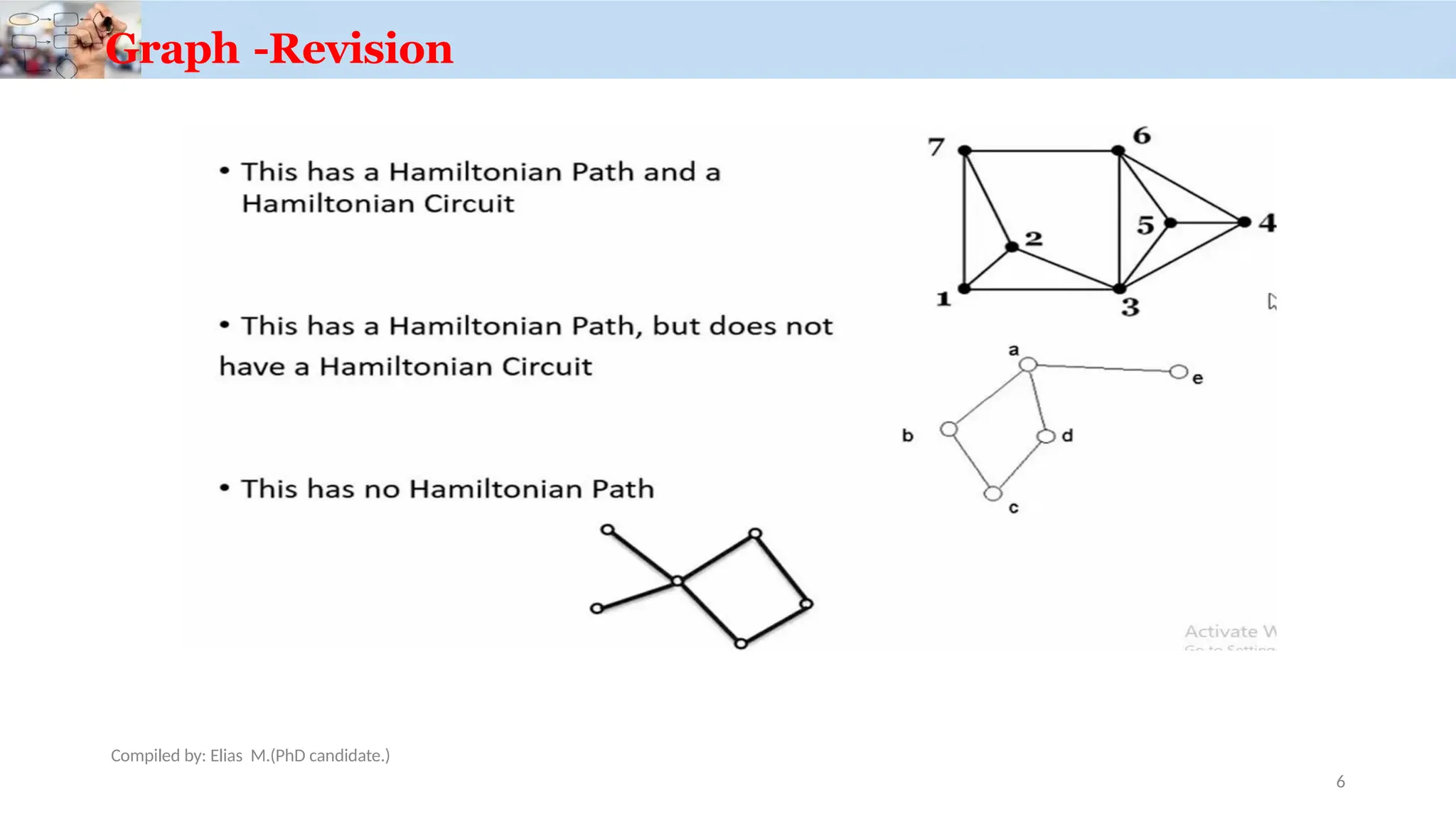



![How to Find Light Edges Quickly?
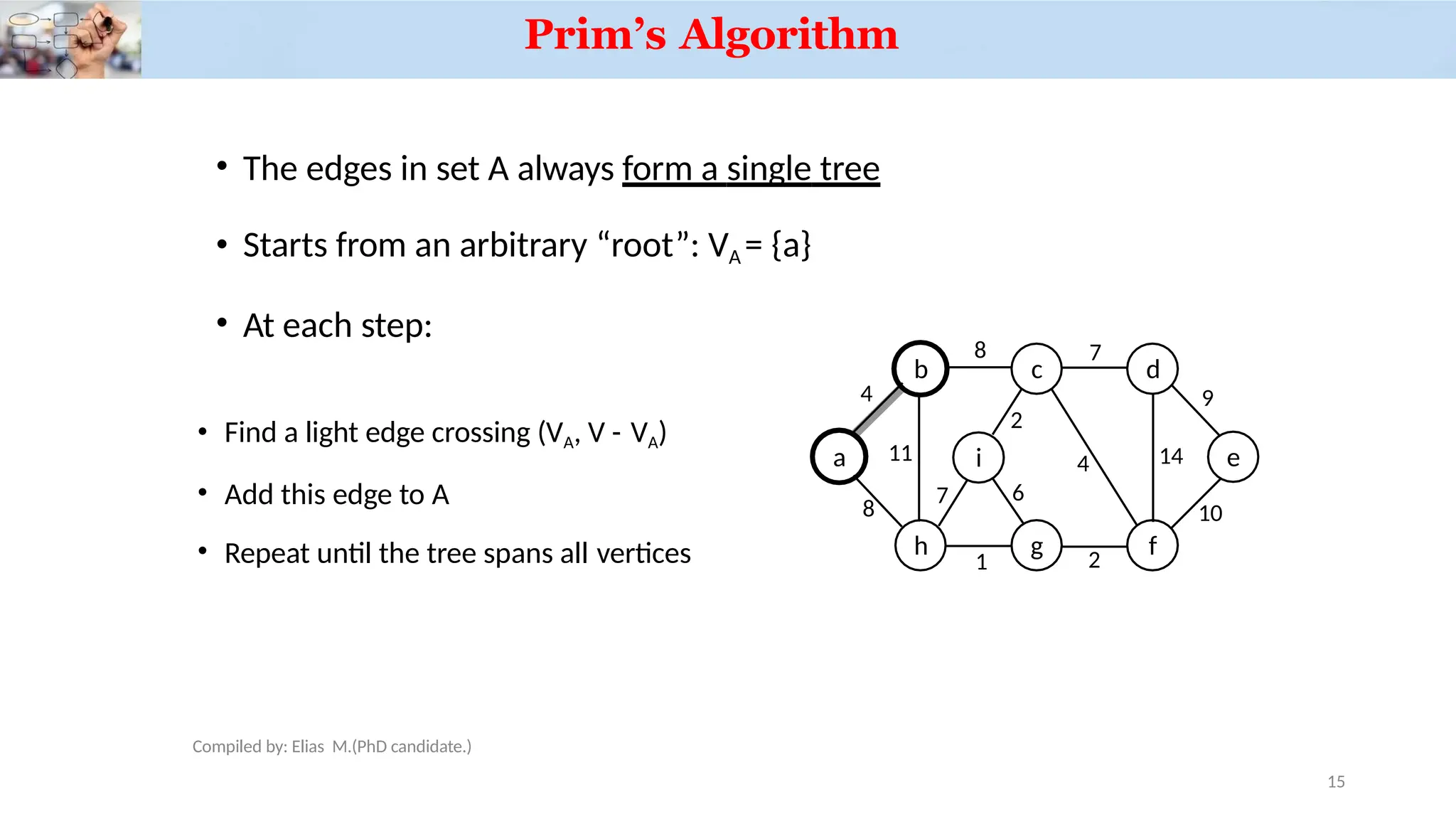
Use a priority queue Q:
• Contains vertices not yet
A
included in the tree, i.e., (V – V )
A
• V = {a}, Q = {b, c, d, e, f, g, h, i}
• We associate a key with each vertex v:
key[v] = minimum weight of any edge (u, v)
connecting v to VA
a
b c d
e
h g f
i
4
8 7
8
11
1 2
7
2
4 14
9
10
6
w1
w2
Key[a]=min(w1,w2)
a
17
Compiled by: Elias M.(PhD candidate.)](https://image.slidesharecdn.com/chapter3greedy1-240902103849-1552b2f0/75/Algorithm-analysis-Greedy-method-in-algorithm-pptx-17-2048.jpg)
![How to Find Light Edges Quickly? (cont.)
• After adding a new node to VAwe update the weights of all the
nodes adjacent to it
e.g., after adding a to the tree, k[b]=4 and k[h]=8
• Key of v is if v is not adjacent to any vertices in VA
a
b c d
e
h g f
i
4
8 7
8
11
1 2
7
2
4 14
9
10
6
18
Compiled by: Elias M.(PhD candidate.)](https://image.slidesharecdn.com/chapter3greedy1-240902103849-1552b2f0/75/Algorithm-analysis-Greedy-method-in-algorithm-pptx-18-2048.jpg)
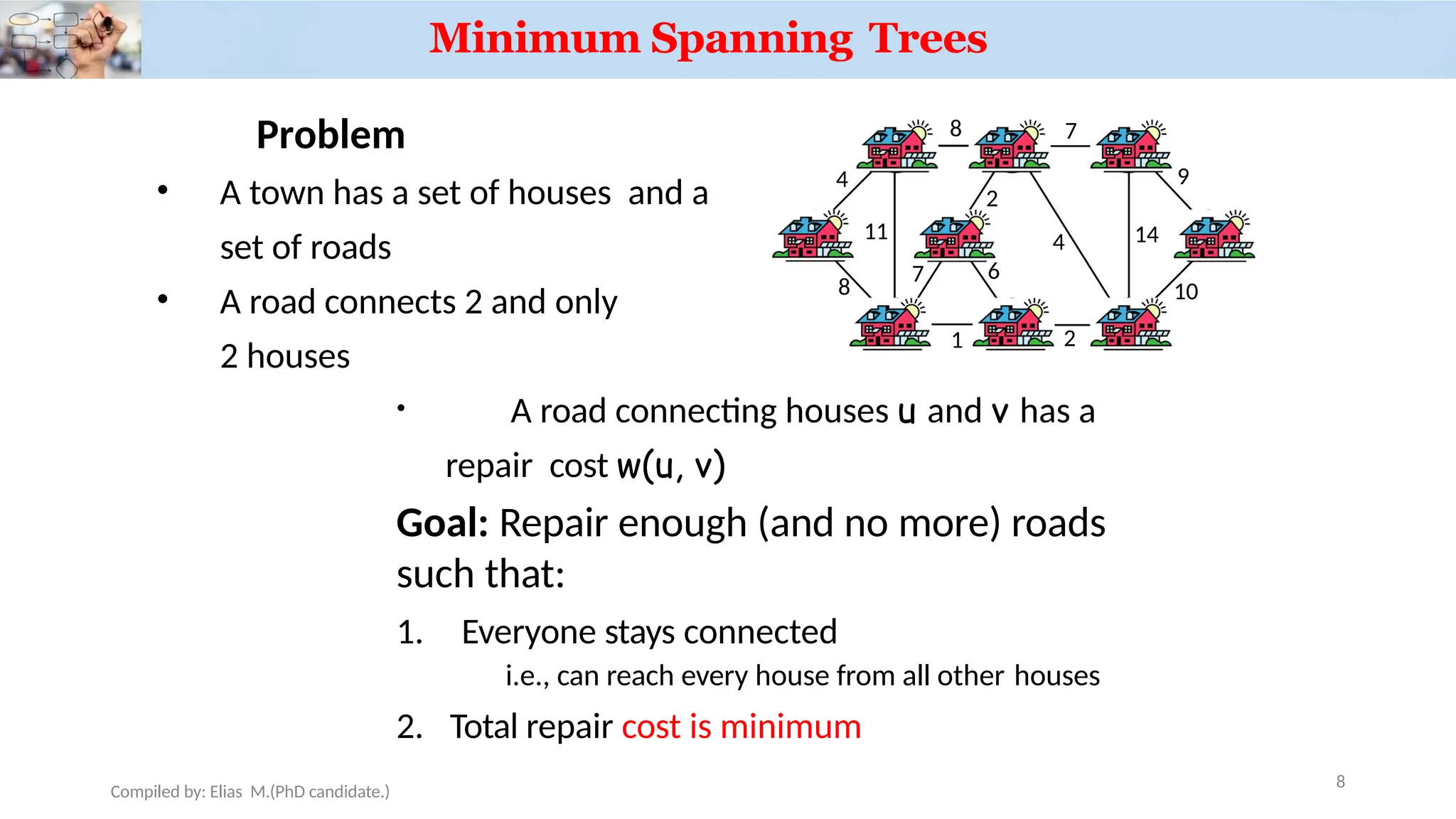
![Example
0 Q =
{a, b, c, d, e, f, g, h, i} VA
=
Extract-MIN(Q) a
a
4
8 7
8
11
1 2
7
2
4 14
10
6
b
c
d
i
9
e
h
g
f
a
b
h
4
8 7
8
11
1 2
7
2
4 14
9
10
6
c
d
i
e
g
f
key [b] = 4 [b] =
a
[h] =
a
key [h] = 8
4 8
Q = {b, c, d, e, f, g, h, i} VA = {a}
Extract-MIN(Q) b
4
8
Compiled by: Elias M.(PhD candidate.)
19](https://image.slidesharecdn.com/chapter3greedy1-240902103849-1552b2f0/75/Algorithm-analysis-Greedy-method-in-algorithm-pptx-19-2048.jpg)
![
Example
a
c
4
8 7
8
11
1 2
7
2
4 14
9
10
6
key [c] = 8 [c] = b
[h] = a -
unchanged
key [h] = 8
8 8
A
Q = {c, d, e, f, g, h, i} V = {a,
b}
Extract-MIN(Q) c
a
d
h
8
g
f
i
4
8 7
8
11
1 2
7
2
4 14
9
e
10
6
key [d] = 7
key [f] =
4 key [i] =
2
[d] =
c
[f] =
c
[i] =
c
7 4 8 2
Q = {d, e, f, g, h, i} VA= {a, b, c}
Extract-MIN(Q) i
i
4
b
d
e
h
8
4
b
g
8
c
f
8
7
4
2
Compiled by: Elias M.(PhD candidate.) 20](https://image.slidesharecdn.com/chapter3greedy1-240902103849-1552b2f0/75/Algorithm-analysis-Greedy-method-in-algorithm-pptx-20-2048.jpg)
![Example
a
4
8 7
8
11
1 2
7
2
4 14
10
6
key [h] = 7
key [g] = 6
[h] =
i
[g] =
i
7 4 6 8
Q = {d, e, f, g, h} V = {a, b, c,
i}
A
Extract-MIN(Q) f
a
b c d
h g f
4
8 7
8
11
1 2
7
2
4 14
9
10
6
4
b
7
d
9
e
key [g] = 2
key [d] = 7
key [e] = 10
7 10 2
8
[g] = f
[d] = c
unchanged
[e] = f
Q = {d, e, g, h} V = {a, b, c, i,
f}
A
Extract-MIN(Q)
g
8
f
4
8
c
2
i
h
7
4 7
g
6
8
2
i
10
e
6 4
7 2
Compiled by: Elias M.(PhD candidate.) 21](https://image.slidesharecdn.com/chapter3greedy1-240902103849-1552b2f0/75/Algorithm-analysis-Greedy-method-in-algorithm-pptx-21-2048.jpg)
![Example
a
b c d
h
4
8 7
8
11
1 2
7
4 14
10
6
key [h] = 1 [h] =
g
7 10 1
Q = {d, e, h} V = {a, b, c, i, f,
g}
A
Extract-MIN(Q)
h
a
c
h g f
4
8 7
8
11
1 2
7
4 14
10
6
9
10
e
7 10
Q = {d, e} VA= {a, b, c, i, f, g, h}
Extract-MIN(Q) d
4 7
7
2 2
i
8
1
4
2
1
Compiled by: Elias M.(PhD candidate.)
22
4
b
f
4
7
d
9
10
e
g
2
8
2 2
i](https://image.slidesharecdn.com/chapter3greedy1-240902103849-1552b2f0/75/Algorithm-analysis-Greedy-method-in-algorithm-pptx-22-2048.jpg)
![Example
a
b c d
e
4
8 7
8
11
1 2
7
2
4 14
9
10
6
key [e] = 9 [e] =
f
9
Q = {e} V = {a, b, c, i, f, g, h,
d}
A
Extract-MIN(Q) e
Q = VA= {a, b, c, i, f, g, h, d, e}
4 7
10
h
1
g
2
f
4
2
i
8
9
Compiled by: Elias M.(PhD candidate.) 23](https://image.slidesharecdn.com/chapter3greedy1-240902103849-1552b2f0/75/Algorithm-analysis-Greedy-method-in-algorithm-pptx-23-2048.jpg)
![PRIM(V, E, w, r)
3.
4.
5.
1. Q ←
2. for each u V
do key[u] ← ∞
π[u] ← NIL
INSERT(Q, u)
6. DECREASE-KEY(Q, r, 0)
7. while Q
► key[r] ← 0
8. do u ← EXTRACT-MIN(Q)
for each v Adj[u]
do if v Q and
w(u, v) < key[v]
then π[v] ←
u
9.
10.
11.
12. DECREASE-KEY(Q, v, w(u, v))
O(V) if Q is implemented as
a min-heap
Executed |V| times
Takes O(lgV)
O(lgV)
Min-heap
operations
: O(VlgV)
Executed O(E) times total
Constant
Takes O(lgV)
O(ElgV)
Total time: O(VlogV + ElogV) = O(ElogV)
Compiled by: Elias M.(PhD candidate.)
24](https://image.slidesharecdn.com/chapter3greedy1-240902103849-1552b2f0/75/Algorithm-analysis-Greedy-method-in-algorithm-pptx-24-2048.jpg)