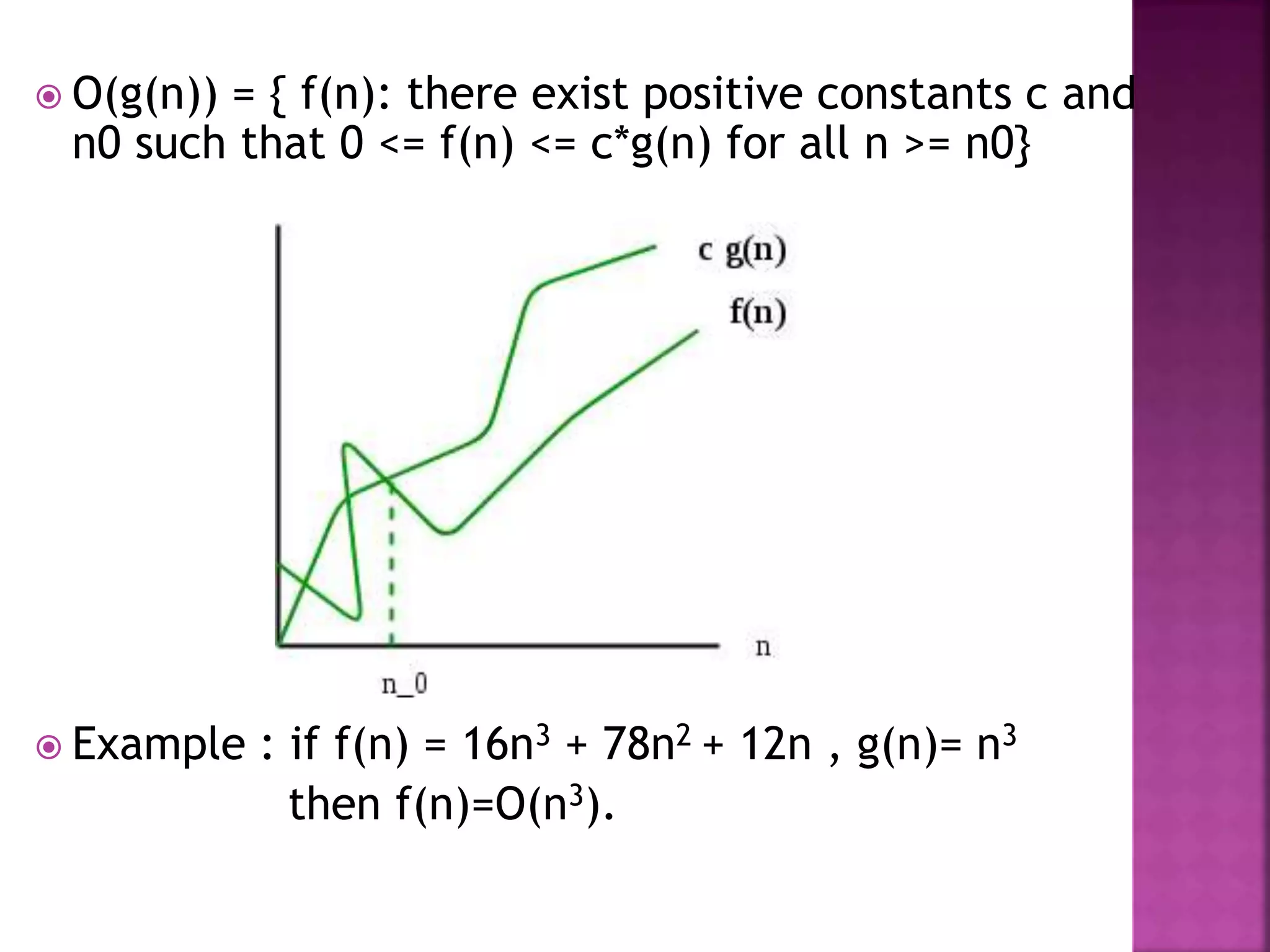
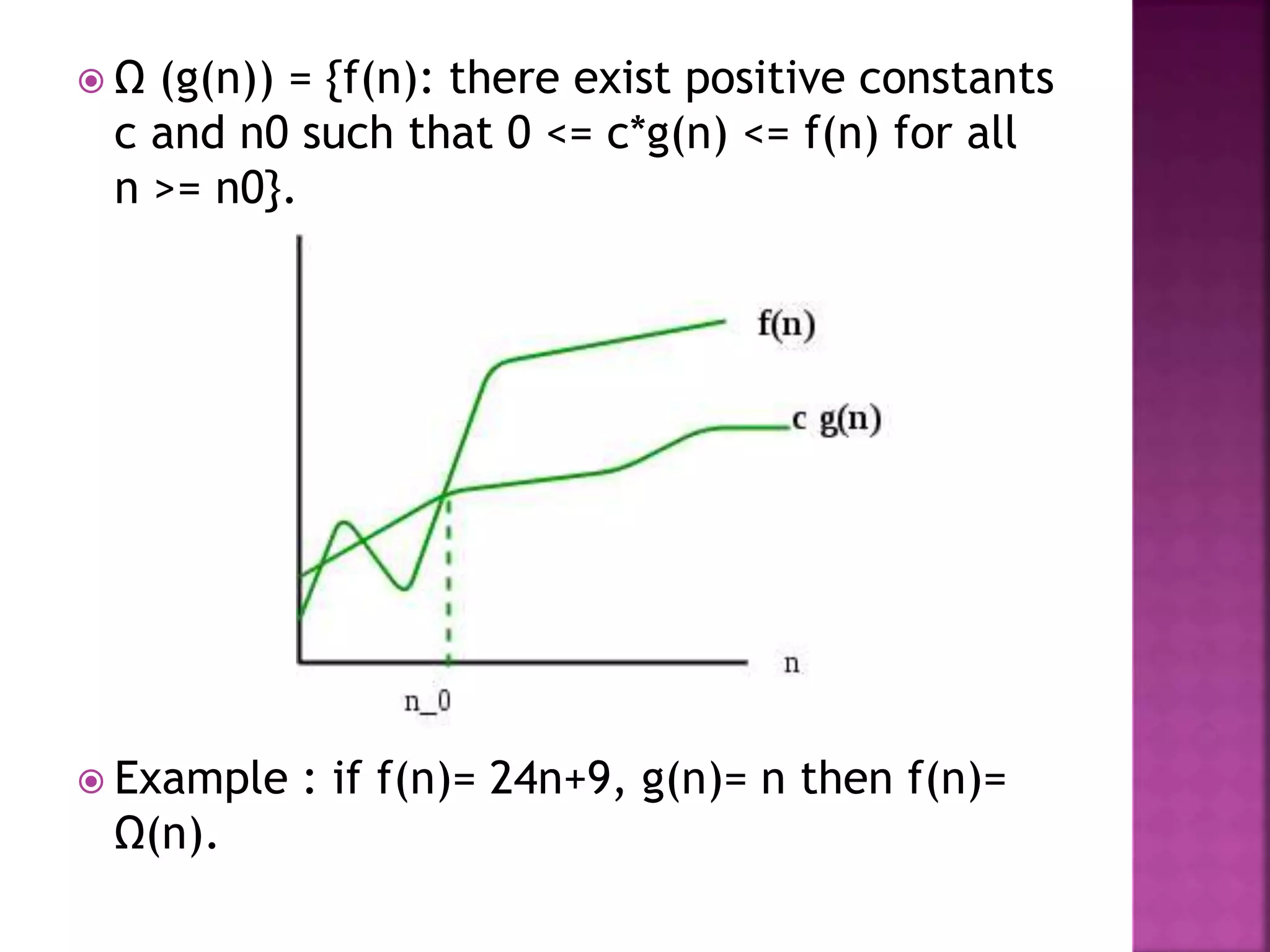
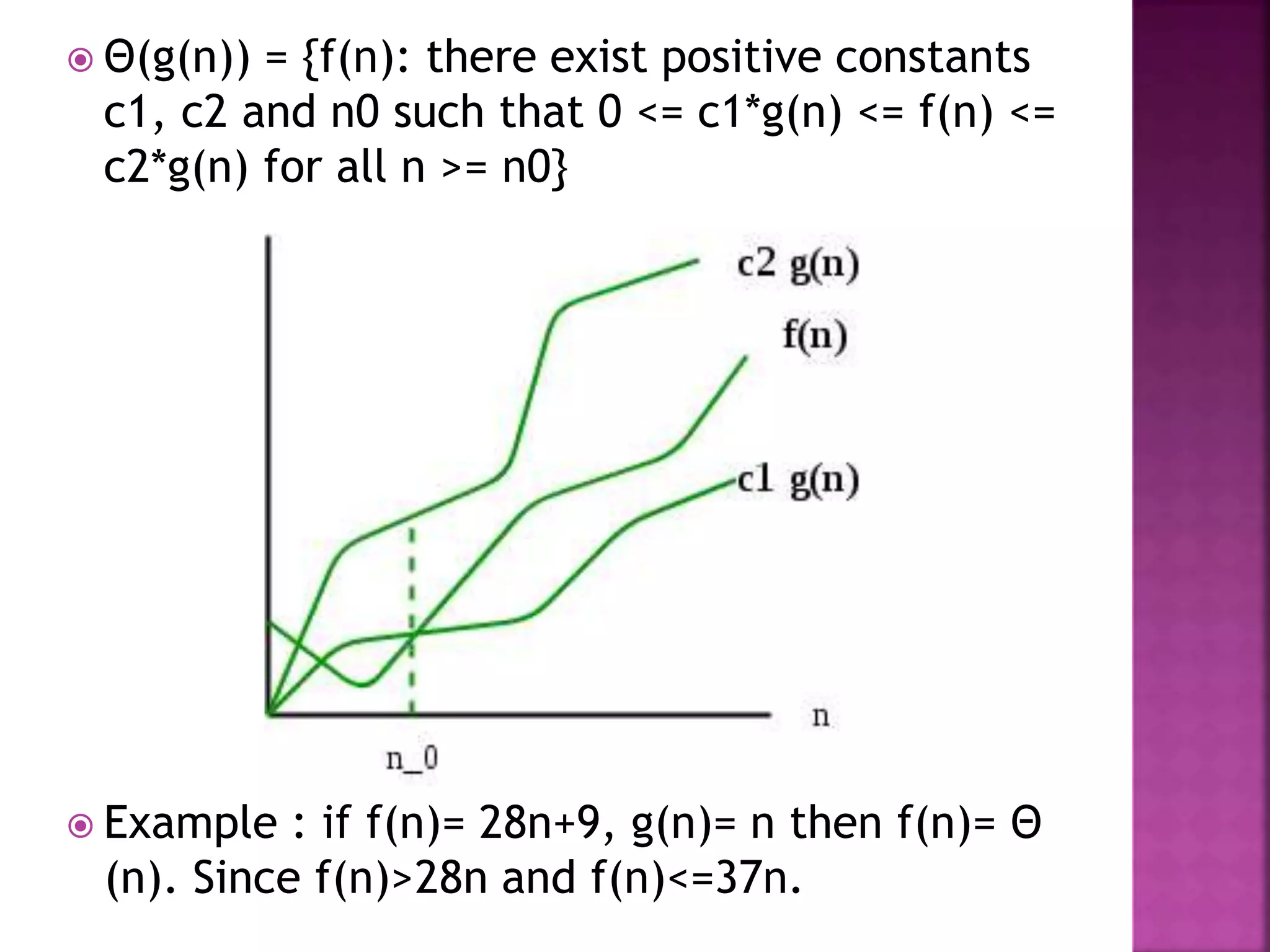
This document discusses algorithms, their properties, and performance analysis focusing on time and space complexity. It covers both posteriori and apriori analysis methods, as well as asymptotic analysis using notations such as ο, ω, θ, and their significance in measuring algorithm efficiency. Additionally, it provides examples and definitions to illustrate time complexity in different scenarios, including best, average, and worst cases.