Automata theory - NFA ε to DFA Conversion

Convert the given NFA-ε into its equivalent DFA.
• Solution:
Let us obtain the ε-closure of each state.
ε-closure(q0) = {q0, q1, q2}
ε-closure(q1) = {q1, q2}
ε-closure(q2) = {q2}
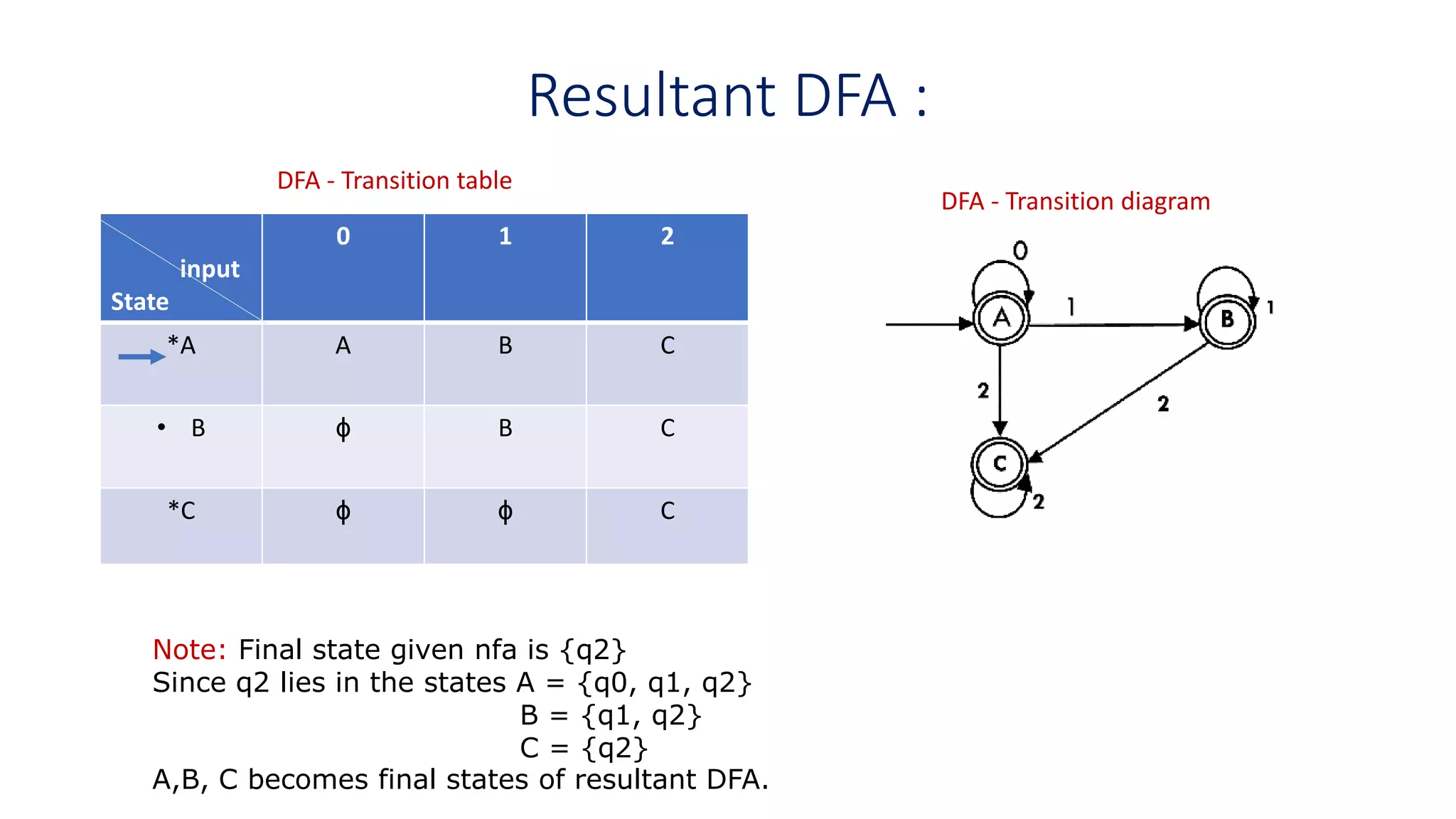
Let the initial state of DFA be ε-closure(q0) = {q0, q1, q2}
= [q0, q1, q2] ----- A.

Find transitions of A on inputs 0,1,2
δ'(A, 0) = ε-closure{δ((q0, q1, q2), 0)}
= ε-closure{δ(q0, 0) ∪ δ(q1, 0) ∪ δ(q2, 0)}
= ε-closure{q0}
= {q0, q1, q2}
=[q0, q1, q2] ----- A
δ'(A, 1) = ε-closure{δ((q0, q1, q2), 1)}
= ε-closure{δ(q0, 1) ∪ δ(q1, 1) ∪ δ(q2, 1)}
= ε-closure{q1}
= {q1, q2}
= [q1, q2] ------- B
δ'(A, 2) = ε-closure{δ((q0, q1, q2), 2)}
= ε-closure{δ(q0, 2) ∪ δ(q1, 2) ∪ δ(q2, 2)}
= ε-closure{q2}
= {q2}
= [q2] ---------C

Find transitions of B on inputs 0,1,2
δ'(B, 0) = ε-closure{δ((q1, q2), 0)}
= ε-closure{δ(q1, 0) ∪ δ(q2, 0)}
= ε-closure{ϕ}
= ϕ ------- ϕ
δ'(B, 1) = ε-closure{δ((q1, q2), 1)}
= ε-closure{δ(q1, 1) ∪ δ(q2, 1)}
= ε-closure{q1}
= {q1, q2}
= [q1, q2] ------- B
δ'(B, 2) = ε-closure{δ((q1, q2), 2)}
= ε-closure{δ(q1, 2) ∪ δ(q2, 2)}
= ε-closure{q2}
= {q2}
= [q2] ------- C

Find transition of C on inputs 0,1,2
δ'(C, 0) = ε-closure{δ(q2, 0)}
= ε-closure{ϕ}
= ϕ ------- ϕ
δ '(C, 1) = ε-closure{δ(q2, 1)}
= ε-closure{ϕ}
= ϕ ------- ϕ
δ'(C, 2) = ε-closure{δ(q2, 2)}
= {q2}
= [q2] ------- C

Resultant DFA :
input
State
0 1 2
*A A B C
• B ϕ B C
*C ϕ ϕ C
Note: Final state given nfa is {q2}
Since q2 lies in the states A = {q0, q1, q2}
B = {q1, q2}
C = {q2}
A,B, C becomes final states of resultant DFA.
DFA - Transition table
DFA - Transition diagram

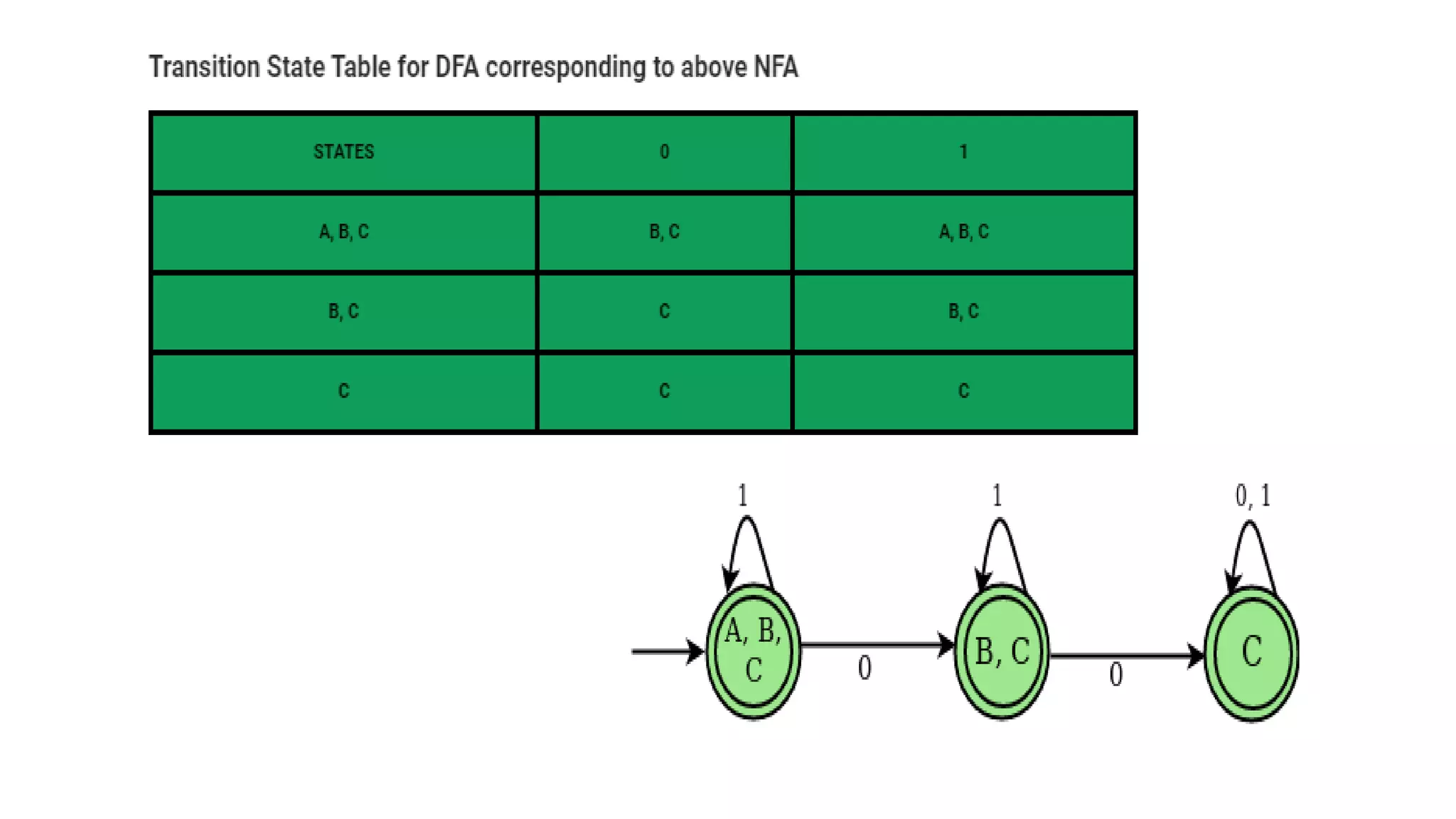
Example :2 Convert it to DFA
δ’(Z, 1)=ε-closure{δ((C), 1)} = [C] ----------Z
δ’(X, 0)=ε-closure{δ((A,B,C), 0)} = [B,C] -------- Y
δ’(X, 1)=ε-closure{δ((A,B,C), 1)} = [A,B,C] ----- X
δ’(Y, 0)=ε-closure{δ((B,C), 0)} = [C] ---------Z
δ’(Y, 1)=ε-closure{δ((B,C), 1)} = [B,C] ------Y
δ’(Z, 0)=ε-closure{δ((C), 0)} = [C] -----------Z
Let the initial state of DFA be ε-closure(A) = {A,B,C}
= [A,B,C] ----- X

Automata theory - NFA ε to DFA Conversion

Automata theory - NFA ε to DFA Conversion

More Related Content

What's hot

Similar to Automata theory - NFA ε to DFA Conversion

More from Akila Krishnamoorthy

Recently uploaded

Automata theory - NFA ε to DFA Conversion