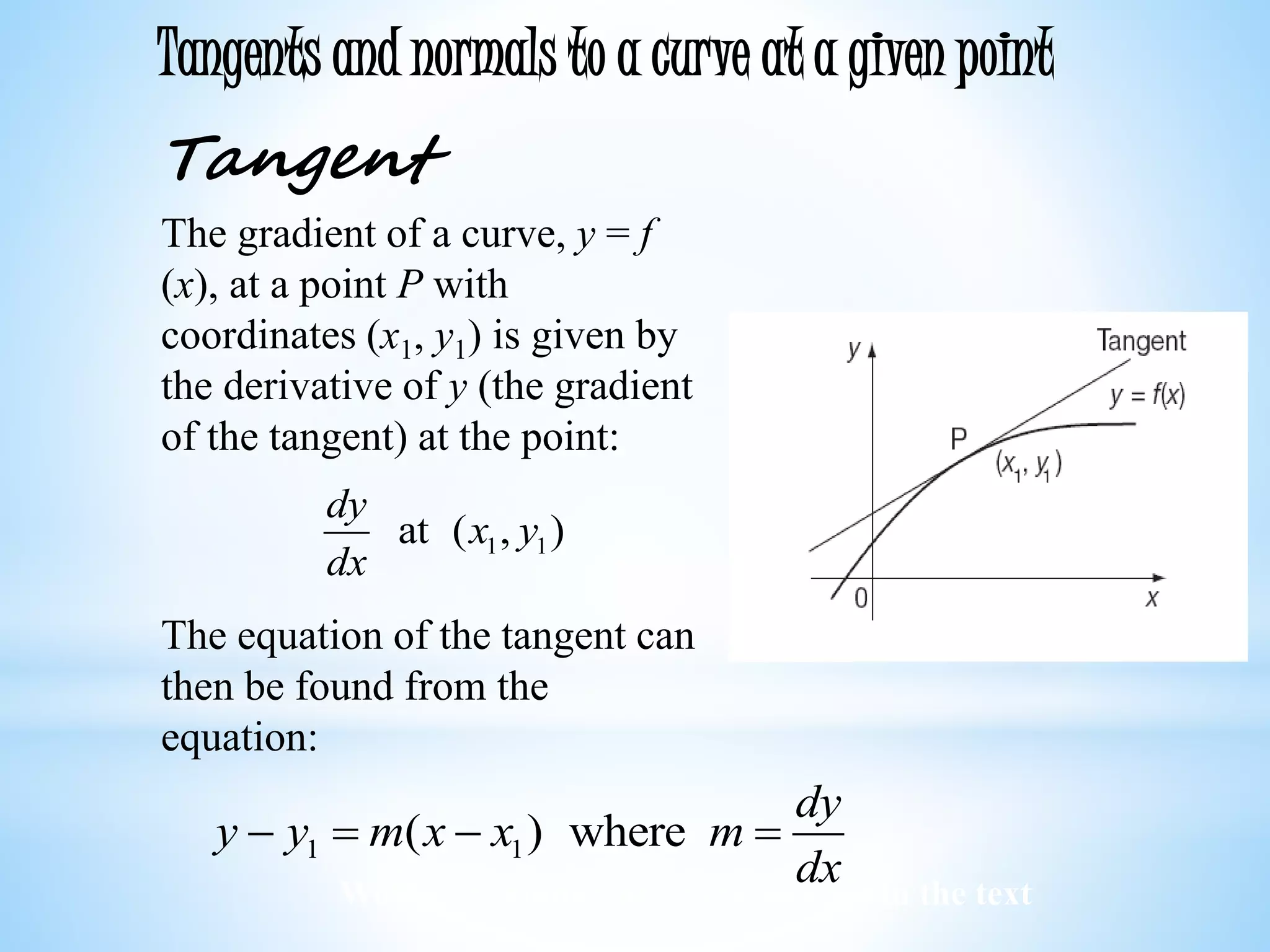
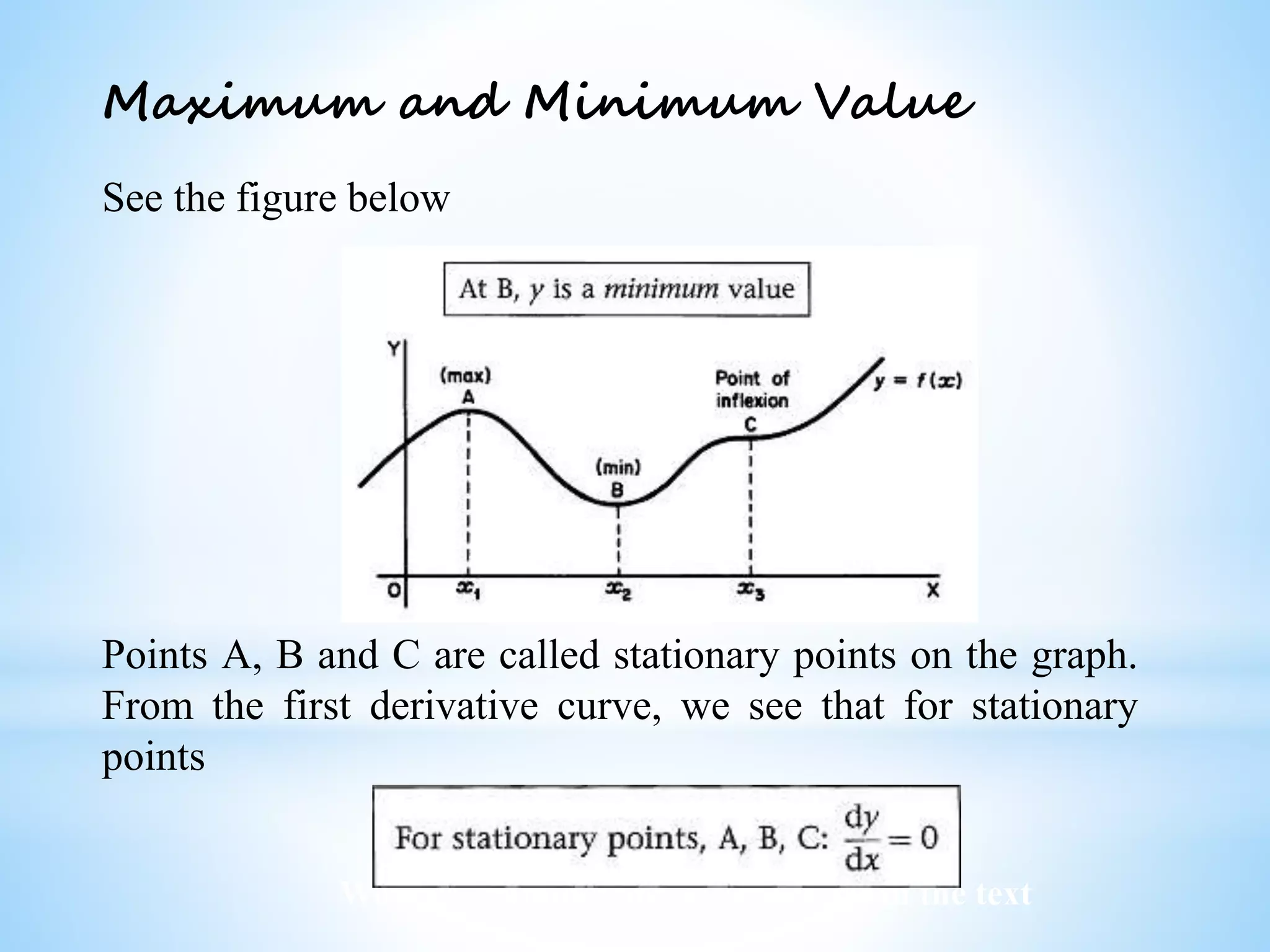
The document discusses differentiation applications, focusing on tangents and normals to curves, including the use of derivatives to find their equations. It also covers concepts of stationary points, maximum and minimum values, and L'Hôpital's Rule for limit forms, alongside worked examples and exercises related to economic functions like total revenue and profit. Additionally, it addresses identifying inflection points and the conditions under which they occur.