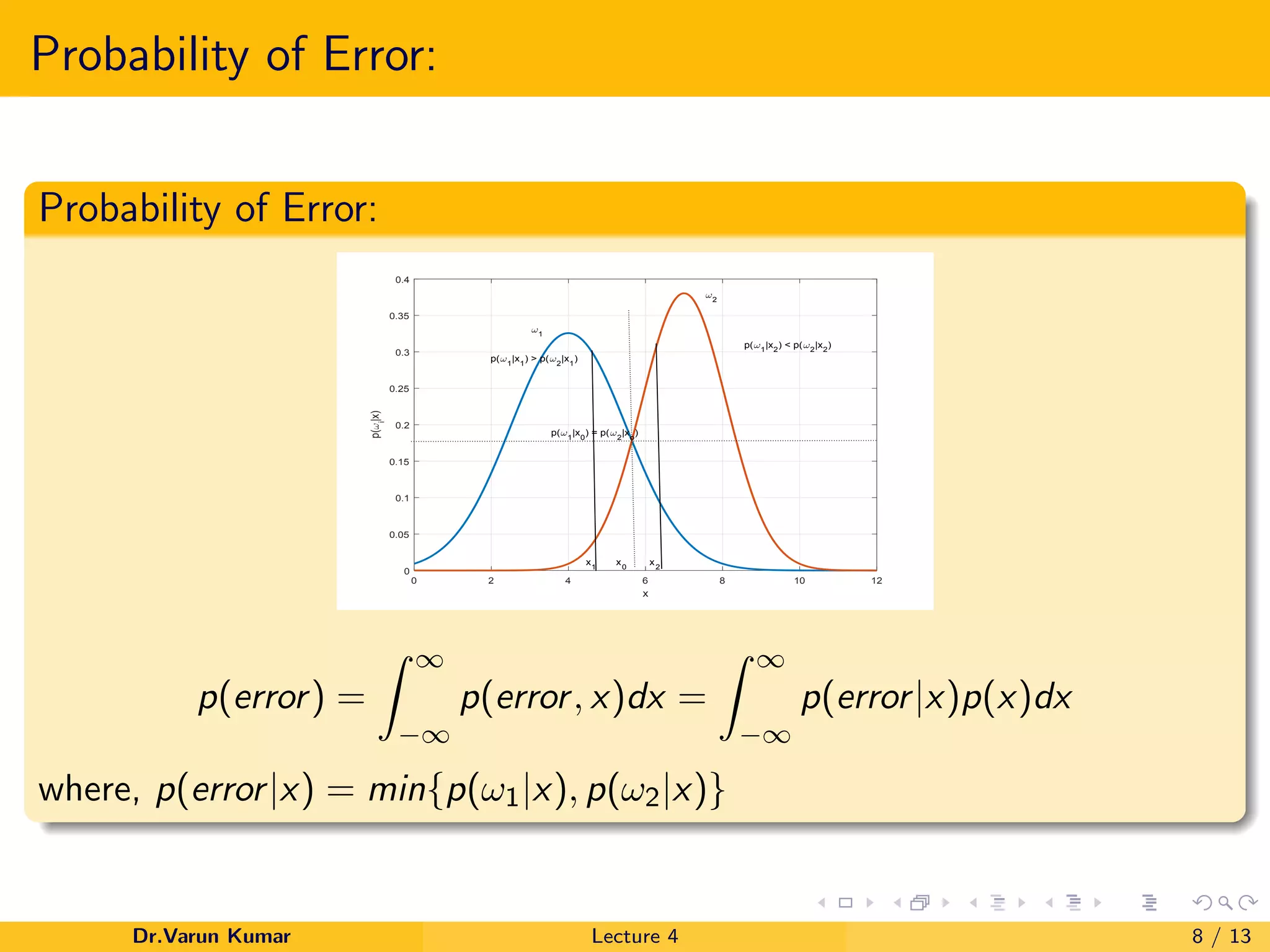
The document outlines Bayesian decision theory, emphasizing its framework for making rational decisions under uncertainty to minimize expected risk. It discusses concepts like a priori and a posteriori probabilities, joint probability, and the risk function in decision-making scenarios, particularly in artificial intelligence and machine learning. Additionally, it provides mathematical descriptions and examples to illustrate the probability of error and multiple class actions.