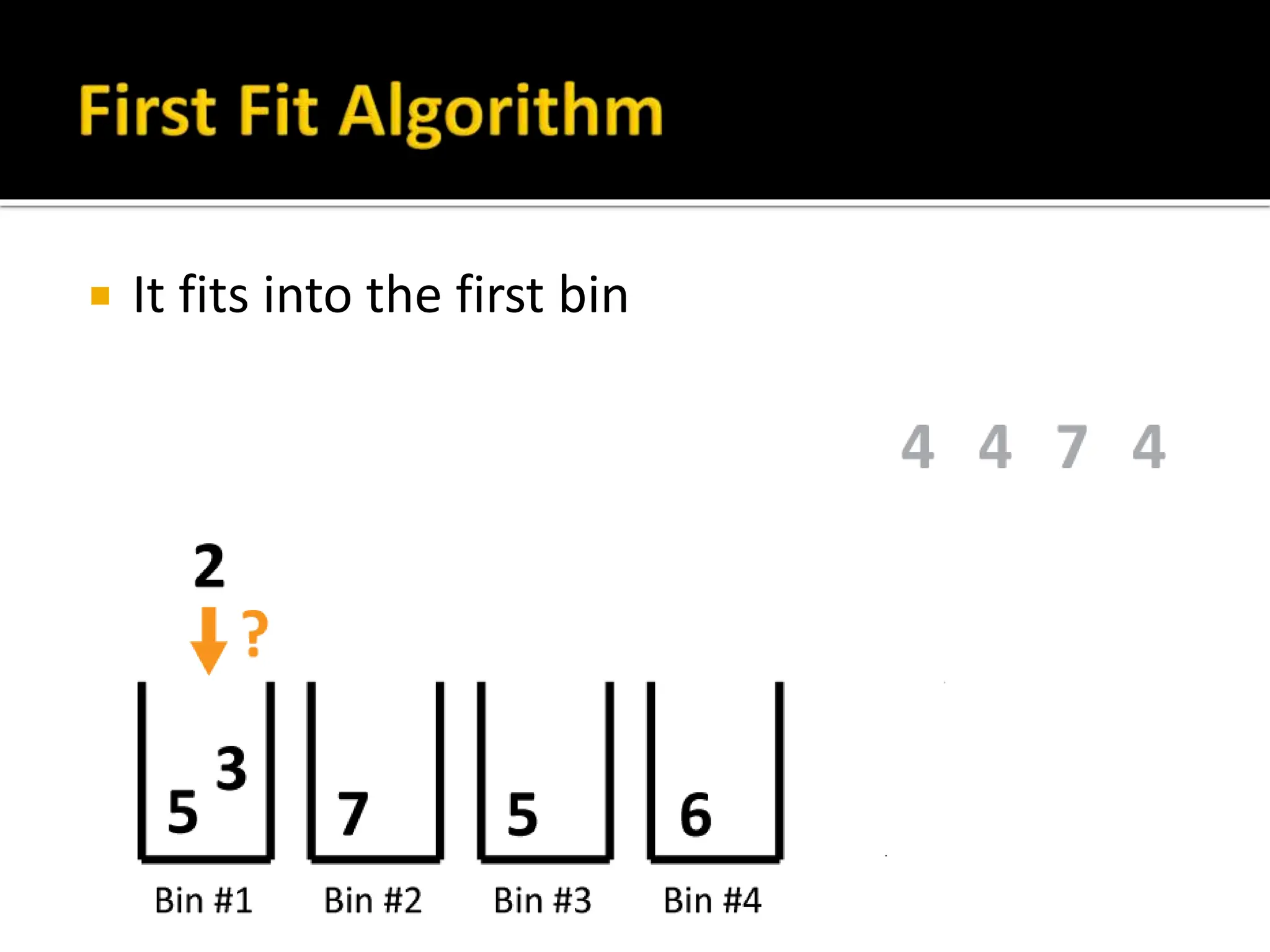
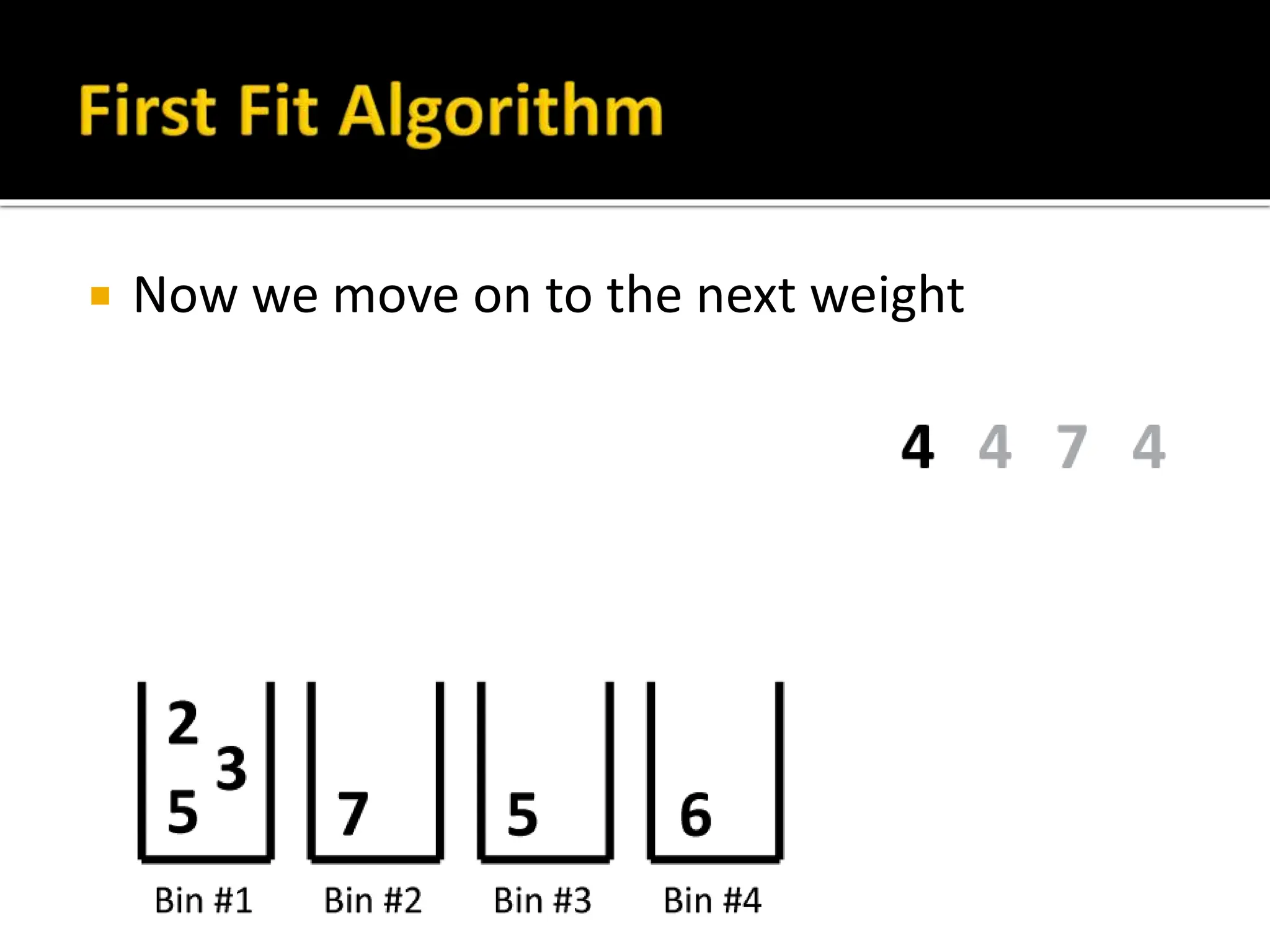
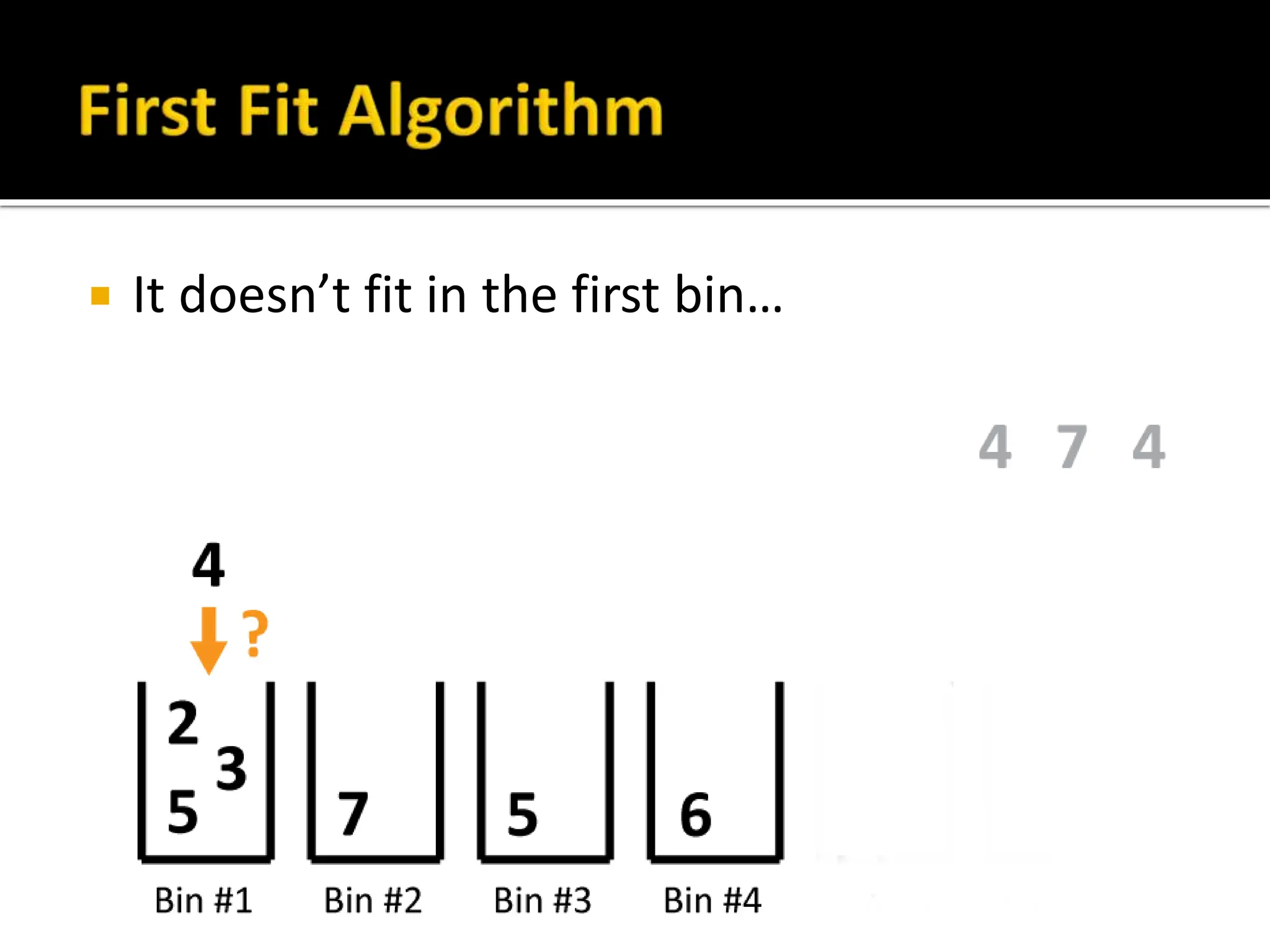
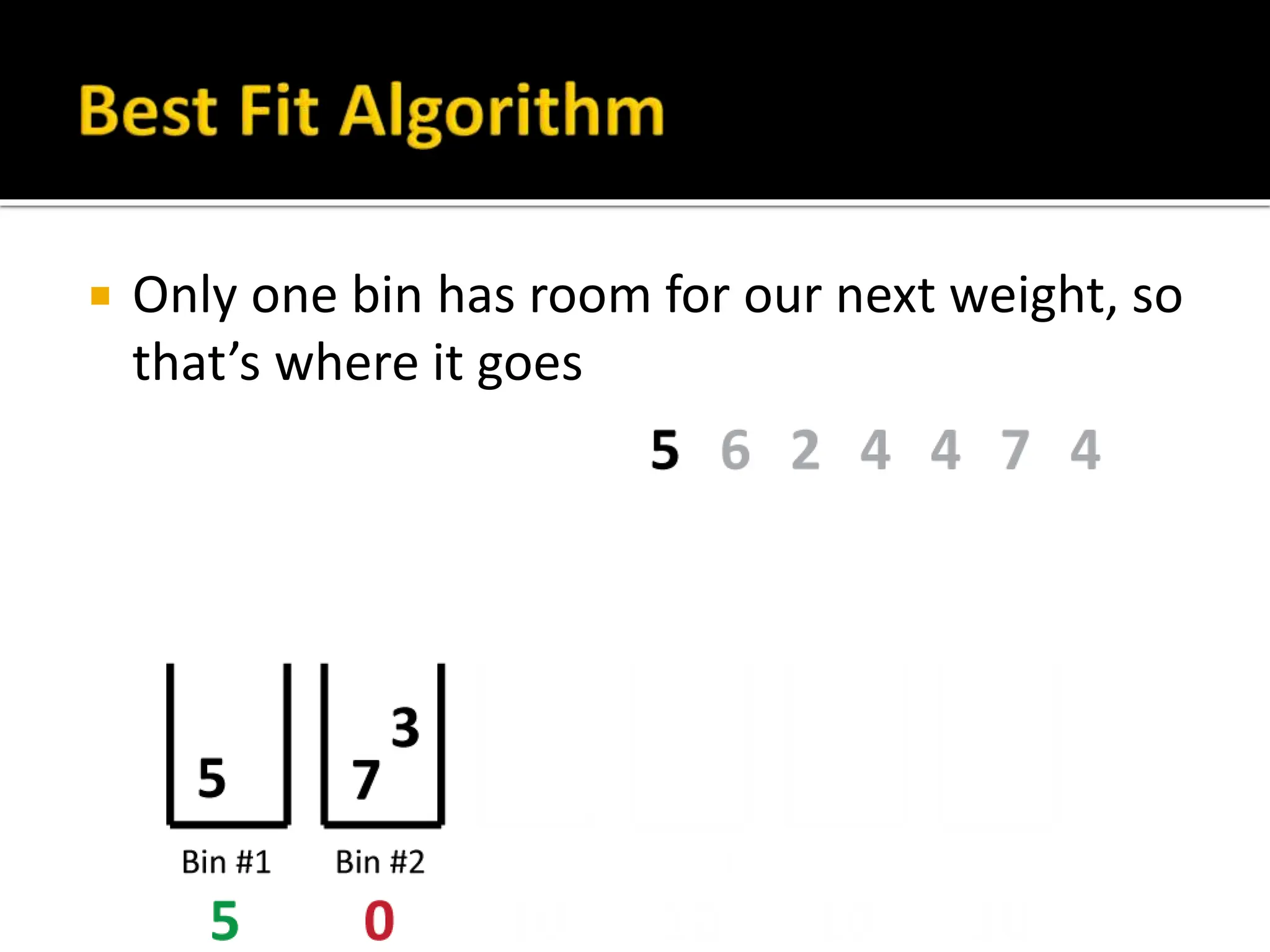
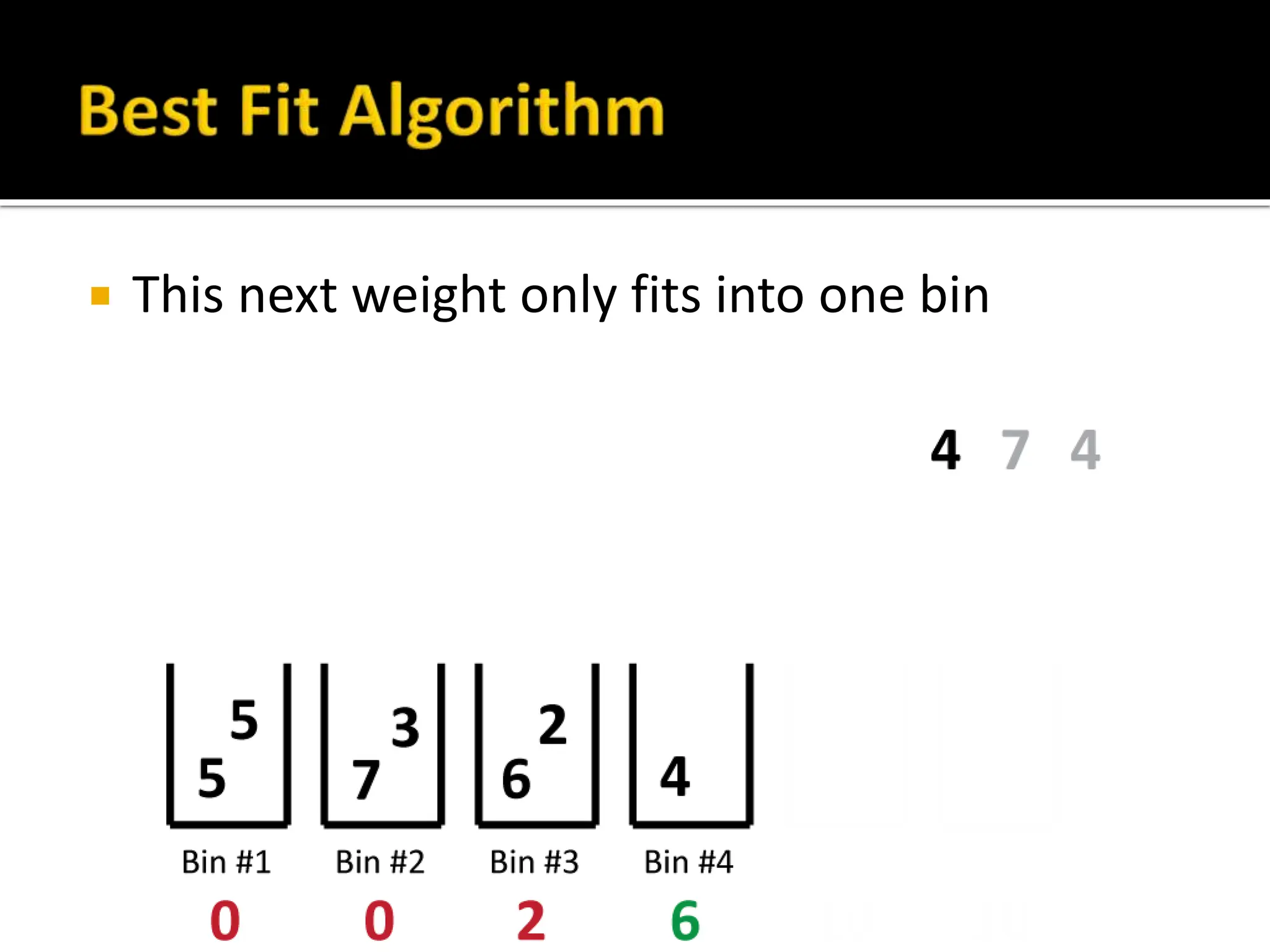
The document discusses bin packing and scheduling problems. Bin packing involves assigning weights (objects) to bins (containers) with the goal of using the fewest number of bins. Scheduling problems involve assigning tasks to processors (people, machines) to complete the tasks efficiently. Different algorithms like first fit, best fit, and longest processing time are presented for solving these types of problems. Examples are provided to demonstrate how to apply the algorithms to sample problems and their limitations.