Download to read offline
Uploaded byKalpana Mohan
Binary tree operations in data structures
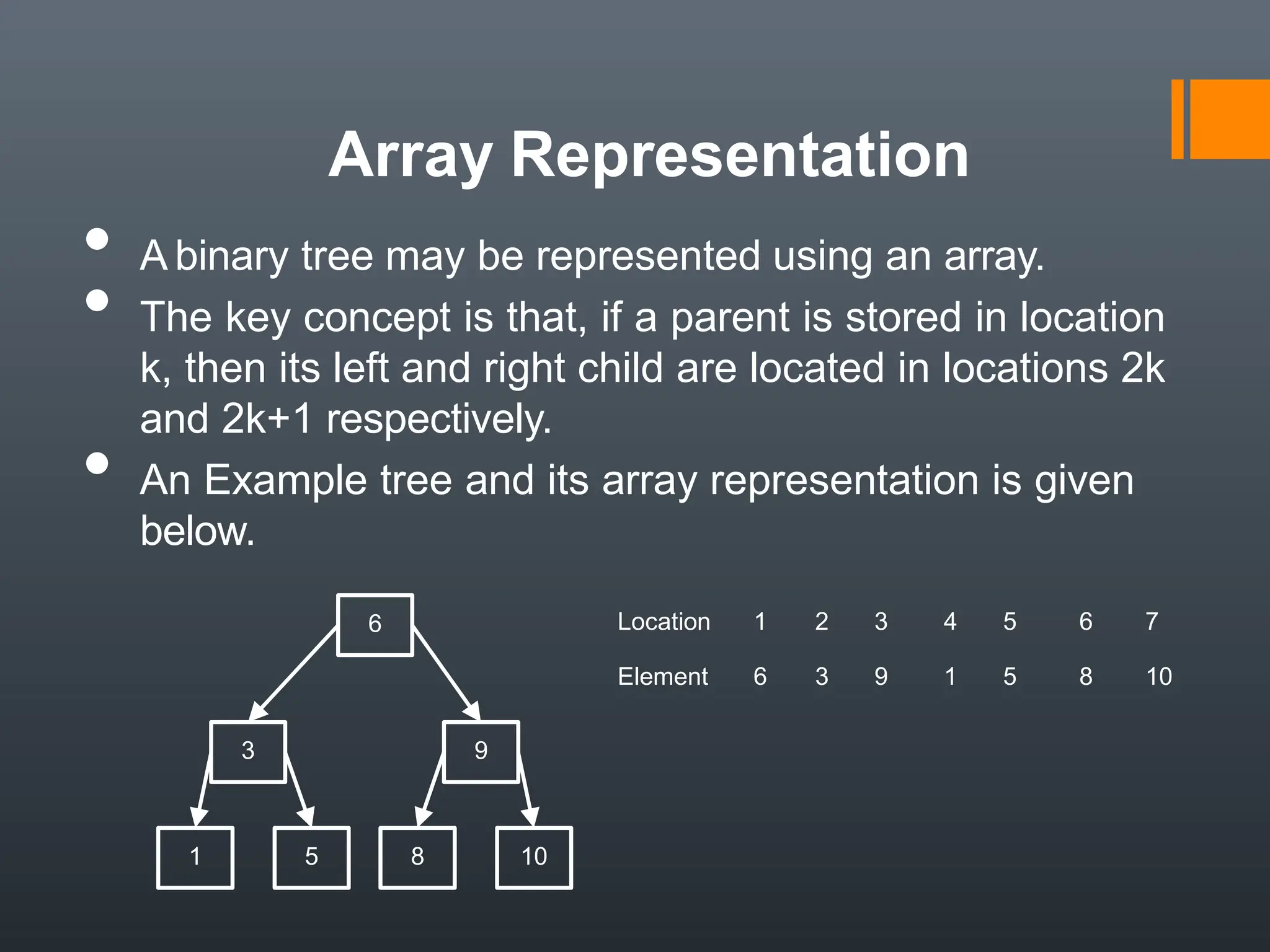
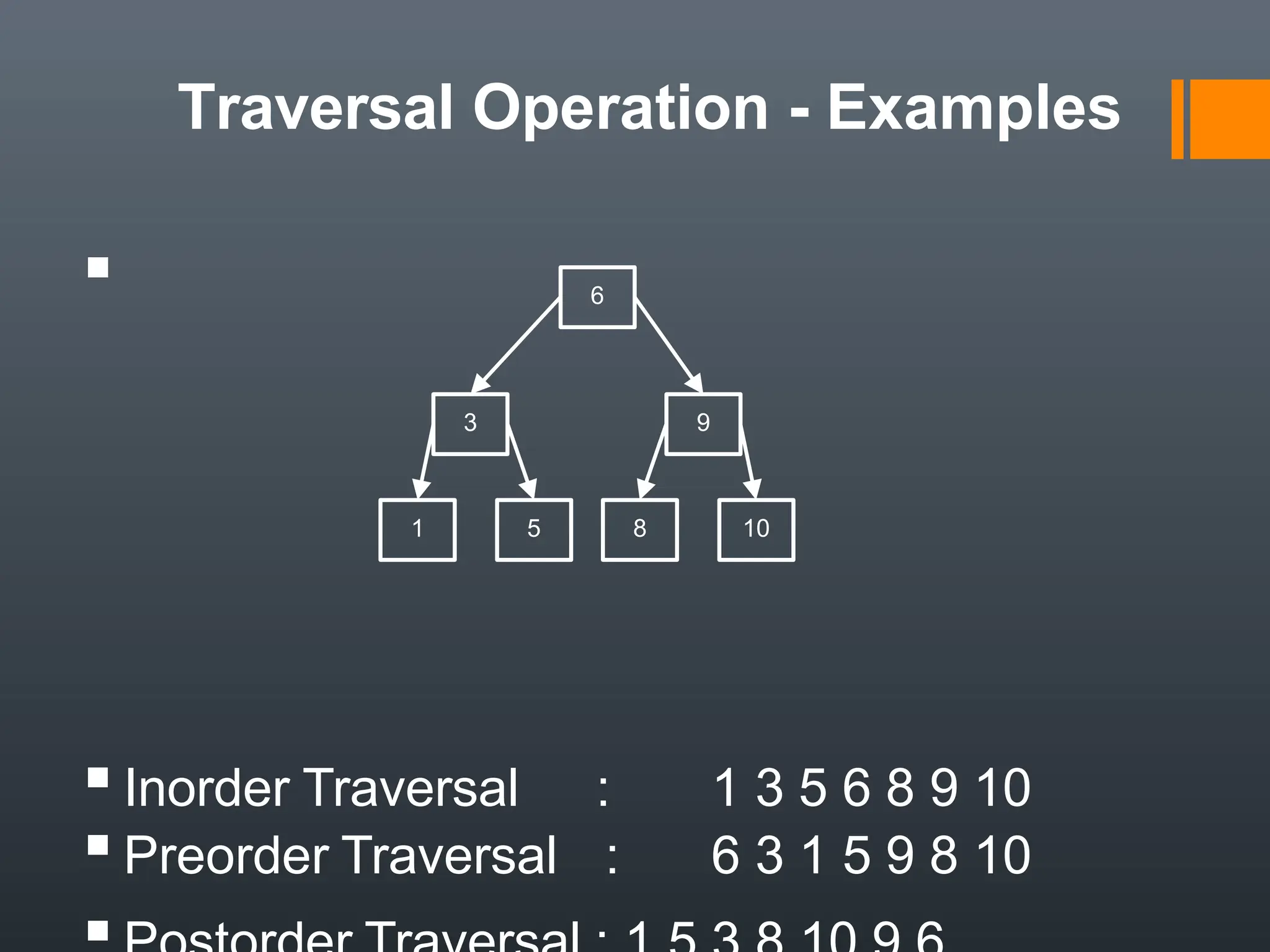
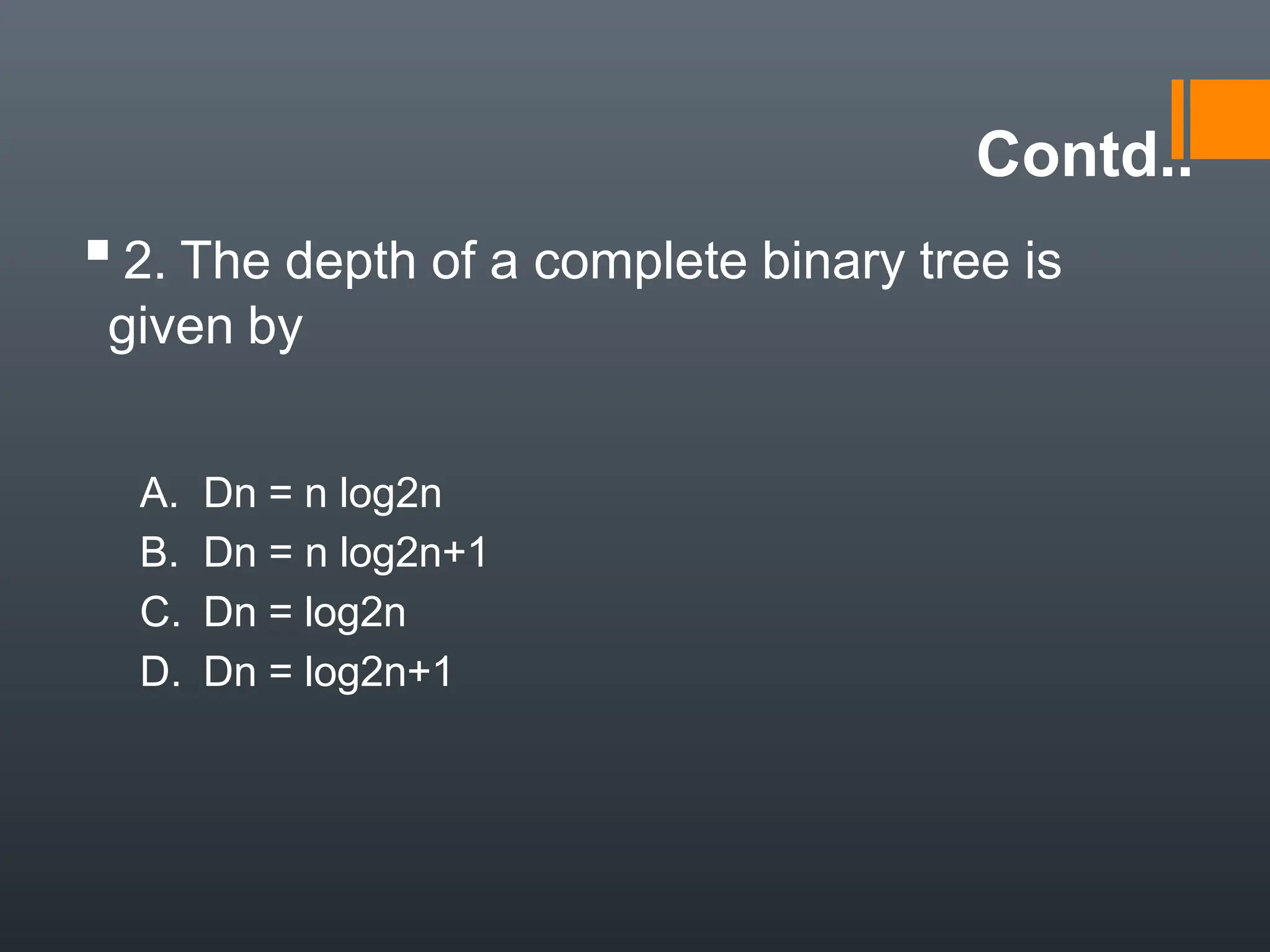
The document explains binary trees, defining a binary tree as a tree structure where each node has at most two children, and detailing the characteristics of complete and ordered binary trees. It discusses various operations such as insertion, deletion, searching, and different traversal methods, including pre-order, in-order, and post-order. Additionally, it outlines applications of binary trees in expression evaluation, data searching, and sorting, as well as different representations of binary trees.
More Related Content
![Data Structures - Lecture 9 [Stack & Queue using Linked List]](https://cdn.slidesharecdn.com/ss_thumbnails/lecture-9stackqueueusinglinkedlist-150219032411-conversion-gate02-thumbnail.jpg?width=600ounds&width=560&fit=bounds)
Similar to Binary tree operations in data structures
Binary tree operations in data structures
- 1.
- 2. Binary Tree andComplete Binary Tree ▪Binary Tree(BT) is a tree in which each node contains at most two child nodes(left child and right child). ▪A complete binary tree is a binary tree in which every node contains exactly two child nodes except the leaf nodes. Figure 1 shows a tree which is not a binary tree since node ‘3’ contains three child nodes. Figure 2 shows an example binary tree and Figure 3 shows a complete binary tree 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 Figure 1 Figure 2 Figure 3
- 3. Types of BinaryTree ▪Ordered Binary Tree: In an ordered binary tree, the left child node will always be less than its parent and right child node will greater than its parent. It is also known as Binary Search Tree. ▪Unordered Binary Tree: Unordered Binary tree does not follow any such ordering. ▪An example of ordered binary tree is given below. 6 3 9 8 10 5 1 In the rest of the slides we only focus on ordered binary tree since it has many applications including finding duplicates, data sorting and searching.
- 4. Operations on Binarytree Traversals •Traversal refers to visiting all the nodes of a binary tree exactly once in a systematic way. Insertion •Refers to inserting a new element into the tree Deletion •Refers to removing an element from the tree Searching •Search operation checks whether the given data is present in the tree or not.
- 5. Applications of Binarytree • Expression Evaluation (Expression tree) • Data Searching • Data sorting
- 6. Representation of BinaryTrees ▪Array Representation ▪Linked Representation ▪Threaded Representation
- 7. Array Representation • Abinary tree may be represented using an array. • The key concept is that, if a parent is stored in location k, then its left and right child are located in locations 2k and 2k+1 respectively. • An Example tree and its array representation is given below. 6 3 9 8 10 5 1 Location 1 2 3 4 5 6 7 Element 6 3 9 1 5 8 10
- 8. Traversal Operations ▪Pre-order Traversal 1.Process the root node 2. Perform preorder traversal of left subtree 3. perform preorder traversal of right subtree ▪In-order Traversal 1.Perform Inorder traversal of left subtree 2.Process the root node 3.Perform Inorder traversal of right subtree ▪Post-order Traversal 1.Perform Postorder traversal of left subtree 2.Perform Postorder traversal of right subtree 3.Process the root node
- 9. Traversal Operation -Examples ▪ ▪Inorder Traversal : 1 3 5 6 8 9 10 ▪Preorder Traversal : 6 3 1 5 9 8 10 6 3 9 8 10 5 1
- 10. NODE DECLARATION ▪typedef structtreeNode { int data; struct treeNode *left; struct treeNode *right; }treeNode;
- 11. INSERTION ROUTINE ▪treeNode *Insert(treeNode *node,int data) { if(node==NULL) { treeNode *temp; temp = (treeNode *)malloc(sizeof(treeNode)); temp -> data = data; temp -> left = temp -> right = NULL; return temp; } if(data >(node->data)) { node->right = Insert(node->right,data); } else if(data < (node->data)) { node->left = Insert(node->left,data); } /* Else there is nothing to do as the data is already in the tree. */ return node; }
- 12. DELETION ROUTINE ▪treeNode *Delete(treeNode *node, int data) { treeNode *temp; if(node==NULL) { printf("Element Not Found"); } else if(data < node->data) { node->left = Delete(node->left, data); } else if(data > node->data) { node->right = Delete(node->right, data); } else { /* Now We can delete this node and replace with either minimum element in the right sub tree or maximum element in the left subtree */
- 13. CONTD.. ▪ if(node->right &&node->left) { /* Here we will replace with minimum element in the right sub tree */ temp = FindMin(node->right); node -> data = temp->data; /* As we replaced it with some other node, we have to delete that node */ node -> right = Delete(node->right,temp->data); } else { /* If there is only one or zero children then we can directly remove it from the tree and connect its parent to its child */ temp = node; if(node->left == NULL) node = node->right; else if(node->right == NULL) node = node->left; free(temp); /* temp is longer required */ } } return node; }
- 14. FINDMIN ROUTINE ▪treeNode* FindMin(treeNode*node) { if(node==NULL) { /* There is no element in the tree */ return NULL; } if(node->left) /* Go to the left sub tree to find the min element */ return FindMin(node->left); else return node; }
- 15. How many squarescan you create in this figure by connecting any 4 dots (the corners of a square must lie upon a grid dot? TRIANGLES: How many triangles are located in the image below?
- 16. There are 11squares total; 5 small, 4 medium, and 2 large. 27 triangles. There are 16 one-cell triangles, 7 four-cell triangles, 3 nine-cell triangles, and 1 sixteen-cell triangle.
- 17.
- 19. ASSESSMENT ▪1. A binarytree whose every node has either zero or two children is called A. Complete binary tree B. Binary search tree C. Extended binary tree D. None of above
- 20. Contd.. ▪2. The depthof a complete binary tree is given by A. Dn = n log2n B. Dn = n log2n+1 C. Dn = log2n D. Dn = log2n+1
- 21. Contd.. ▪3.The post ordertraversal of a binary tree is DEBFCA. Find out the pre order traversal A. ABFCDE B. ADBFEC C. ABDECF D. ABDCEF
- 22. Contd.. ▪4.In a binarytree, certain null entries are replaced by special pointers which point to nodes higher in the tree for efficiency. These special pointers are called A. Leaf B. branch C. path D. thread
- 23. Contd.. ▪5. The in-ordertraversal of tree will yield a sorted listing of elements of tree in A. Binary trees B. Binary search trees C. Heaps D. None of above