CHAPTER 2 Simple Searching Algorithms.pptx

CHAPTER 2:
Simple Searching and
Sorting Algorithms

OUTLINE
Searching Algorithms
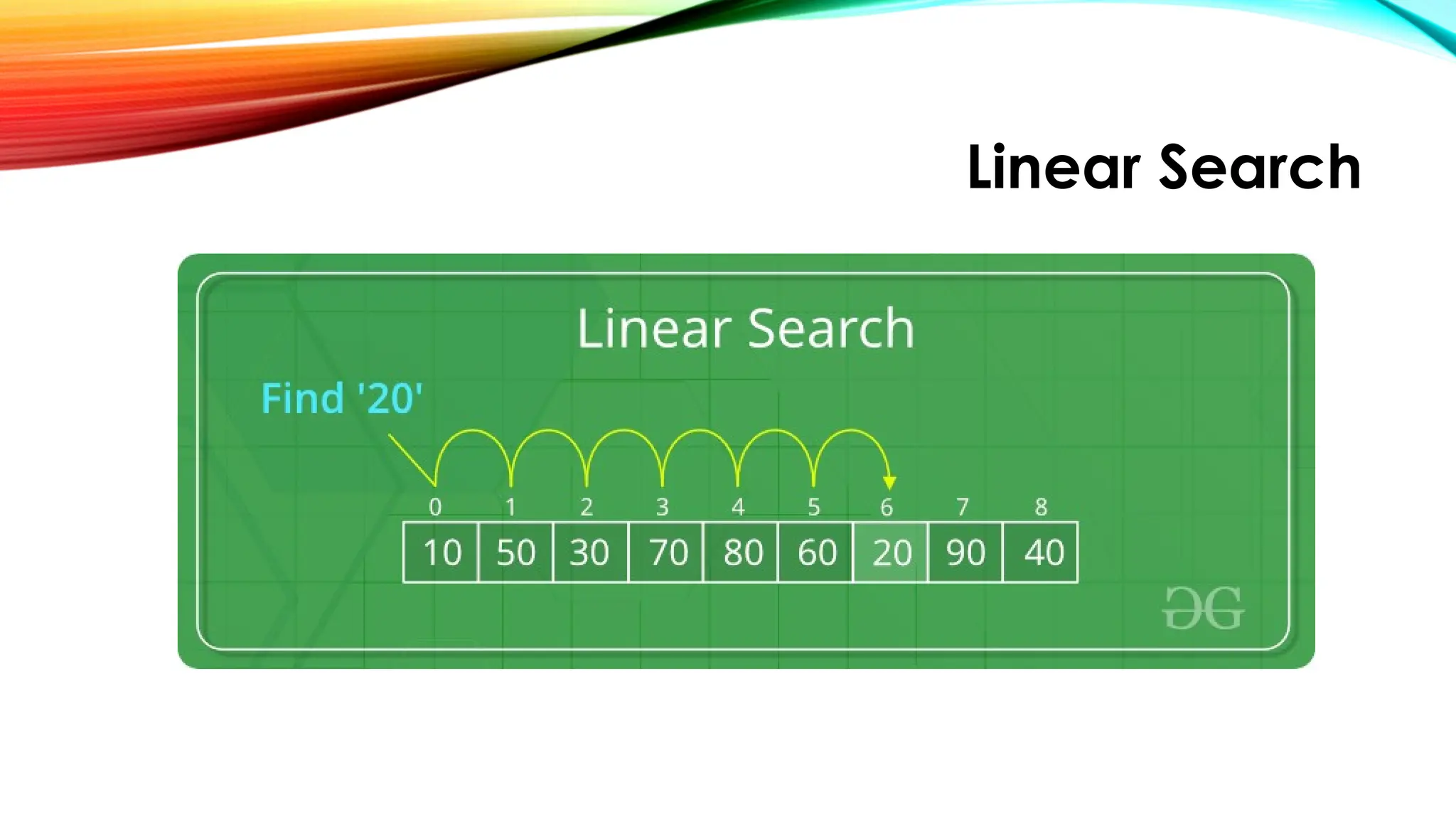
 Linear Search
 Binary Search
Sorting Algorithms
 Bubble Sort
 Insertion Sort
 Selection Sort

Linear Search
• What is Searching Algorithm?
• Searching Algorithms are designed to check for an
element or retrieve an element from any data structure
where it is stored.
• Linear Search: Know as Sequential Search: In this, the list or
array is traversed sequentially and every element is
checked.

Linear Search
• A linear search is the simplest approach employed to
search for an element in a given data set.
• It examines each element until it finds a match, starting at
the beginning of the data set, until the end.

Linear Search
• Linear Search starts at one end and goes through each
element of a list until the desired element is found,
otherwise the search continues till the end of the data set.
• It should also reports if the target is nor found in the list.

Linear Search
How Does Linear Search Algorithm Work?
Every element is considered as a potential match for the
key and checked for the matching.
If any element is found equal to the key, the search is
successful and the index of that element is returned.
If no element is found equal to the key, the search yields
“No match found”.
For example: Consider the array arr[] = {10, 50, 30, 70,
80, 20, 90, 40} and key = 30.

Linear Search
Step 1: Start from the first element (index 0) and
compare key with each element (arr[i]).
Comparing key with first element arr[0]. SInce not equal,
the iterator moves to the next element as a potential
match.

Linear Search
Comparing key with next element arr[1]. Since not equal,
the iterator moves to the next element as a potential
match.

Linear Search
Step 2: Now when comparing arr[2] with key, the value
matches. So the Linear Search Algorithm will yield a
successful message and return the index of the element
where key is found (Here 2).

Linear Search
procedure linear_search (list, value)
for each item in the list
if match item == value
return the item's location
end if
end for
end procedure

Linear Search
Complexity Analysis of Linear Search:
• Time Complexity:
• Best Case: In the best case, the key might be present at the first index. So
the best case complexity is O(1)
• Worst Case: In the worst case, the key might be present at the last index
i.e., opposite to the end from which the search has started in the list. So the
worst-case complexity is O(N) where N is the size of the list.
• Average Case: O(N).
• Auxiliary Space: O(1) as except for the variable to iterate through the list,
no other variable is used.

Linear Search
Advantages of Linear Search:
• Linear search can be used irrespective of whether the array is sorted or not.
• It can be used on arrays of any data type.
• Does not require any additional memory.
• It is a well-suited algorithm for small datasets.
Drawbacks of Linear Search:
• Not suitable for large arrays.

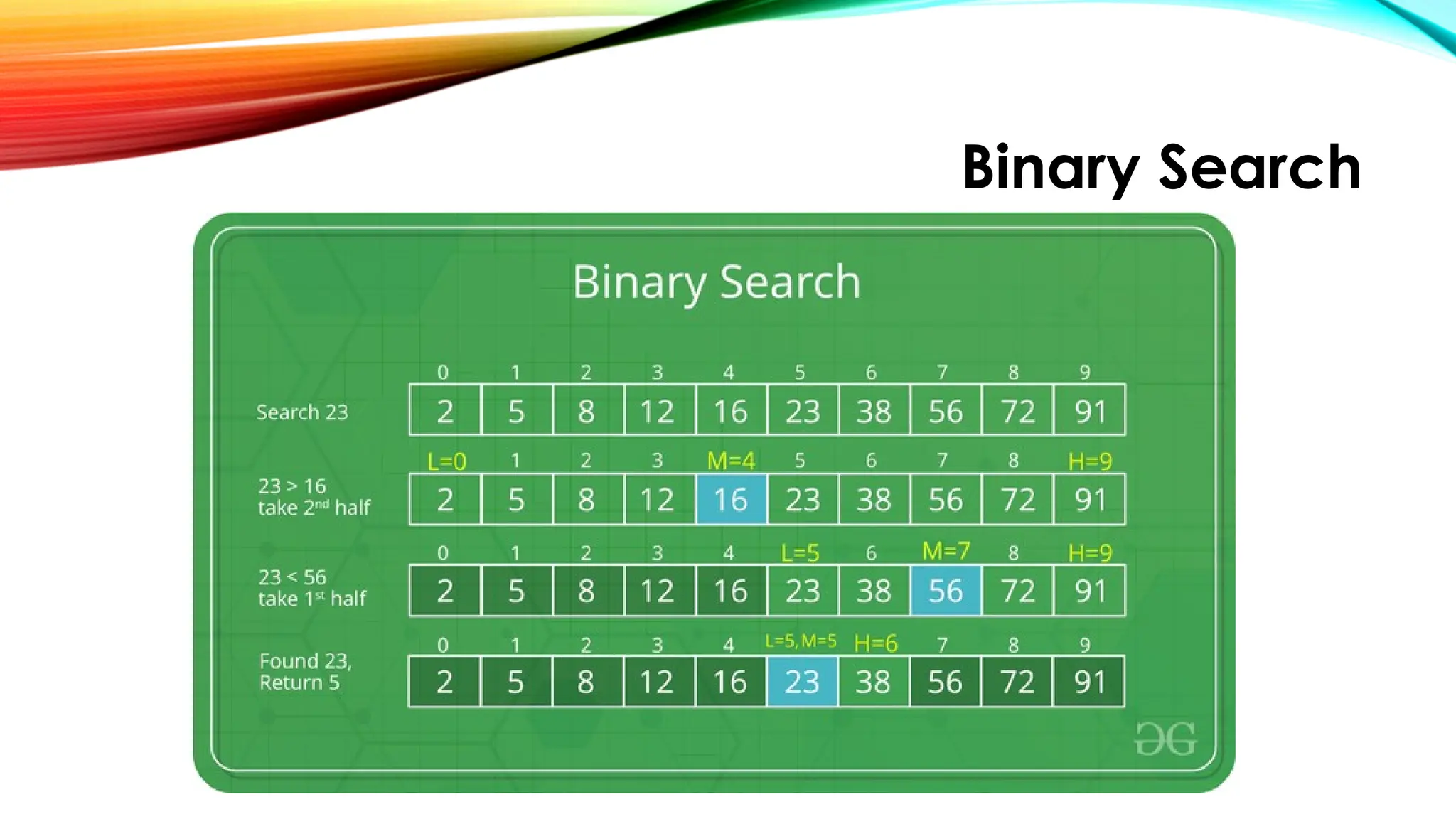
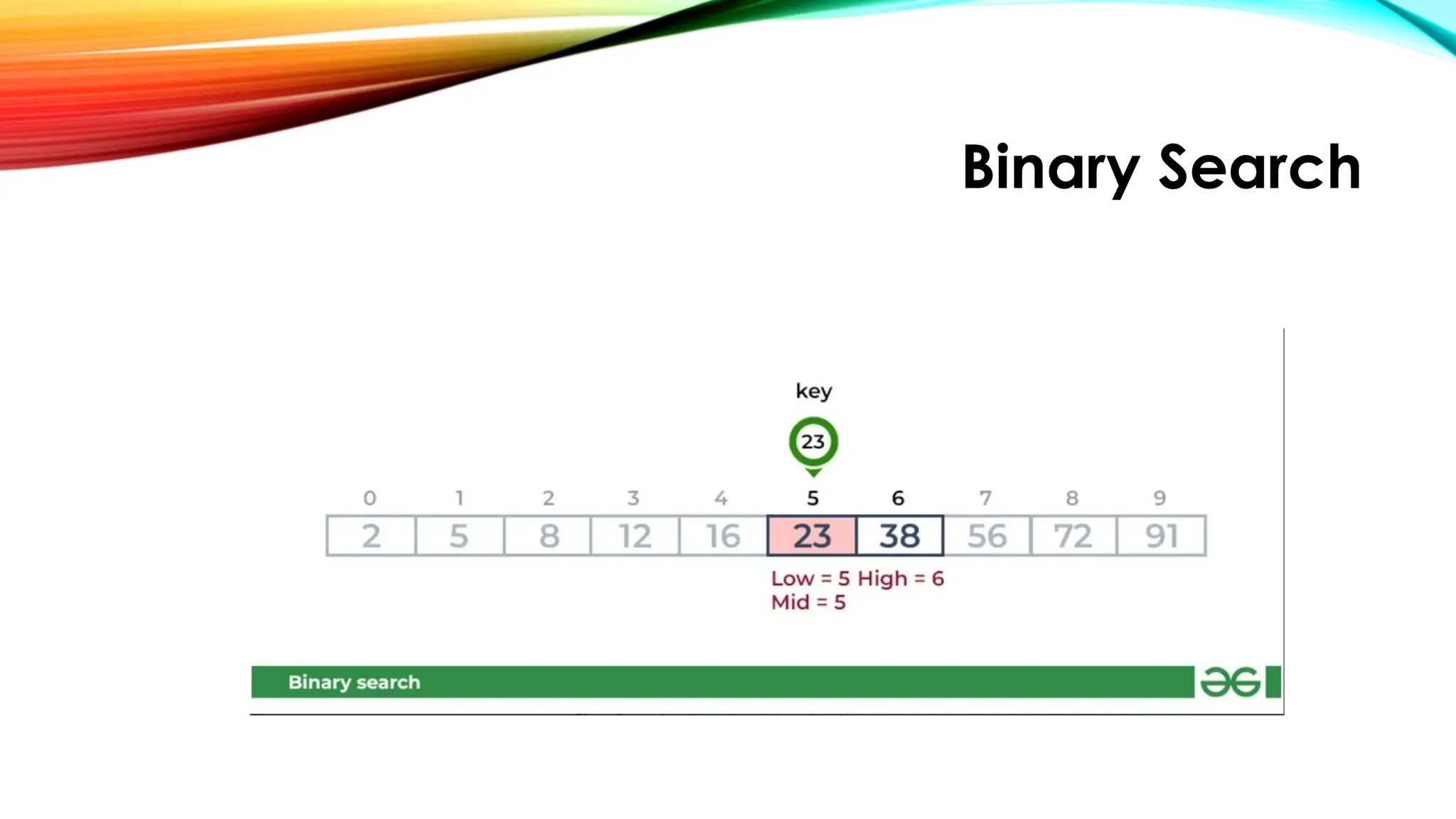
Binary Search
Binary Search: also know as Interval Search: These algorithms
are specifically designed for searching in sorted data-
structures.
These type of searching algorithms are much more efficient
than Linear Search.

Binary Search
 It works by repeatedly dividing the search interval in half. The idea
of binary search is to use the information that the array sorted and
reduce the time complexity to O(log N).
 Pre Conditions:
• The data structure must be sorted.
 Divide the search space half by finding the middle index , “mid”.

Binary Search
Finding the middle index “mid” in Binary Search Algorithm

Binary Search
• Compare the middle element of the search space with the key.
• If the key is found at middle element, the process is terminated.
• If the key is not found at middle element, choose which half will be
used as the next search space.
• If the key is smaller than the middle element, then the left side is
used for next search.
• If the key is larger than the middle element, then the right side is
used for next search.
• This process is continued until the key is found or the total search
space is exhausted.

Binary Search
Demonstration:
• Consider an array arr[] = {2, 5, 8, 12, 16, 23, 38, 56, 72, 91},
and the target = 23.
• First Step: Calculate the mid and compare the mid
element with the key. If the key is less than mid element,
move to left and if it is greater than the mid then move
search space to the right.
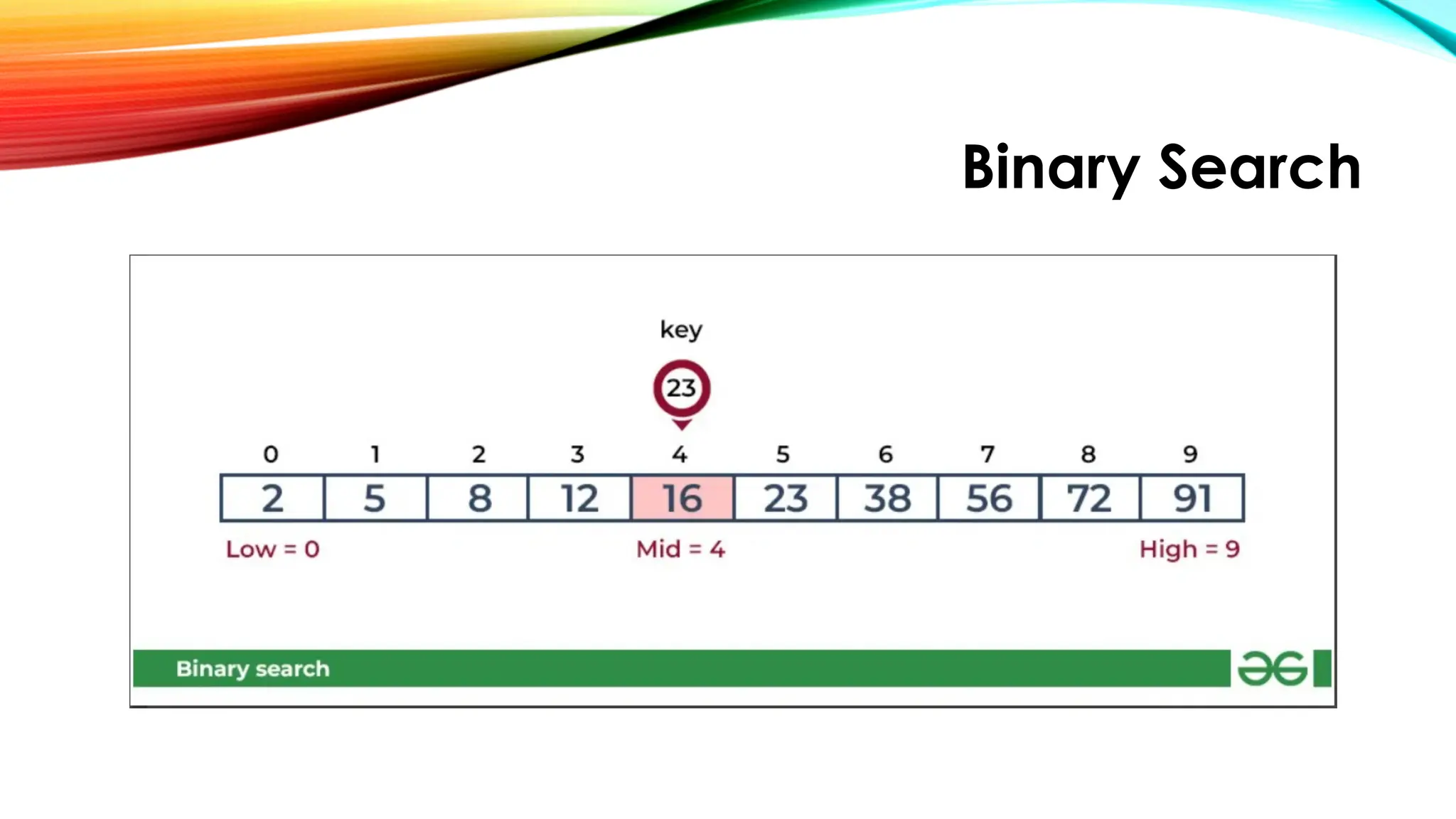
• Key (i.e., 23) is greater than current mid element (i.e., 16).
The search space moves to the right.

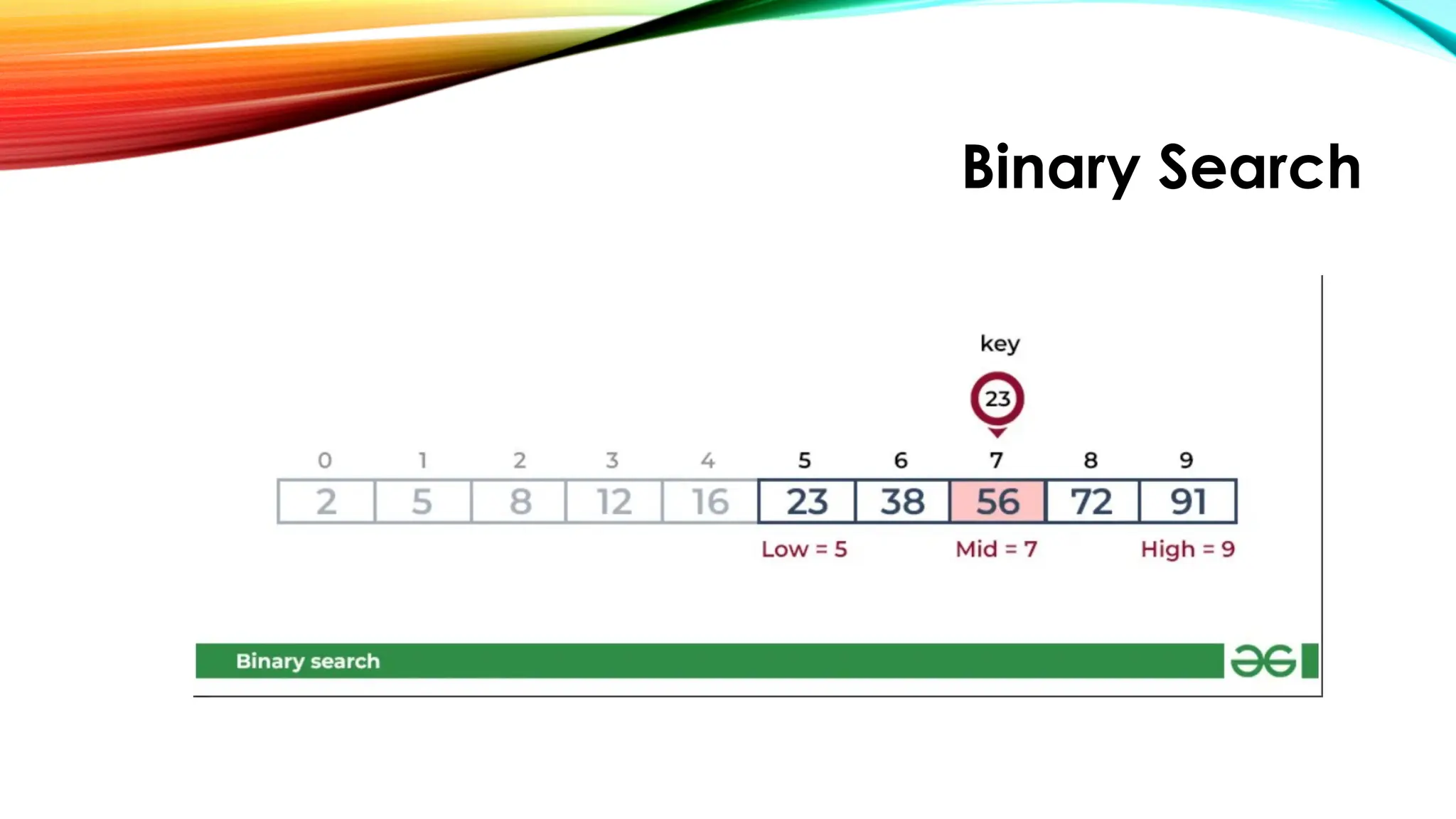
Binary Search
function binary_search(list, target):
left = 0
right = length(list) - 1
while left <= right:
mid = (left + right) // 2
if list[mid] == target:
return mid
elif list[mid] < target:
left = mid + 1
else:
right = mid - 1
return -1

Binary Search
How to Implement Binary Search?
• The Binary Search Algorithm can be implemented in the
following two ways
• Iterative Binary Search Algorithm
• Recursive Binary Search Algorithm
Time Complexity: O(log N)
Auxiliary Space: O(1)

CHAPTER 2 Simple Searching Algorithms.pptx

More Related Content

Similar to CHAPTER 2 Simple Searching Algorithms.pptx

More from shambelworku8

Recently uploaded

CHAPTER 2 Simple Searching Algorithms.pptx

Editor's Notes