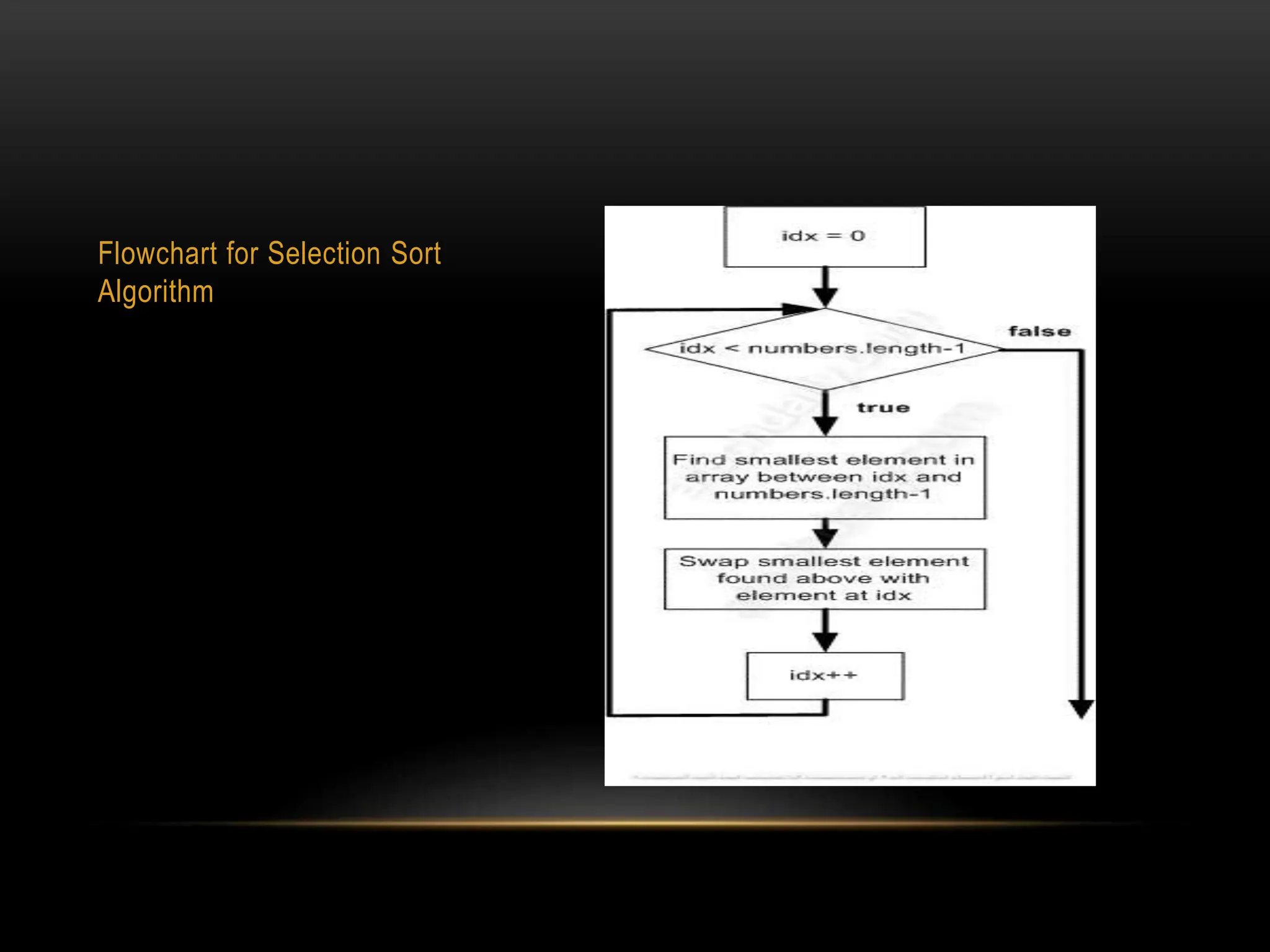
Selection sort is a simple sorting algorithm that works by repeatedly finding the minimum element in the unsorted portion of the array and swapping it into the sorted position. It divides the array into a sorted and unsorted portion, initially with the entire array unsorted. It iterates through the unsorted portion, finds the minimum element, and swaps it into the sorted portion. This continues until the entire array is sorted. The algorithm has an average and worst-case time complexity of O(n2) due to its use of nested loops. A flowchart demonstrates the step-by-step process of selection sort on an example array.