Computer Graphics - Hidden Line Removal Algorithm

SUBMITTED BY:
JYOTIRAMAN DE
M TECH (CAD/CAM)

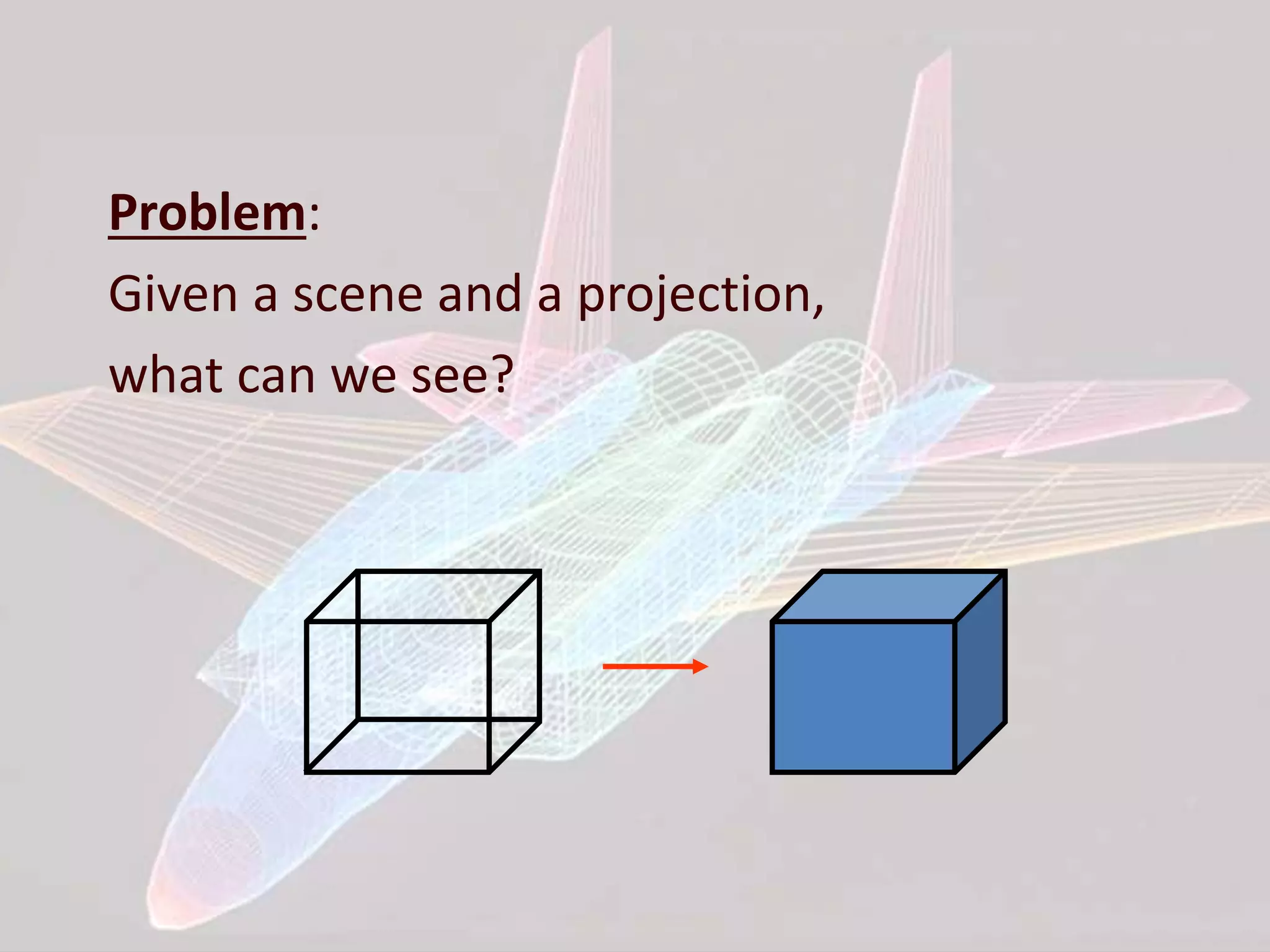
Problem:
Given a scene and a projection,
what can we see?

Two main types of algorithms:
Object space: Determine which part of the object are
visible. Also called as World Coordinates
Image space: Determine per pixel which point of an
object is visible. Also called as Screen Coordinates
Object space Image space

Two main Hidden Surface Removal Algorithm
Techniques:
Object space: Hidden Surface Removal for all
objects
Image space:
Objects: 3 D Clipping
Transformed to Screen Coordinates
Hidden Surface Removal

ALGORITHMS WE ARE GOING TO DISCUSS:
• Z-buffer method
• Scan-line method
• Spanning scan-line method
• Floating horizon method
• Discrete data method

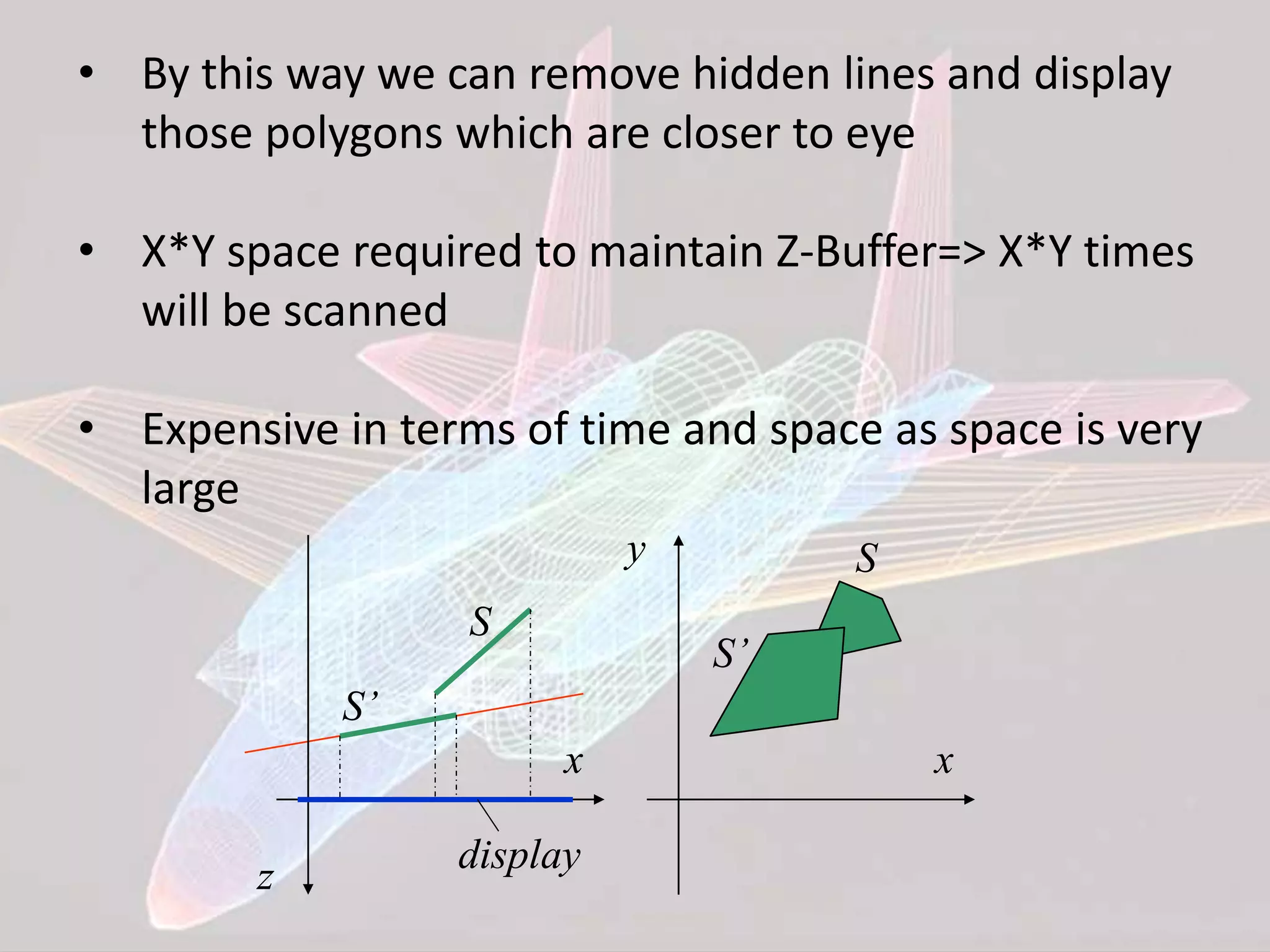
Z-BUFFER ALGORITHM:
• Its an extension of Frame Buffer
• Display is always stored on Frame Buffer
• Frame Buffer stores information of each and every
pixel on the screen
• Bits (0, 1) decide that the pixel will be ON or OFF
• Z- Buffer apart from Frame buffer stores the depth
of pixel
• After analyzing the data of the overlapping
polygons, pixel closer to the eye will be updated
• Resolution of X,Y => Array[X,Y]

Given set of polygon in image space
Z-Buffer Algorithm:
1. Set the frame buffer & Z-Buffer to a background
value
(Z-BUFFER=Zmin) where, Zmin is value
To display polygon decide=>color, intensity and depth
2. Scan convert each polygon
i.e, for each pixel, find depth at that point
If Z(X,Y)>Z-BUFFER(X,Y)
Update Z-BUFFER(X,Y)=Z(X,Y)
& FRAME BUFFER
This process will repeat for each pixel

• By this way we can remove hidden lines and display
those polygons which are closer to eye
• X*Y space required to maintain Z-Buffer=> X*Y times
will be scanned
• Expensive in terms of time and space as space is very
large
x
z display
S
S’
x
y S
S’

Pseudocode for the z-buffer algorithm
void zBuffer(void)
{
int x,y;
for(y=0;y<YMAX;y++) { /*Clear frame buffer and z-buffer*/
for(x=0;x<XMAX;x++) {
WritePixel(x,y,BACKGROUND_VALUE);
WriteZ(x,y,0);
}
}
for(each polygon) { /*Draw Polygons*/
for(each pixel in polygons projection) {
double pz=polygons z-value at pixel coords(x,y);
if(pz>=ReadZ(x,y)) { /*New point is not farther*/
WriteZ(x,y,pz);
WritePixel(x,y,polygons color at pixel coords(x,y));
}
}
}
}

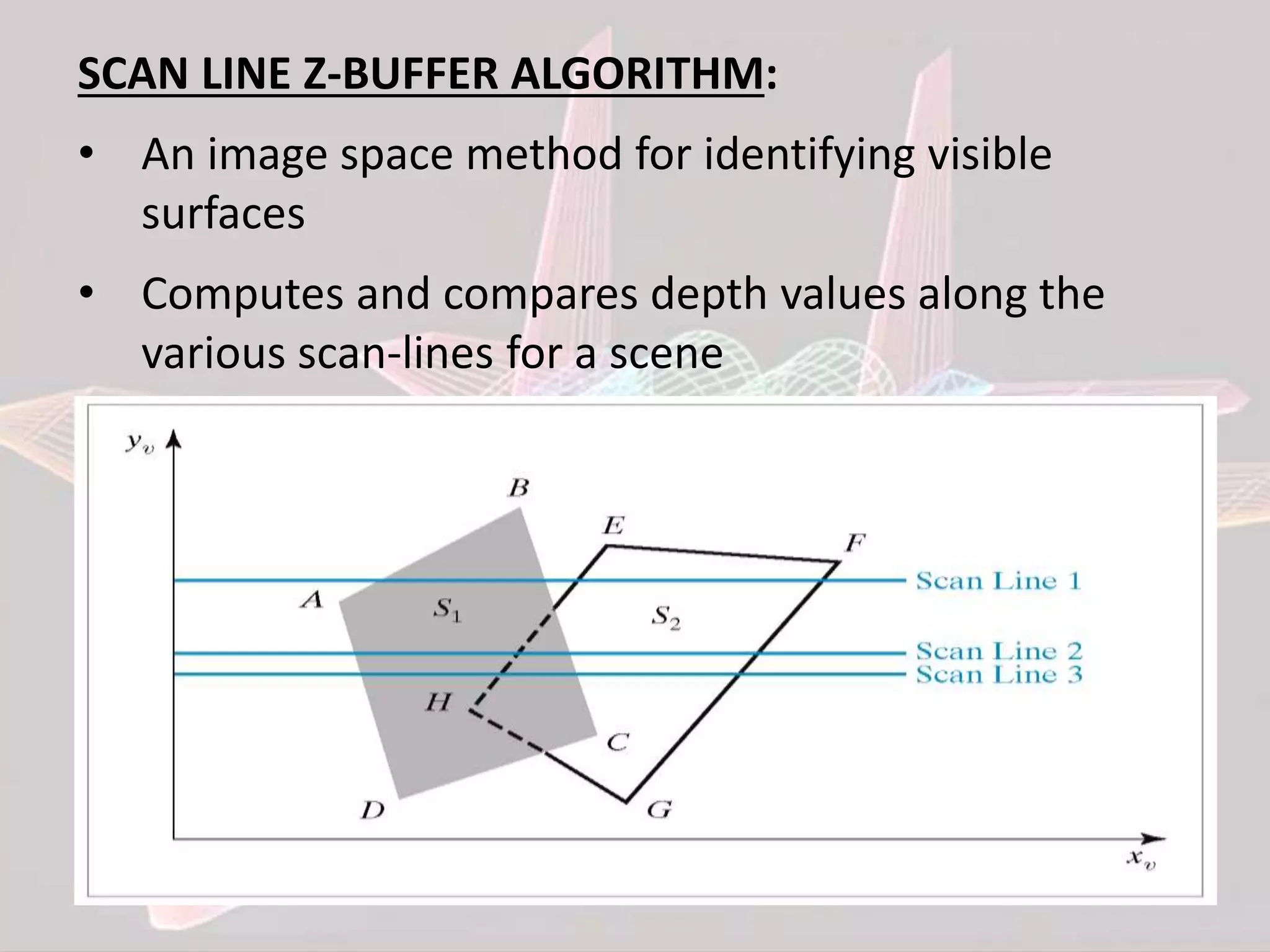
SCAN LINE Z-BUFFER ALGORITHM:
• An image space method for identifying visible
surfaces
• Computes and compares depth values along the
various scan-lines for a scene

• Scanning takes place row by row
• To facilitate the search for surfaces crossing a given
scan-line an active list of edges is formed for each
scan-line as it is processed
• The active list stores only those edges that cross the
scan-line in order of increasing x
• Pixel positions across each scan-line are processed
from left to right
• We only need to perform depth calculations
• In Scan Line, Z-Buffer(X) whereas earlier it was X*Y

Use Z-Buffer for only 1 scan line / 1 row of pixel
• During scan conversion in the Active Edge List(AEL)=>
Calculate Z(X,Y)
i.e, -Pixel info between 1 & 2 active edges will only
be stored
-Next pixel will be stored as z=z1+∆z
-∆z will be constant but can change anywhere in
case of slope
• If Z(X,Y)>Z BUFFER(X) => Update
• If 2 polygons are present-along with Active Edge List,
Active Polygon List will also be included
• Active Polygon List=> List of polygons intersecting a
scan line

Pseudocode for the general scan line algorithm
Add surfaces to surface table;
Initialize active-surface table;
for(each scan line)
{
update active-surface table;
for(each pixel on scan line)
{
determine surfaces in active-surface table that project to pixel;
find closest such surface;
determine closest surface’s shade at pixel;
}
}

SPANNING SCAN LINE Z-BUFFER ALGORITHM:
• Z-Buffer is not applicable
• Scan conversion is not done
• Speed increases

1 2 3 4 5 6
Each span at
most one
polygon shall be
displayed
• For each polygon determine the highest scan line
intersected by it
• Place the polygon in the Y-Bucket of that scan line
[YB]
• For each scan line
-Examine YB for any new polygon
-Add new polygon to APL
-Update AEL
-Divide into spans
-In each span decide which polygon shall be displayed
-Increment Y, update AEL & APL

FLOATING HORIZON ALGORITHM:
• Used for displaying surface
• Take each plane & intersection
z=constant plane and get a curve
from F(x,y)=0 f(x,y,z)=0
Array HORIZONTAL[X]=Ymax
Curve in each plane=>f(x,y)=0
y=f(x,y)
z=constant curves
Family of curves

1. Sort all curves as per z-coordinates
2. Start by z=constant curve closest to eye
- If at any x-value Y=f(x,y)
Y<HORIZON(X)-curve is hidden
- If Y>HORIZON(X)-curve is visible &
update HORIZON(X)=Y
- If Y<HORIZON-L(X) : curve is visible &
update HORIZON L(X)=Y
- If Y>HORIZON-U(X) : HORIZON U(X)=Y

• Above Algorithm are applied on surfaces which is in
the form of mathematical equation
• If this curve is not a mathematical equation like this
but it is a set of discrete data points then this
algorithm might not be directly useful

• Maintain HORIZON[X] at each side
• While displaying next curve, it will be compared to 2
points i.e, Y(Xi) & Y(Xi+1)
• If both points are visible, then the complete curve is
visible
• Algorithm will be complex as the curve is in discrete
data form
Y(Xi) Y(Xi+1) Result
V V Curve is visible
V I Xi to Intersection -> Visible
Intersection to Xi+1 -> NOT Visible
I V Xi to Intersection -> NOT Visible
Intersection to Xi+1 -> Visible
I I NOT Visible

SUMMARY
• We need to make sure that we only draw
visible surfaces when rendering scenes
• There are a number of techniques for doing
this such as
– Z-buffer method
– Scan-line method
– Spanning scan-line method
– Floating horizon method
– Discrete data method

REFERENCES
• NPTEL Video Lectures: CAD by Dr. Anoop Chawla, Dept. of
Mechanical Engineering, Indian Institute of Technology, Delhi,
Lecture No. # 12,13,14
• Ibrahim Zeid, “CAD/CAM” TMH
• Hoschek J, Dieter L, “Fundamentals of Computer Aided
Geometric Design ”, A K Peters, 1997
• Rogers D F I and Adams J A, “Mathematical Elements for
Computer Graphics”, McGraw-Hill, 1996
• J.H. Hughes, J.D.F., A.V.M., S.K.F., “Computer Graphics
Principles And Practice”, Pearson Education Asia,2001

Computer Graphics - Hidden Line Removal Algorithm

Computer Graphics - Hidden Line Removal Algorithm

More Related Content

What's hot

Viewers also liked

Similar to Computer Graphics - Hidden Line Removal Algorithm

Recently uploaded

In this document

Computer Graphics - Hidden Line Removal Algorithm