Computing on Encrypted Data

COMPUTING ON ENCRYPTED DATA
Shai Halevi, IBM Research
January 5, 2012

Computing on Encrypted Data

I want to delegate processing of my data,
without giving away access to it.

• Wouldn’t it be nice to be able to…
– Encrypt my data before sending to the cloud
– While still allowing the cloud to
search/sort/edit/… this data on my behalf
– Keeping the data in the cloud in encrypted form
• Without needing to ship it back and forth to be
decrypted

• Wouldn’t it be nice to be able to…
– Encrypt my queries to the cloud
– While still allowing the cloud to process them
– Cloud returns encrypted answers
• that I can decrypt

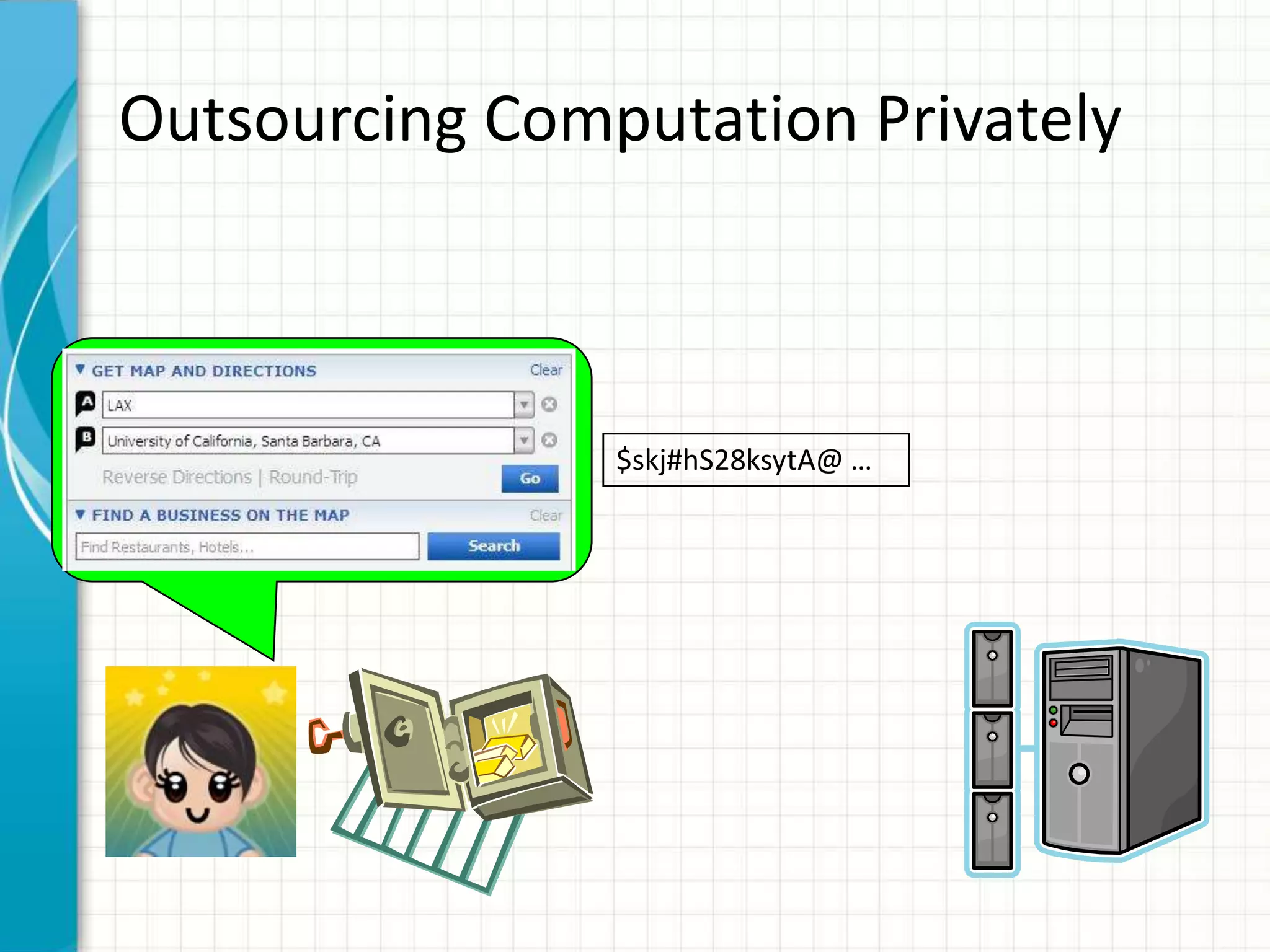
Outsourcing Computation Privately

“I want to delegate the computation to the cloud,
“I wantthe cloud the computation to the cloud”
but to delegate shouldn’t see my input”

Enc(x) f

Enc[f(x)]
Client Server/Cloud
(Input: x) (Function: f)


$skj#hS28ksytA@ …

$kjh9*mslt@na0
&maXxjq02bflx
m^00a2nm5,A4.
pE.abxp3m58bsa
(3saM%w,snanba
nq~mD=3akm2,A
Z,ltnhde83|3mz{n
dewiunb4]gnbTa*
kjew^bwJ^mdns0

Privacy Homomorphisms
• Rivest-Adelman-Dertouzos 1978
Plaintext space P Ciphertext space C
x1 x2 ci  Enc(xi) c1 c2

y  Dec(d)
y d

Example: RSA_encrypt(e,N)(x) = xe mod N
• x1e x x2e = (x1 x x2) e mod N
“Somewhat Homomorphic”: can compute some
functions on encrypted data, but not all

“Fully Homomorphic” Encryption
• Encryption for which we can compute arbitrary
functions on the encrypted data
Enc(x) Eval f

Enc(f(x))

• Another example: private information retrieval
i Enc(i) A[1 … n]
Enc(A[i])

Step 1: Boolean Circuit for f
• Every function can be constructed from
Boolean AND, OR, NOT
– Think of building it from hardware gates
• For any two bits b1, b2 (both 0/1 values)
– NOT b1 = 1 – b1
– b1 AND b2 = b1 b2
– b1 OR b2 = b1+b2– b1 b2
• If we can do +, – , x, we can do everything

Step 2: Encryption Supporting ,
• Open Problem for over 30 years
• Gentry 2009: first plausible scheme
– Security relies on hard problems in integer lattices
• Several other schemes in last two years

Fully homomorphic encryption
is possible

Performance
• A little slow…
• First working implementation in mid-2010,
½ -hour to compute a single AND gate
– 13-14 orders of magnitude slowdown
vs. computing on non-encrypted data
• A faster “dumbed down” version
– Can only evaluate “very simple functions”
– About ½-second for an AND gate

Performance
• Underlying “somewhat homomorphic” scheme
• PK is 2 integers, SK is one integer
Dimension KeyGen Enc Dec / AND
(amortized)
2048 1.25 sec 60 millisec 23 millisec
Small

800,000-bit
integers
Medium

8192 10 sec 0.7 sec 0.12 sec
3,200,000-bit
integers

32768 95 sec 5.3 sec 0.6 sec
Large

13,000,000-bit
integers

Performance
• Fully homomorphic scheme

Dimension KeyGen PK size AND

2048 40 sec 70 MByte 31 sec
Small

800,000-bit
integers
Medium

8192 8 min 285 MByte 3 min
3,200,000-bit
integers

32768 2 hours 2.3 GByte 30 min
Large

13,000,000-bit
integers

Performance
• A little slow…
• Butler Lampson: “I don’t think we’ll see
anyone using Gentry’s solution in our
lifetimes *…+” – Forbes, Dec-19, 2011

New Stuff
• New techniques suggested during 2011
• Promise ~3 orders of magnitude improvement
vs. Gentry’s original scheme
– Implementations on the way
• Still very expensive, but maybe suitable for
some niche applications
• Computing “simple functions” using these
tools may be realistic

Things we can already use today
• Sometimes simple functions is all we need
– Statistics, simple keyword match, etc.
• Interactive solutions are sometime faster
– vs. the single round trip of Homomorphic Enc
• Great efficiency gains when settling for
weaker notions of secrecy
– “Order preserving encryption”
– MIT’s CryptDB (onion encryption)

Limitations of function-as-circuit
• Some performance optimizations are ruled out
• Example: Binary search
– log(n) steps to find element in an n-element array
– But circuit must be of size ~n
• Example: private information retrieval
– Non-encrypted access with one lookup
– But encrypted access must touch all entries
• Else you leak information (element is not in i’th entry)
• Only data-oblivious computation is possible

The [Gentry 2009] blueprint
Evaluate any function in four “easy” steps
• Step 1: Encryption from linear ECCs
– Additive homomorphism Error-Correcting Codes
• Step 2: ECC lives inside a ring
– Also multiplicative homomorphism
– But only for a few operations (low-degree poly’s)
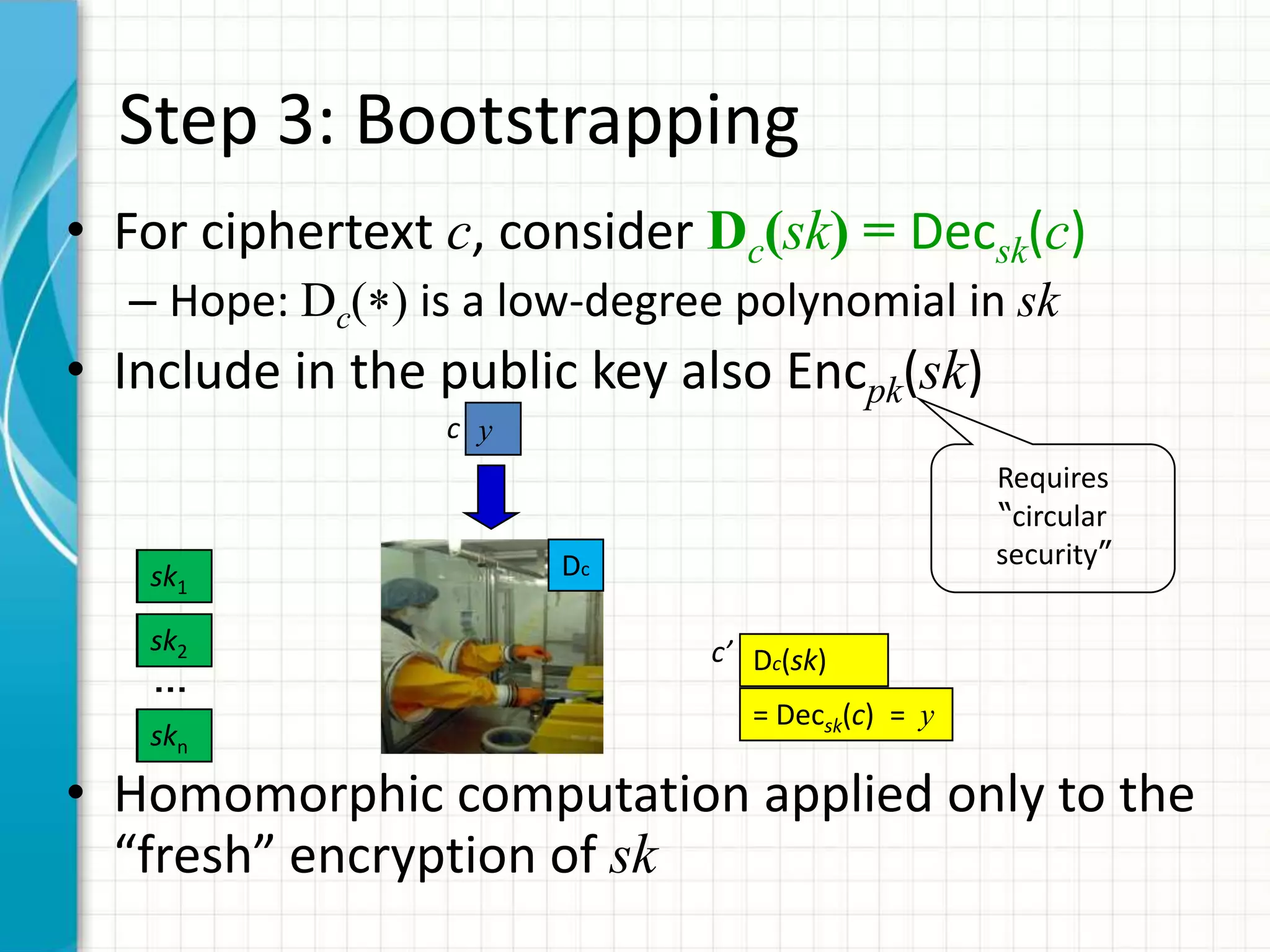
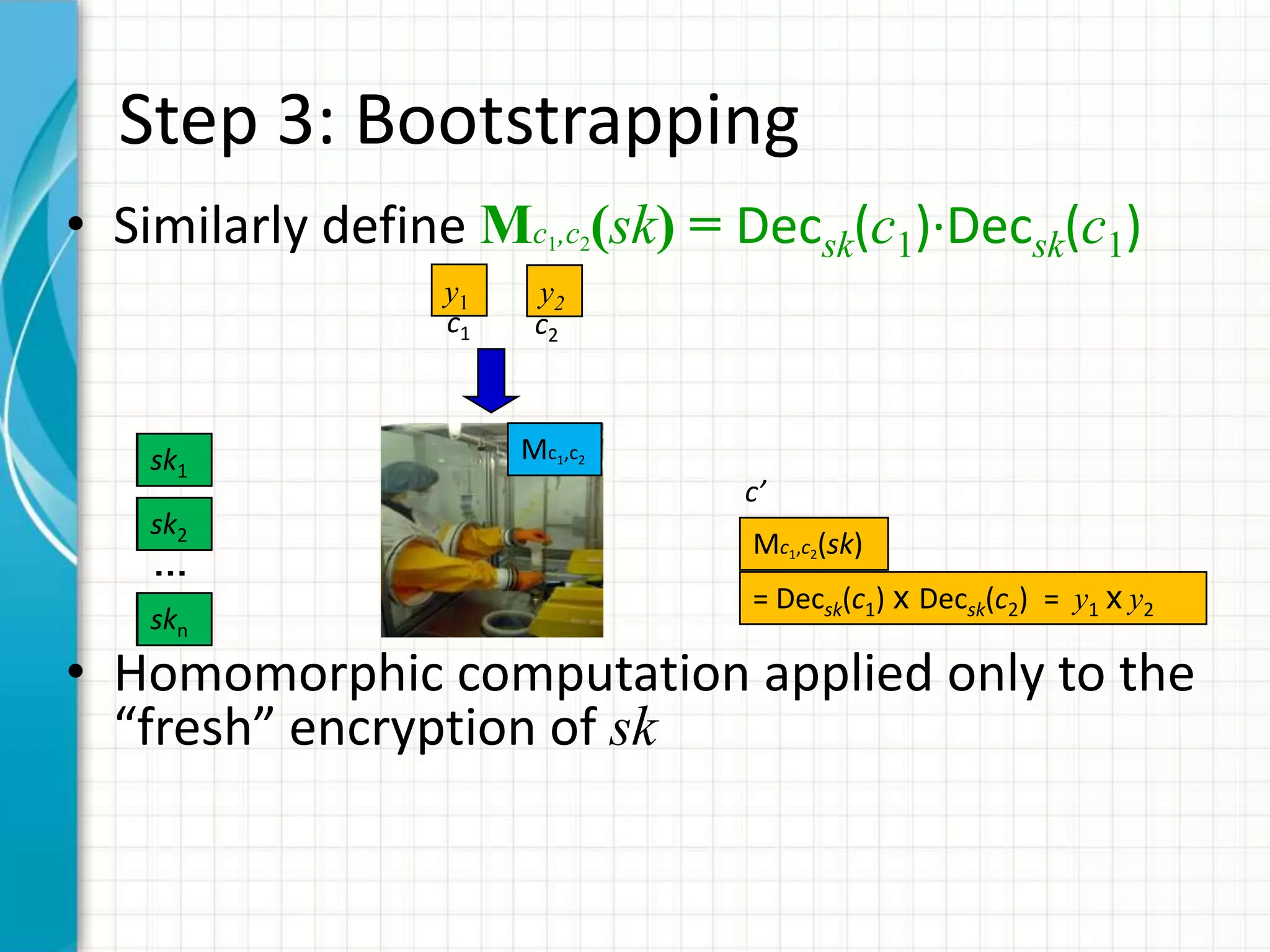
• Step 3: Bootstrapping
– Few ops (but not too few)  any number of ops
• Step 4: Everything else
– “Squashing” and other fun activities

Step 1: Encryption from Linear ECCs
• For “random looking” codes, hard to
distinguish close/far from code

• Many cryptosystems built on this hardness
– E.g., *McEliece’78, AD’97, GGH’97, R’03,…+

Step 1: Encryption from Linear ECCs
• KeyGen: choose a “random” Code
– Secret key: “good representation” of Code
• Allows correction of “large” errors
– Public key: “bad representation” of Code
• Can generate “random code-words”
• Hard to distinguish close/far from the code
• Enc(0): a word close to Code
• Enc(1): a random word
– Far from Code (with high probability)

Example: Integers mod p [vDGHV 2010]
p N

• Code determined by a secret integer p
– Codewords: multiples of p
• Good representation: p itself
• Bad representation: ri << p
– N = pq, and also many xi = pqi + ri
• Enc(0): subset-sum(xi’s)+r mod N
– r is new noise, chosen by encryptor
• Enc(1): random integer mod N

A Different Input Encoding
p N
xi = pqi + ri
• Both Enc(0), Enc(1) close to the code
– Enc(0): distance to code is even Plaintext encoded
– Enc(1): distance to code is odd in the “noise”

– Security unaffected when p is odd

• In our example of integers mod p:
– Enc(b) = 2(r+subset-sum(xi’s)) + b mod N
= p + 2(r+subset-sum(ri’s))+b
much smaller
than p/2
– Dec(c) = (c mod p) mod 2

Additive Homomorphism
• c1+c2 = (codeword1+codeword2)
+ (2r1+b1)+(2r2+b2 )
– codeword1+codeword2 Code
– (2r1+b1)+(2r2+b2 )=2(r1+r2)+b1+b2 is still small
• If 2(r1+r2)+b1+b2 < min-dist/2, then
dist(c1+c2, Code) = 2(r1+r2)+b1+b2
 dist(c1+c2, Code) b1+b2 (mod 2)
• Additively-homomorphic while close to Code

Step 2: Code Lives in a Ring
• What happens when multiplying in Ring:
– c1∙c2 = (codeword1+2r1+b1)∙(codeword2+2r2+b2)
= codeword1∙X + Y∙codeword2
+ (2r1+b1)∙(2r2+b2) Code is an ideal
• If:
– codeword1∙X + Y∙codeword2 Code
– (2r1+b1)∙(2r2+b2) < min-dist/2
Product in Ring of
• Then small elements is small
– dist(c1c2, Code) = (2r1+b1)∙(2r2+b2) = b1∙b2 mod 2

Example: Integers mod p [vDGHV 2010]
p N
xi = pqi + ri
• Secret-key is p, public-key is N and the xi’s
• ci = Encpk(bi) = 2(r+subset-sum(xi’s)) + b mod N
= kip + 2ri+bi
– Decsk(ci) = (ci mod p) mod 2
• c1+c2 mod N = (k1p+2r1+b1)+(k2p+2r2+b2) – kqp
= k’p + 2(r1+r2) + (b1+b2)
• c1c2 mod N = (k1p+2r1+b1)(k2p+2r2+b2) – kqp
= k’p + 2(2r1r2+r1b2+r2b1)+b1b2
• Additive, multiplicative homomorphism
– As long as noise < p/2

Summary Up To Now
• We need a linear error-correcting code C
– With “good” and “bad” representations
– C lives inside an algebraic ring R
– C is an ideal in R
– Sum, product of small elements in R is still small
• Can find such codes in Euclidean space
– Often associated with lattices
• Then we get a “somewhat homomorphic”
encryption, supporting low-degree polynomials
– Homomorphism while close to the code

Step 3: Bootstrapping
• So far, can evaluate low-degree polynomials
x1 P
x2
… P(x1, x2 ,…, xt)

xt

x1 P
x2
… P(x1, x2 ,…, xt)

xt

• Can eval y=P(x1,x2…,xn) when xi’s are “fresh”
• But y is an “evaluated ciphertext”
– Can still be decrypted
– But eval Q(y) will increase noise too much
• “Somewhat Homomorphic” encryption (SWHE)

x1 P
x2
… P(x1, x2 ,…, xt)

xt

• Bootstrapping to handle higher degrees
– We have a noisy evaluated ciphertext y
– Want to get another y with less noise

• For ciphertext c, consider Dc(sk) = Decsk(c)
– Hope: Dc( ) is a low-degree polynomial in sk
• Include in the public key also Encpk(sk)
c y
Requires
“circular
Dc security”
sk1

sk2 c’ Dc(sk)
…
= Decsk(c) = y
skn

• Homomorphic computation applied only to the
“fresh” encryption of sk

• Similarly define Mc ,c (sk) = Decsk(c1)∙Decsk(c1)
1 2

y1 y2
c1 c2

sk1 Mc1,c2
c’
sk2
Mc1,c2(sk)
…
= Decsk(c1) x Decsk(c2) = y1 x y2
skn
• Homomorphic computation applied only to the
“fresh” encryption of sk

Step 4: Everything Else
• Cryptosystems from *G’09, vDGHV’10, BG’11a]
cannot handle their own decryption
• Tricks to “squash” the decryption
procedure, making it low-degree
– Nontrivial, requires putting more information
about the secret key in the public key
– Requires yet another assumption, namely hardness
of the Sparse-Subset-Sum Problem (SSSP)
– I will not talk about squashing here

Computing on Encrypted Data

More Related Content

What's hot

Similar to Computing on Encrypted Data

More from New York Technology Council

Recently uploaded

Computing on Encrypted Data