Data structure and algorithm list structures

Data Structures and Algorithms
UNIT-II-List Structure

Syllabus
Operations on List ADT – Create, Insert, Search, Delete, Display
elements; Implementation of List ADT – Array, Cursor based and
Linked Types – Singly, Doubly, Circular; Applications - Sparse Matrix,
Polynomial Arithmetic, Joseph Problem

Operations on List ADT
ADT = properties + operations
• An ADT describes a set of objects sharing the same properties and
behaviors
• The properties of an ADT are its data (representing the internal state of each
object
• double d; -- bits representing exponent & mantissa are its data or state
• The behaviors of an ADT are its operations or functions (operations on each
instance)
• sqrt(d) / 2; //operators & functions are its behaviors

The List ADT
 A sequence of zero or more elements A1, A2, A3, … AN
 N: length of the list
 A1: first element
 AN: last element
 Ai: position i
 If N=0, then empty list
 Linearly ordered
 Ai precedes Ai+1
 Ai follows Ai-1

Operations
 makeEmpty: create an empty list
 find: locate the position of an object in a list
 list: 34,12, 52, 16, 12
 find(52)  3
 insert: insert an object to a list
 insert(x,3)  34, 12, 52, x, 16, 12
 remove: delete an element from the list
 remove(52)  34, 12, x, 16, 12
 findKth: retrieve the element at a certain position
 printList: print the list

Implementation of an ADT
• Choose a data structure to represent the ADT
• E.g. arrays, records, etc.
• Each operation associated with the ADT is implemented by one or
more subroutines
• Two standard implementations for the list ADT
• Array-based
• Linked list

Array Implementation
• Elements are stored in contiguous array positions

1D Array Representation
• 1-dimensional array x = [a, b, c, d]
• map into contiguous memory locations

2D Arrays
• The elements of a 2-dimensional array a declared as:
int a[3][4] ;
• may be shown as a table
a[0][0] a[0][1] a[0][2] a[0][3]
a[1][0] a[1][1] a[1][2] a[1][3]
a[2][0] a[2][1] a[2][2] a[2][3]

Linear List Array Representation
• use a one-dimensional array called alphabet[]
• List = (a, b, c, d, e)
• Store element I of list in alphabet[i]

Array Applications
• Stores Elements of Same Data Type
• Array Used for Maintaining multiple variable names using single name
• Array Can be Used for Sorting Elements
• Array Can Perform Matrix Operation
• Array Can be Used in CPU Scheduling
• Array Can be Used in Recursive Function

Array Implementation...
🞂 Requires an estimate of the maximum size of the list
⮚ waste space
🞂 printList and find: O(n)
🞂 findKth: O(k)
🞂 insert and delete: O(n)
🞂 e.g. insert at position 0 (making a new element)
🞂 requires first pushing the entire array down one spot to make room
🞂 e.g. delete at position 0
🞂 requires shifting all the elements in the list up one
🞂 On average, half of the lists needs to be moved for either
operation

• Array Declaration
• Int arr[10];
• b=10;
• int arr1[b];
• int [b+5];
• 2-D Array
• int arr2[4][5];

Dynamic array declaration
• int size_arr;
• scanf("&d",&size_arr);
• int *arr1 = (int*)malloc(sizeof(int)*size_arr);
• int p11[size];
• for(i = 0; i < size; i++ )
• { scanf("%d",&p11[i])
• }
• Or
• for(i = 0; i < size; i++ )
• { scanf("%d",(p11+i));
• }

Multi-dimensional SPARSE Matrix
• A matrix is a two-dimensional data object made of m
rows and n columns, therefore having m X n values.
When m=n, we call it a square matrix.
• There may be a situation in which a matrix contains
more number of ZERO values than NON-ZERO values.
Such matrix is known as sparse matrix.
• When a sparse matrix is represented with 2-
dimensional array, we waste lot of space to represent
that matrix.
• For example, consider a matrix of size 100 X 100
containing only 10 non-zero elements.

Contd…
• In this matrix, only 10 spaces are filled with non-zero values
and remaining spaces of matrix are filled with zero.
• totally we allocate 100 X 100 X 2 = 20000 bytes of space to
store this integer matrix.
• to access these 10 non-zero elements we have to make
scanning for 10000 times.
• If most of the elements in a matrix have the value 0, then the
matrix is called sparSe matrix.
Example For 3 X 3 Sparse Matrix:
•
| 1 0 0 |
| 0 0 0 |
| 0 4 0 |

Sparse Matrix Representations
• A sparse matrix can be represented by using TWO representations,
those are as follows...
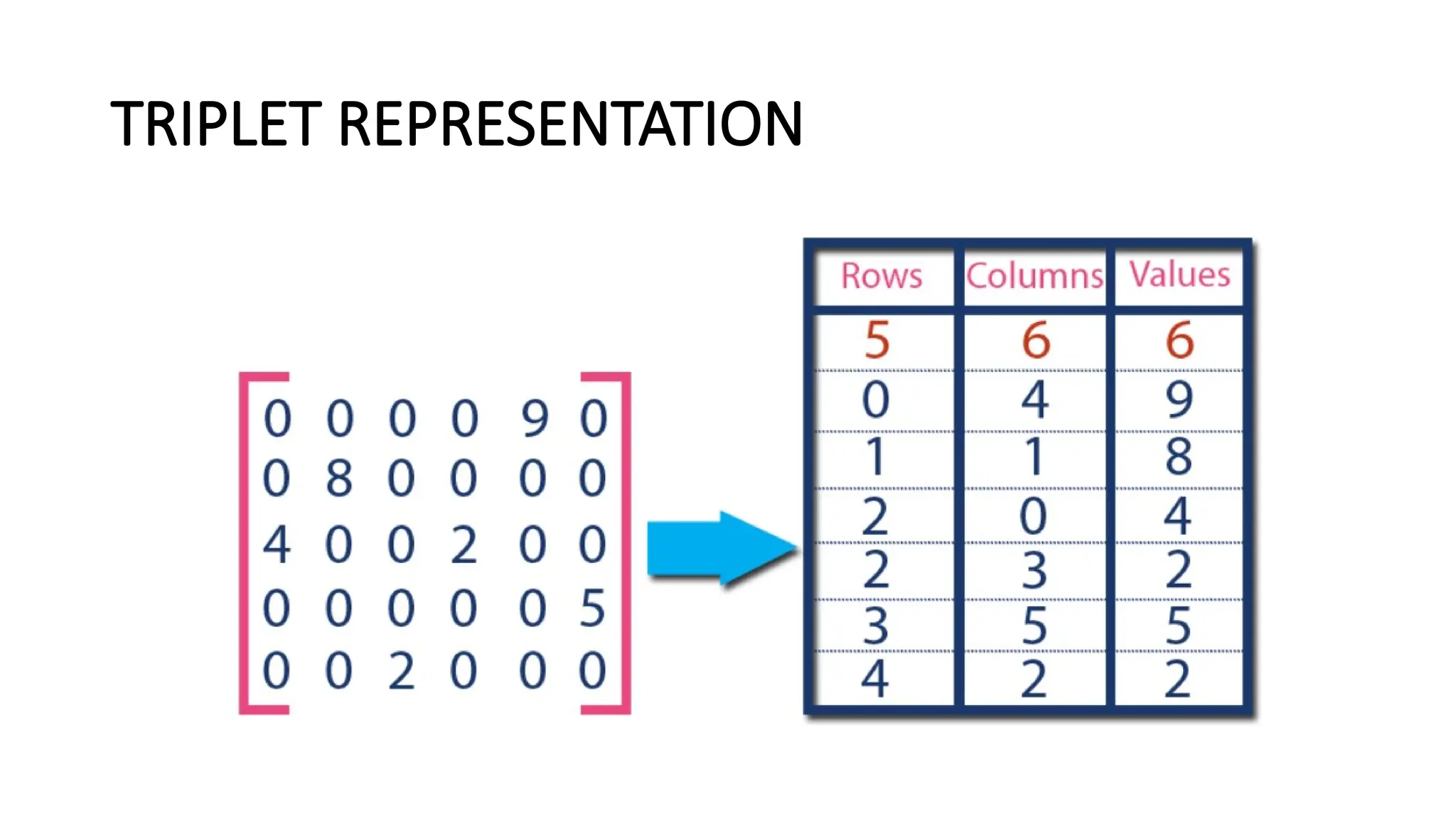
• Triplet Representation
• Linked Representation

TRIPLET REPRESENTATION (ARRAY REPRESENTATION)
• In this representation, only non-zero values are considered along with
their row and column index values.
• The array index [0,0] stores the total number of rows, [0,1] index
stores the total number of columns and [0,1] index has the total
number of non-zero values in the sparse matrix.
• For example, consider a matrix of size 5 X 6 containing 6 number of
non-zero values.

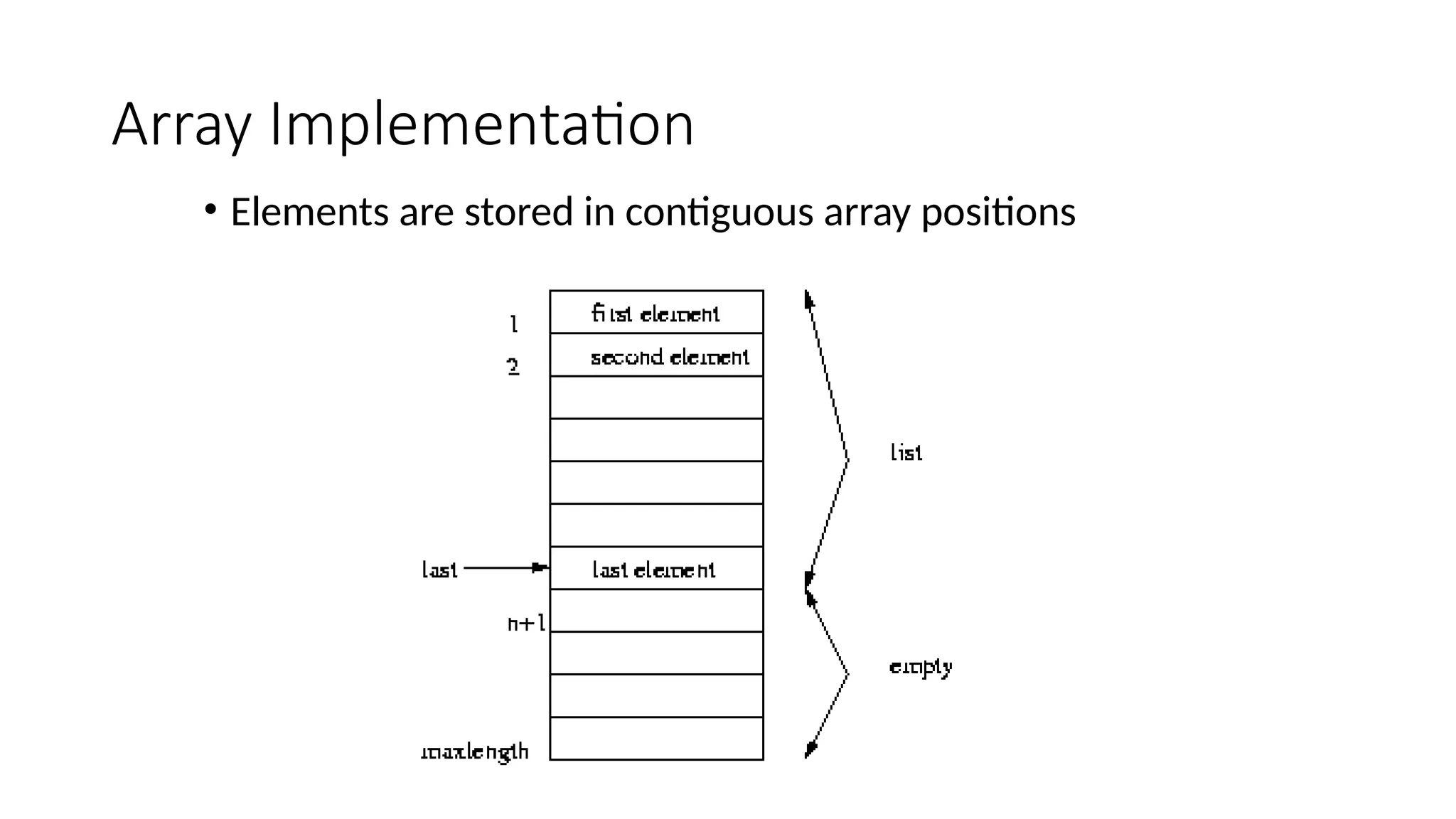
Array Implementation
for(i=0;i<m;i++)
{
for(j=0;j<n;j++)
{
printf("%d ",Arr[i][j]);
}
printf("n");
}
for(i=0;i<m;i++)
{
for(j=0;j<n;j++)
{
if(Arr[i][j]!=0)
{
B1[s1][0]=Arr[i][j];
B1[s1][1]=i;
B1[s1][2]=j;
s1++;} }
}

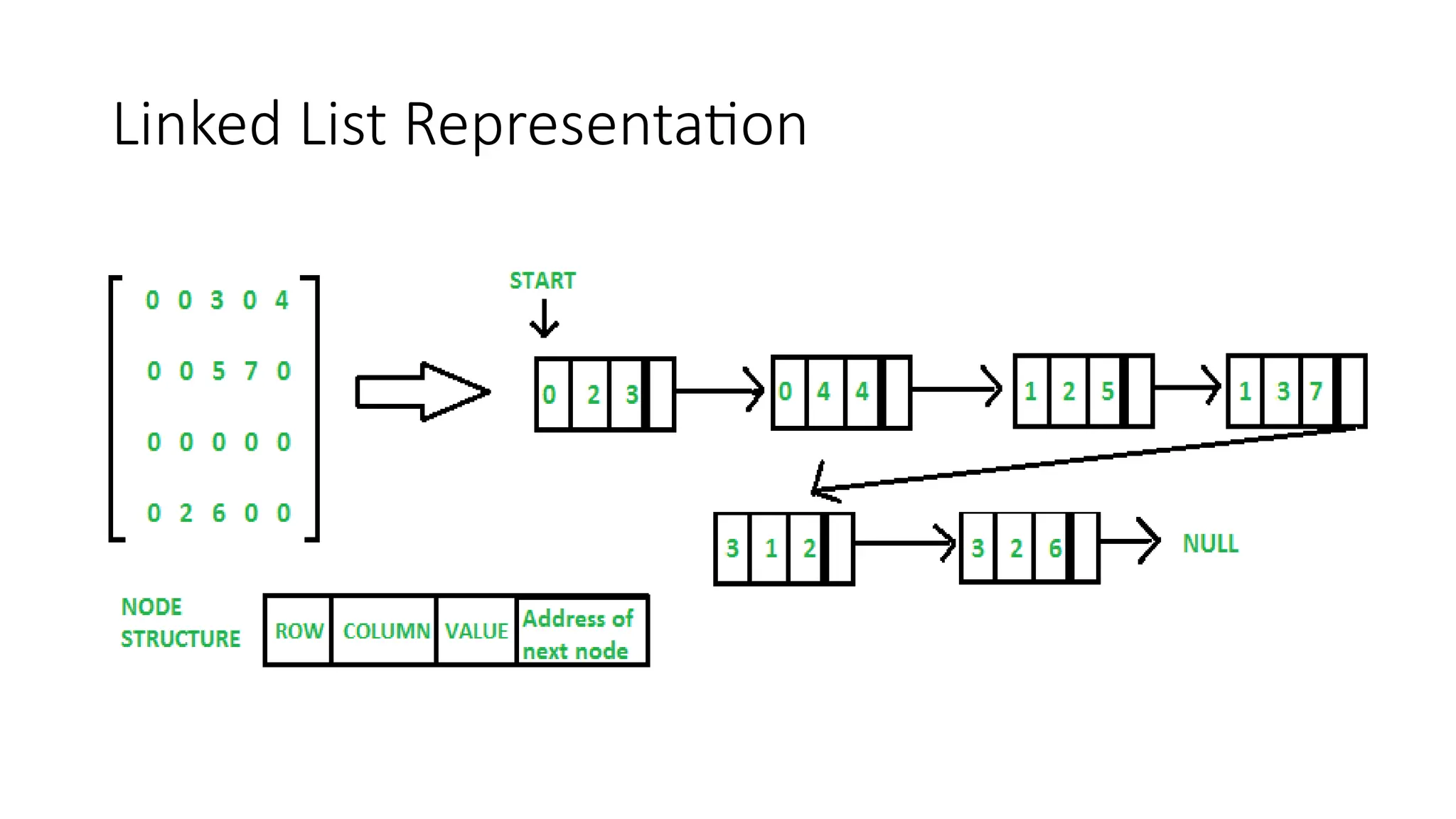
Linked List Representation
• In linked list representation, a linked list data structure is used to
represent a sparse matrix.
• In linked list, each node has four fields. These four fields are defined
as:
• Row: Index of row, where non-zero element is located
• Column: Index of column, where non-zero element is located
• Value: Value of the non zero element located at index – (row,column)
• Next node: Address of the next node

Cursor Implementation
• Some programming languages doesn’t support pointers.
• But we need linked list representation to store data.
• Solution:
• Cursor implementation – implementing linked list on an array.
• Main idea is:
• Convert a linked list based implementation to an array based
implementation.
• Instead of pointers, array index could be used to keep track of node.
• Convert the node structures (collection of data and next pointer) to
a global array of structures.
• Need to find a way to perform dynamic memory allocation
performed using malloc and free functions.

Declarations for cursor implementation of
linked lists

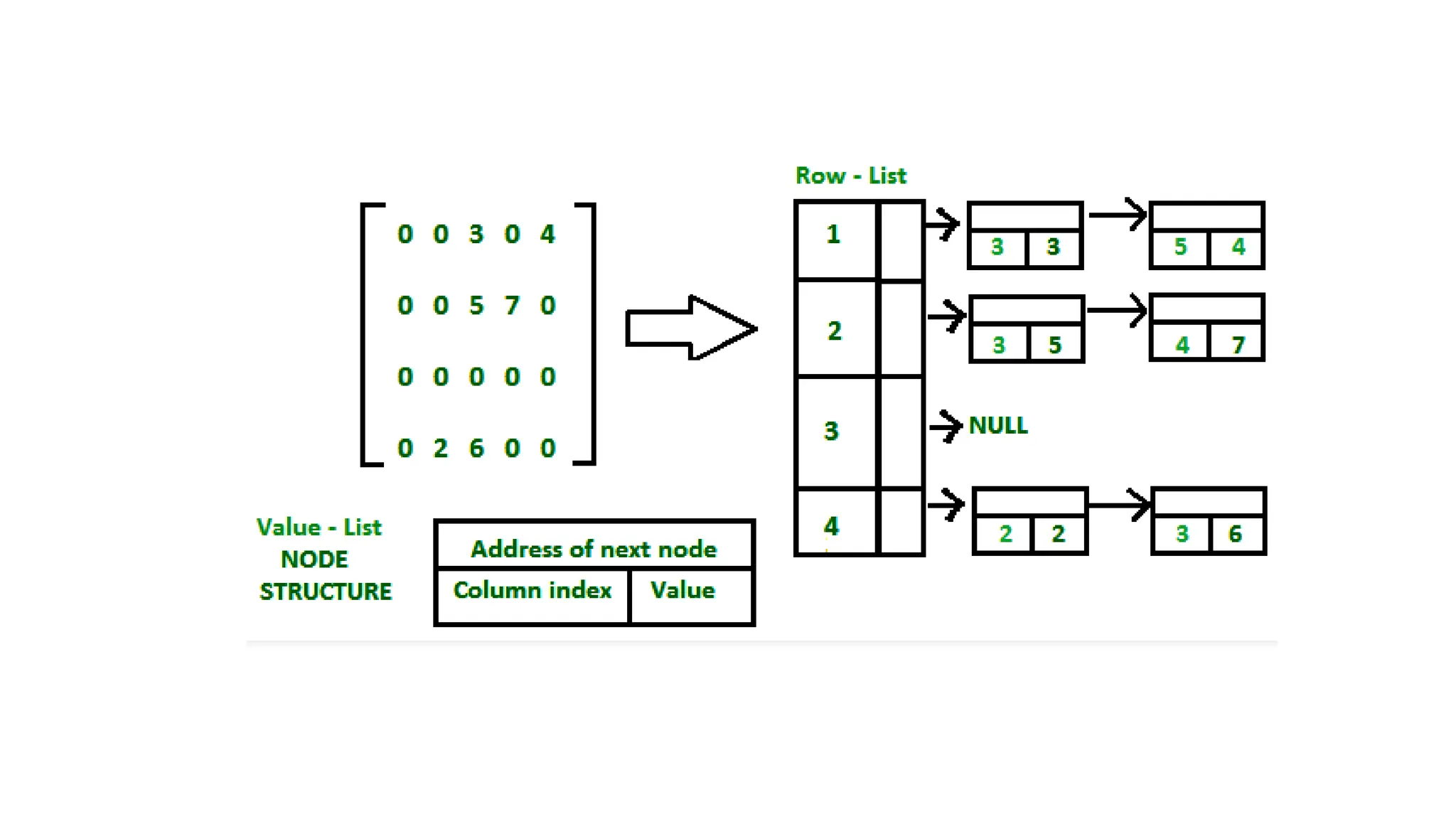
Initializing Cursor Space
• Cursor_space[list] =0;
• To check whether cursor_space is empty:
• To check whether p is last in a linked list

Data structure and algorithm list structures

More Related Content

Similar to Data structure and algorithm list structures

Recently uploaded

Data structure and algorithm list structures