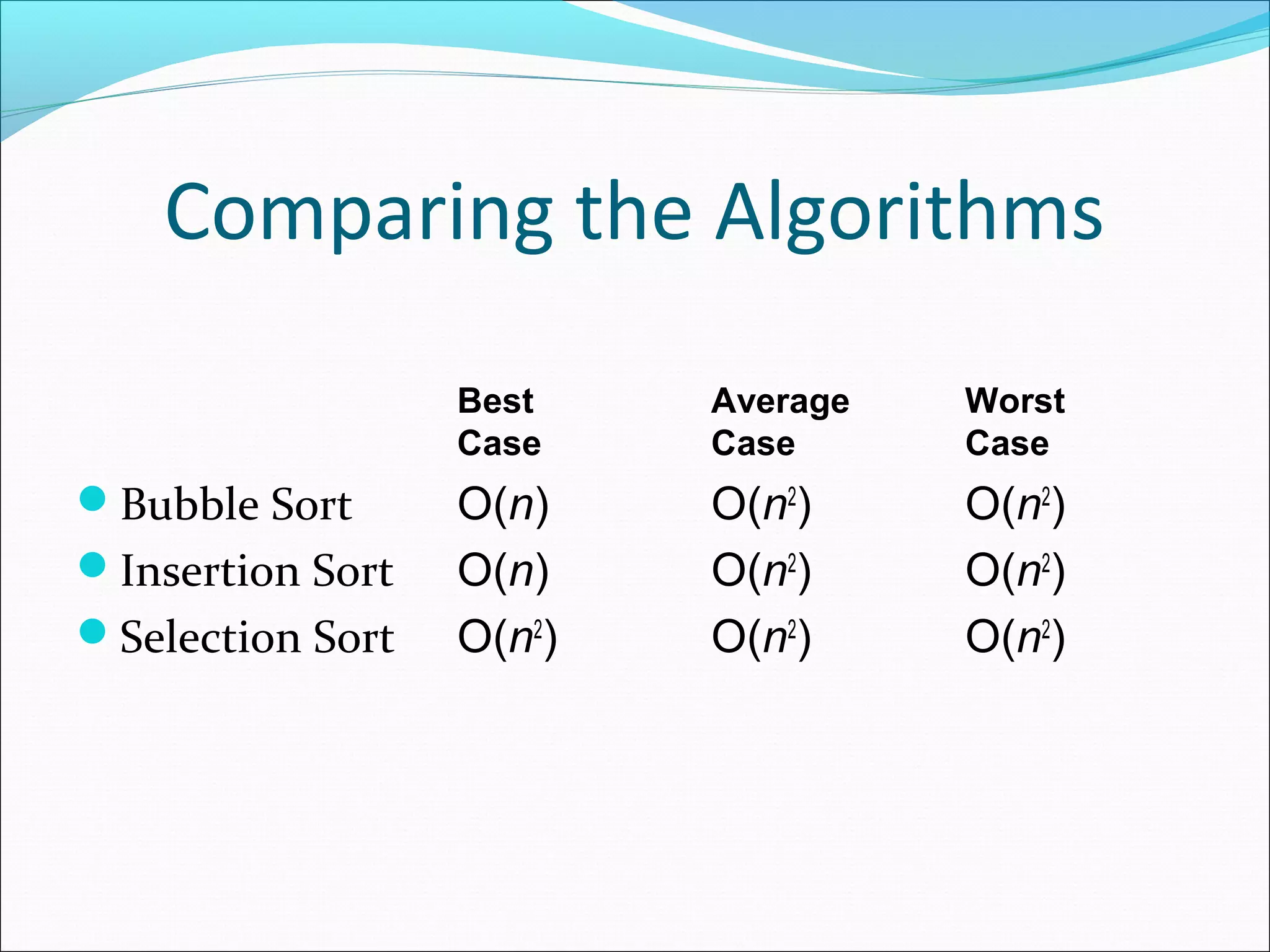
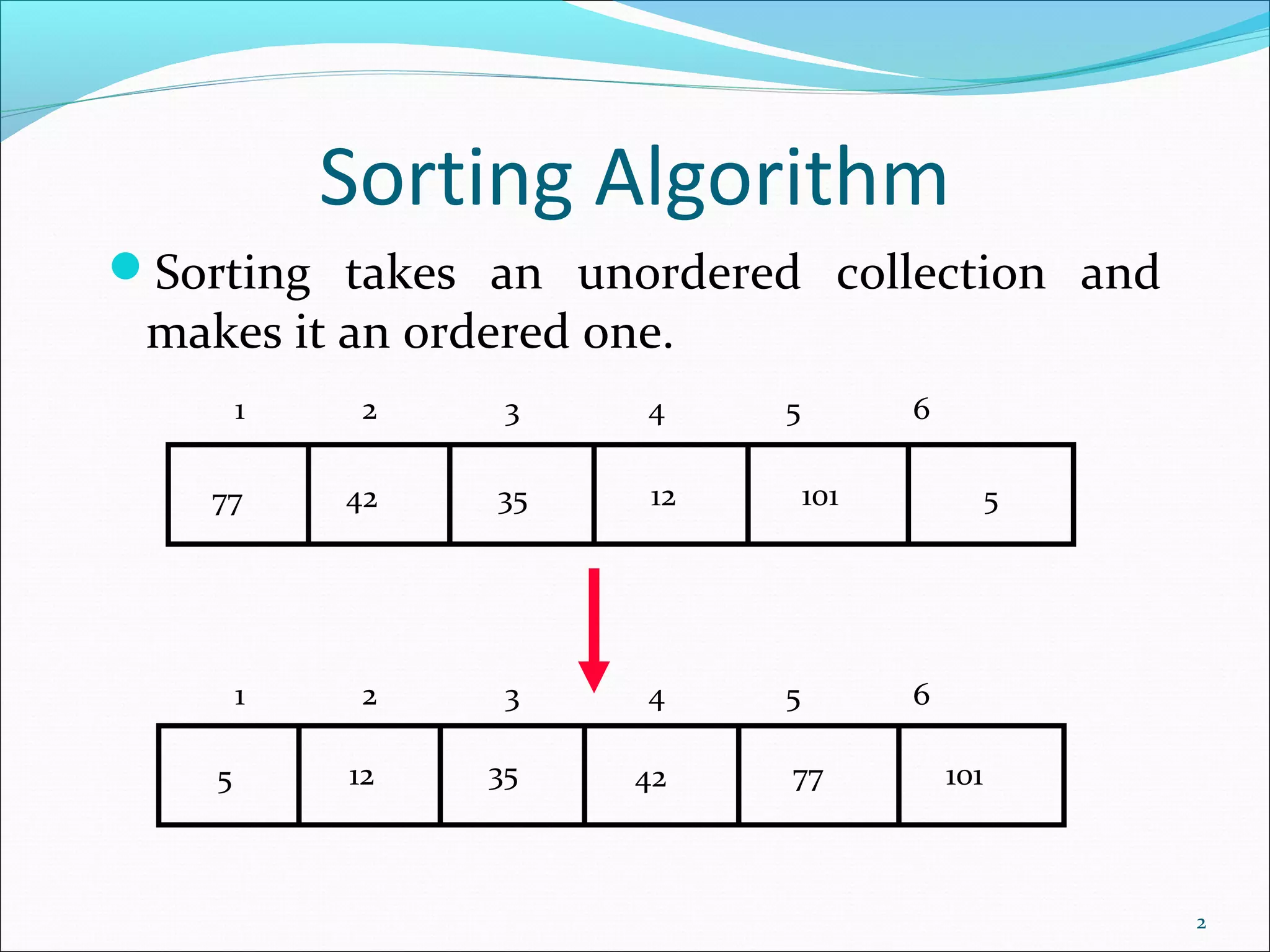
The document describes three sorting algorithms: bubble sort, insertion sort, and selection sort. Bubble sort works by traversing a list from the beginning to end and swapping adjacent elements to bubble the largest values to the end over multiple passes until the list is fully sorted. Insertion sort iterates through a list and inserts each element into its sorted position by shifting other elements over. Selection sort finds the minimum element on each pass and swaps it into the front of the partially sorted list. All three algorithms have a worst-case quadratic runtime of O(n^2).










![Bubble Sort
Algorithm
for i 1 to n-1 do
for j 1 to n-i do
if (A[j+1] < A[j]) swap A[j] and A[j+1] ;
}
}
Analysis:
In general, if the list has n elements, we will have to do
(n-1) + (n-2) …. + 2 +1 = (n-1) n / 2 comparisons.
=O(n^2)
12](https://image.slidesharecdn.com/ds3-sorting-180827163439/75/Data-Structure-and-Algorithms-Sorting-12-2048.jpg)
![Insertion Sort
INSERTION_SORT (A, N)
1.Set A[0] = -∞.
2.Repeat Step 3 to 5 for K = 2, 3, …, N:
3. Set TEMP = A[K] and PTR = K – 1.
4. Repeat while TEMP < A[PTR]:
(a) Set A[PTR+1] = A[PTR]
(b) Set PTR = PTR – 1.
[End of Loop.]
5. Set A[PTR+1] = TEMP.
[End of Loop 2.]
6.Return.](https://image.slidesharecdn.com/ds3-sorting-180827163439/75/Data-Structure-and-Algorithms-Sorting-13-2048.jpg)


![Selection Sort
This algorithm sorts an array A with N elements.
SELECTION(A, N)
1.Repeat steps 2 and 3 for k=1 to N-1:
2. Call MIN(A, K, N, LOC).
3. [Interchange A[k] and A[LOC]]
Set Temp:= A[k], A[k]:= A[LOC] and A[LOC]:=Temp.
[End of step 1 Loop.]
1.Exit.
MIN(A, K, N, LOC).
1.Set MIN := A[K] and LOC:= K.
2.Repeat for j=k+1 to N:
If Min>A[j], then: Set Min:= A[j] and LOC:=J.
[End of if structure]
3.Return.](https://image.slidesharecdn.com/ds3-sorting-180827163439/75/Data-Structure-and-Algorithms-Sorting-16-2048.jpg)