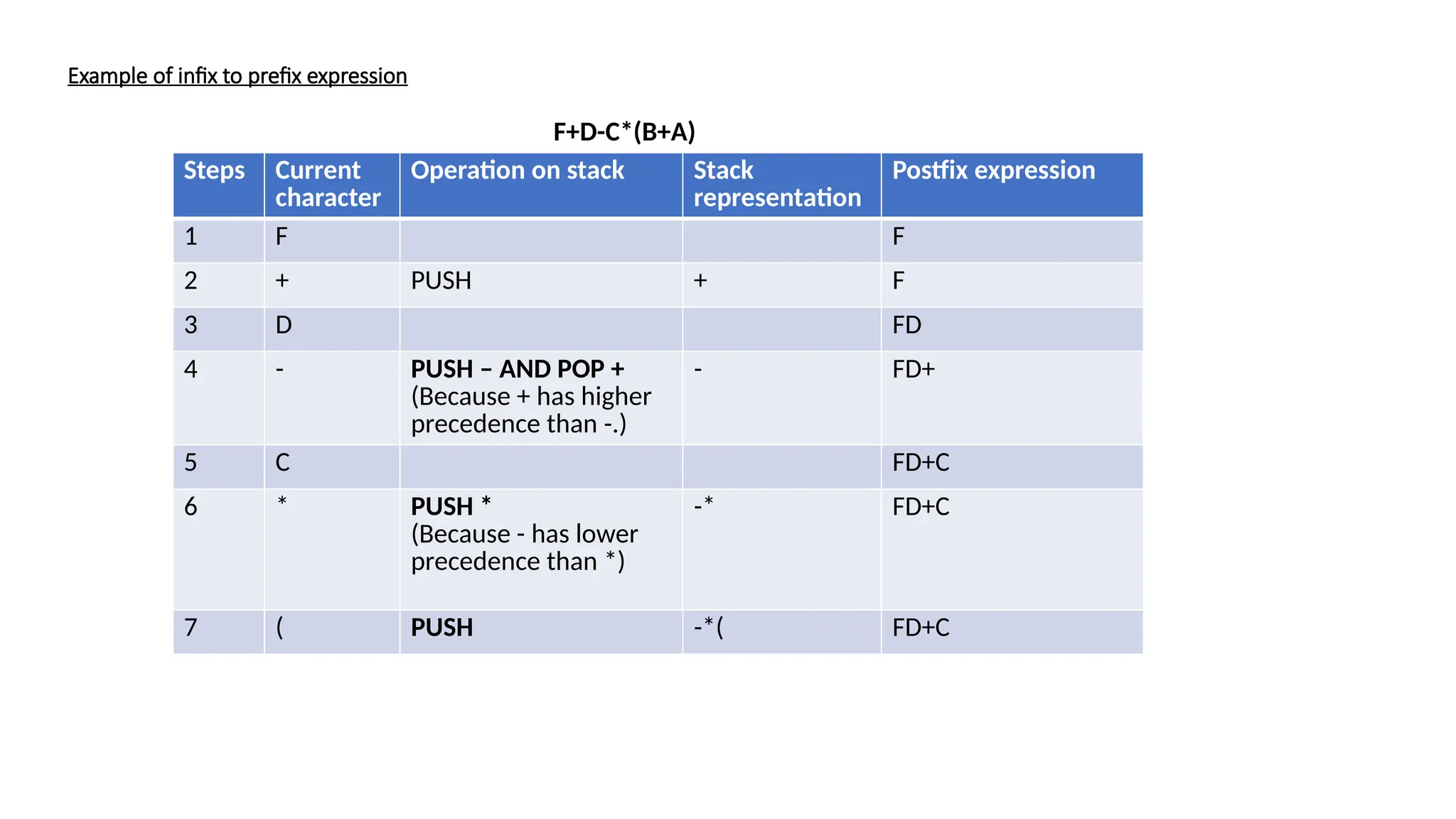
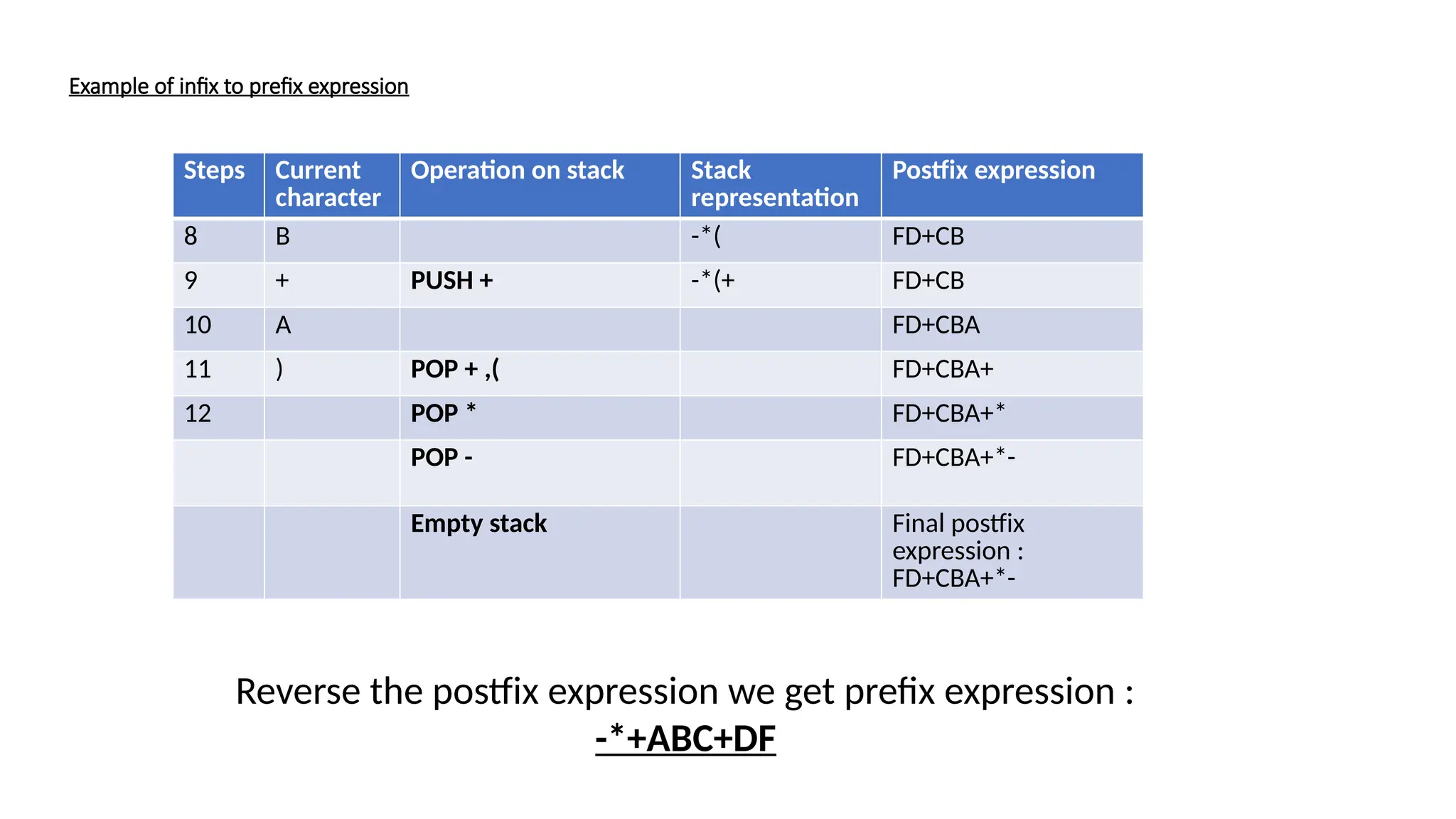
The document explains the terminology and processes involved in converting infix expressions to prefix and postfix formats using stacks. Key terms include infix, prefix, postfix, and reverse Polish notation, along with detailed steps for converting an infix expression. An example illustrates the conversion process, emphasizing how to maintain operator precedence and associativity.