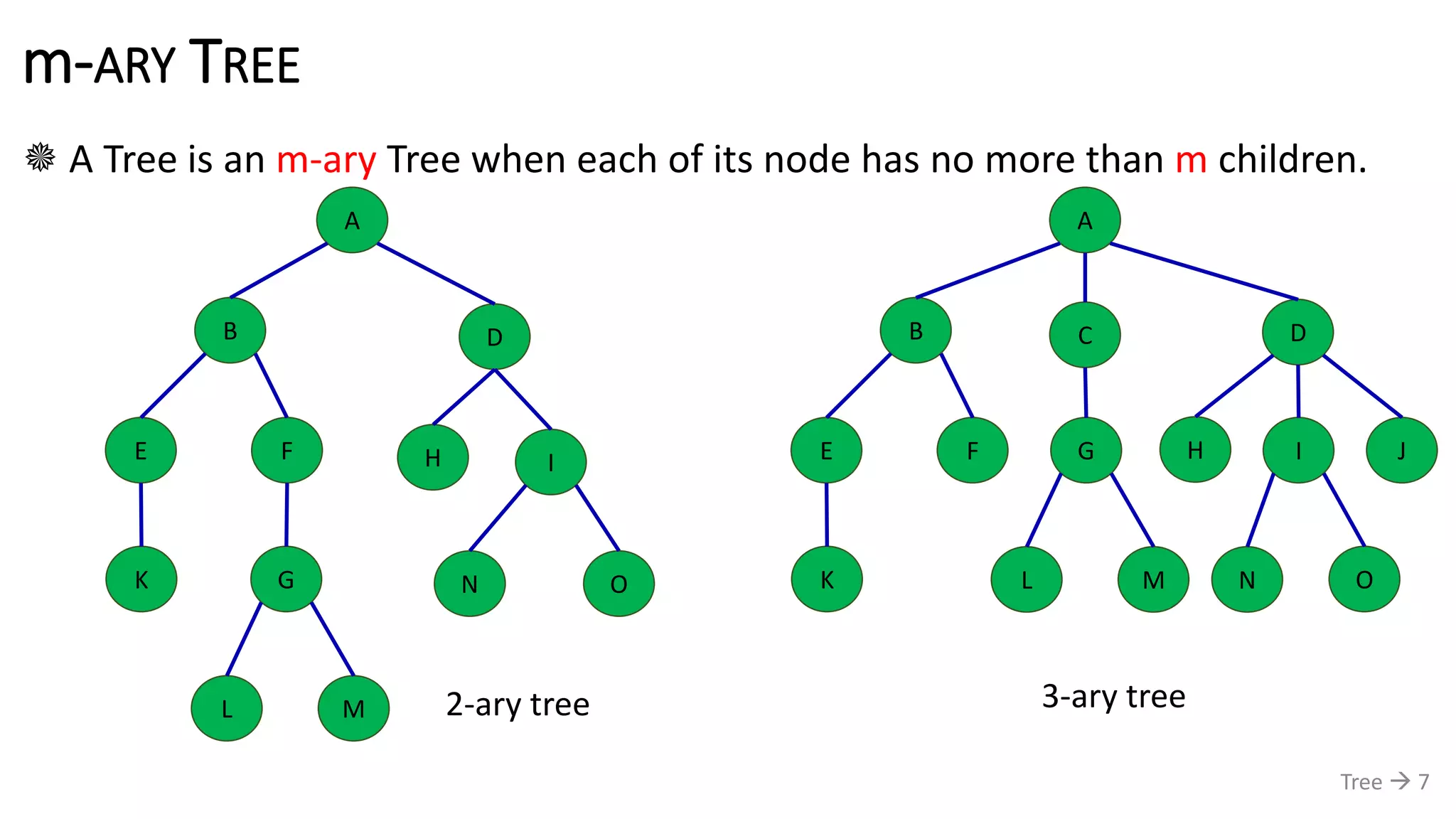
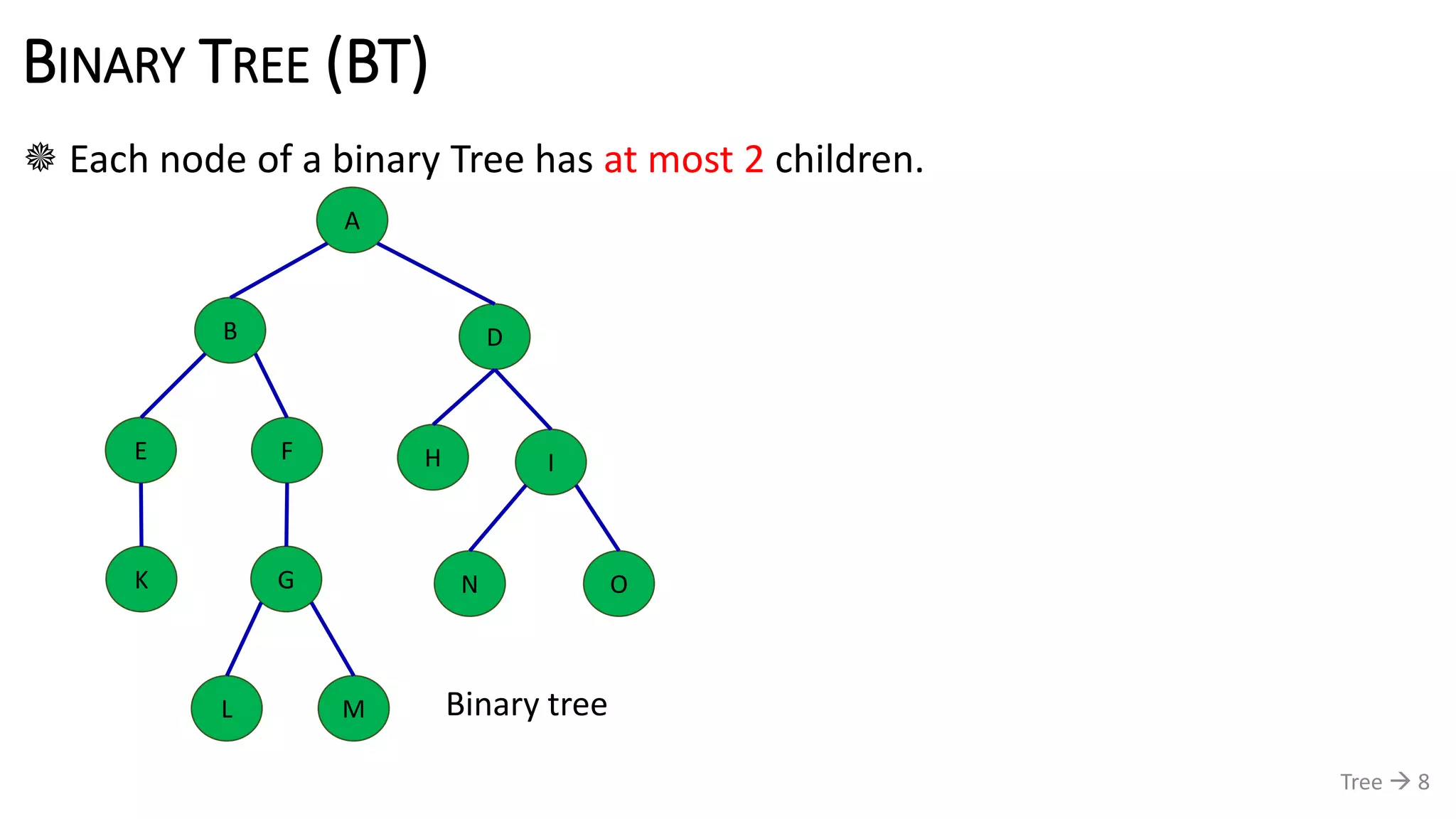
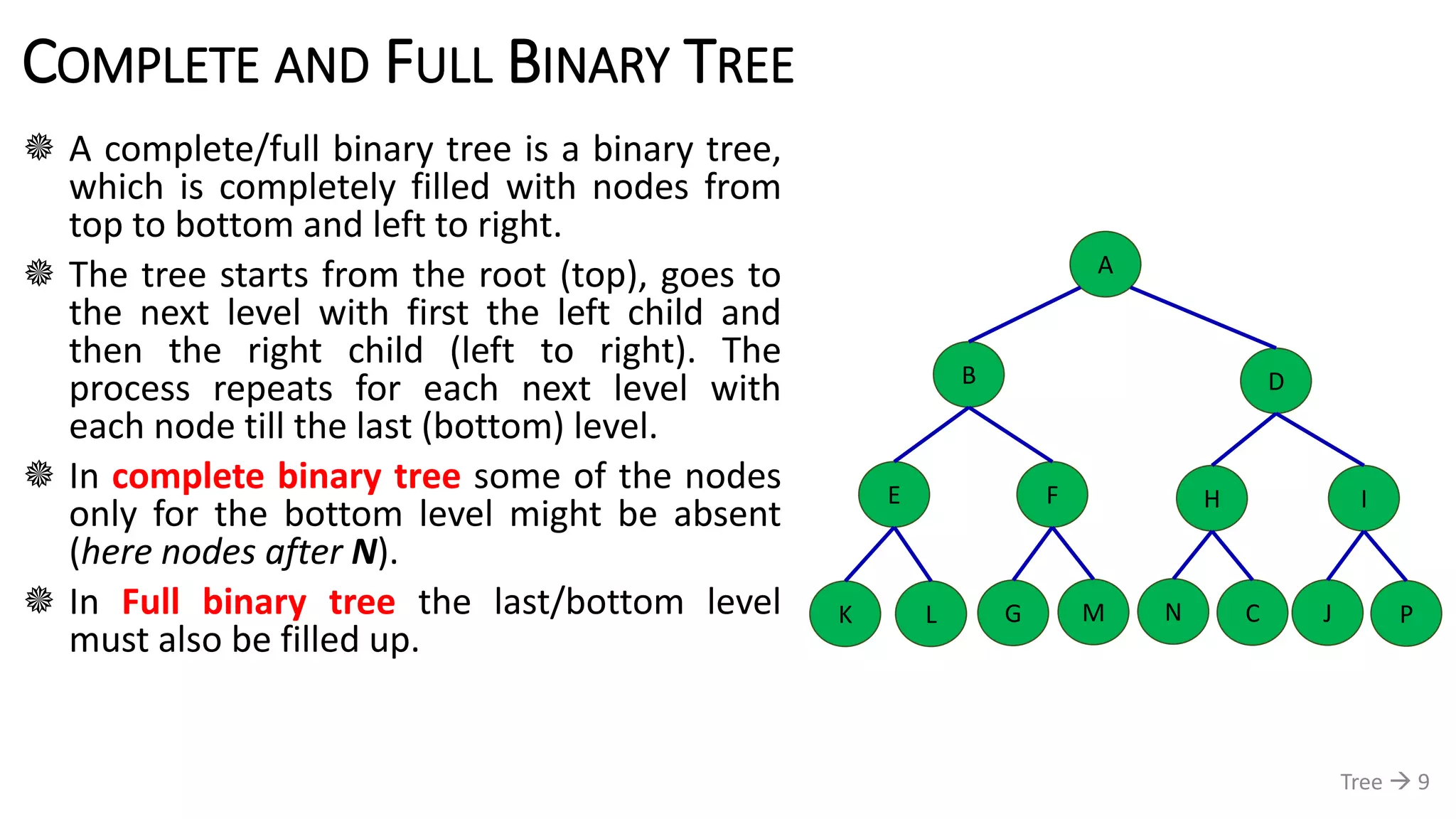
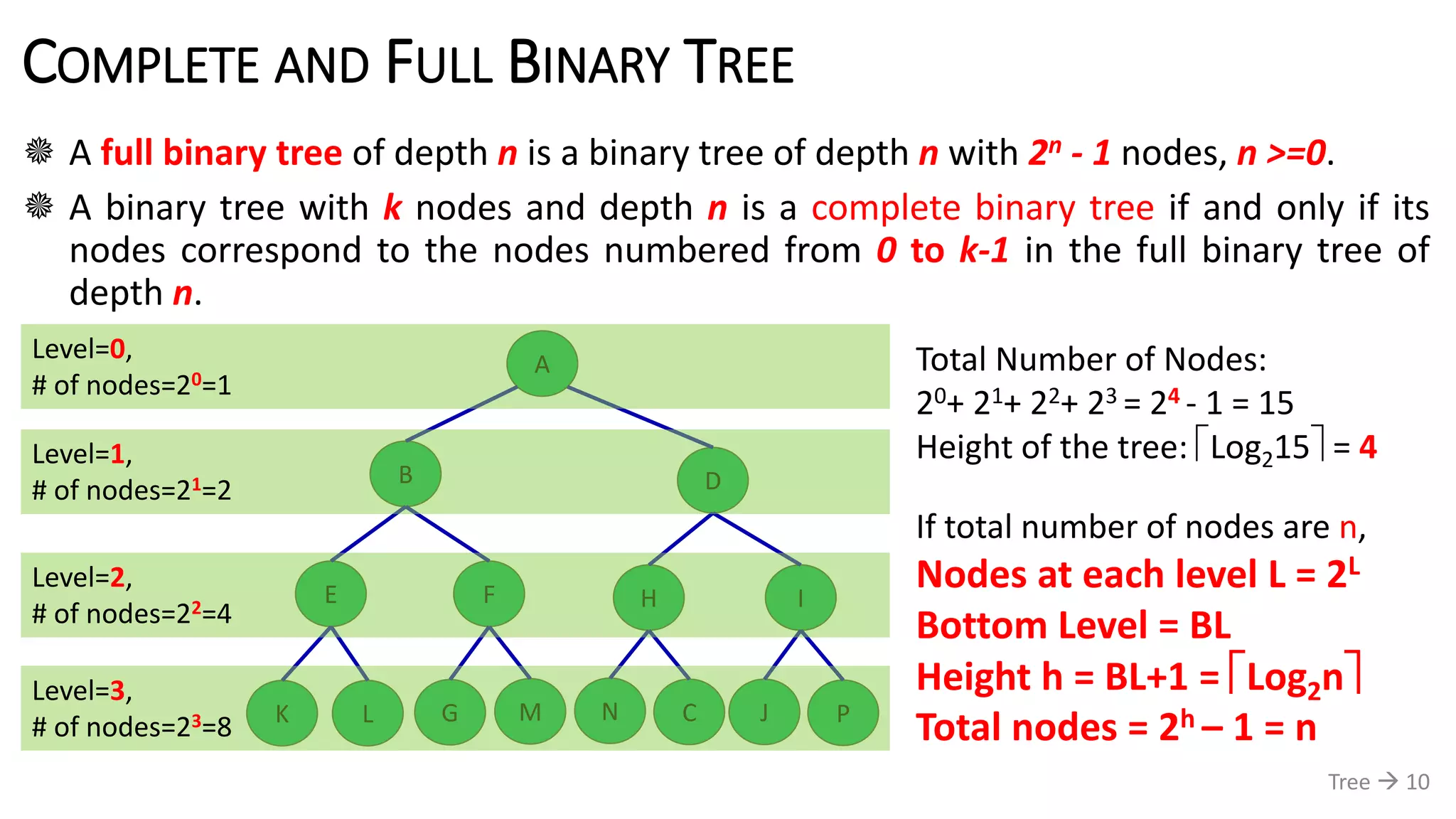
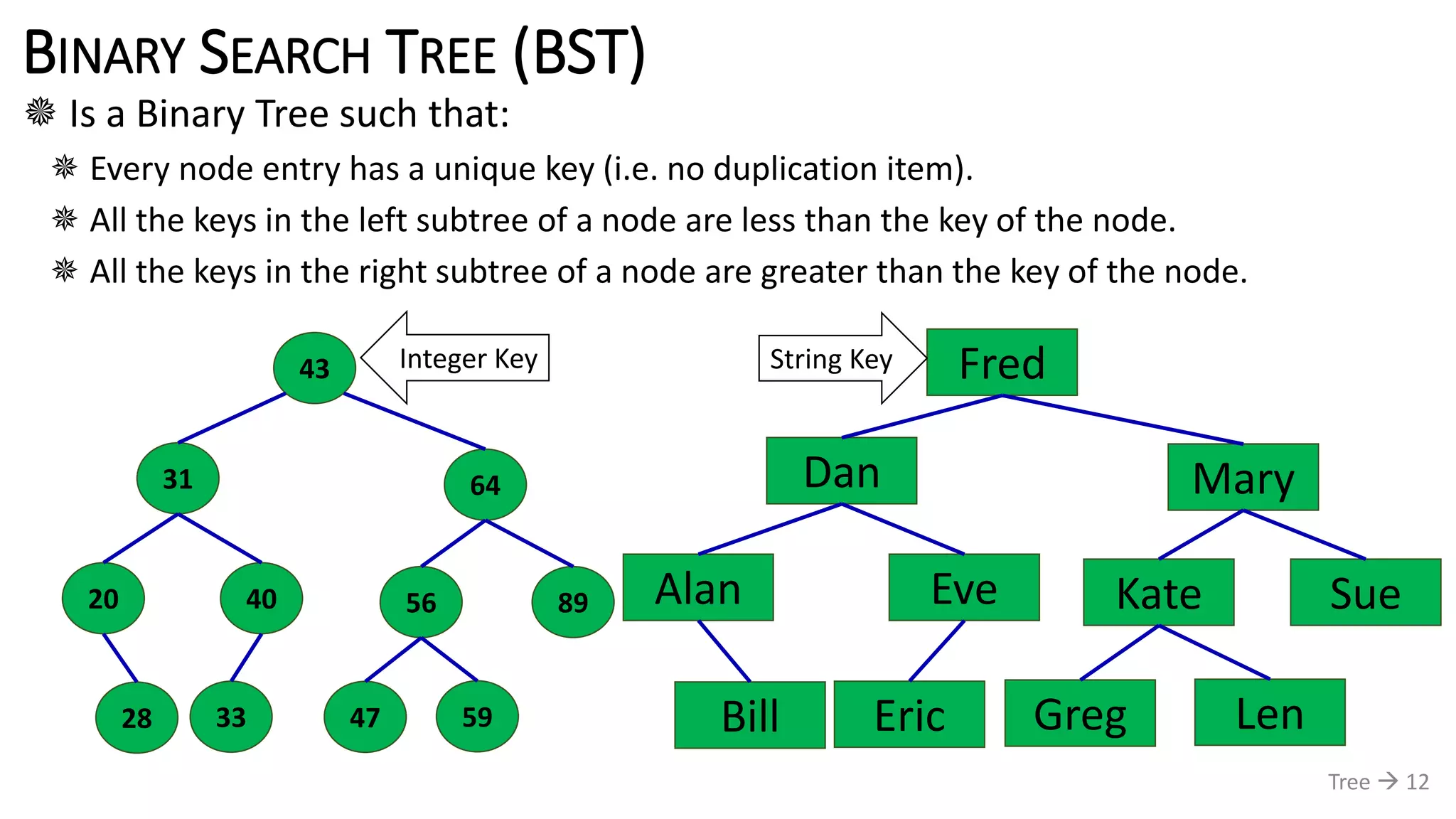
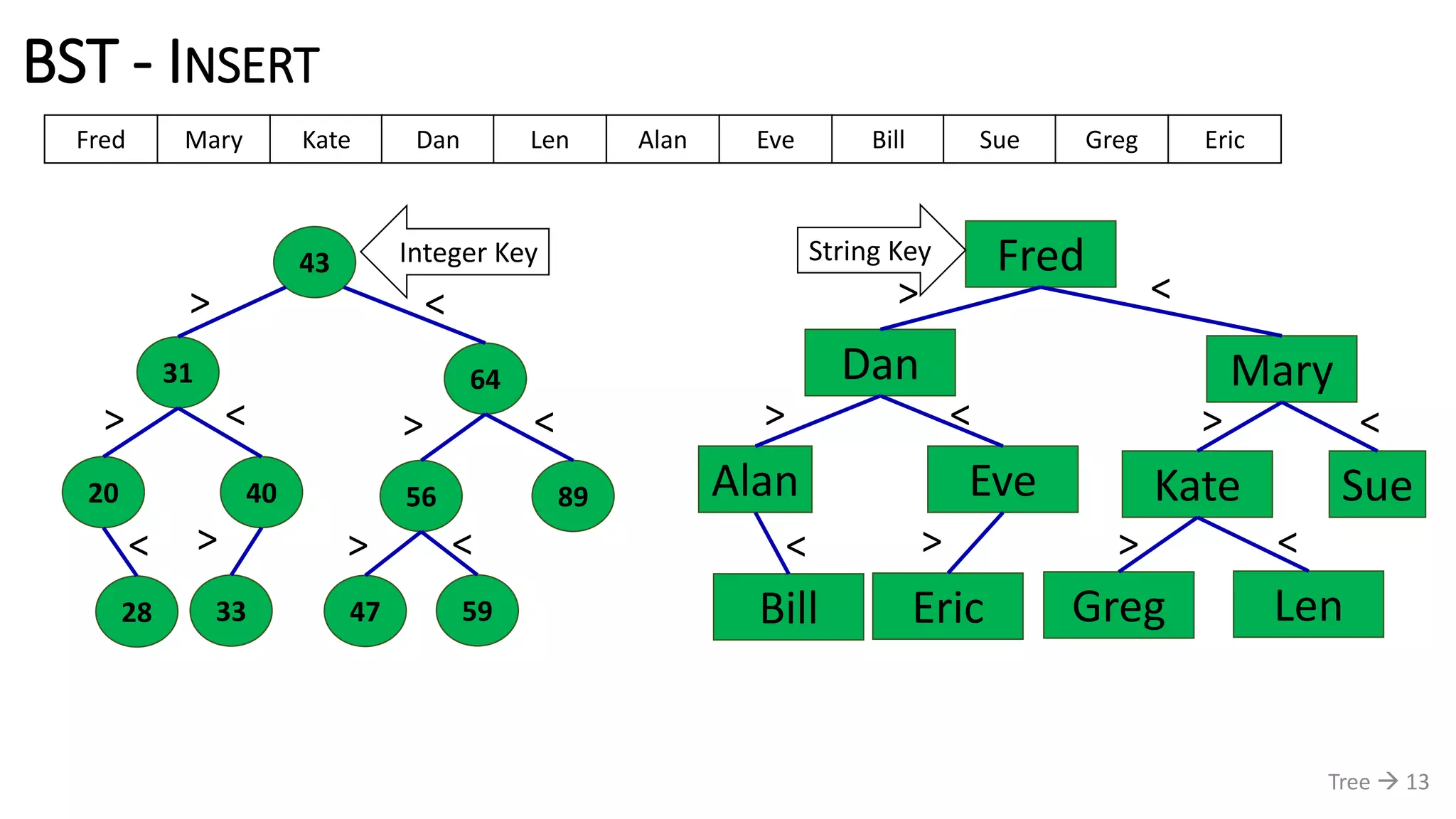
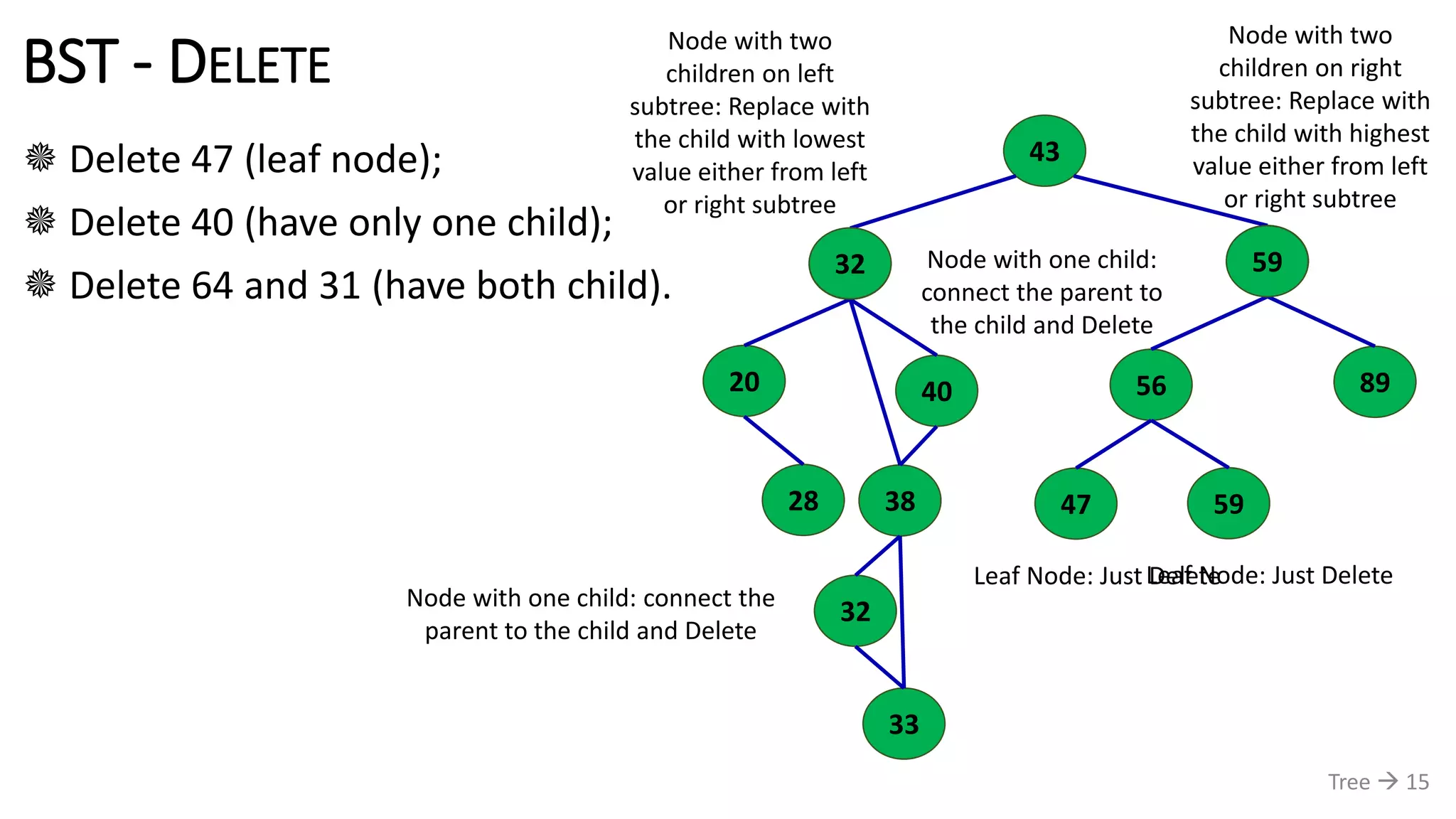
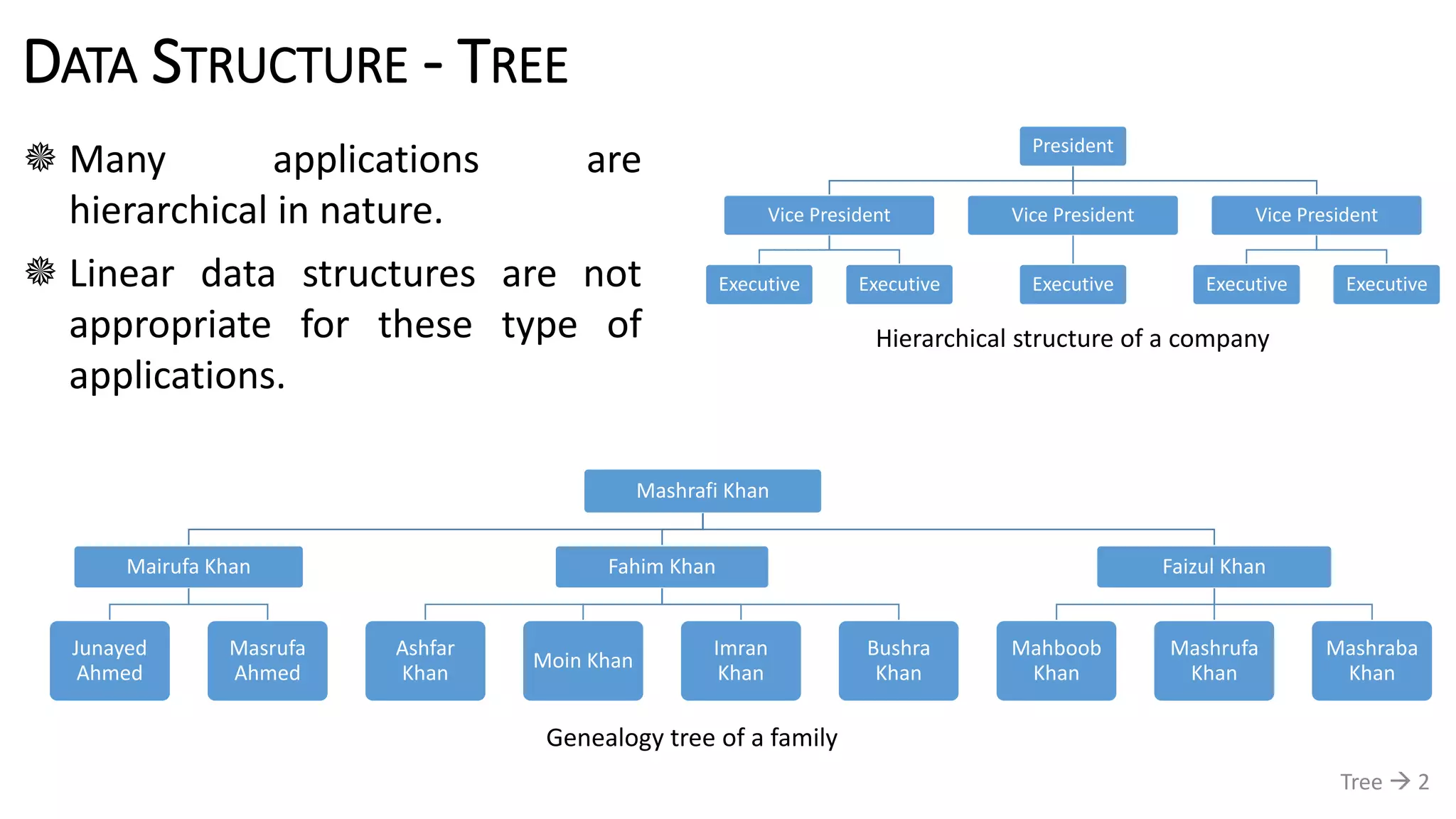
The document discusses tree data structures, emphasizing their hierarchical nature and various applications such as representing genealogies and workflows. It defines the characteristics of trees, including nodes, parent-child relationships, and traversal methods, detailing binary trees and binary search trees among others. Additionally, it outlines the concepts of complete and full binary trees, their construction, and operations like insertion, searching, and deletion.


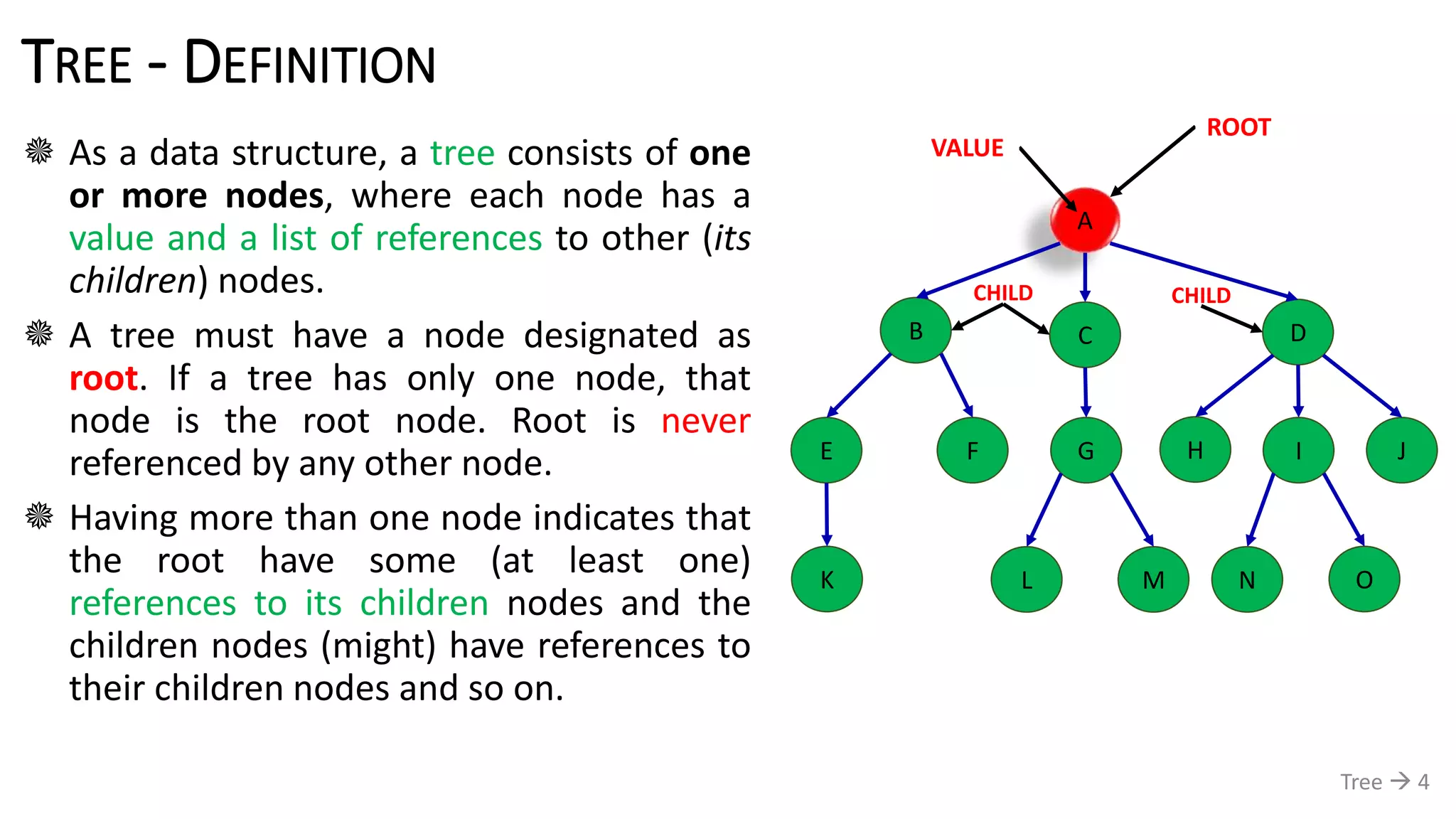
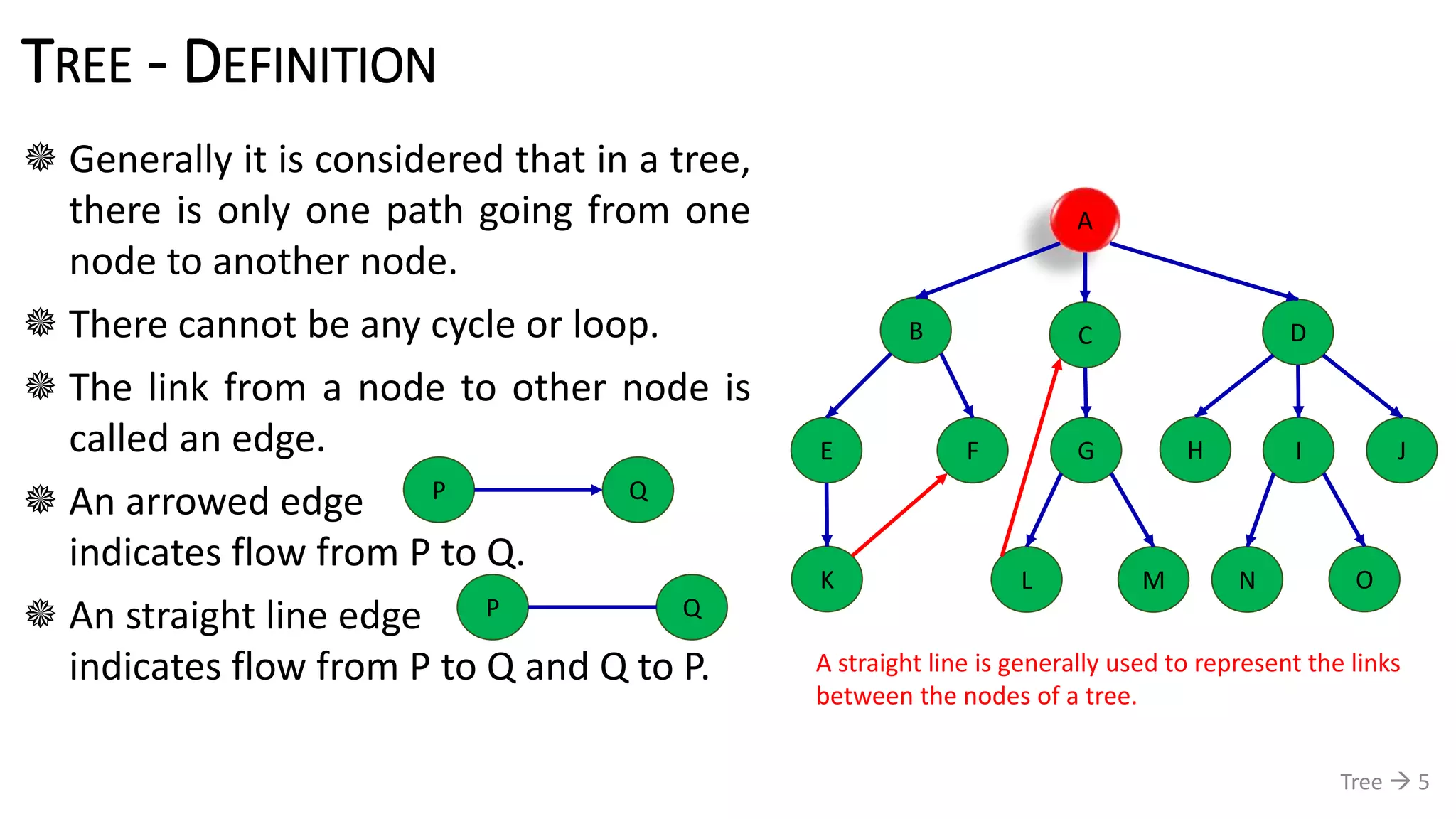
![TREE - DEFINITION
Nodes
Parent Nodes & Child Nodes
Leaf Nodes: nodes with no child
Root Node: node with no parent
Sub Tree: the tree rooted by a child
Level of a tree:
Root at level 0;
Each children have the level one more than
its parent.
Height/depth of the tree: Total
number of Levels
Height of a node: Total number of
levels from bottom
[Tree height – node level].
Tree 6
A
B C D
E F JIHG
K ML ON
LEVEL
0
1
2
3
Height of this tree is 4, as there are four levels (0…3).
Height of root A is 4;
Height of nodes B, C, D is 3;
Height of E, F, G, H, I, J is 2;
Height of nodes K, L , M, N, O is 1.](https://image.slidesharecdn.com/datastructuretree-intermediate-180728110246/75/Data-structure-tree-intermediate-6-2048.jpg)