Uploaded byShubhmay Potdar
Deep Dive into Hyperparameter Tuning
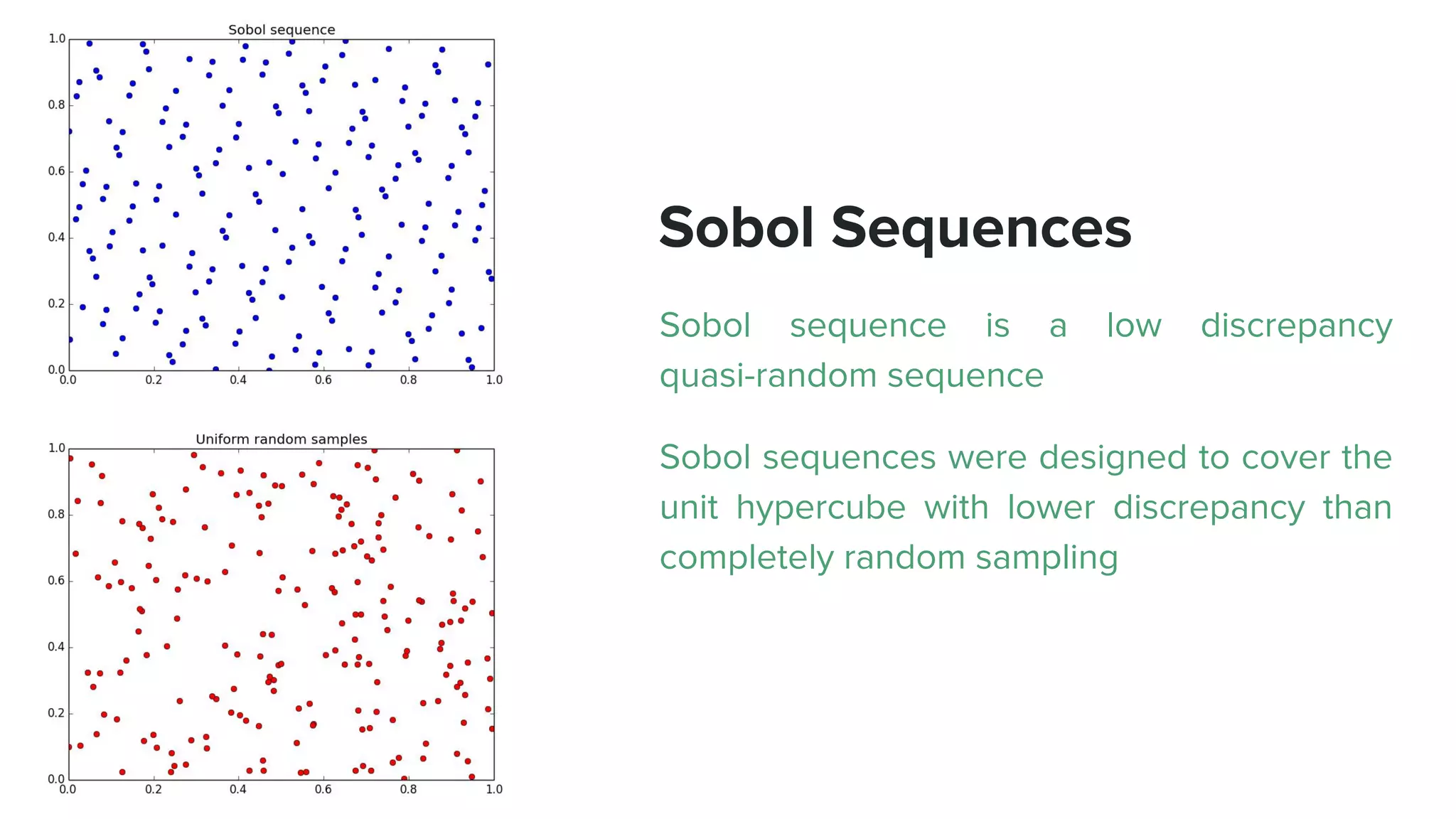
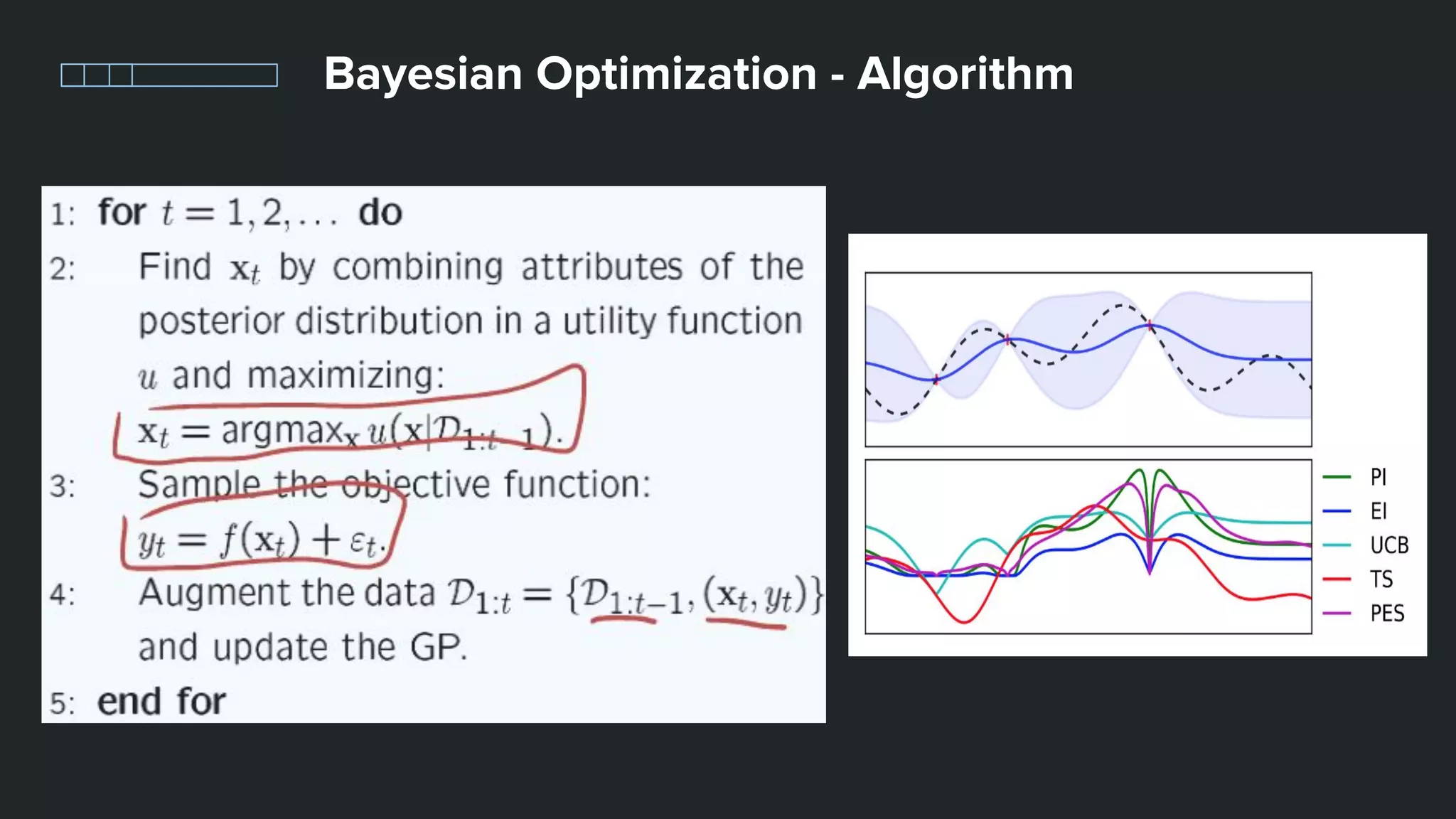
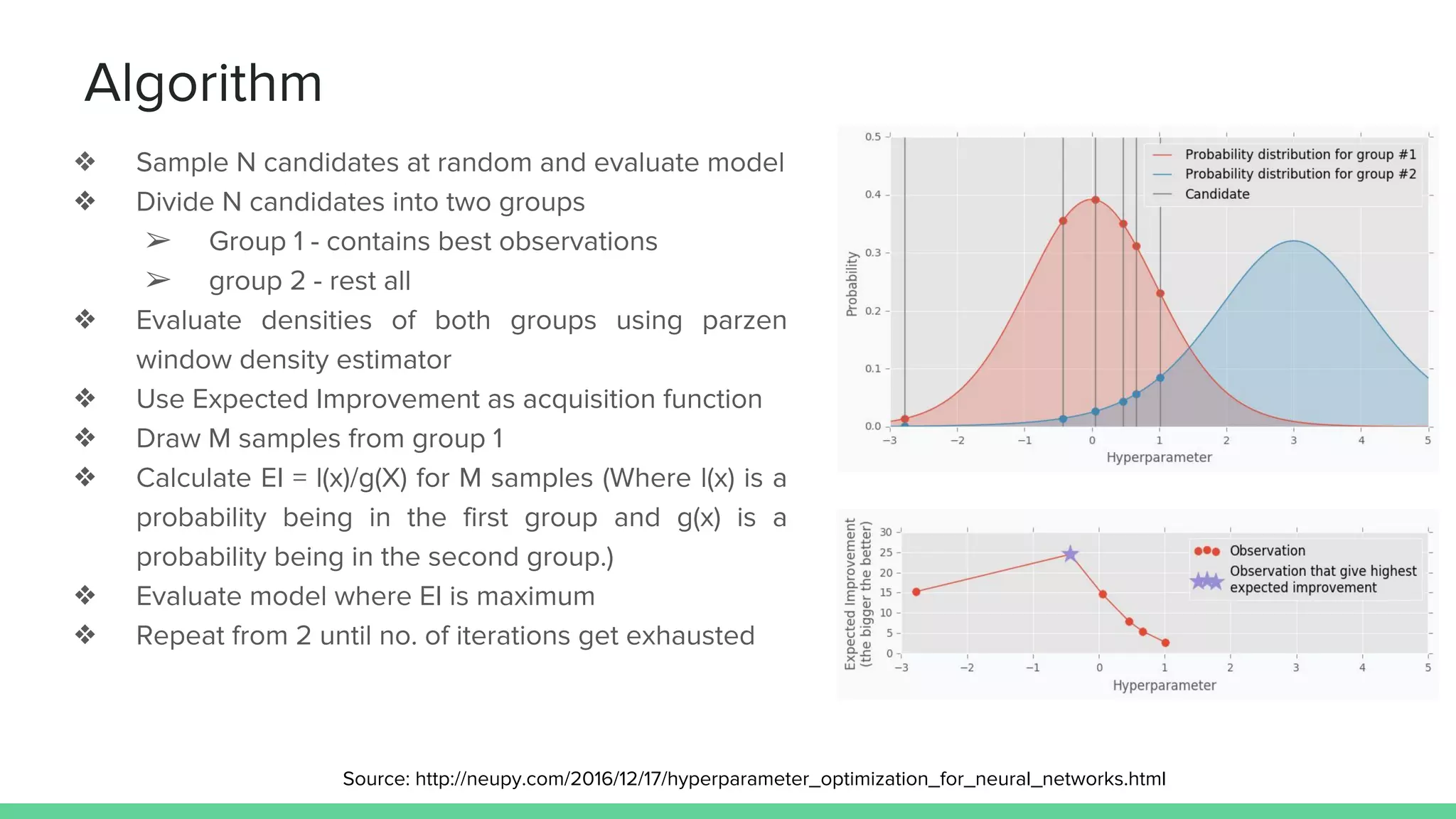
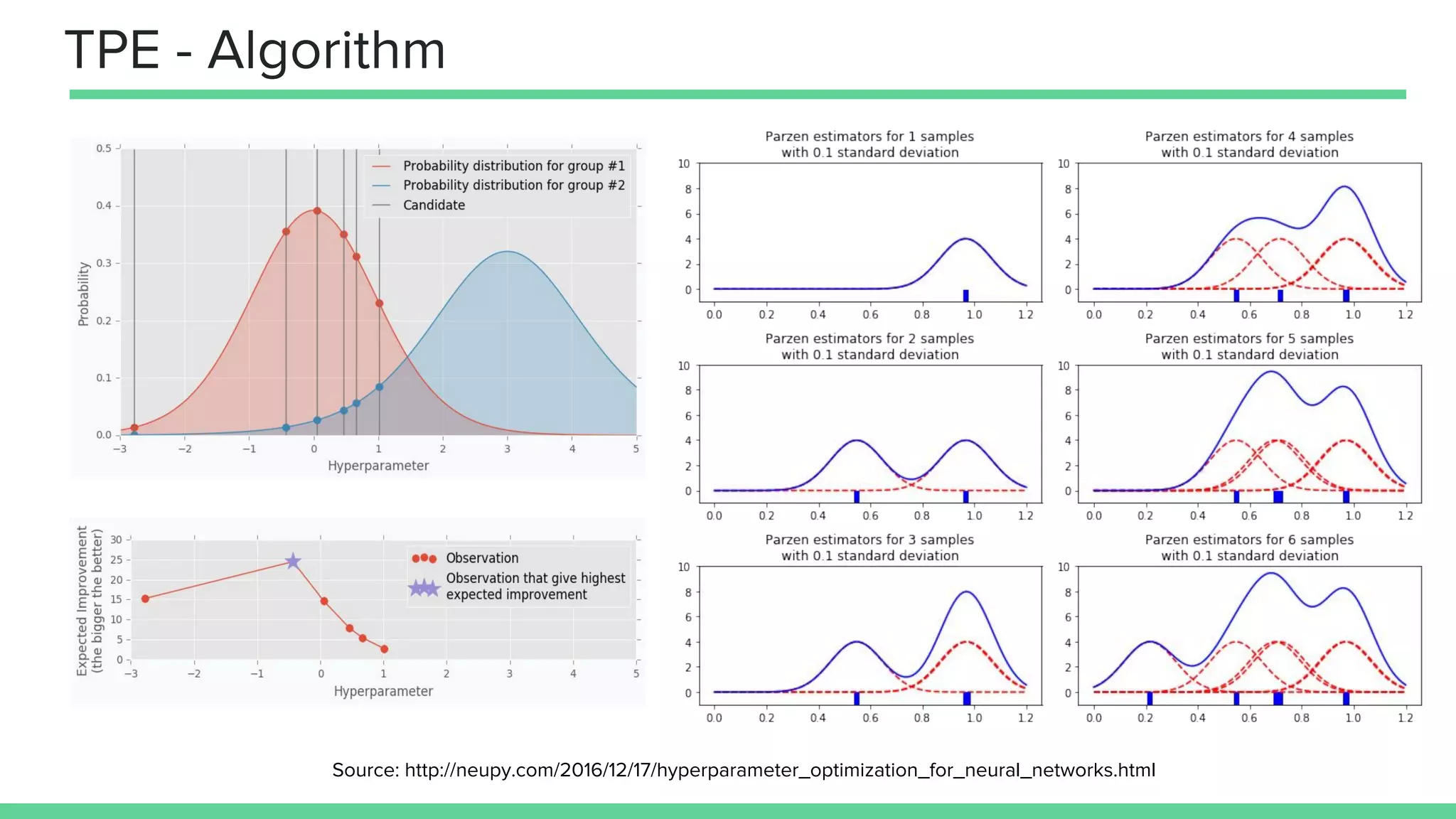
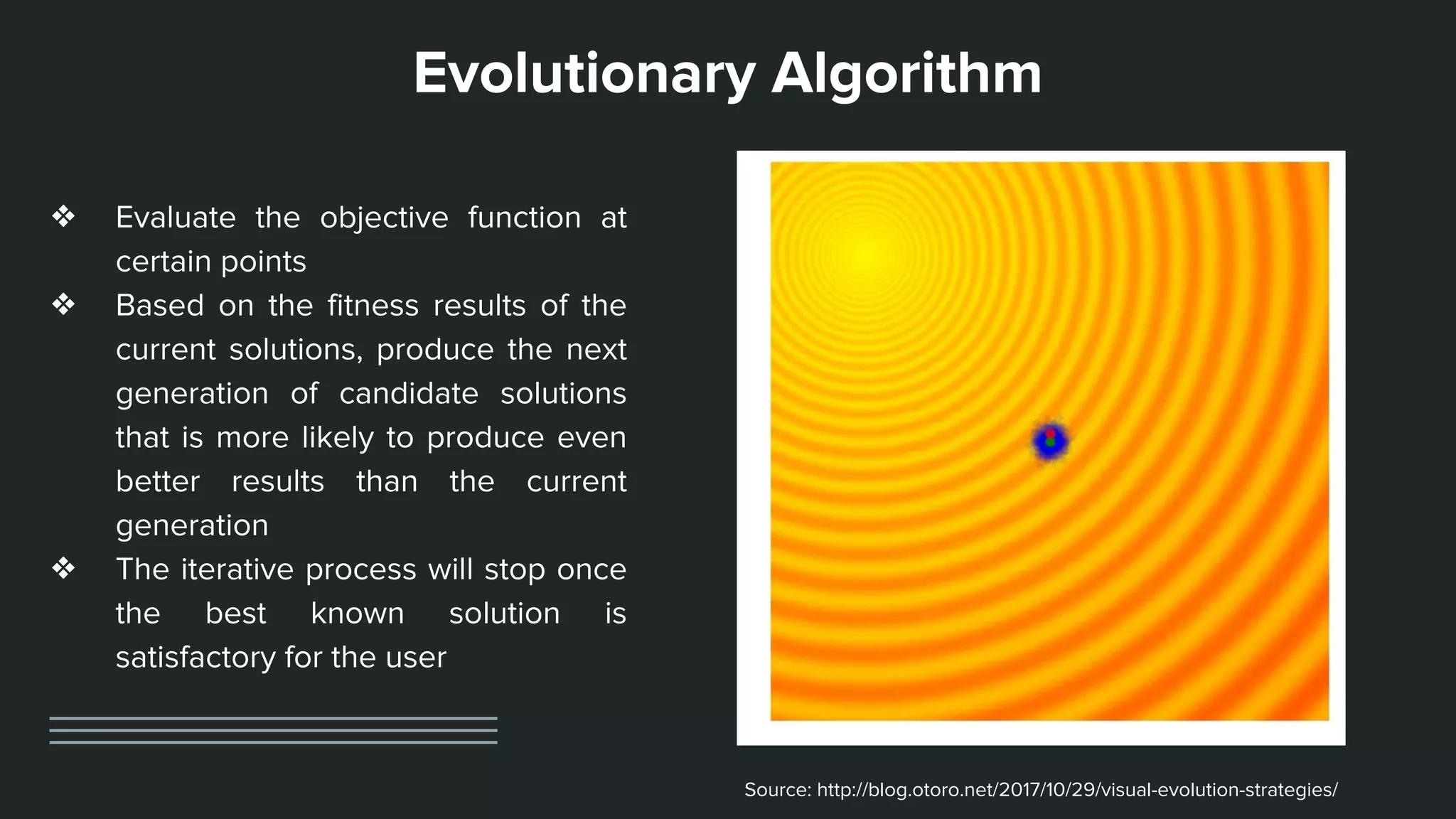
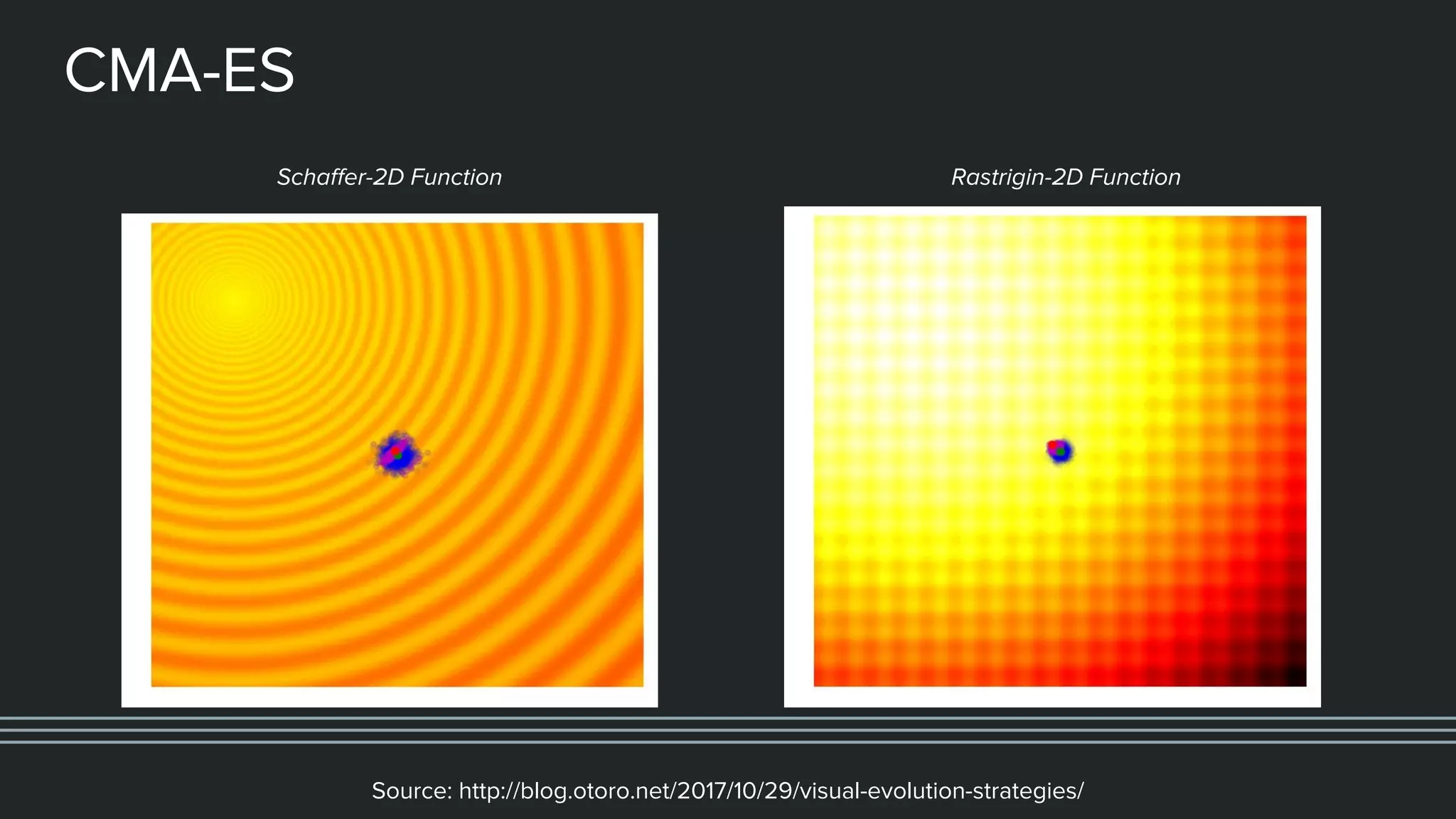
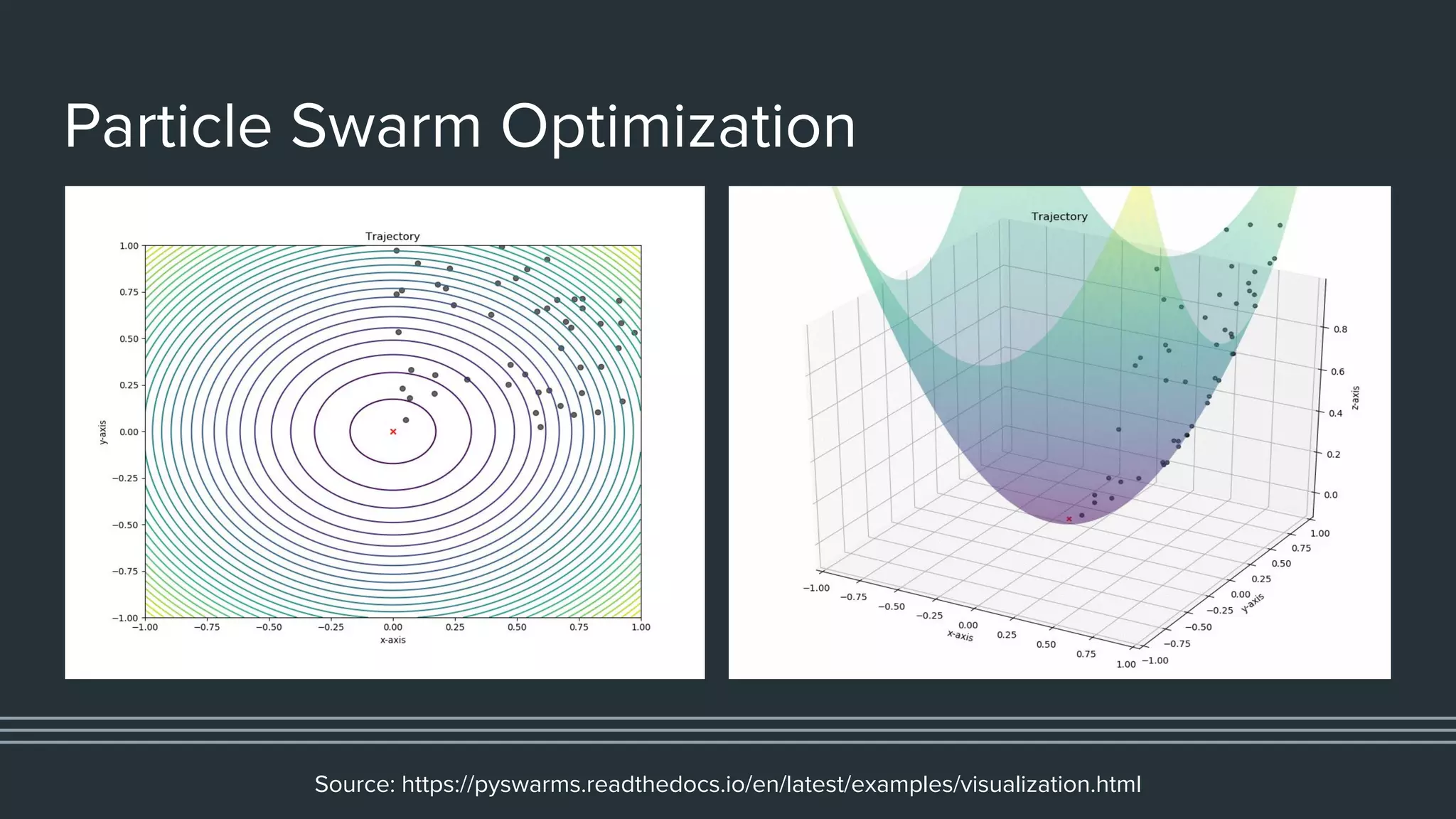
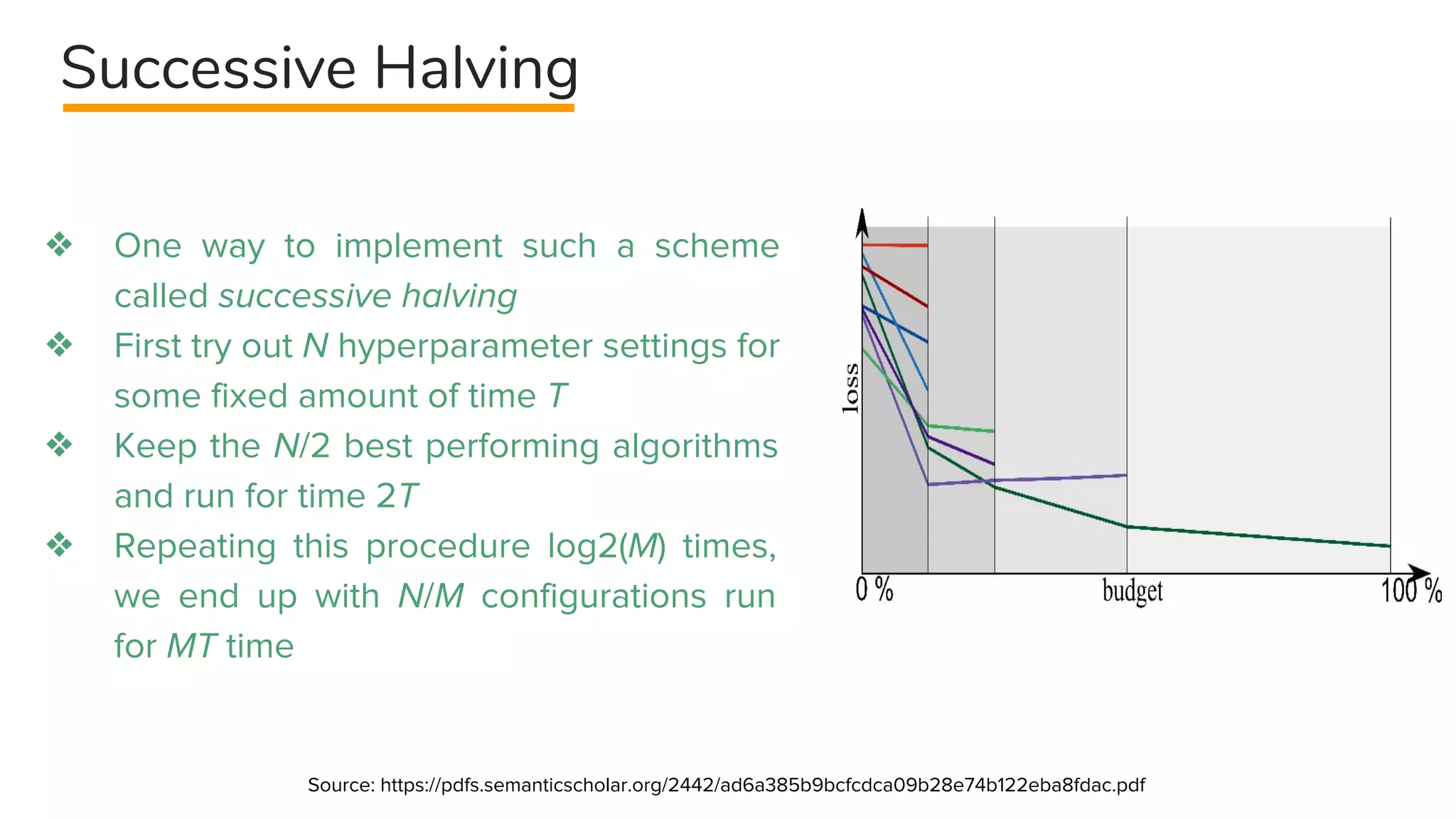
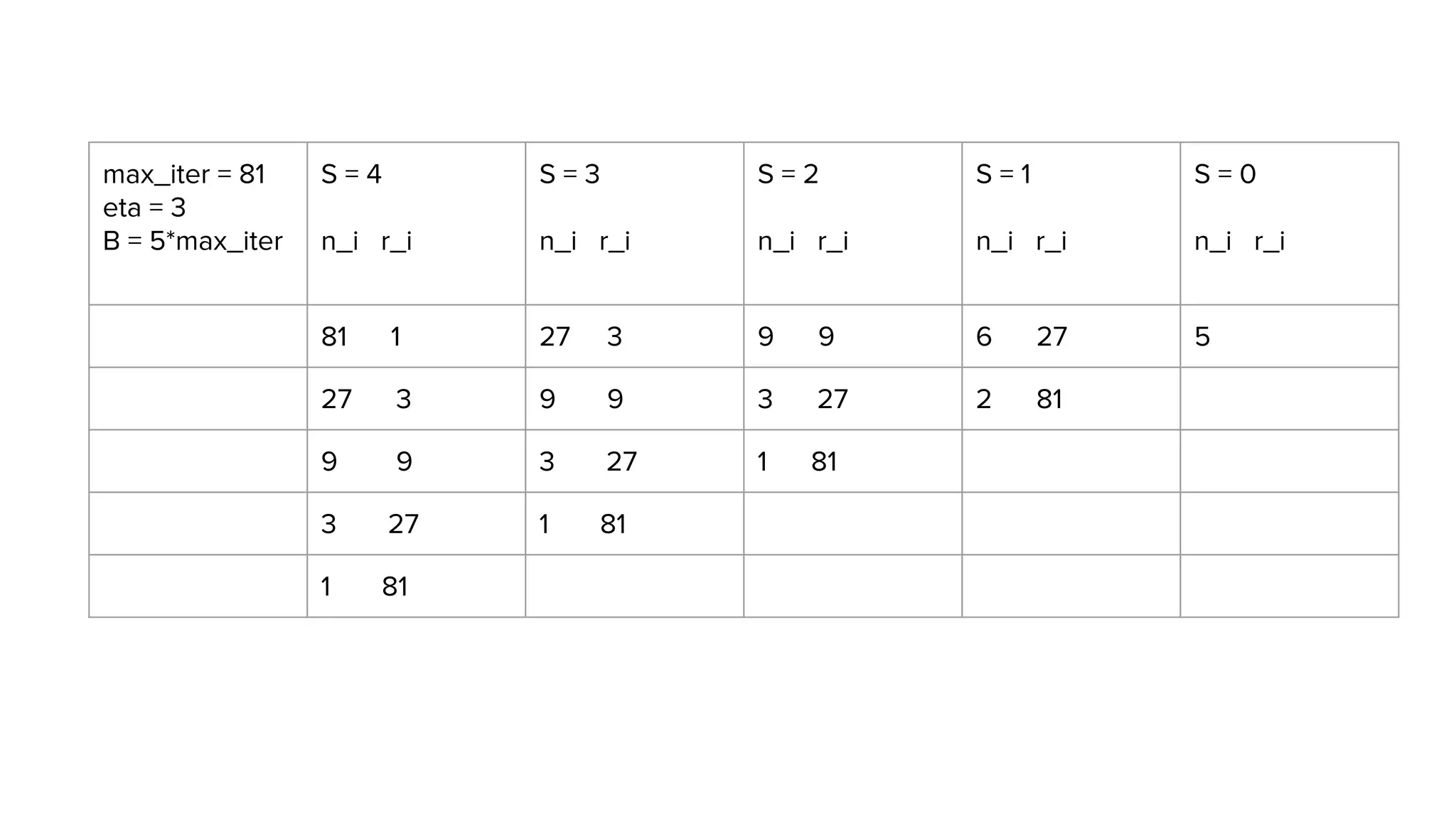
This document provides an overview of different techniques for hyperparameter tuning in machine learning models. It begins with introductions to grid search and random search, then discusses sequential model-based optimization techniques like Bayesian optimization and Tree-of-Parzen Estimators. Evolutionary algorithms like CMA-ES and particle-based methods like particle swarm optimization are also covered. Multi-fidelity methods like successive halving and Hyperband are described, along with recommendations on when to use different techniques. The document concludes by listing several popular libraries for hyperparameter tuning.
More Related Content
Similar to Deep Dive into Hyperparameter Tuning
![RTP_AR_Basic_Learners' Workbook_KS2 [FOR REPRODUCTION] (1).pdf](https://cdn.slidesharecdn.com/ss_thumbnails/rtparbasiclearnersworkbookks2forreproduction1-251016024943-e51a16ac-thumbnail.jpg?width=600ounds&width=560&fit=bounds)
Deep Dive into Hyperparameter Tuning
- 1.
- 2. About Me Shubhmay Potdar Sr.Software Engineer @ eQ-Technologic
- 3. Contents 1. Introduction toHyperparameter Tuning 2. Grid and Random Search 3. Sobol Sequences 4. Introduction to Sequential based Model Optimization a. Bayesian Optimization b. Tree of Parzen Estimator 5. Evolutionary Algorithms: CMA-ES 6. Particle Based Methods: Particle Swarm Optimization 7. Multi Fidelity Methods: Successive Halving and HyperBand 8. Libraries and Services for Hyperparameter Tuning 9. Future Scope for Research
- 4. Hyperparameters What are hyperparameters? In machine learning, a hyperparameters are set of configurations that are being assigned to the learning algorithm and whose values cannot be estimated using data. 1. Depth of tree ( Decision Tree) 2. No. of trees (Random Forest) 3. Regularization Parameters (XGBoost) 4. No. of layers (Deep Neural Network) Why are they required ? Good combinations are likely to give the best results Define complexity, ability to learn, structure of the model. Choosing correct values will help to eliminate the chances of overfitting and underfitting.
- 5. Exploration Problem Hyperparameter tuning canbe seen as an exploration problem The true structure of the underlying function is unknown Aim is to explore as many region as possible within some constraints
- 6. 1 2 34 Four Steps in Hyperparam Tuning Objective Function: what we want to minimize, in this case the validation error of a machine learning model with respect to the hyperparameters Domain Space: hyperparameter values to search over Optimization algorithm: method for constructing the surrogate model and choosing the next hyperparameter values to evaluate Result history: stored outcomes from evaluations of the objective function consisting of the hyperparameters and validation loss
- 7. Grid Search ❖ Selectvalues for each hyperparameter to test and try all combinations ❖ Expensive to evaluate all combinations Bergstra, James and Yoshua Bengio. “Random Search for Hyper-Parameter Optimization.” Journal of Machine Learning Research 13 (2012): 281-305.
- 8. Random Search ❖ Selectvalues randomly for every hyperparameter ❖ Evaluations are independent, can be evaluated parallely ❖ Specify distribution of parameters for effective sampling Bergstra, James and Yoshua Bengio. “Random Search for Hyper-Parameter Optimization.” Journal of Machine Learning Research 13 (2012): 281-305.
- 9. Sobol Sequences Sobol sequenceis a low discrepancy quasi-random sequence Sobol sequences were designed to cover the unit hypercube with lower discrepancy than completely random sampling
- 10. Preview SMBO Canwe do better than grid and random search ? Can we have a guided tour in our journey for finding optimal parameters ? We know that the cost of evaluation of our training algorithm is significantly large in most cases And obviously we are not guaranteed that the given set of parameters will give the optimal solution https://pixabay.com/en/light-bulb-ideas-sketch-i-think-487859/
- 11. Bayesian Optimization Bayesian optimization isa framework that is useful in following scenarios: ❖ Objective function has no closed-form ❖ No access to gradients ❖ In presence of noise ❖ It may be expensive to evaluate.
- 12. Bayesian Optimization -Main Components Surrogate Function: Needed to approximate the objective function and chooses to optimize it according to some acquisition function Common choices are Gaussian Process, Random Forest, Gradient Boosted Machines Acquisition function: Helps to select next point for evaluation Trade off between exploring unknown regions versus exploiting known regions Common choices are Expected Improvement, Upper Confidence Bound, Probability of Improvement, Thompson Sampling etc.
- 13. Bayesian Optimization -Algorithm
- 14.
- 15. Expected Improvement f∗ -current optimal value Quantify the improvement over f∗ if we sample a point x - I(x) = max(f∗ − Y, 0) If f is modelled using GP, where ϕ,Φ are the PDF, CDF of standard normal distribution, respectively
- 16. Challenges How to designsurrogate function that models the objective function and which is also cheap to evaluate How to design the helper function that guarantee tradeoff between exploration and exploitation https://pixabay.com/en/overcoming-stone-roll-slide-strong-2127669/
- 17. Drawbacks ❖ Complexity ofGP is O(n^3) ❖ Hyperparameters for GP itself ❖ Difficult to parallelize ❖ Can stuck at local minima
- 18. Tree of Parzen Estimator Wetend to explore more in the region where we got high percentage of optimal values in our exploration.
- 19. Algorithm ❖ Sample Ncandidates at random and evaluate model ❖ Divide N candidates into two groups ➢ Group 1 - contains best observations ➢ group 2 - rest all ❖ Evaluate densities of both groups using parzen window density estimator ❖ Use Expected Improvement as acquisition function ❖ Draw M samples from group 1 ❖ Calculate EI = l(x)/g(X) for M samples (Where l(x) is a probability being in the first group and g(x) is a probability being in the second group.) ❖ Evaluate model where EI is maximum ❖ Repeat from 2 until no. of iterations get exhausted Source: http://neupy.com/2016/12/17/hyperparameter_optimization_for_neural_networks.html
- 20. TPE - Algorithm Source:http://neupy.com/2016/12/17/hyperparameter_optimization_for_neural_networks.html
- 21. Evolutionary Algorithm ❖ Evaluatethe objective function at certain points ❖ Based on the fitness results of the current solutions, produce the next generation of candidate solutions that is more likely to produce even better results than the current generation ❖ The iterative process will stop once the best known solution is satisfactory for the user Source: http://blog.otoro.net/2017/10/29/visual-evolution-strategies/
- 22. Algorithm 1. Startwith N candidates 2. Calculate the fitness score of each candidate solution 3. Isolates the best 25% of the population in generation 4. Using only the best solutions, along with the mean μ(g) of the current generation 5. Calculate the covariance matrix C(g+1) of the next generation 6. Sample a new set of candidate solutions using the updated mean μ(g+1) and covariance matrix C(g+1)
- 23. CMA-ES Schaffer-2D Function Rastrigin-2DFunction Source: http://blog.otoro.net/2017/10/29/visual-evolution-strategies/
- 24. Particle Swarm Optimization ❖heuristic optimization technique ❖ simulates a set of particles that are moving around in the search space ❖ for hyperparameter search, position of a particle represents a set of hyperparameters and its movement is influenced by the goodness of the objective function value
- 25.
- 26. Particle Swarm Optimization Source:https://pyswarms.readthedocs.io/en/latest/examples/visualization.html
- 27. Multi-Fidelity Optimization ❖ Idea isto be replace full evaluation with cheap approproximations ➢ using subset of data ➢ cross validations on few folds ➢ few iteration of algorithm ❖ Reject significantly worst performing configuration
- 28. Hyperband ❖ Employspure exploration approach ❖ The idea is to try a large number of random configurations ❖ By computing more efficiently, it tries at more hyperparameter configurations ❖ Most of the algorithms are iterative in machine learning, ❖ If we are running a set of parameters, and the progress looks terrible, it might be a good idea to quit and just try a new set of hyperparameters
- 29. Successive Halving ❖ Oneway to implement such a scheme called successive halving ❖ First try out N hyperparameter settings for some fixed amount of time T ❖ Keep the N/2 best performing algorithms and run for time 2T ❖ Repeating this procedure log2(M) times, we end up with N/M configurations run for MT time Source: https://pdfs.semanticscholar.org/2442/ad6a385b9bcfcdca09b28e74b122eba8fdac.pdf
- 30. max_iter = 81 eta= 3 B = 5*max_iter S = 4 n_i r_i S = 3 n_i r_i S = 2 n_i r_i S = 1 n_i r_i S = 0 n_i r_i 81 1 27 3 9 9 6 27 5 27 3 9 9 3 27 2 81 9 9 3 27 1 81 3 27 1 81 1 81
- 31. Suggestions If allhyperparameters are real-valued and one can only afford a few dozen function evaluations, we recommend the use of a Gaussian process-based Bayesian optimization For large and conditional configuration spaces we suggest either the random forest-based SMAC or TPE due to their proven strong performance For purely real-valued spaces and relatively cheap objective functions, for which we can afford more than hundreds of evaluations,use CMA-ES
- 32. Library Optunity -https://optunity.readthedocs.io/en/latest/ Deap - https://github.com/DEAP/deap Smac3 - https://github.com/automl/SMAC3 Tune - https://ray.readthedocs.io/en/latest/tune.html GPyOpt - https://sheffieldml.github.io/GPyOpt/ Scikit-optimize - https://scikit-optimize.github.io/ Hyperopt - https://github.com/hyperopt/hyperopt Hyperband - https://github.com/zygmuntz/hyperband
- 33.