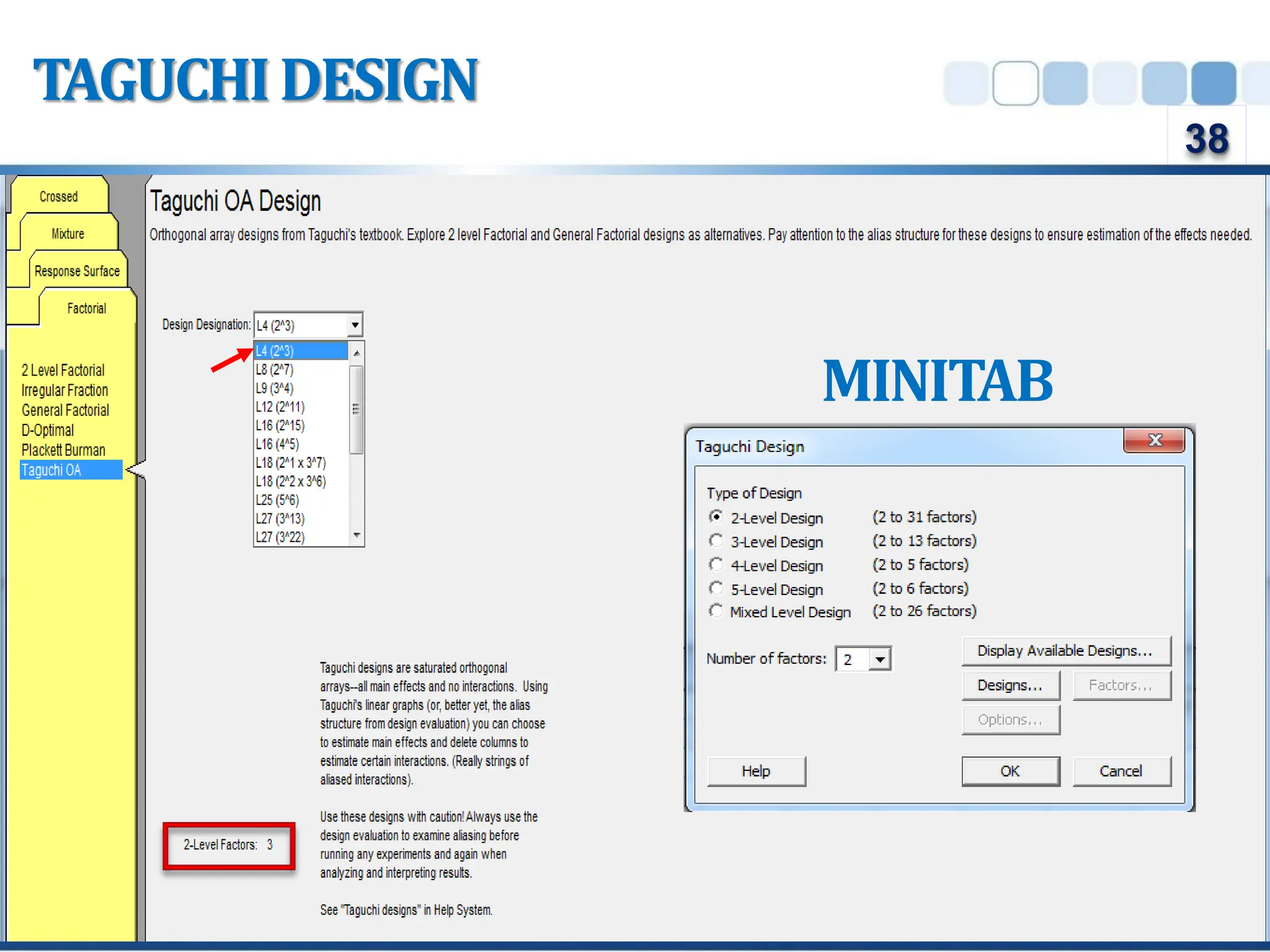
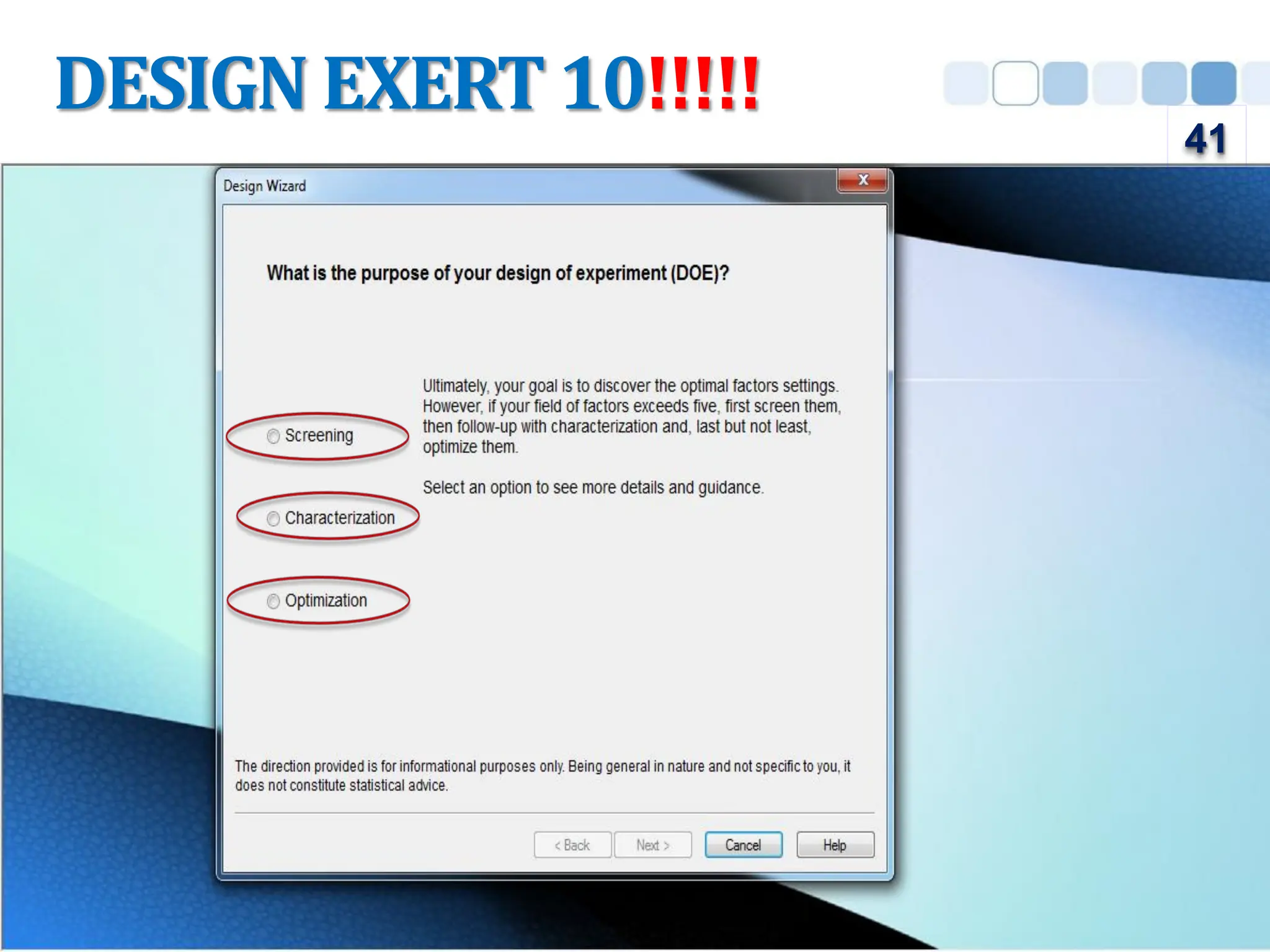
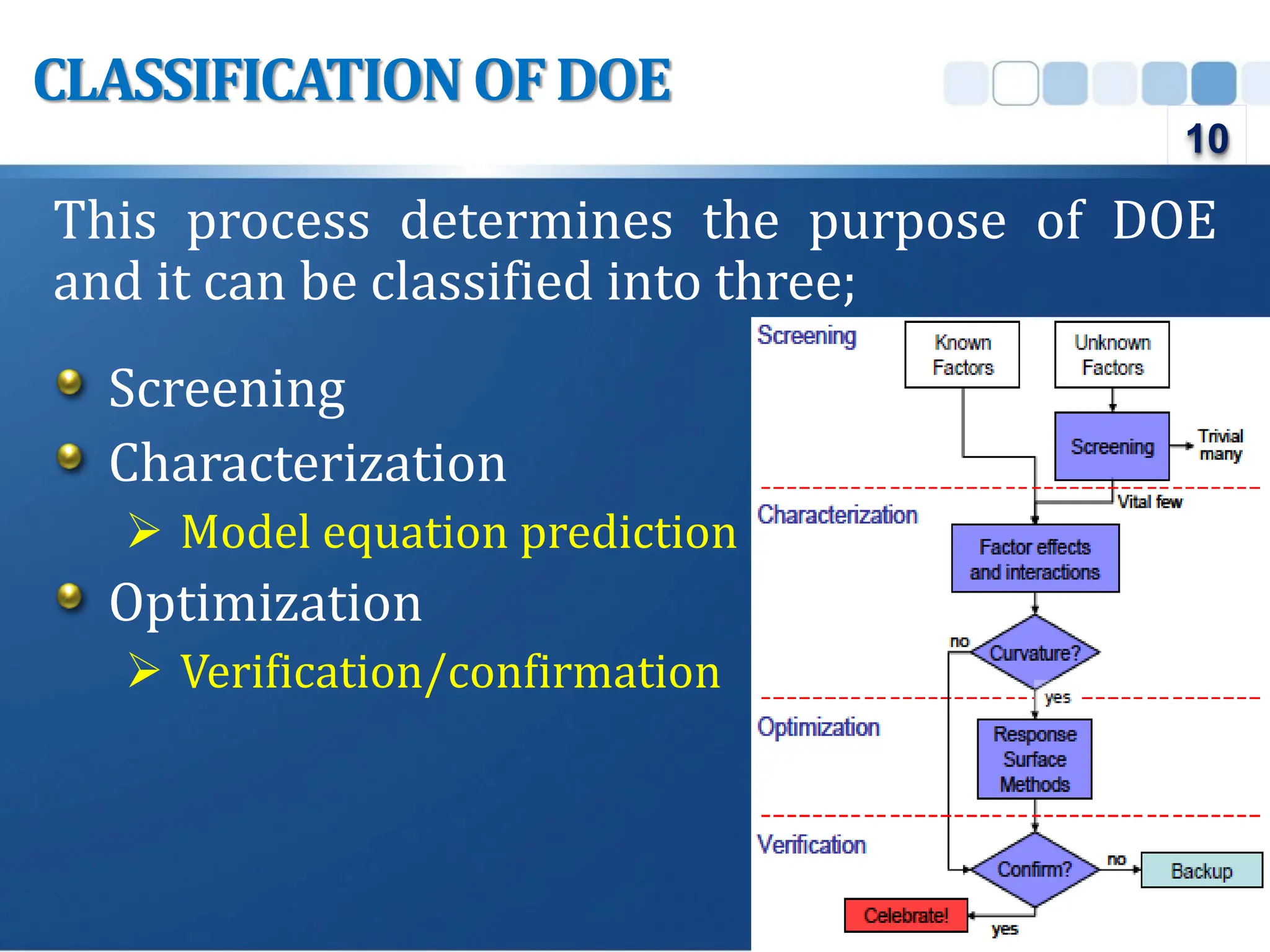
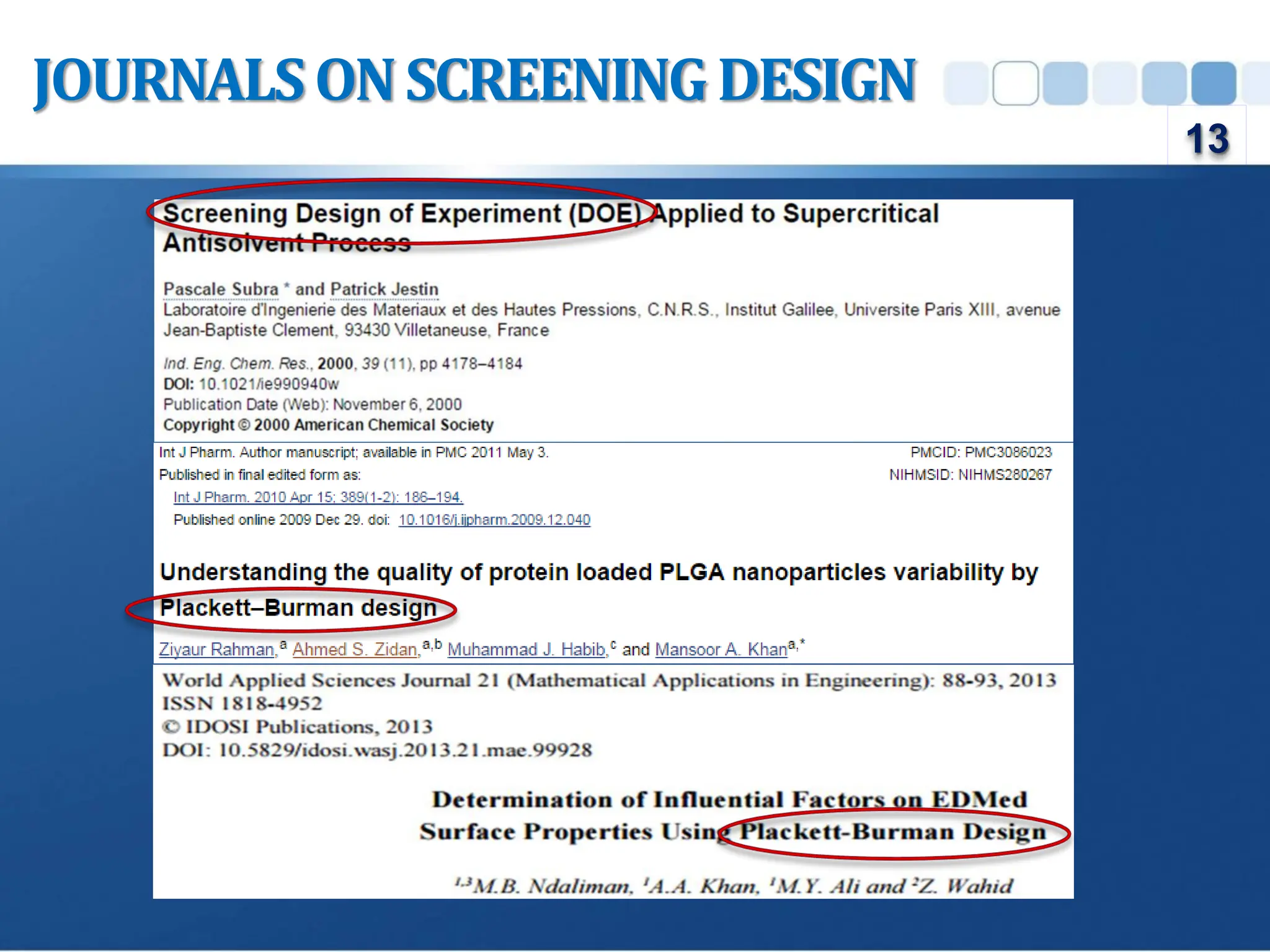
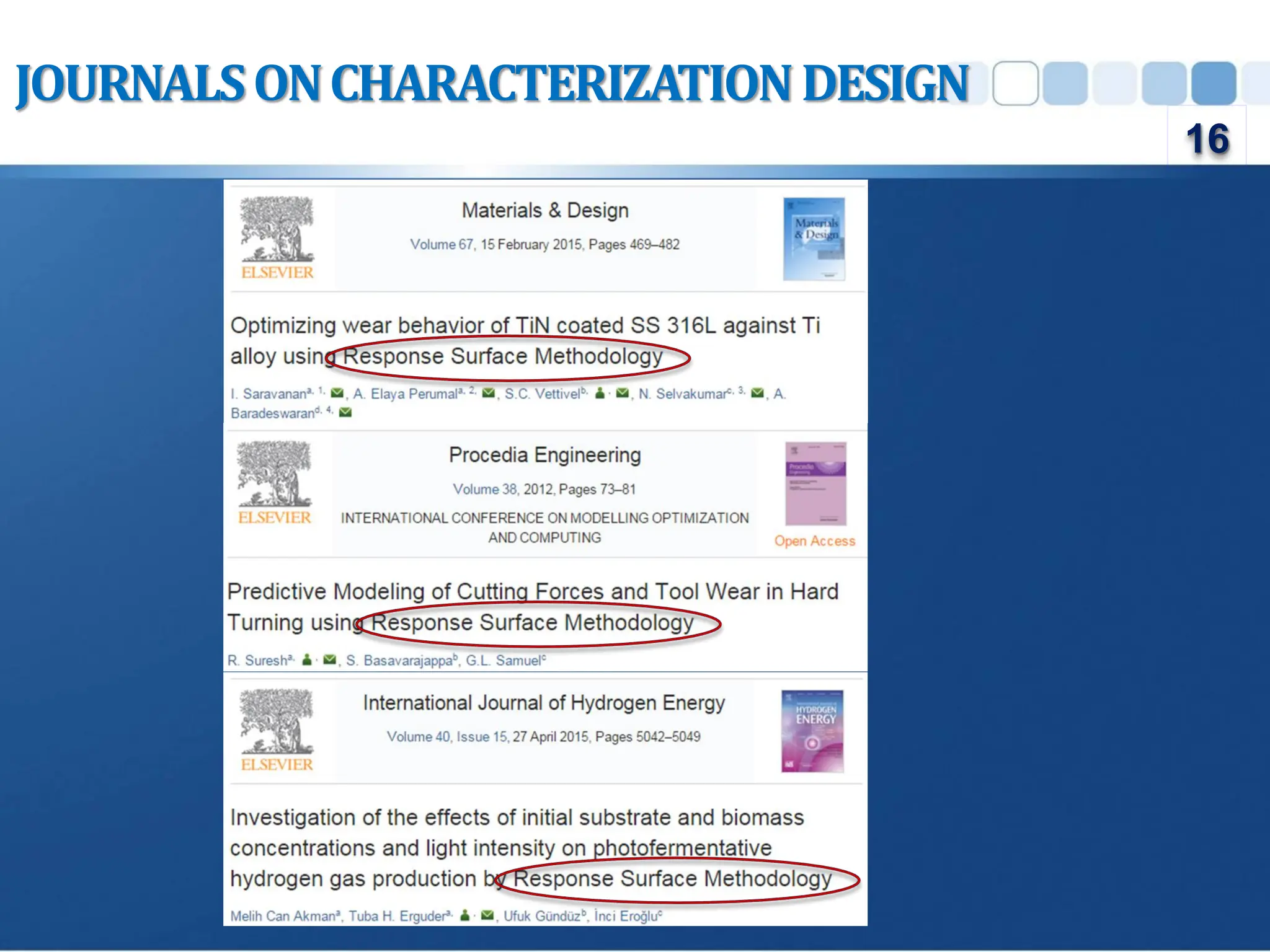
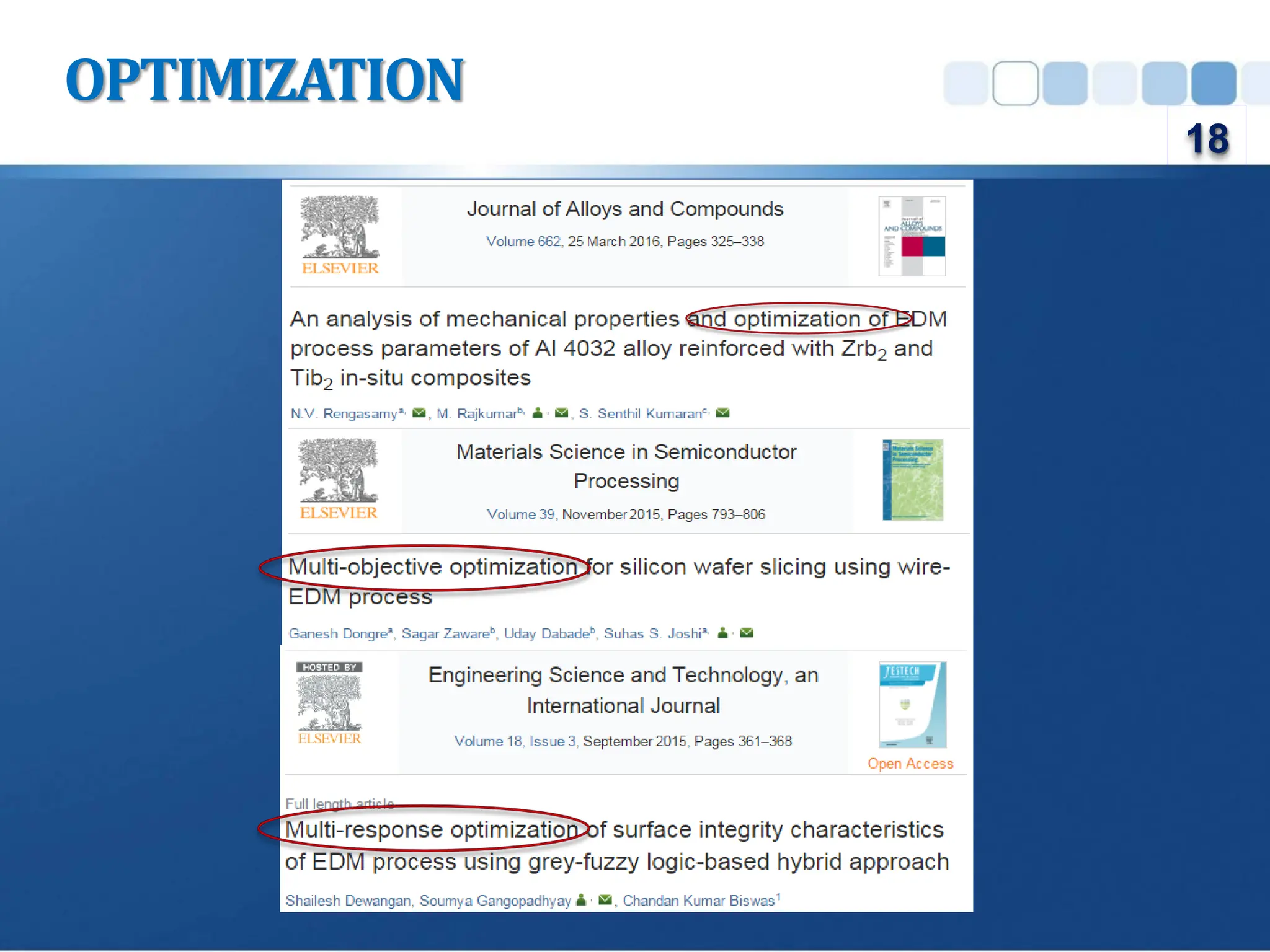
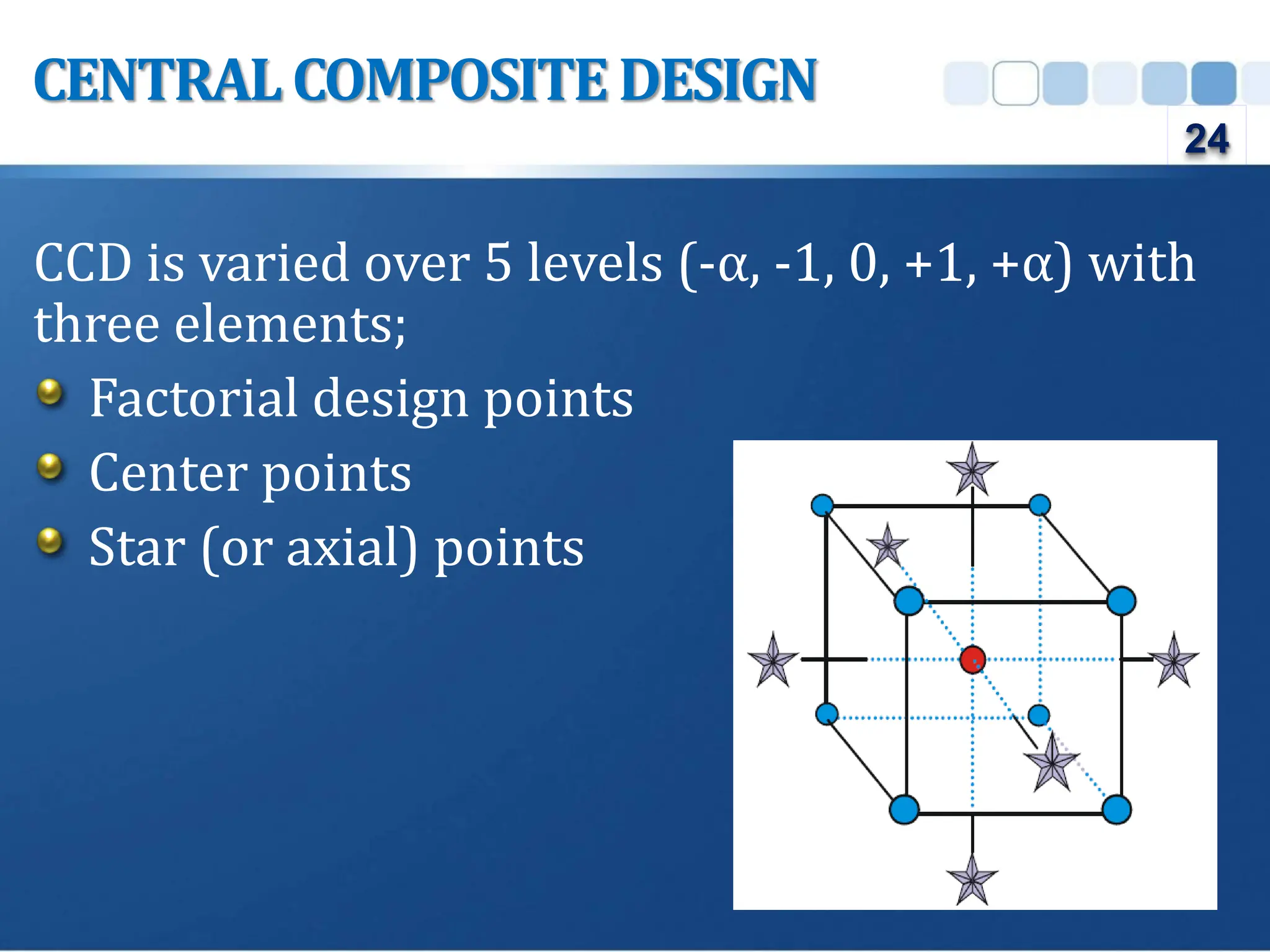
Design of Experiment (DOE) is a structured approach to conducting experiments to identify the relationships between input factors and output responses, aiding in cause-and-effect analysis. The document outlines various types of DOE, including screening, characterization, and optimization designs, and discusses their methodologies and applications. Key principles such as replication, randomization, and blocking are emphasized for obtaining reliable experimental conclusions.


















![Types of CCD
Circumscribed (CCC)
Faced centered (CCF)
Inscribed (CCI)
To maintain rotatability, the value of α
depends on the number of experimental
runs:
α=[number of factorial runs]1/4
If the factorial is a full factorial, then
α=[2k]1/4
CENTRALCOMPOSITE DESIGN
26](https://image.slidesharecdn.com/designofexperiment-240703100024-13b8a06f/75/Design-of-Experiment-for-Optimization-Analysis-24-2048.jpg)
![CENTRALCOMPOSITE DESIGN
α=[2k]1/4 where k = 2
Therefore α = 1.41421
Total number of runs = 2k + 2k + n
27](https://image.slidesharecdn.com/designofexperiment-240703100024-13b8a06f/75/Design-of-Experiment-for-Optimization-Analysis-25-2048.jpg)
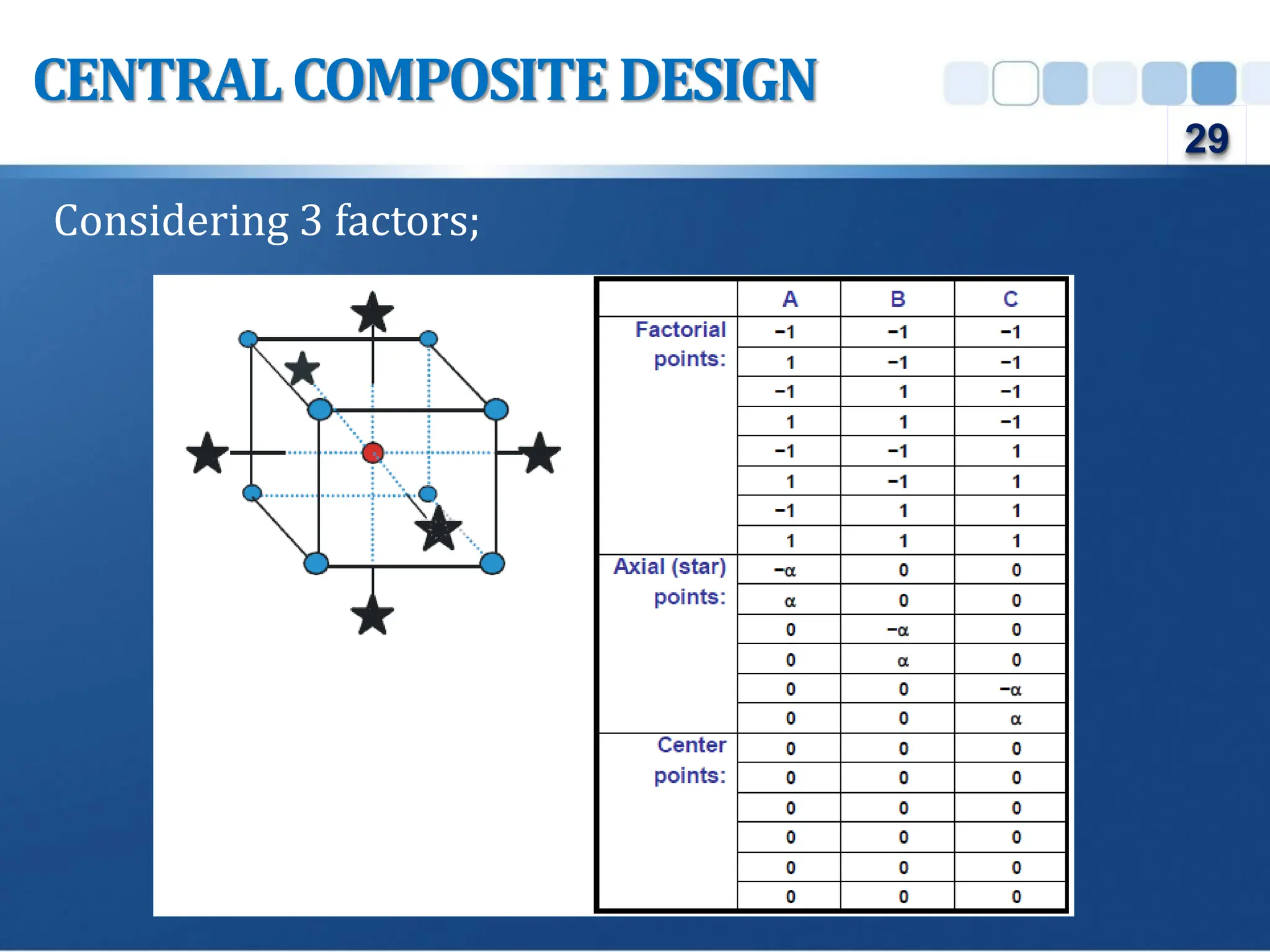
![CENTRALCOMPOSITE DESIGN
α=[2k]1/4 where k = 3
Therefore α = 1.68179
Total number of runs = 2k + 2k + n
28](https://image.slidesharecdn.com/designofexperiment-240703100024-13b8a06f/75/Design-of-Experiment-for-Optimization-Analysis-26-2048.jpg)
![CENTRALCOMPOSITE DESIGN
α=[2k]1/4 where k = 4
Therefore α = 2
Total number of runs = 2k + 2k + n
30](https://image.slidesharecdn.com/designofexperiment-240703100024-13b8a06f/75/Design-of-Experiment-for-Optimization-Analysis-28-2048.jpg)