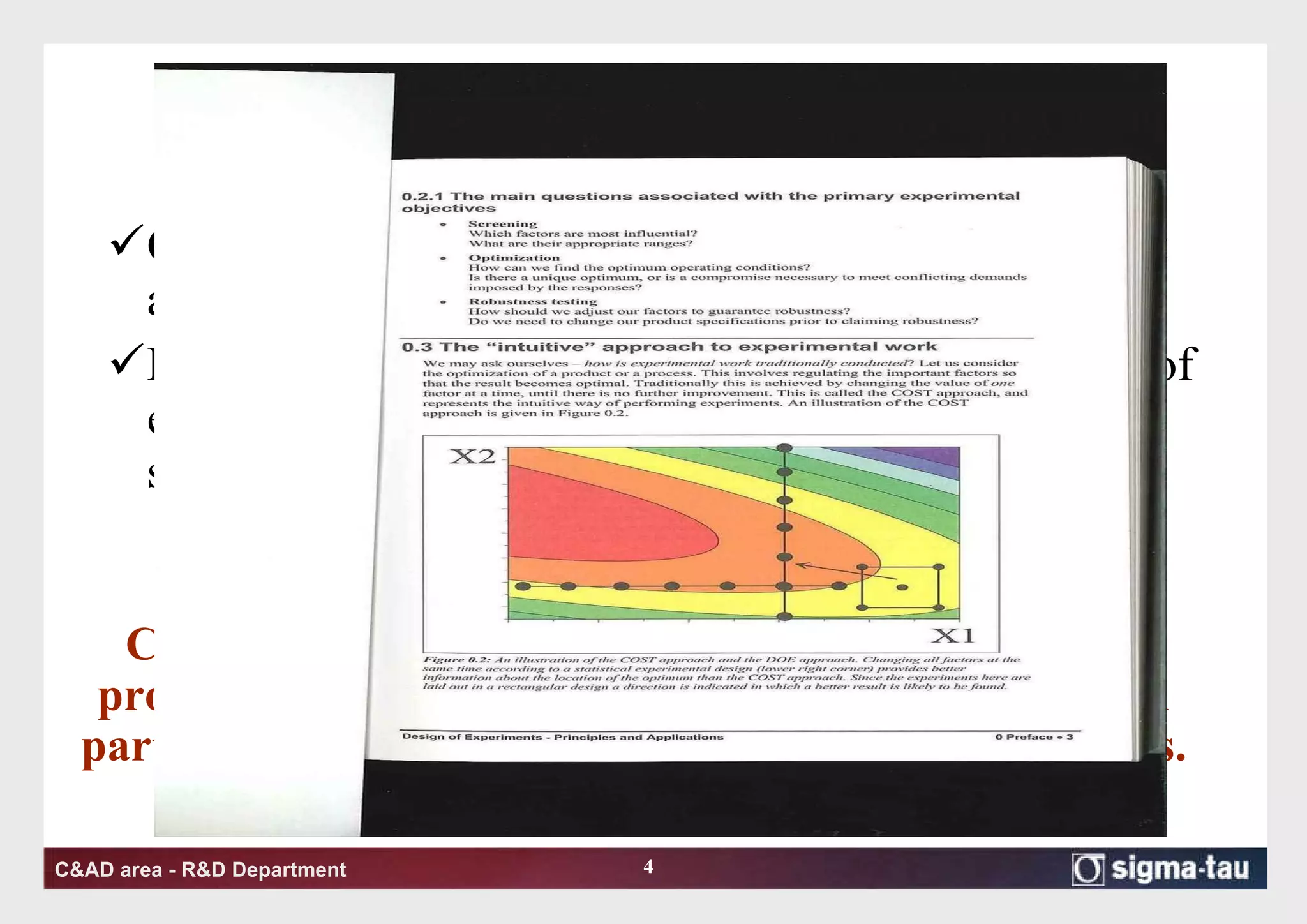
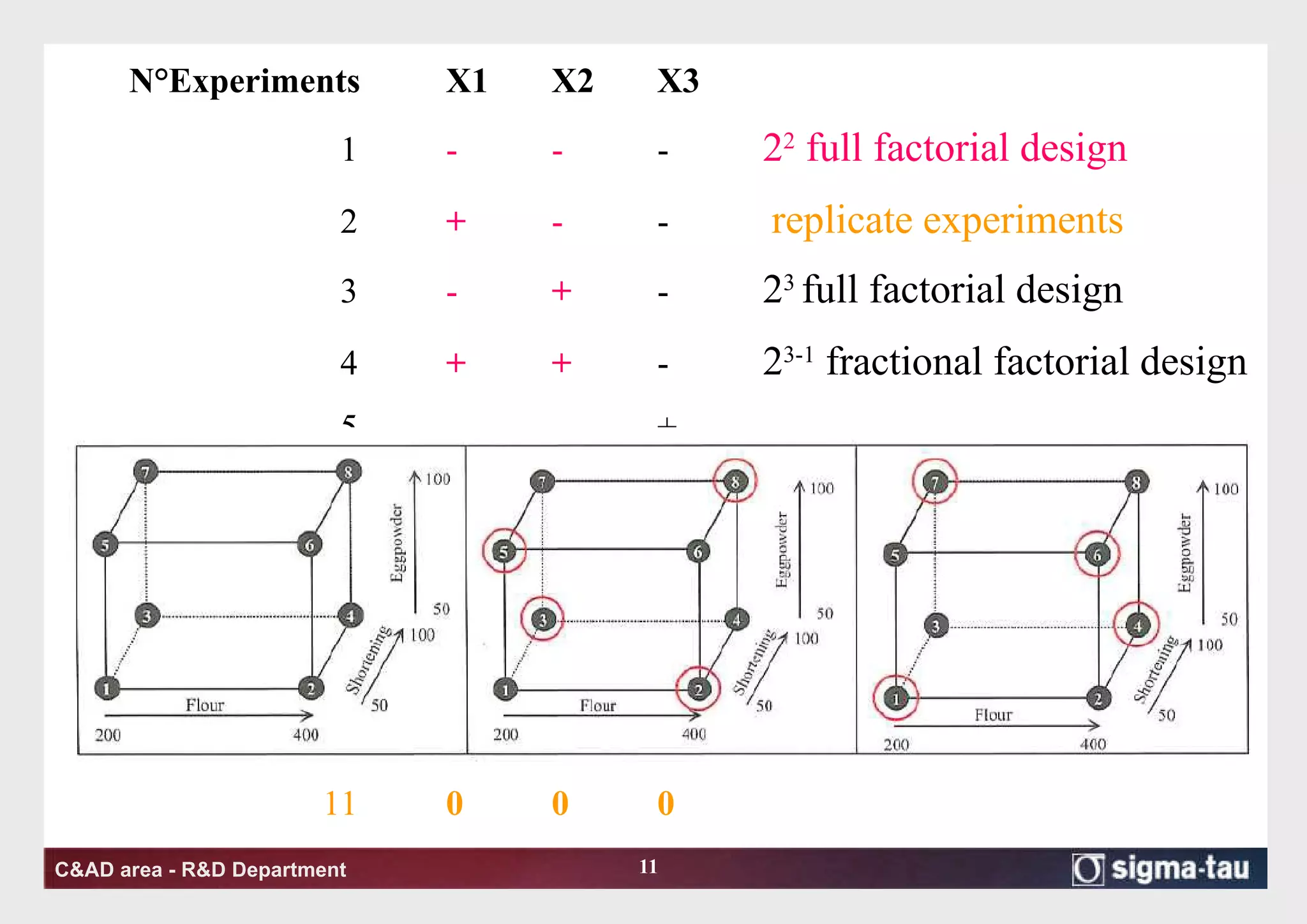
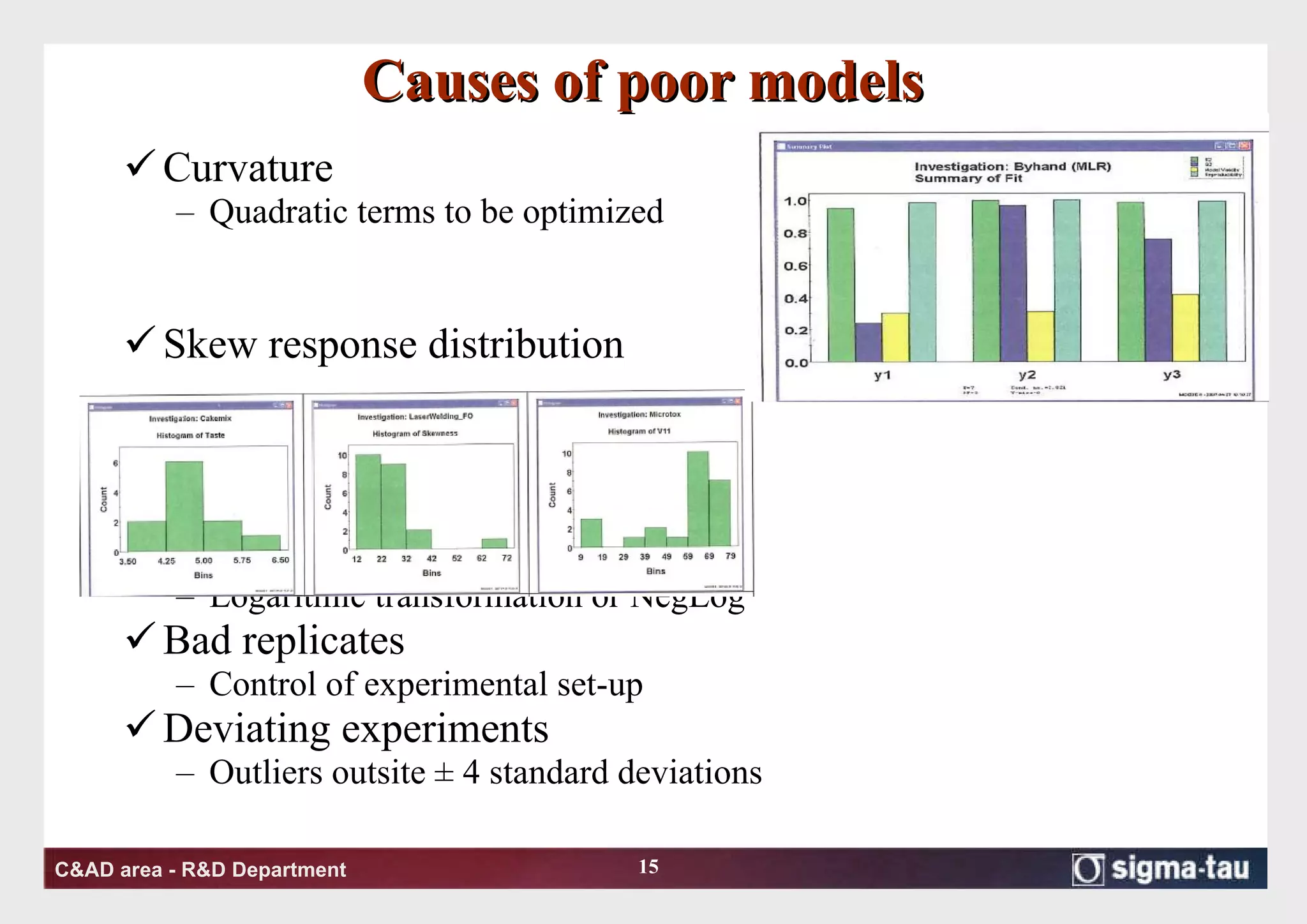
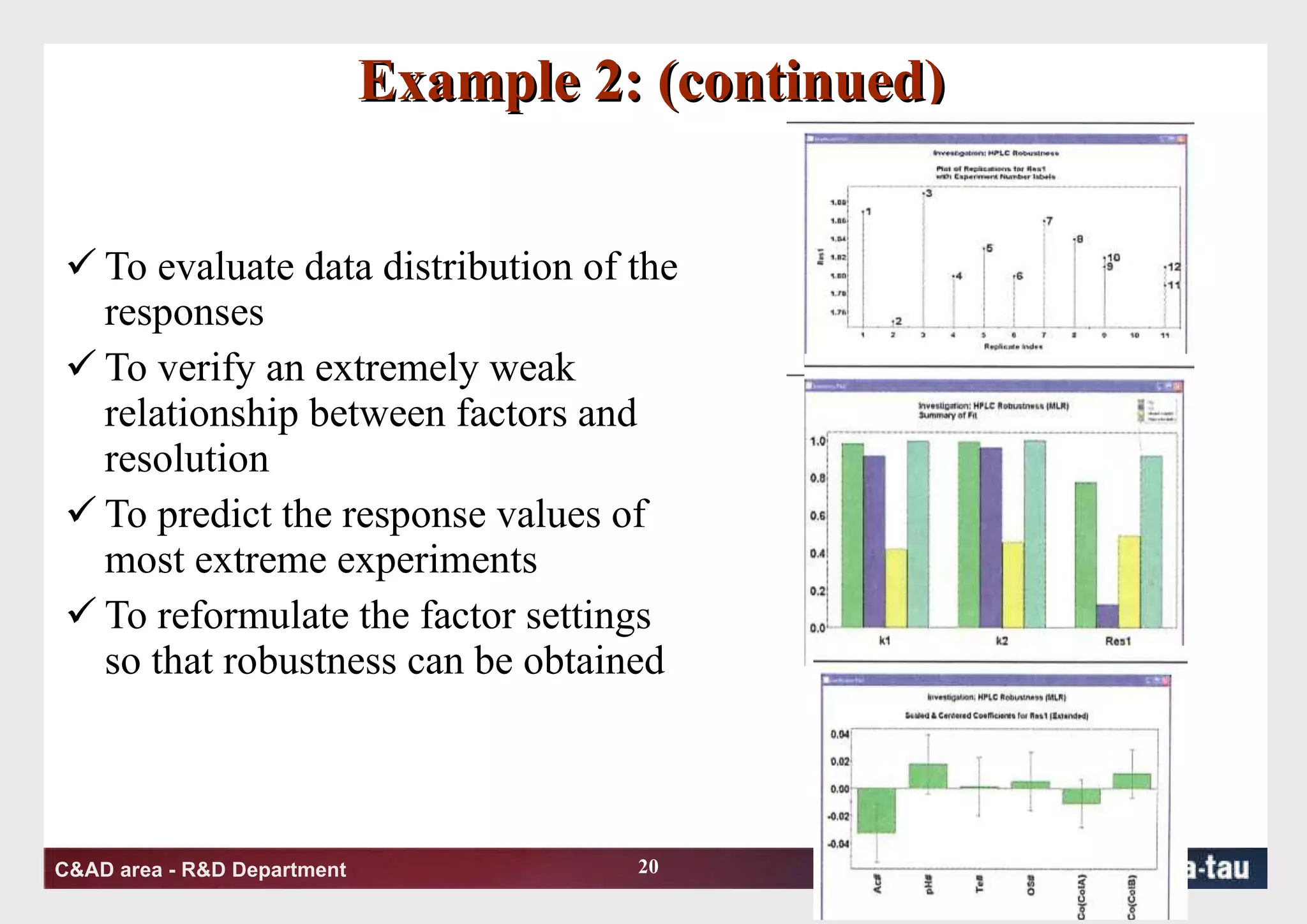
This document discusses Quality by Design (QbD) principles and Design of Experiments (DOE) methodology. It explains that QbD aims to design quality into products and processes through an understanding of key factors and their interactions. DOE provides a systematic approach to determine these factors and optimize conditions through carefully designed experiments. Common DOE steps include screening experiments to identify important factors, followed by optimization experiments to determine optimal levels and robustness testing to ensure consistent performance under variations.