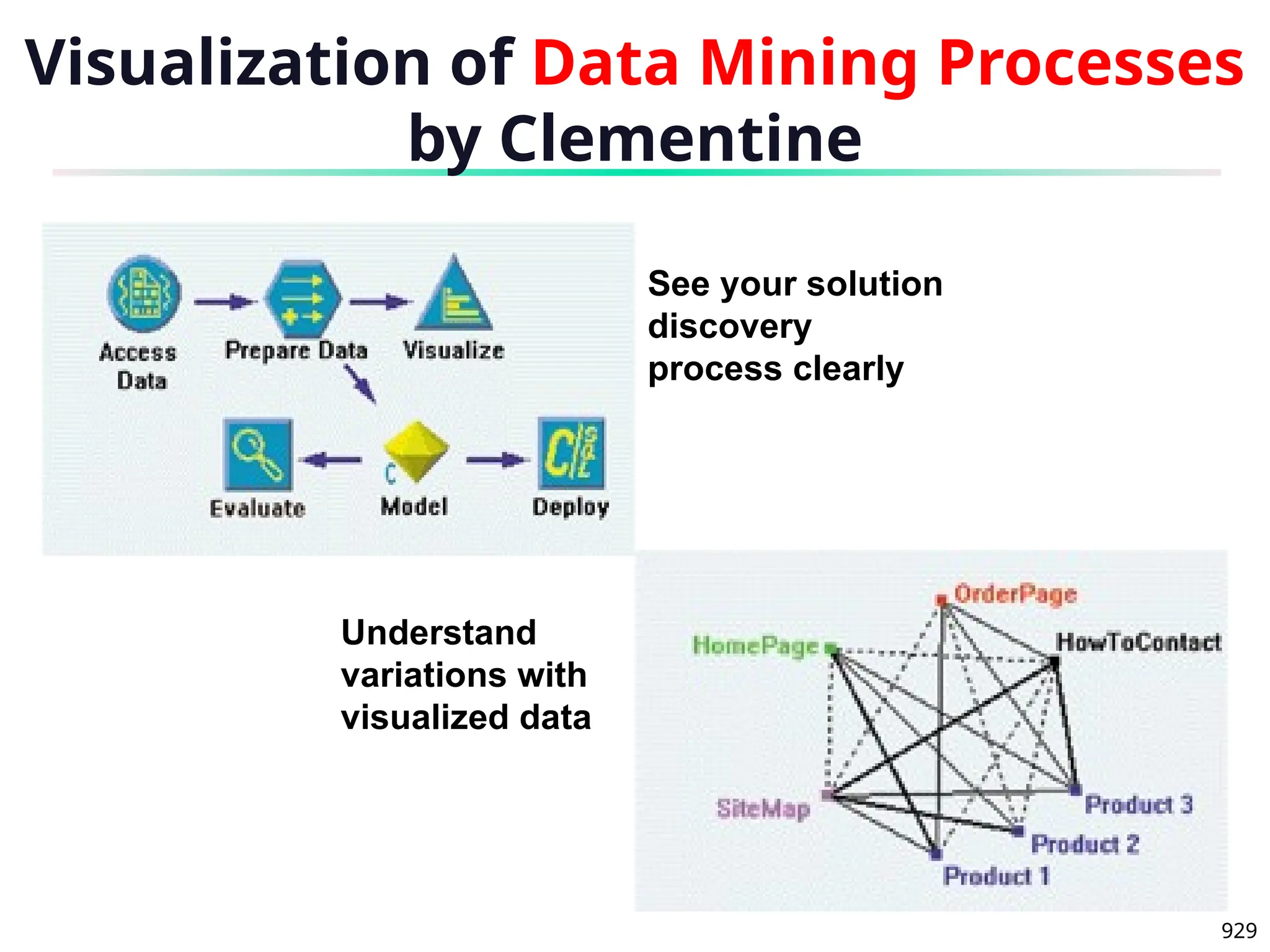
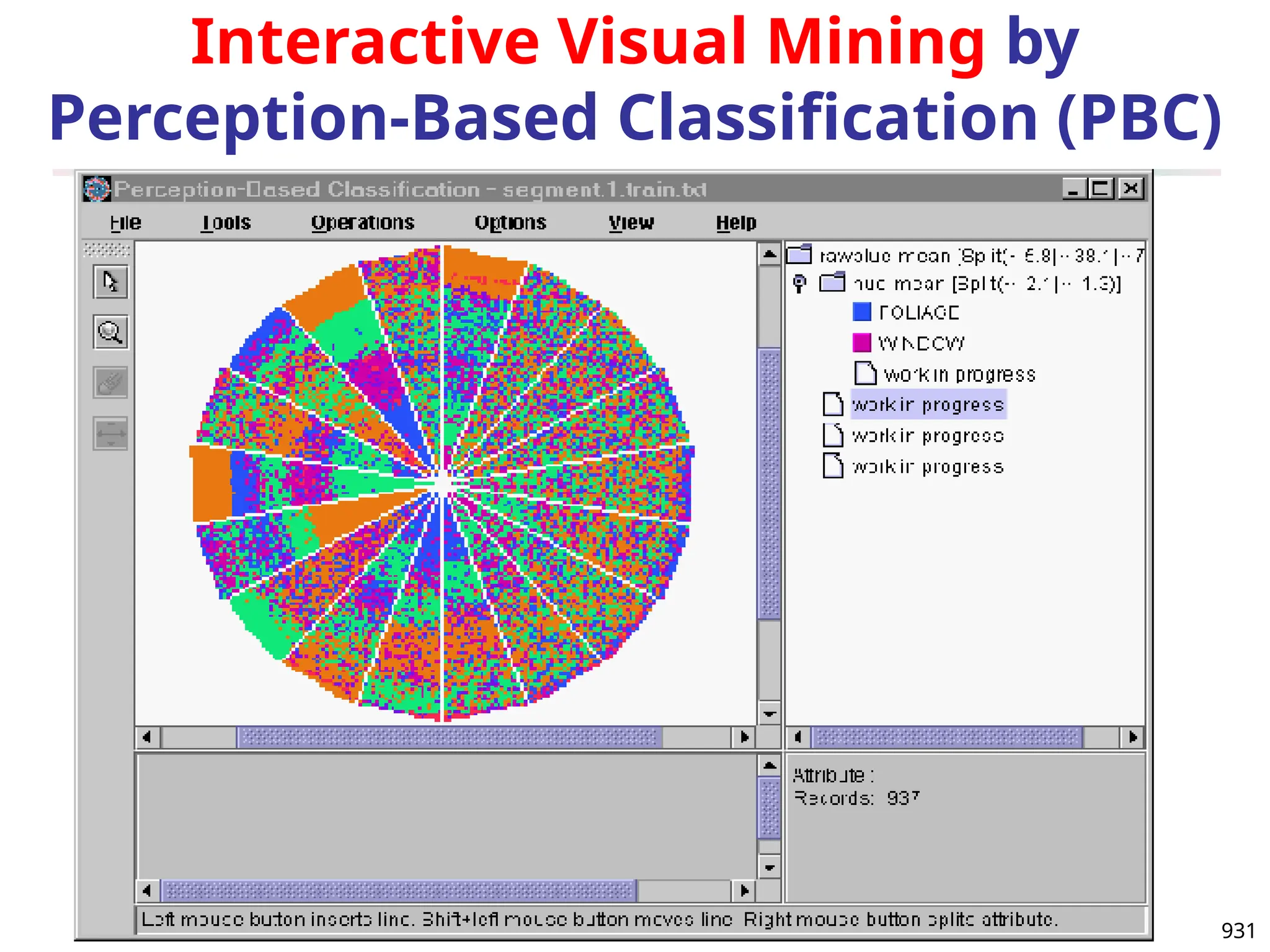
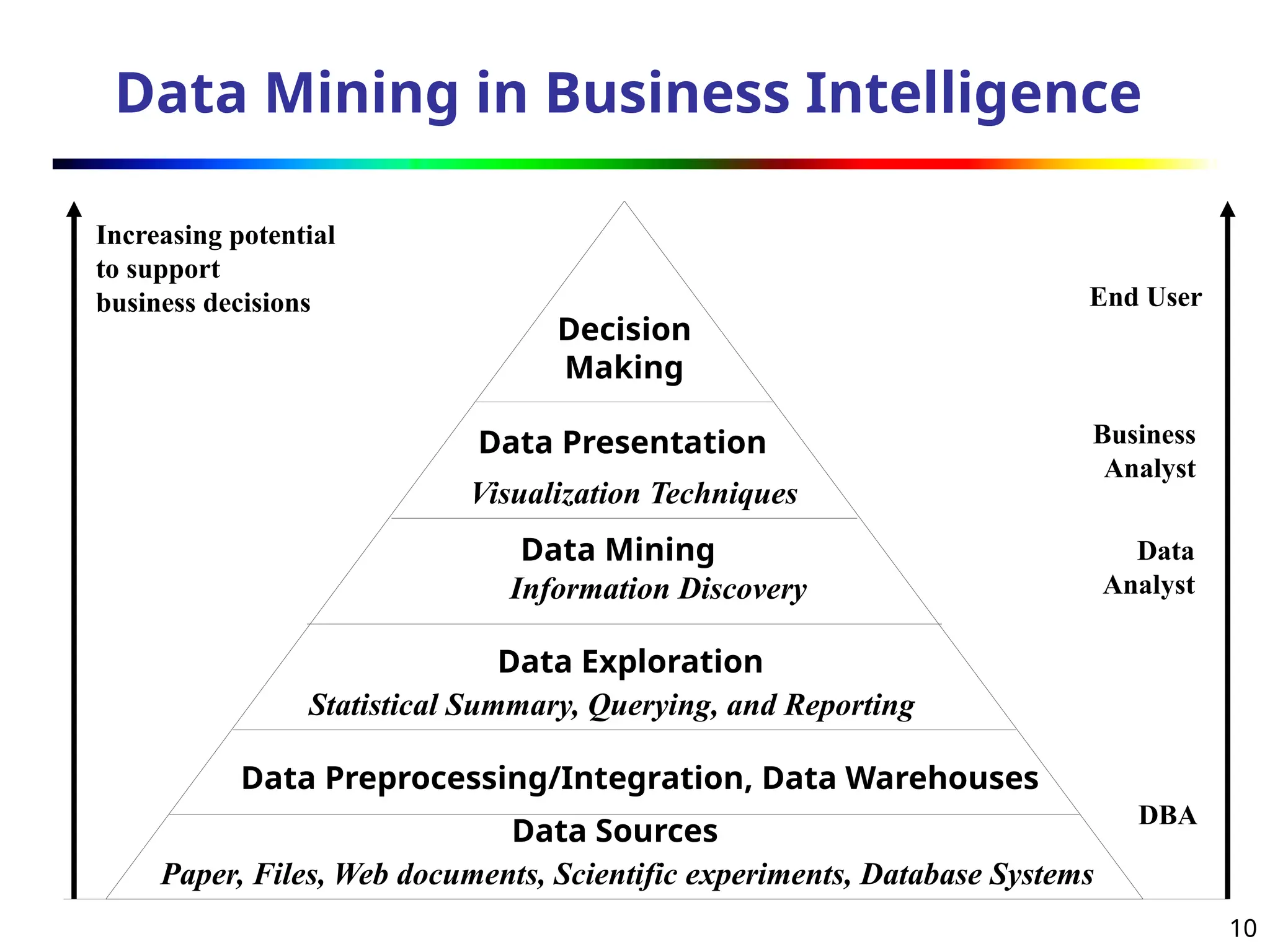
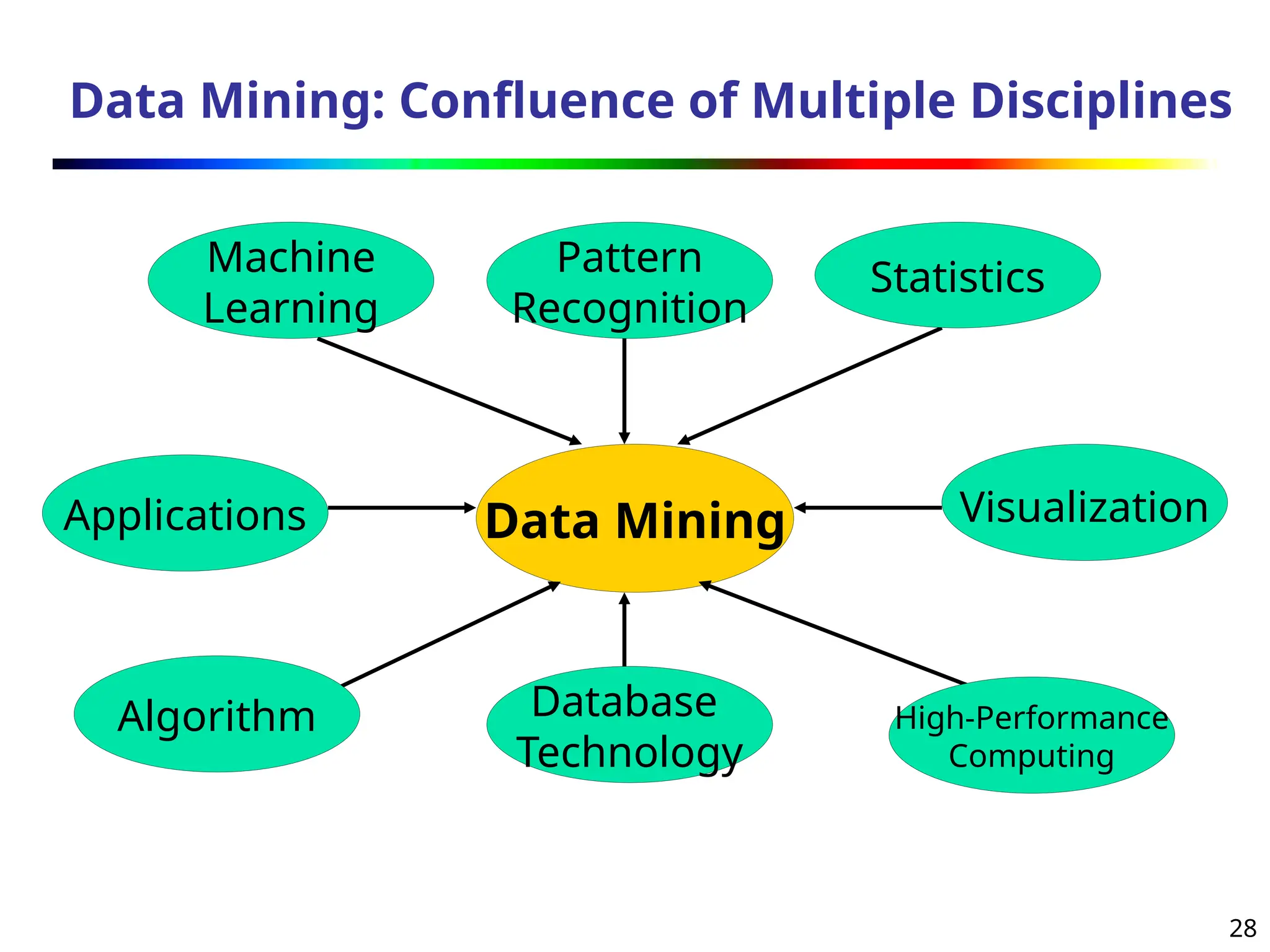
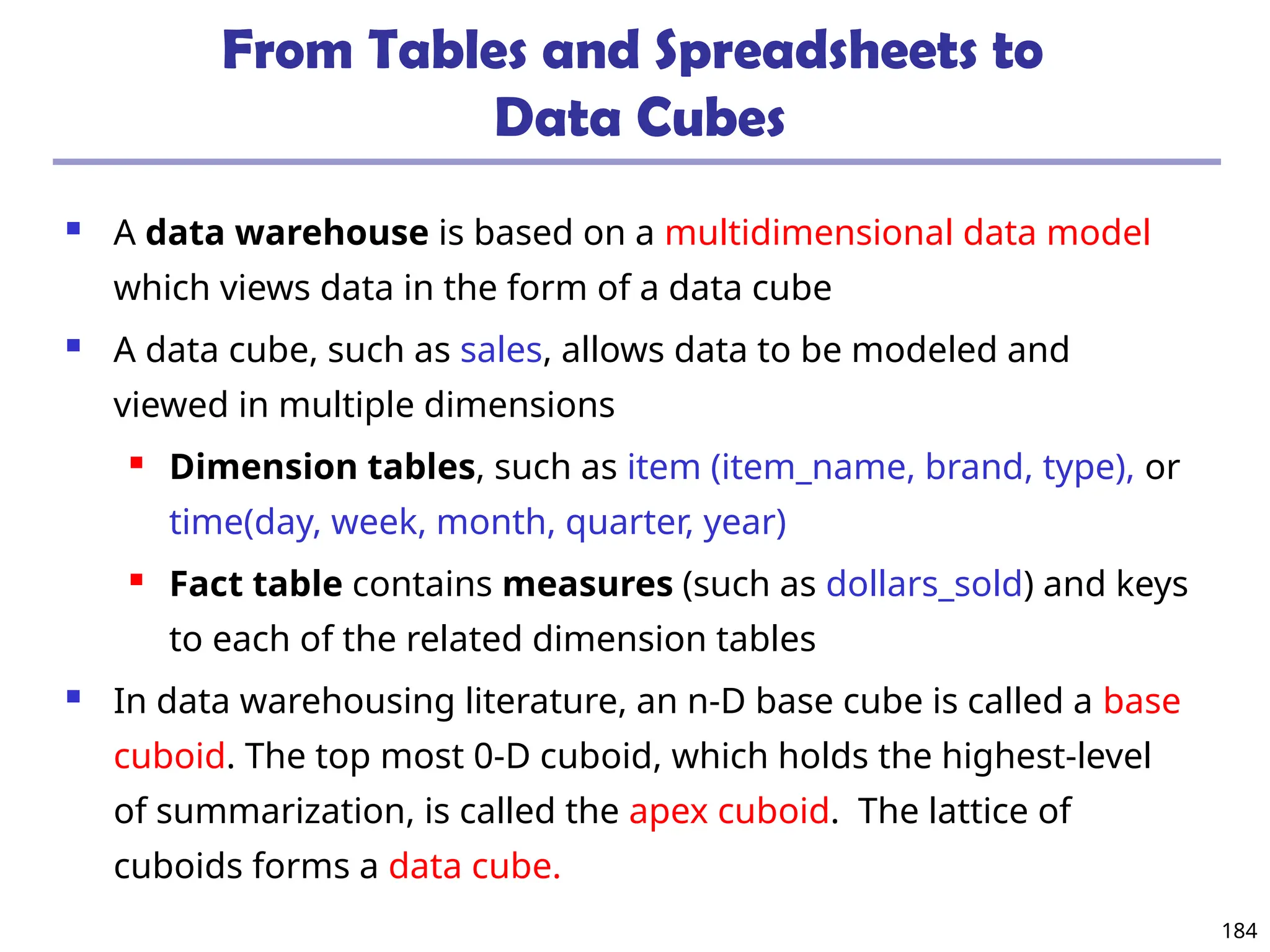
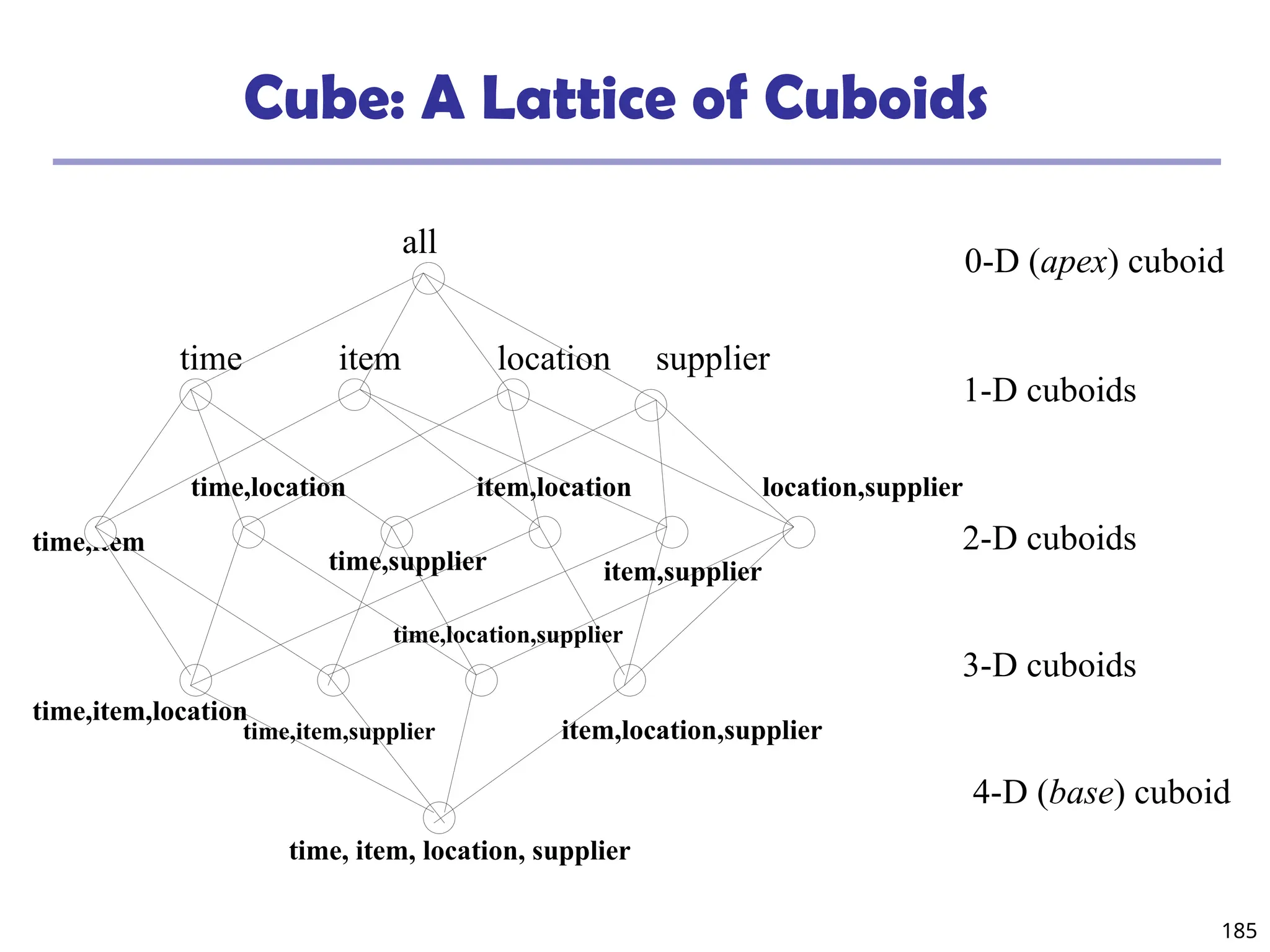
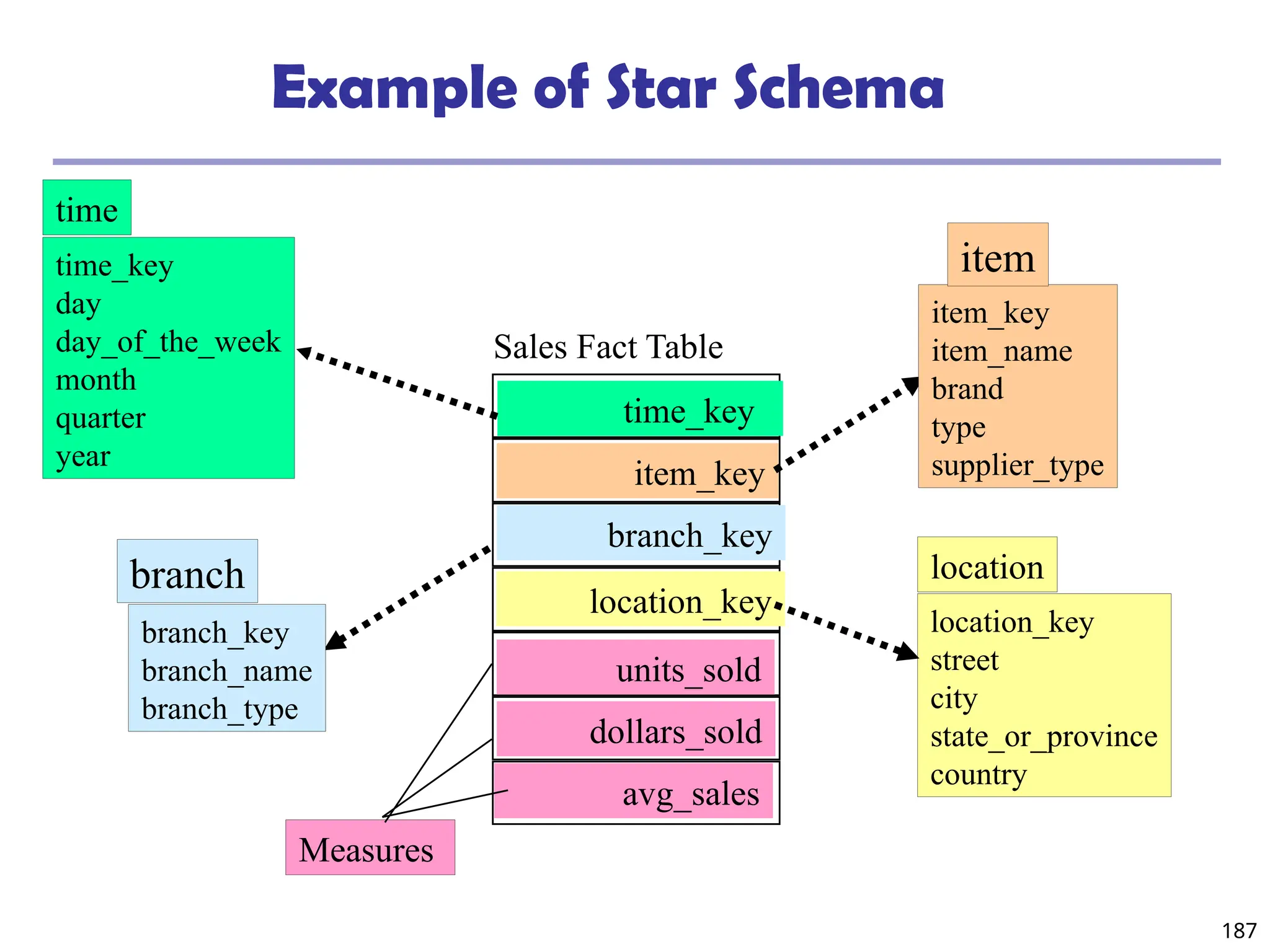
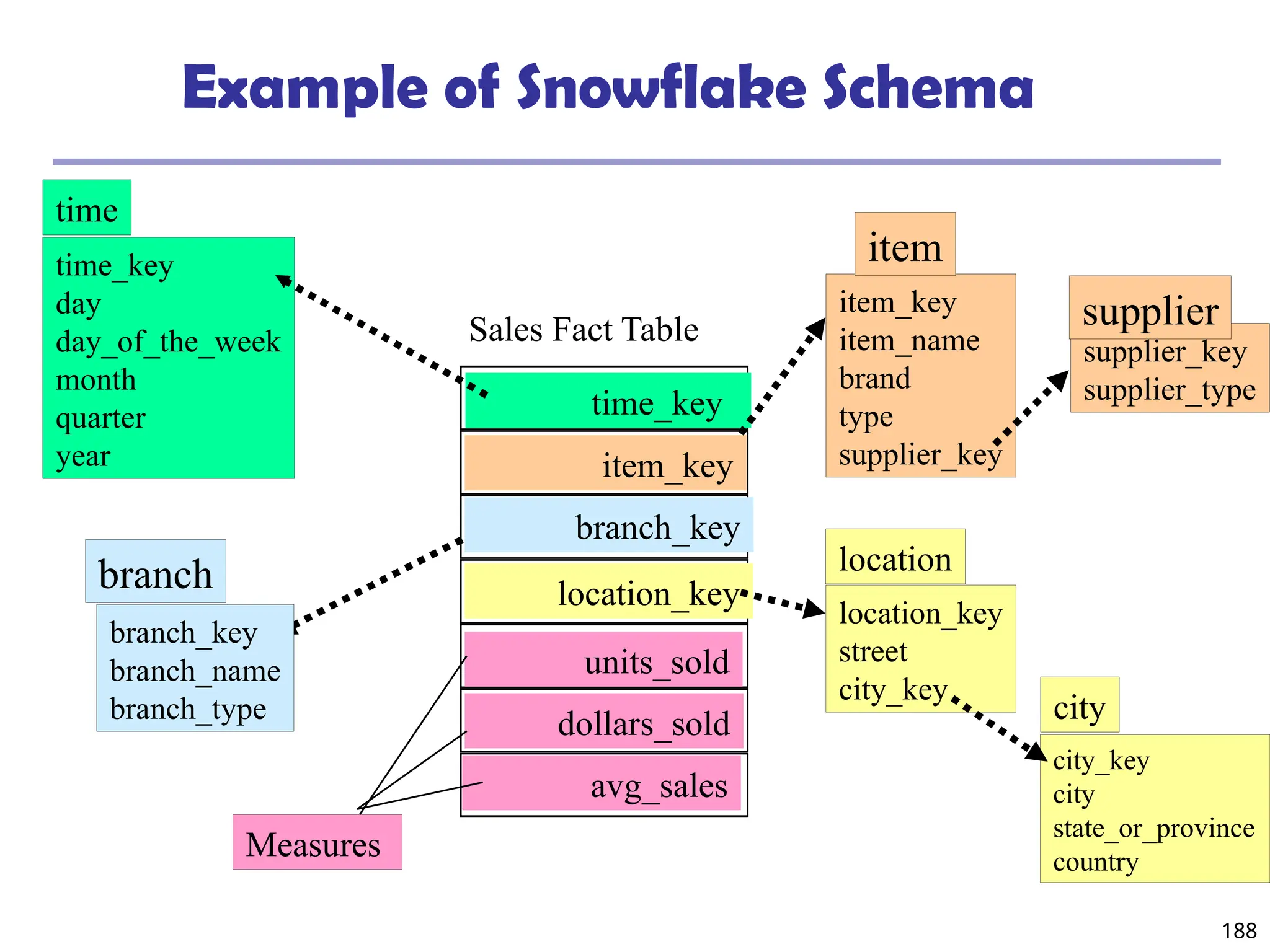
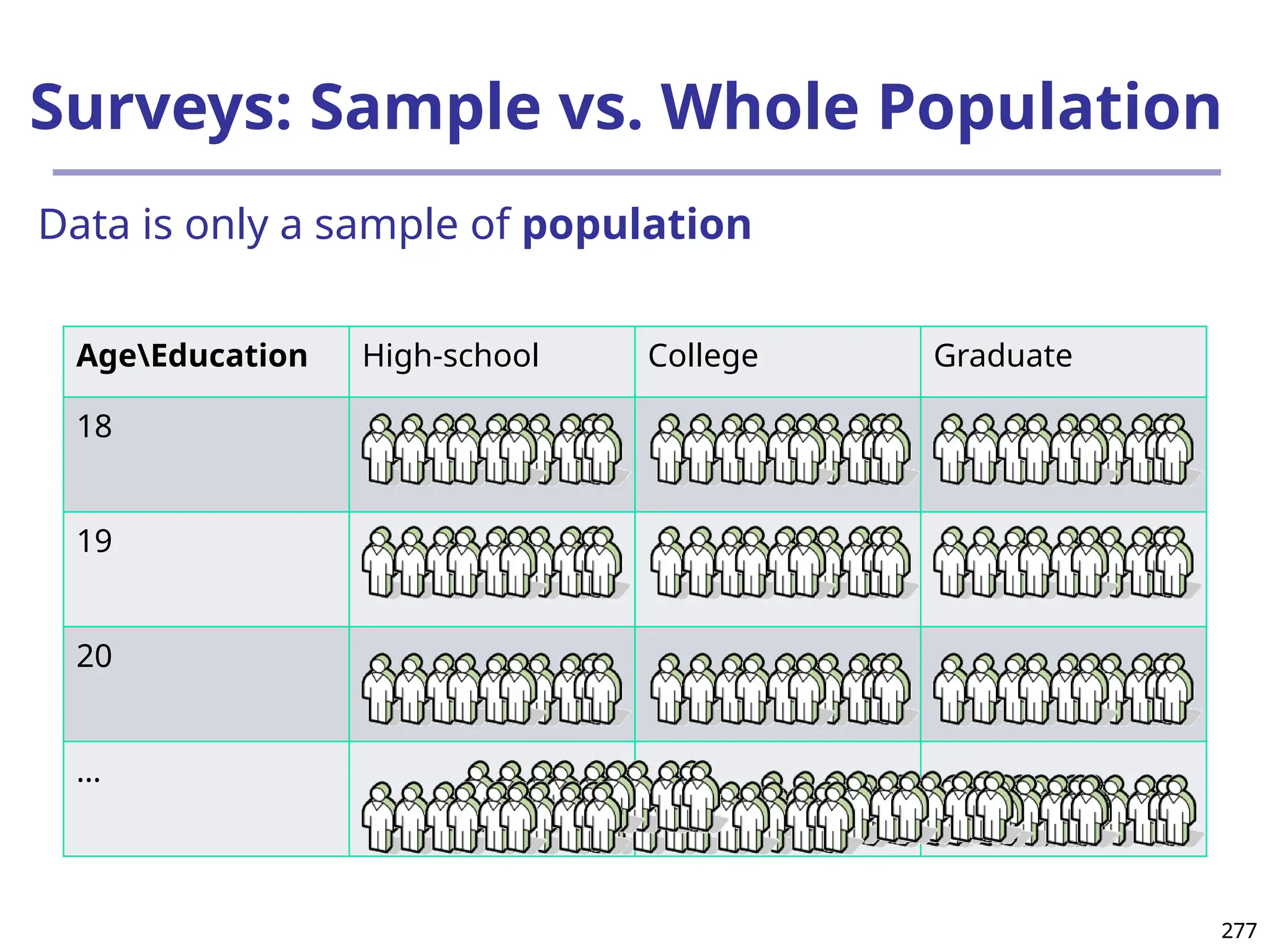
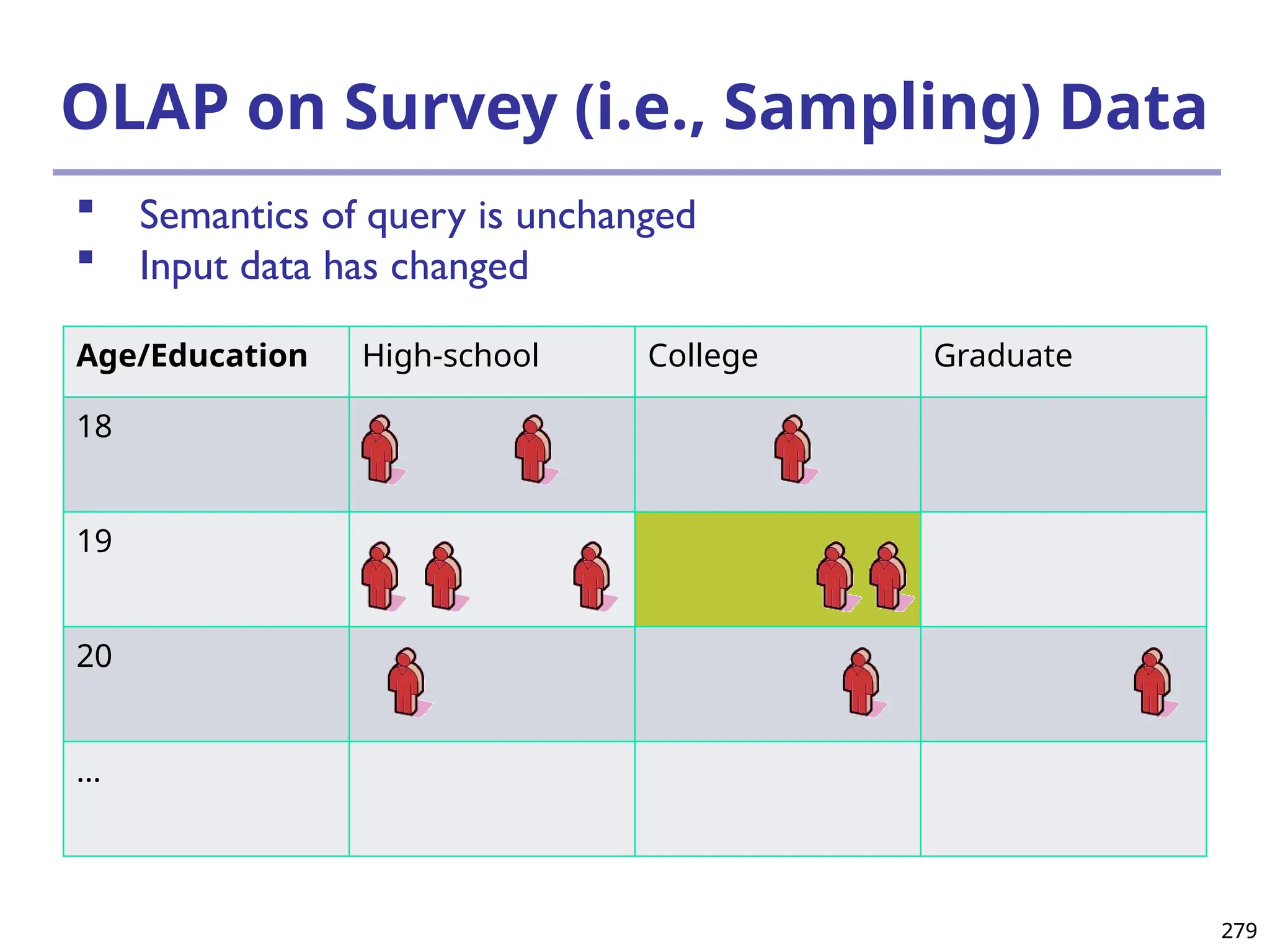
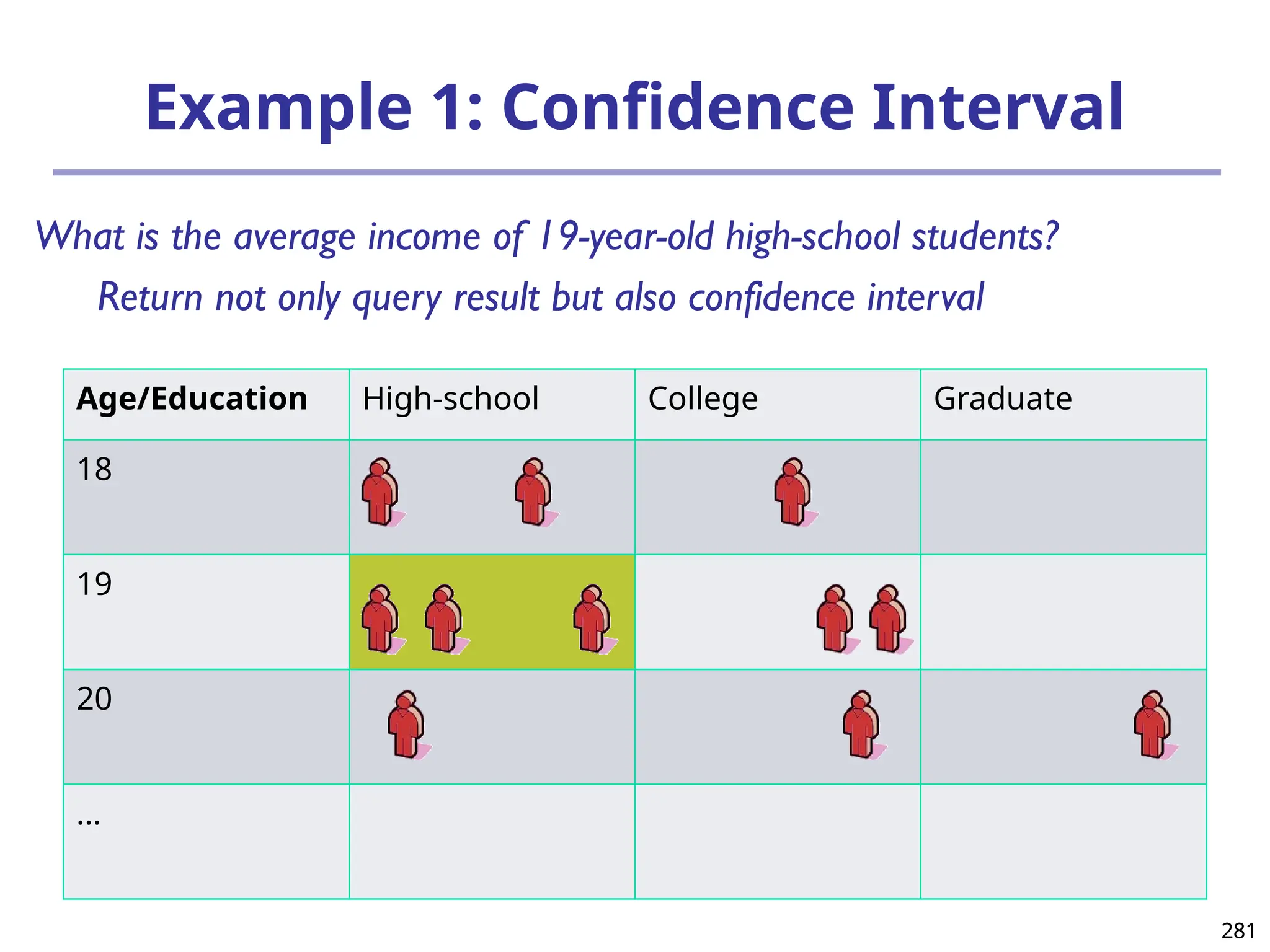
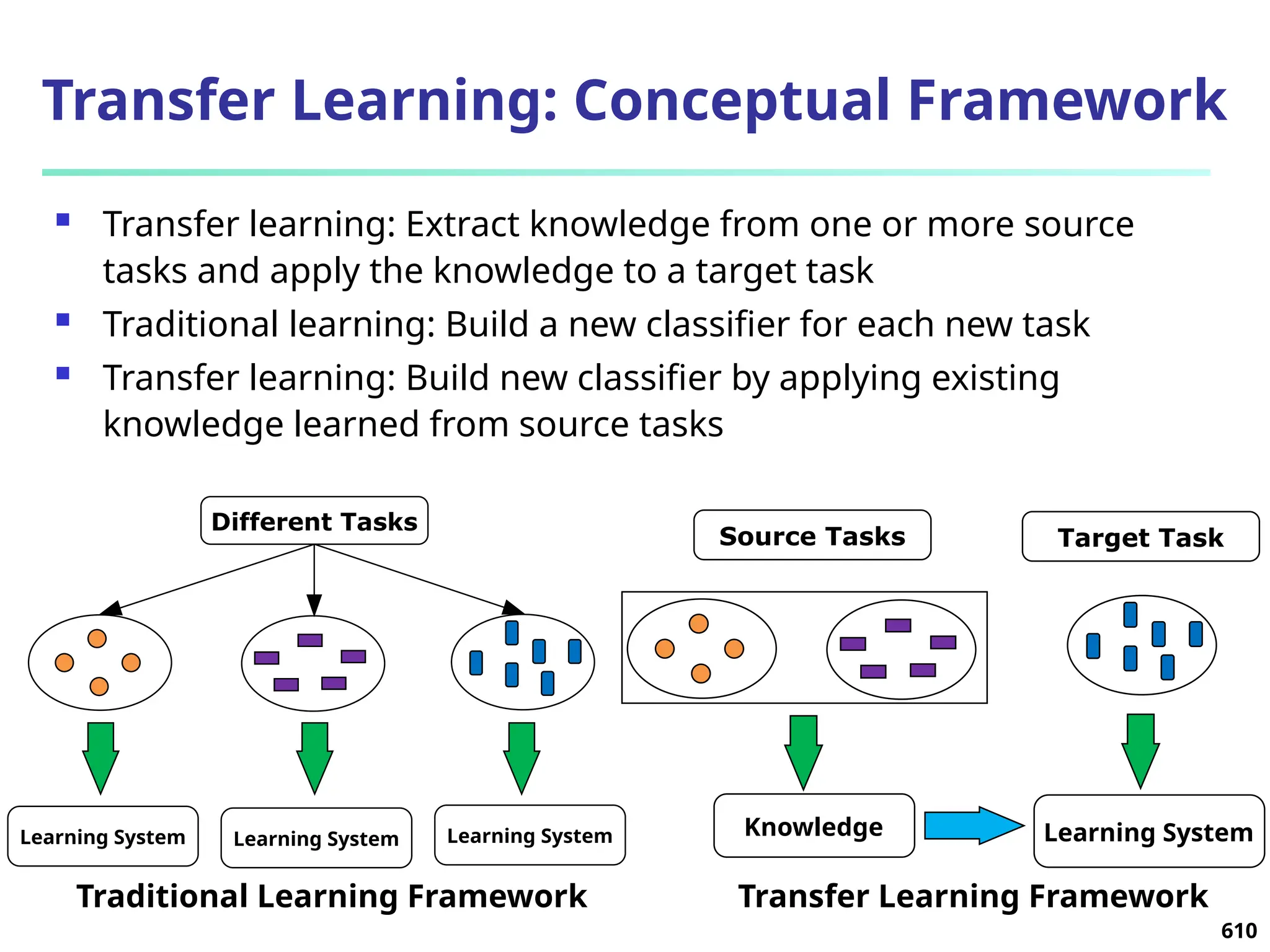
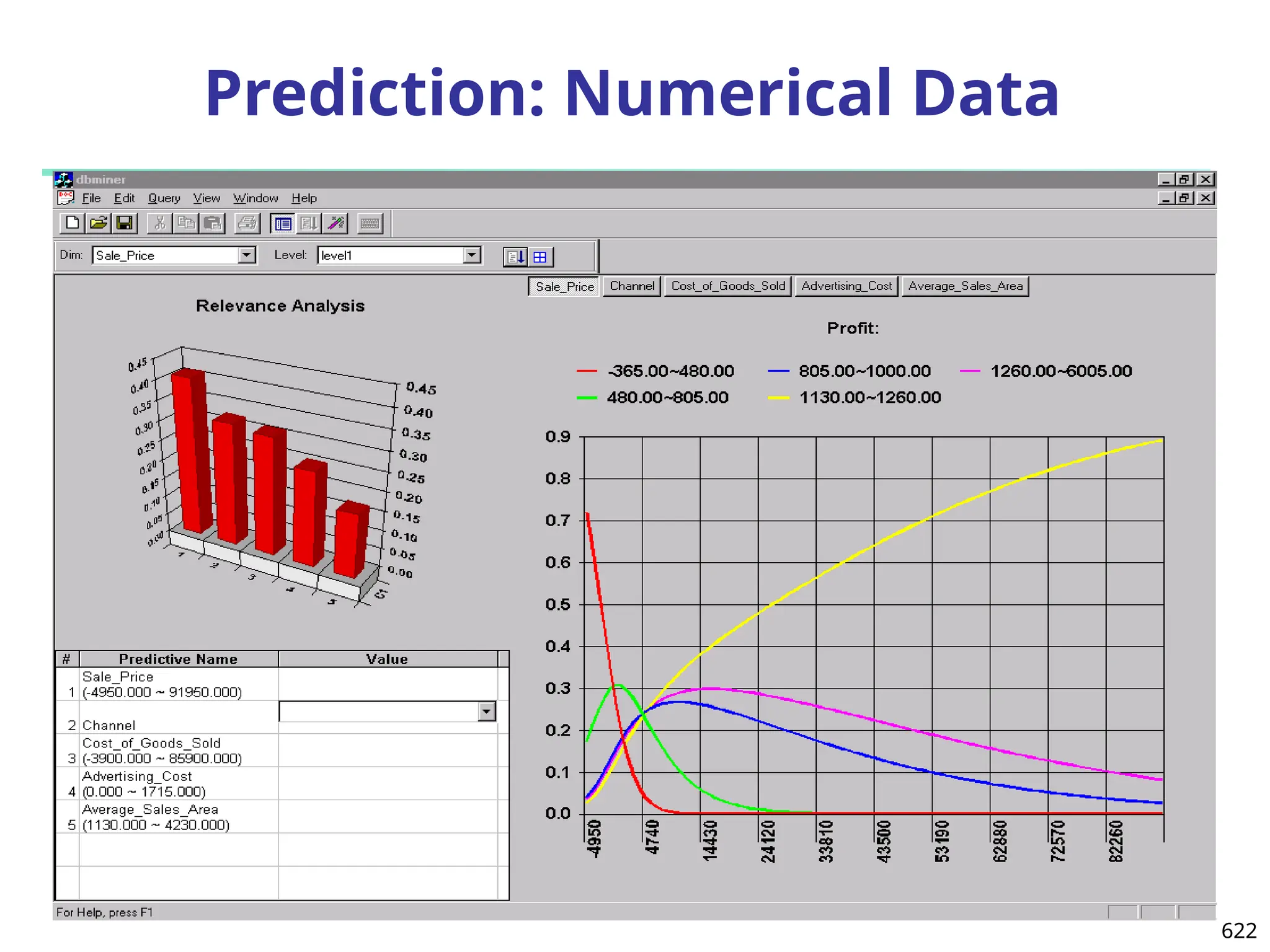
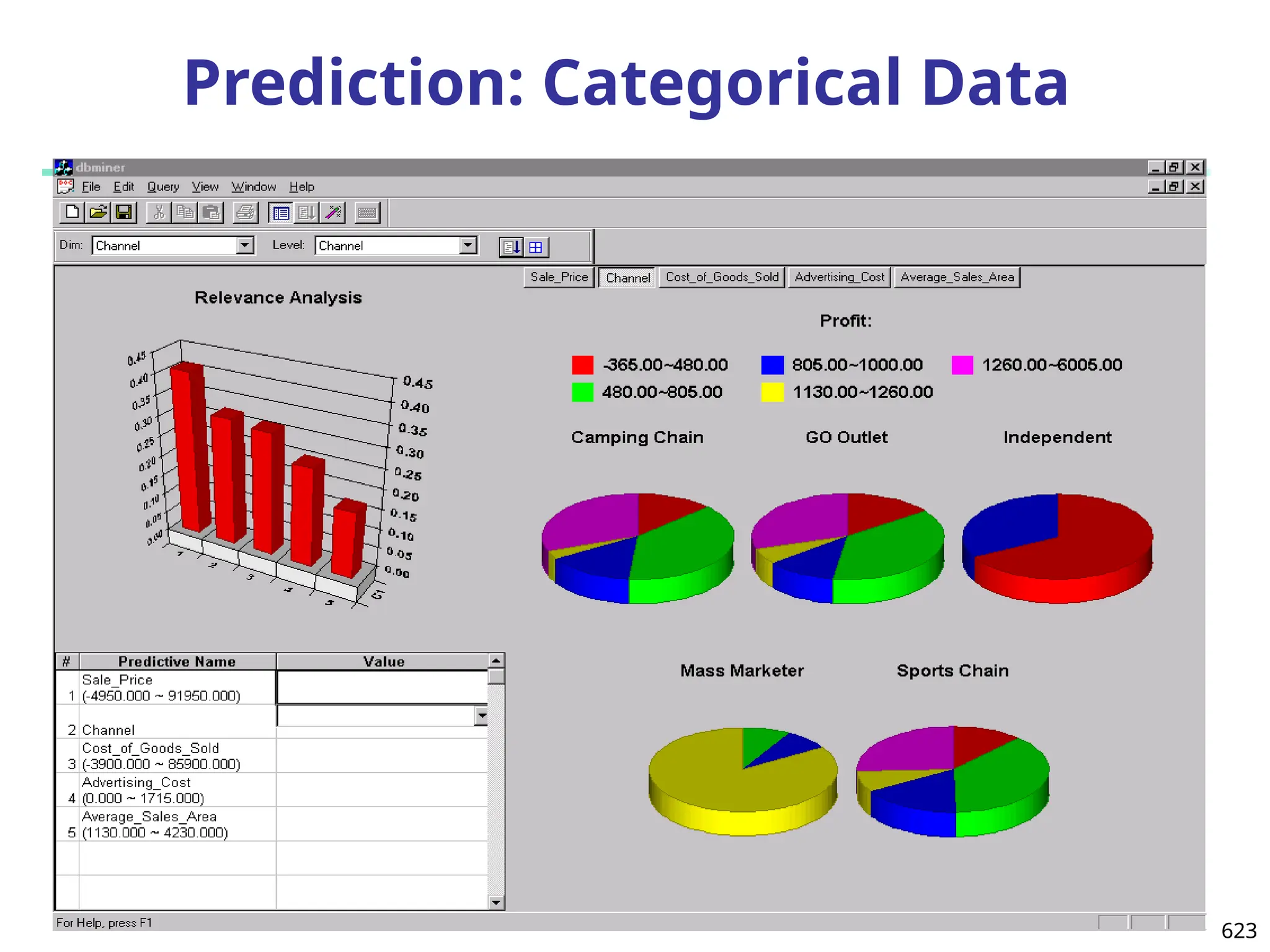
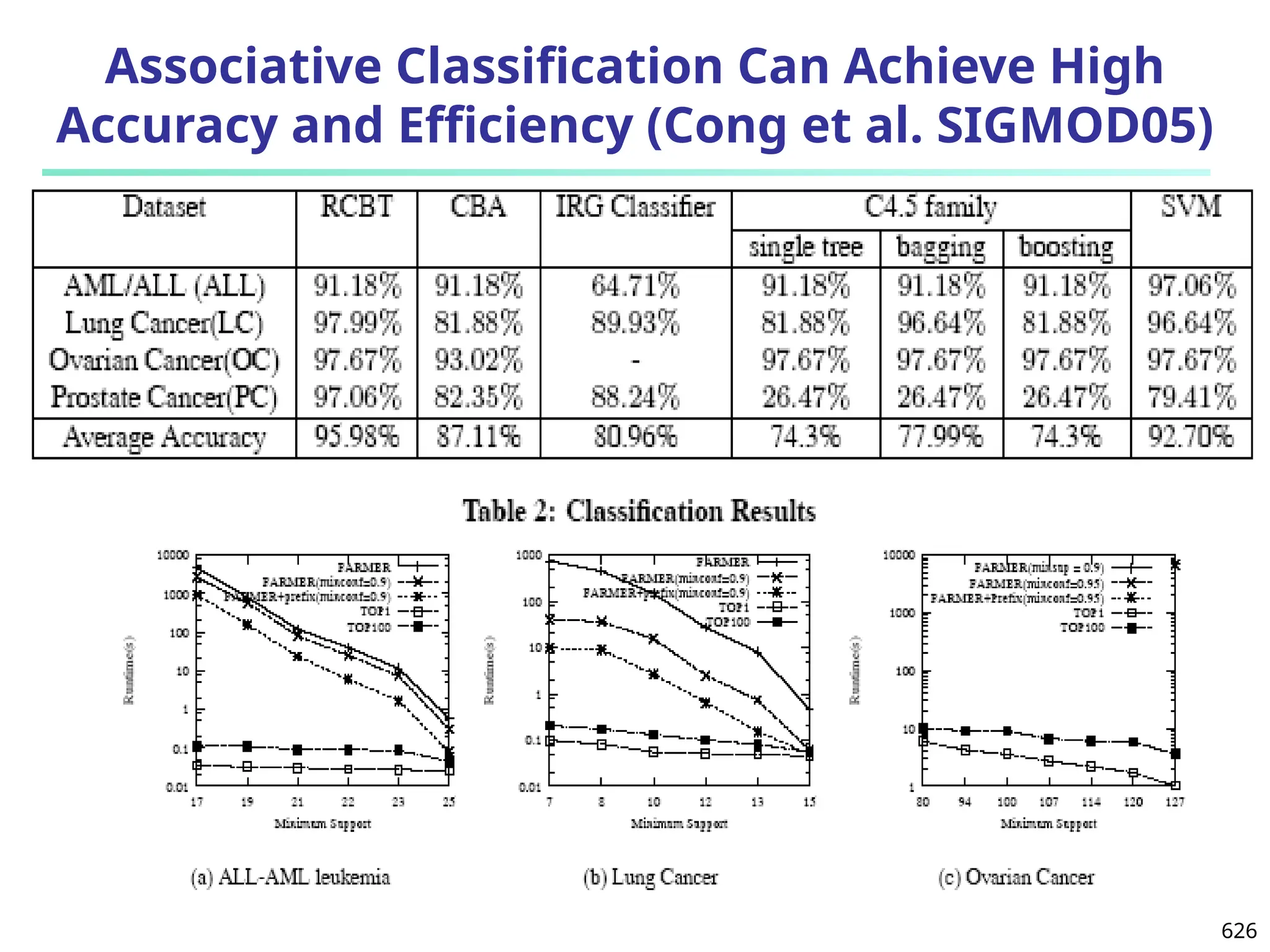
The document introduces data mining, defining it as the extraction of useful patterns from large datasets. It explores the evolution of data science and database technologies, discusses various data types and mining functions, and highlights applications across domains such as business and healthcare. Key issues in data mining, including efficiency, scalability, and methodology, are also addressed along with a brief history of the data mining community.


















![20
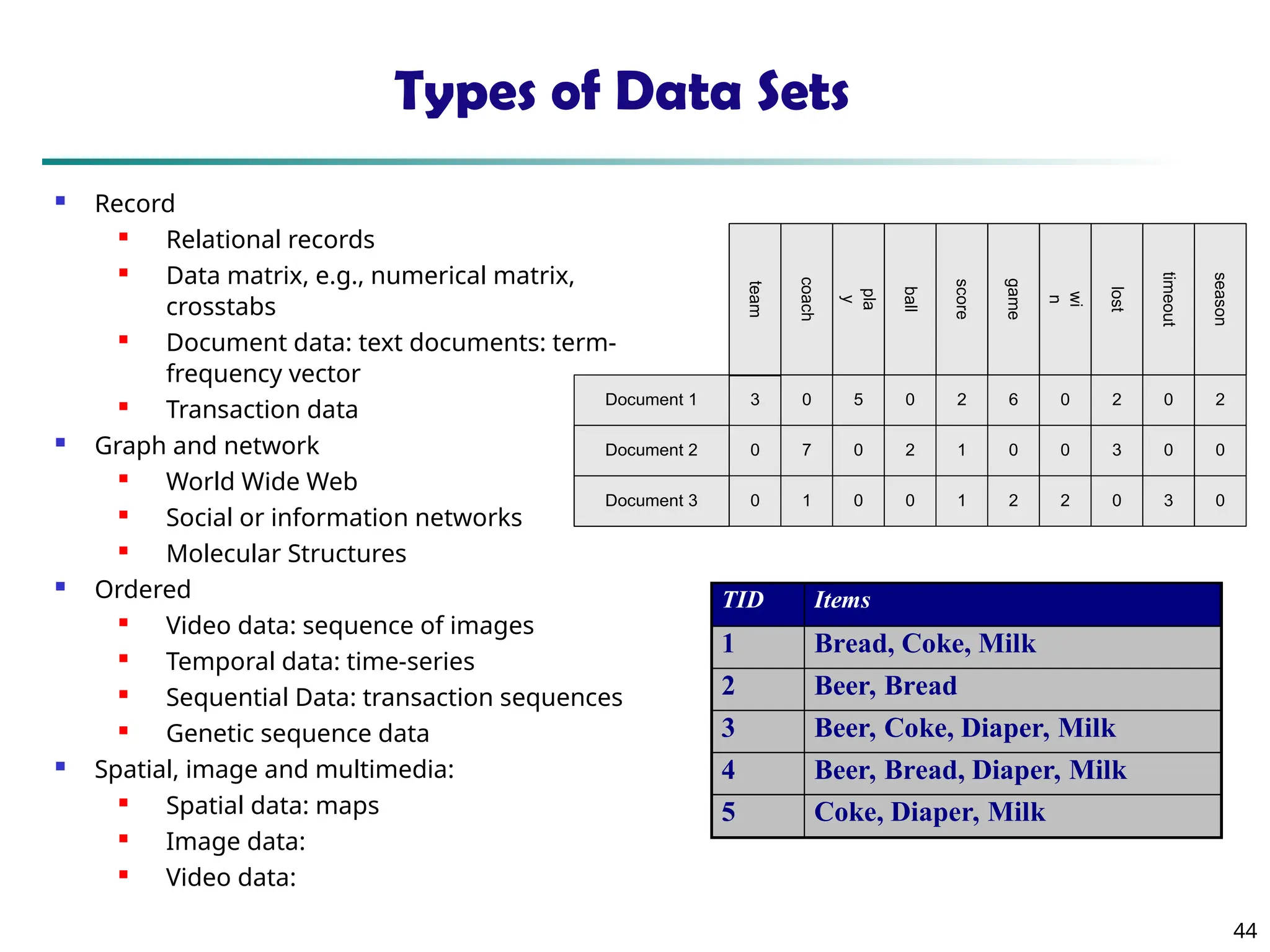
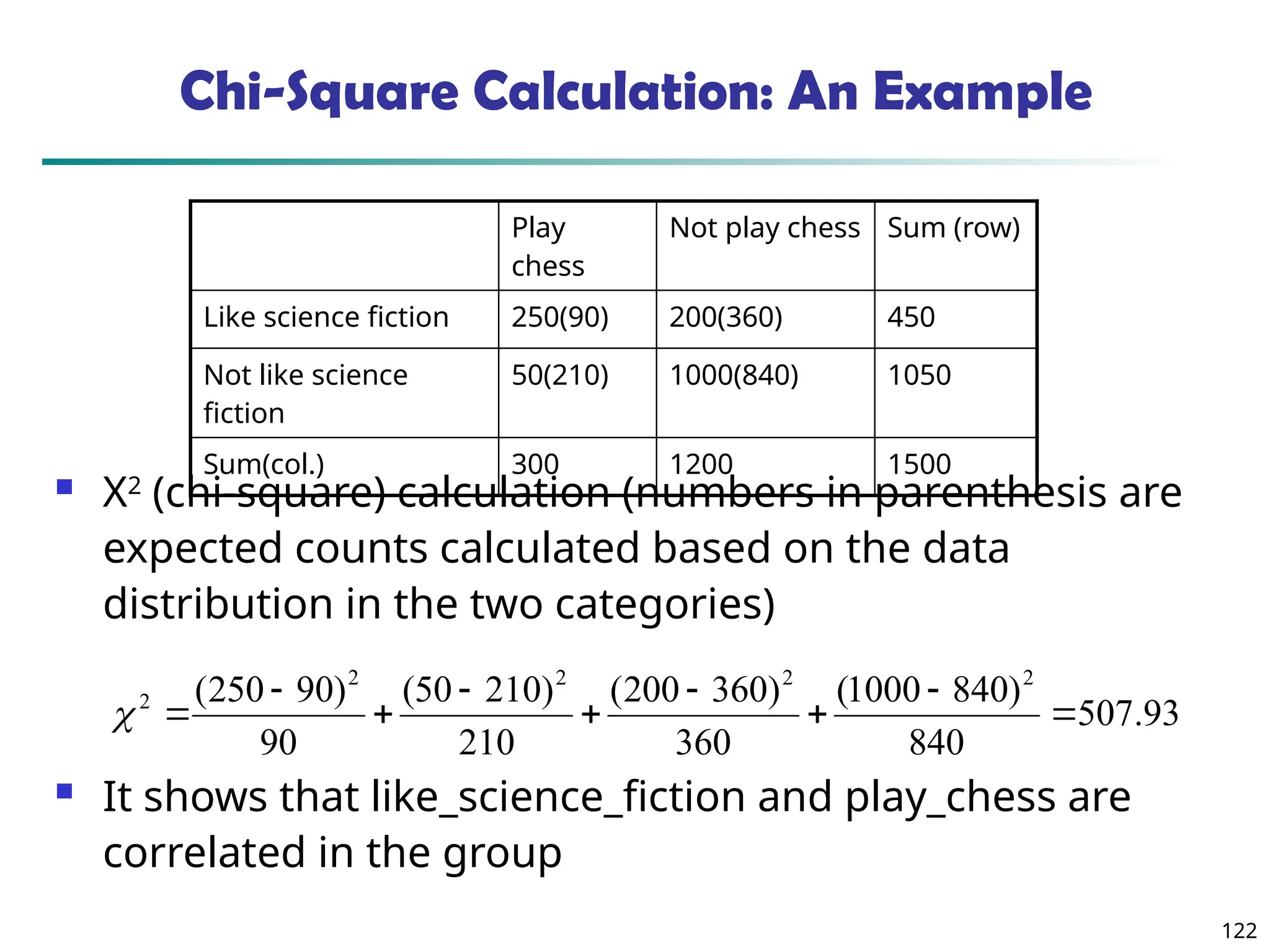
Data Mining Function: (2) Association and
Correlation Analysis
Frequent patterns (or frequent itemsets)
What items are frequently purchased together in
your Walmart?
Association, correlation vs. causality
A typical association rule
Diaper Beer [0.5%, 75%] (support,
confidence)
Are strongly associated items also strongly
correlated?
How to mine such patterns and rules efficiently in
large datasets?
How to use such patterns for classification, clustering,](https://image.slidesharecdn.com/dwdm3rdeditiontextbookslides-241024155956-ed696a42/75/DWDM-3rd-EDITION-TEXT-BOOK-SLIDES24-pptx-20-2048.jpg)






























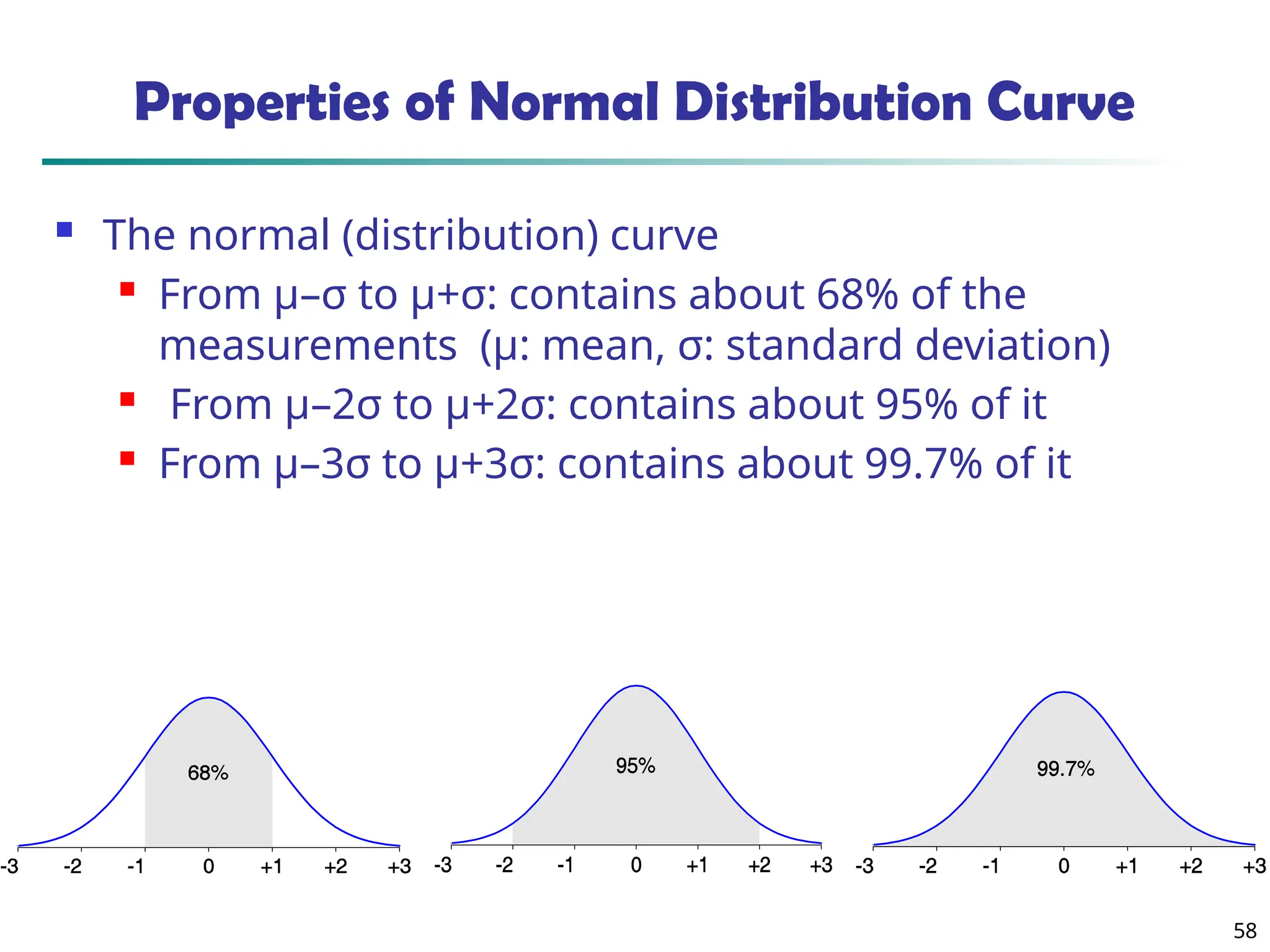
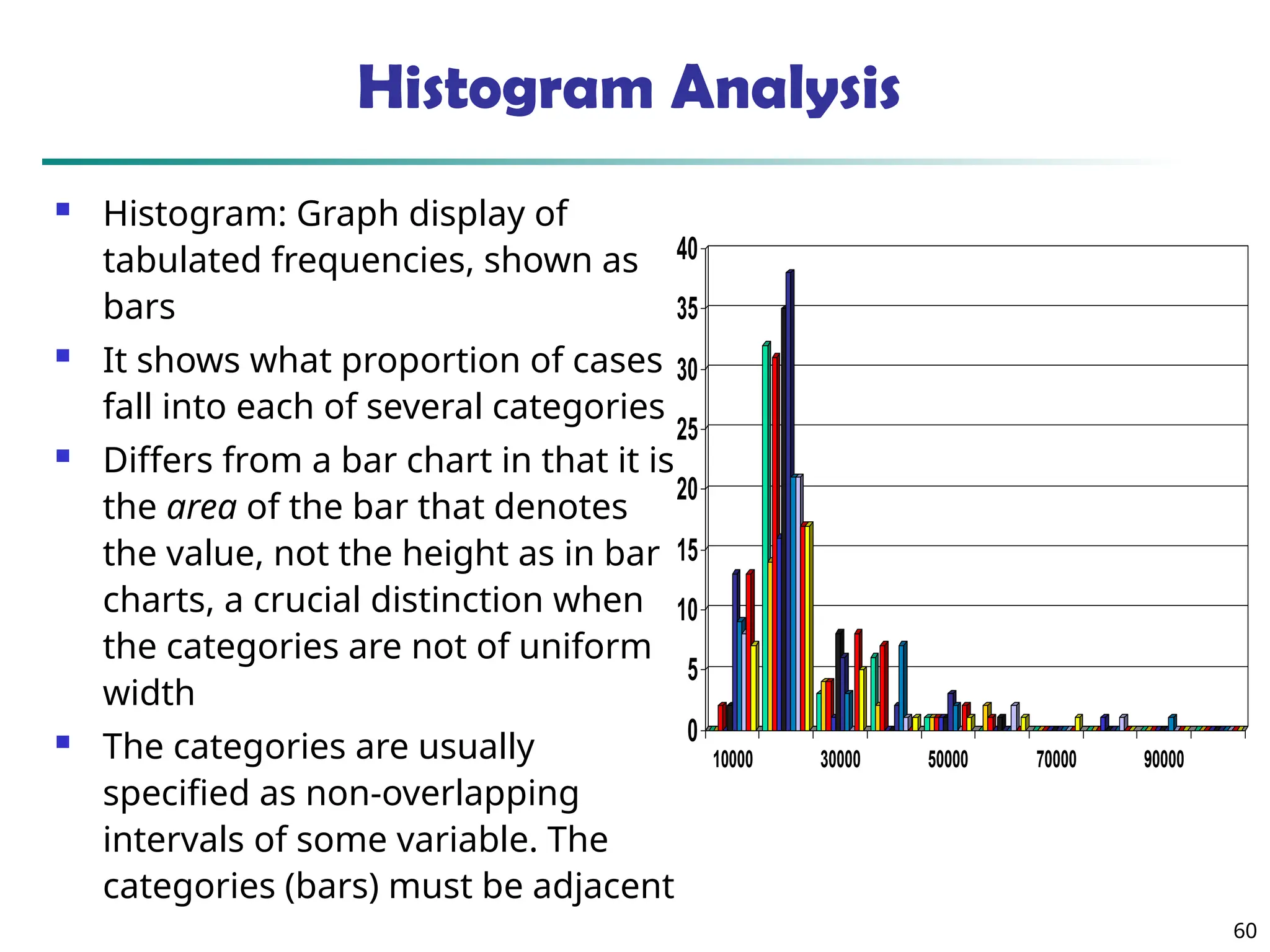
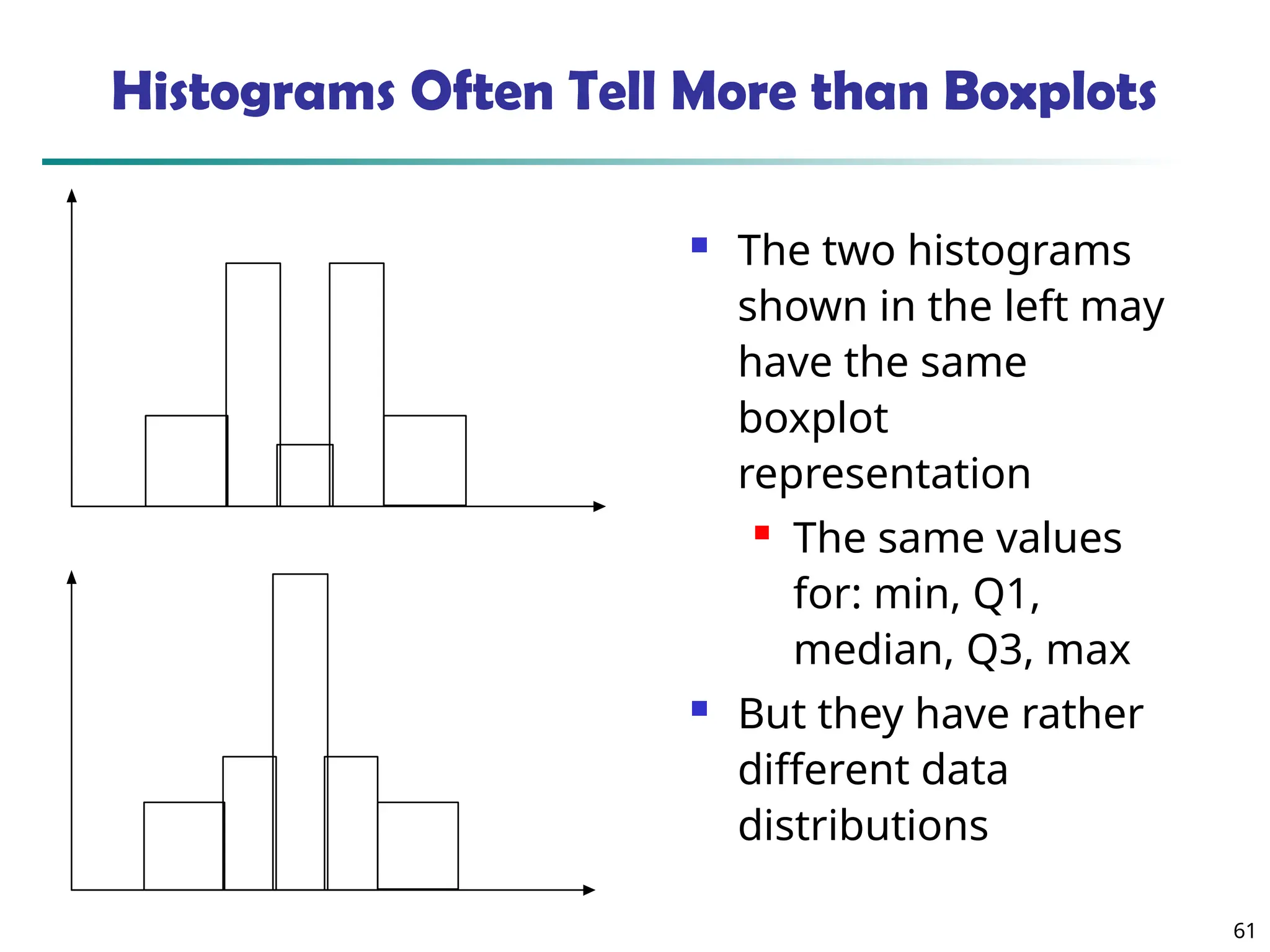
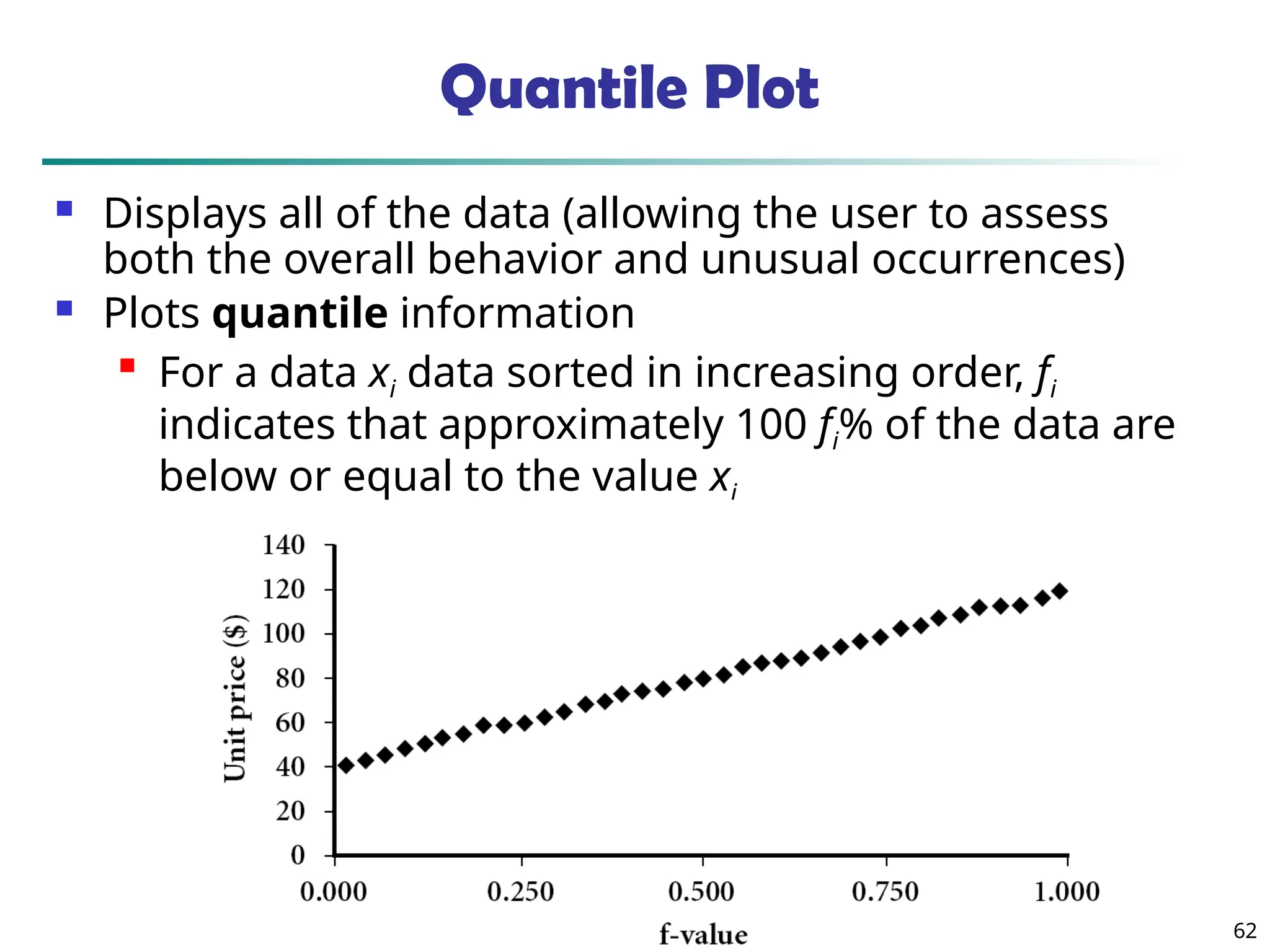
![55
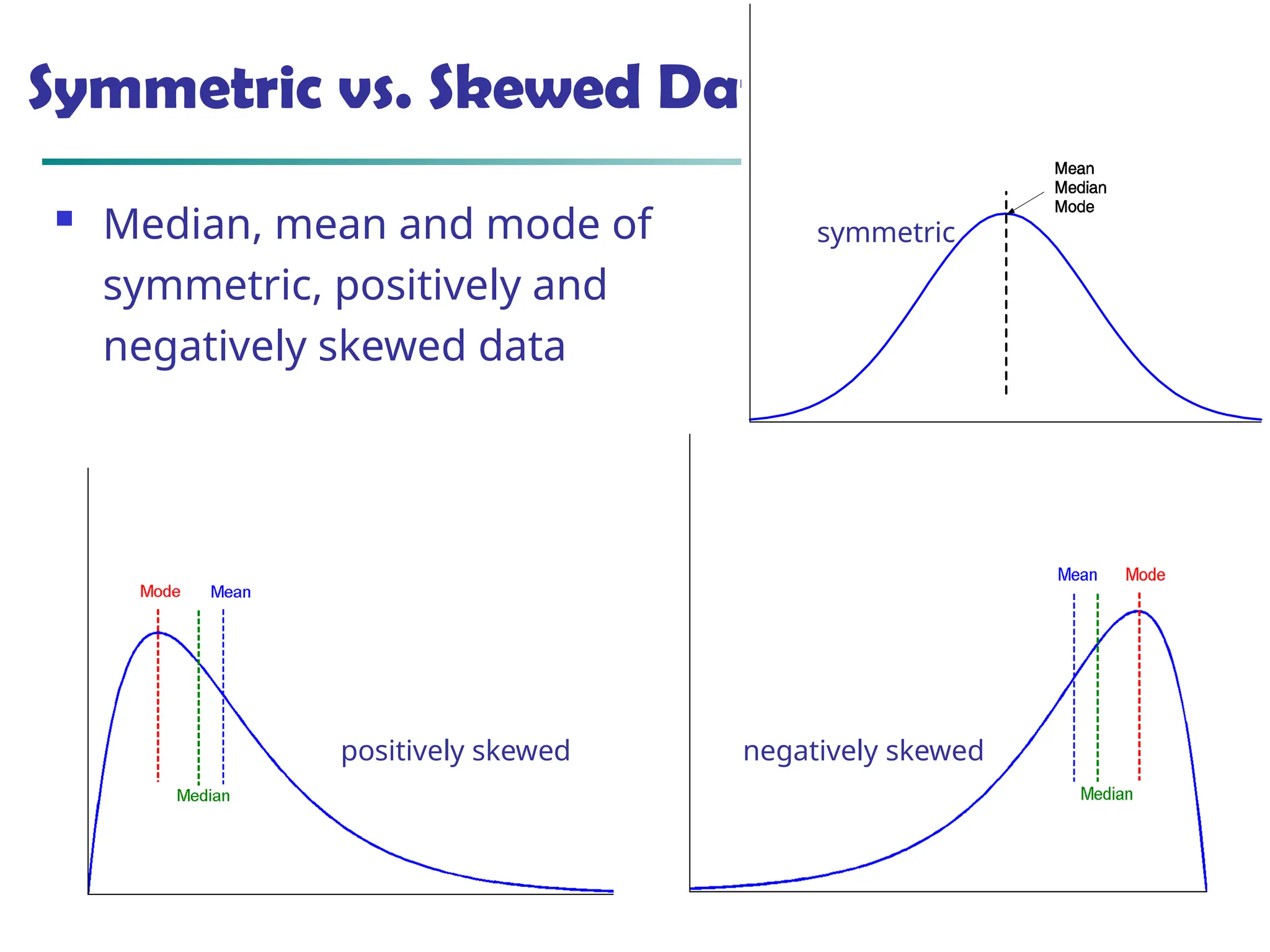
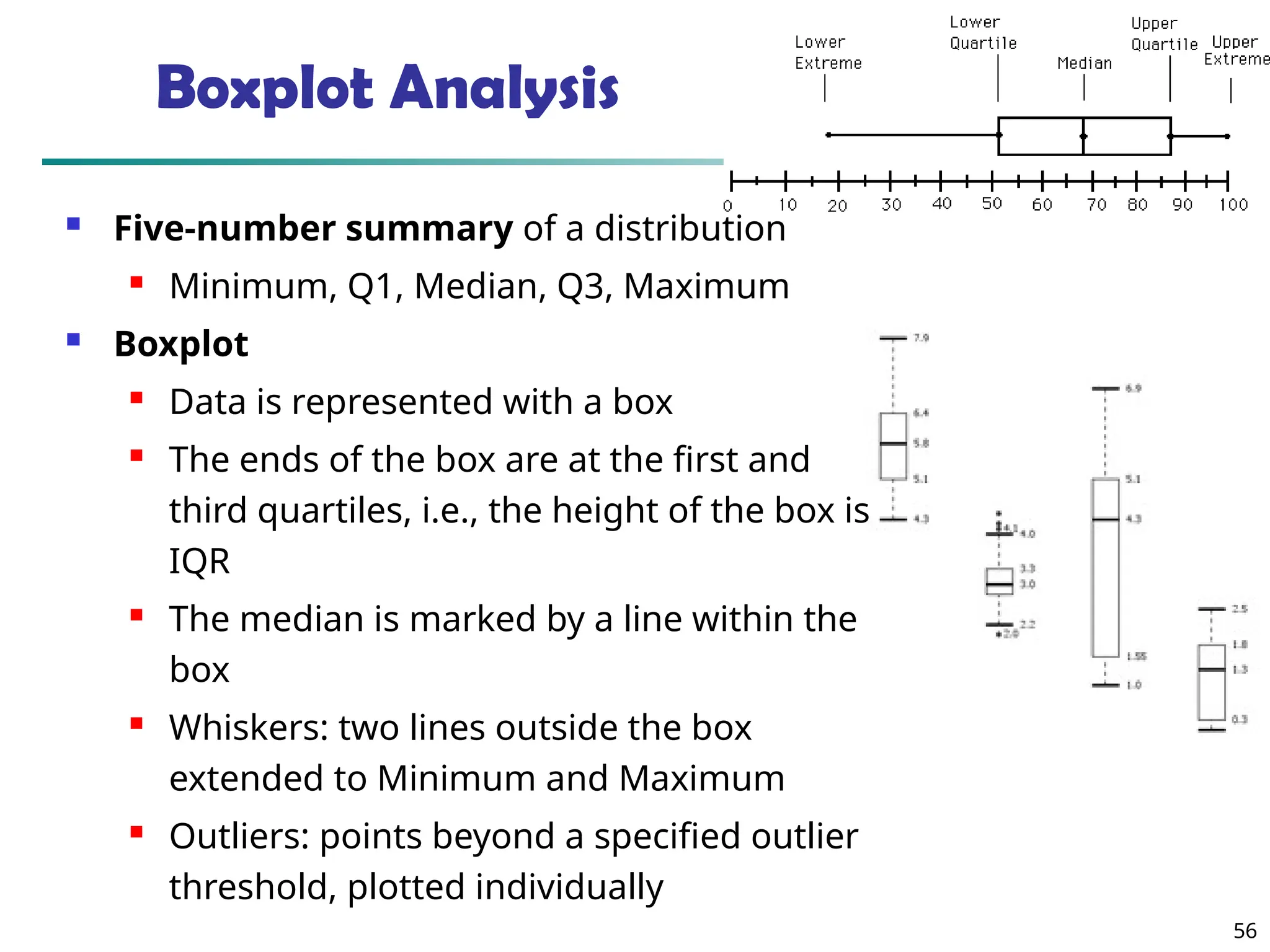
Measuring the Dispersion of Data
Quartiles, outliers and boxplots
Quartiles: Q1 (25th
percentile), Q3 (75th
percentile)
Inter-quartile range: IQR = Q3 –Q1
Five number summary: min, Q1, median, Q3, max
Boxplot: ends of the box are the quartiles; median is marked; add
whiskers, and plot outliers individually
Outlier: usually, a value higher/lower than 1.5 x IQR
Variance and standard deviation (sample: s, population: σ)
Variance: (algebraic, scalable computation)
Standard deviation s (or σ) is the square root of variance s2 (
or σ2)
n
i
n
i
i
i
n
i
i x
n
x
n
x
x
n
s
1 1
2
2
1
2
2
]
)
(
1
[
1
1
)
(
1
1
n
i
i
n
i
i x
N
x
N 1
2
2
1
2
2 1
)
(
1
](https://image.slidesharecdn.com/dwdm3rdeditiontextbookslides-241024155956-ed696a42/75/DWDM-3rd-EDITION-TEXT-BOOK-SLIDES24-pptx-55-2048.jpg)
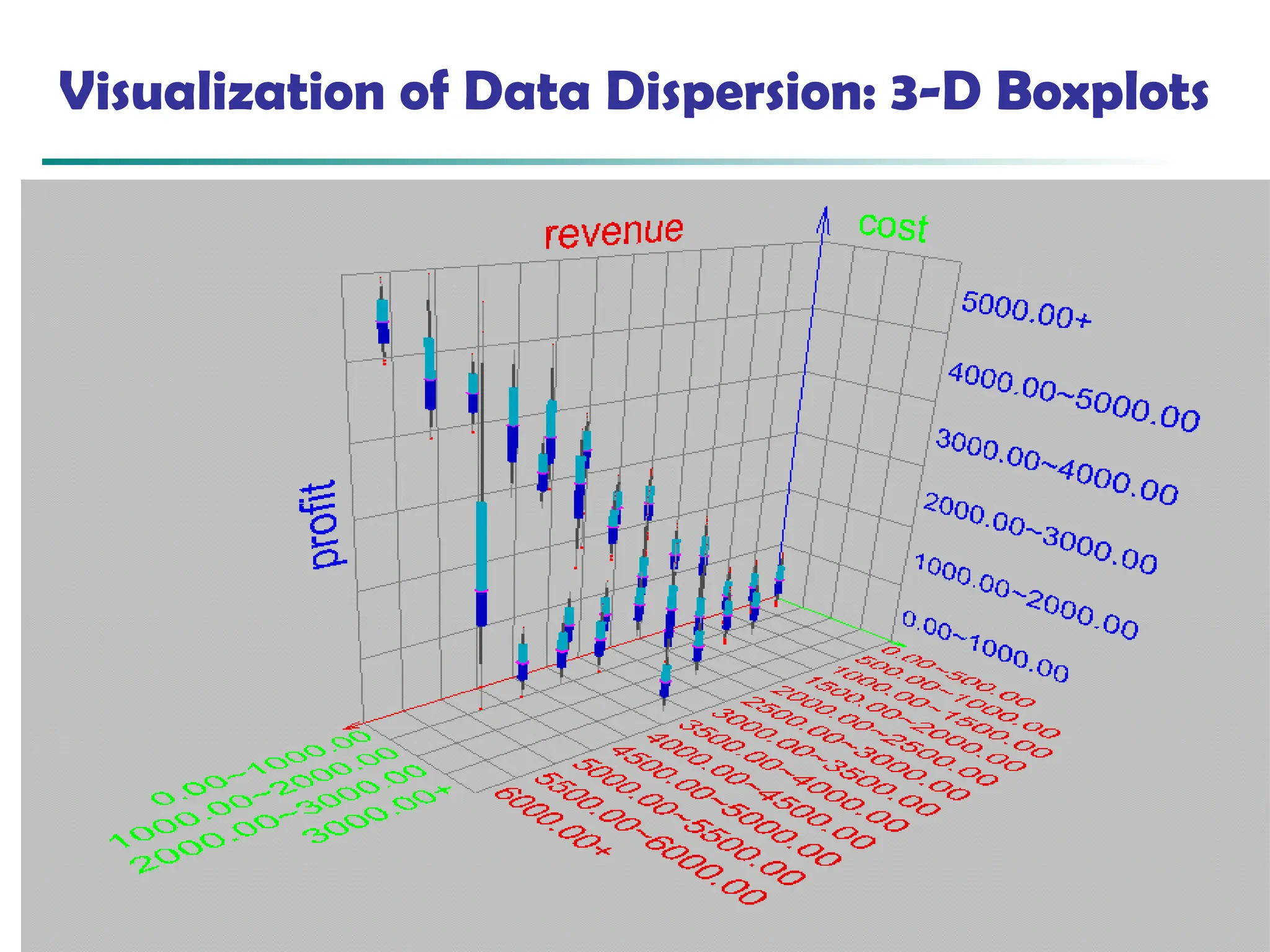



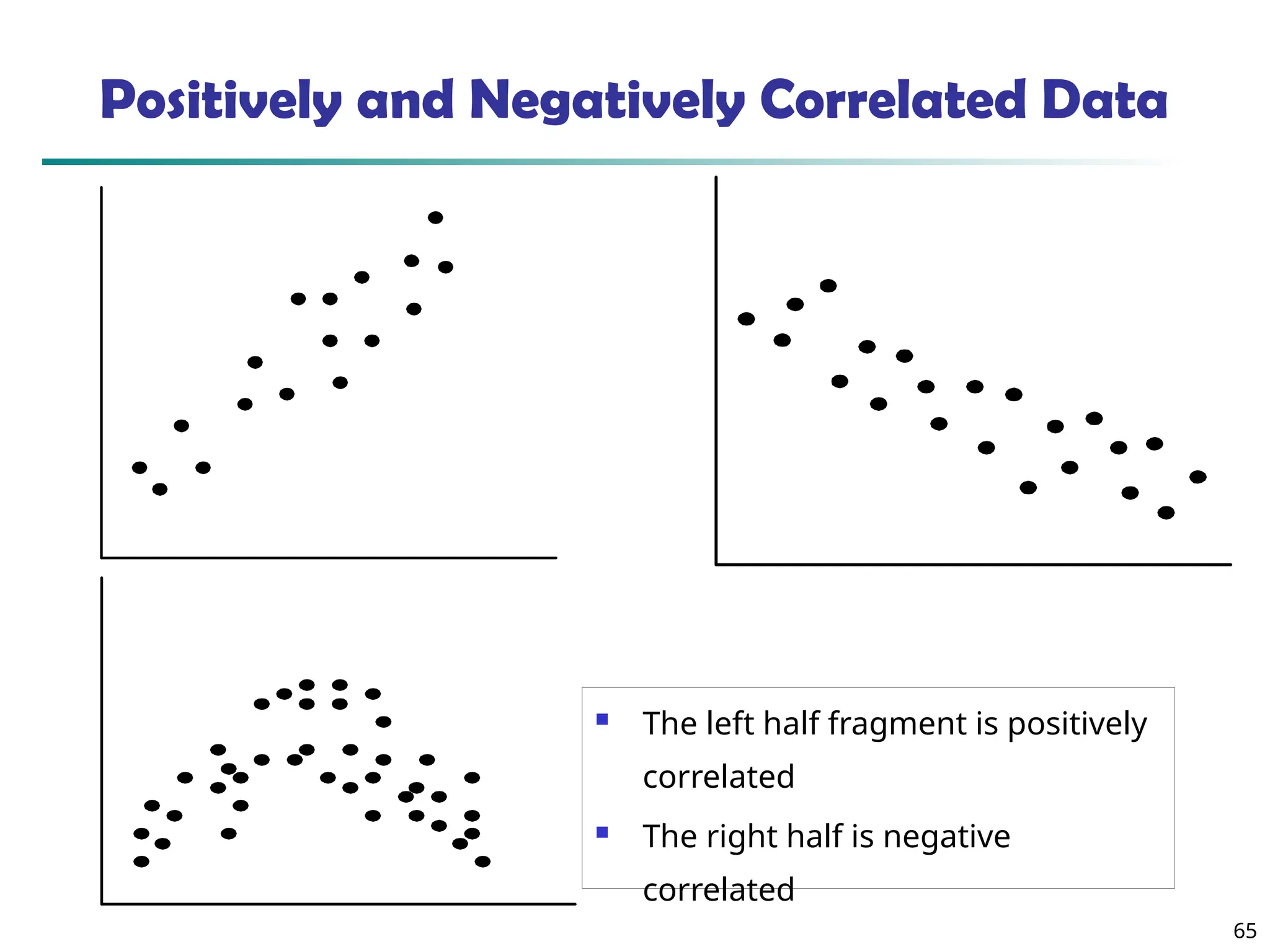
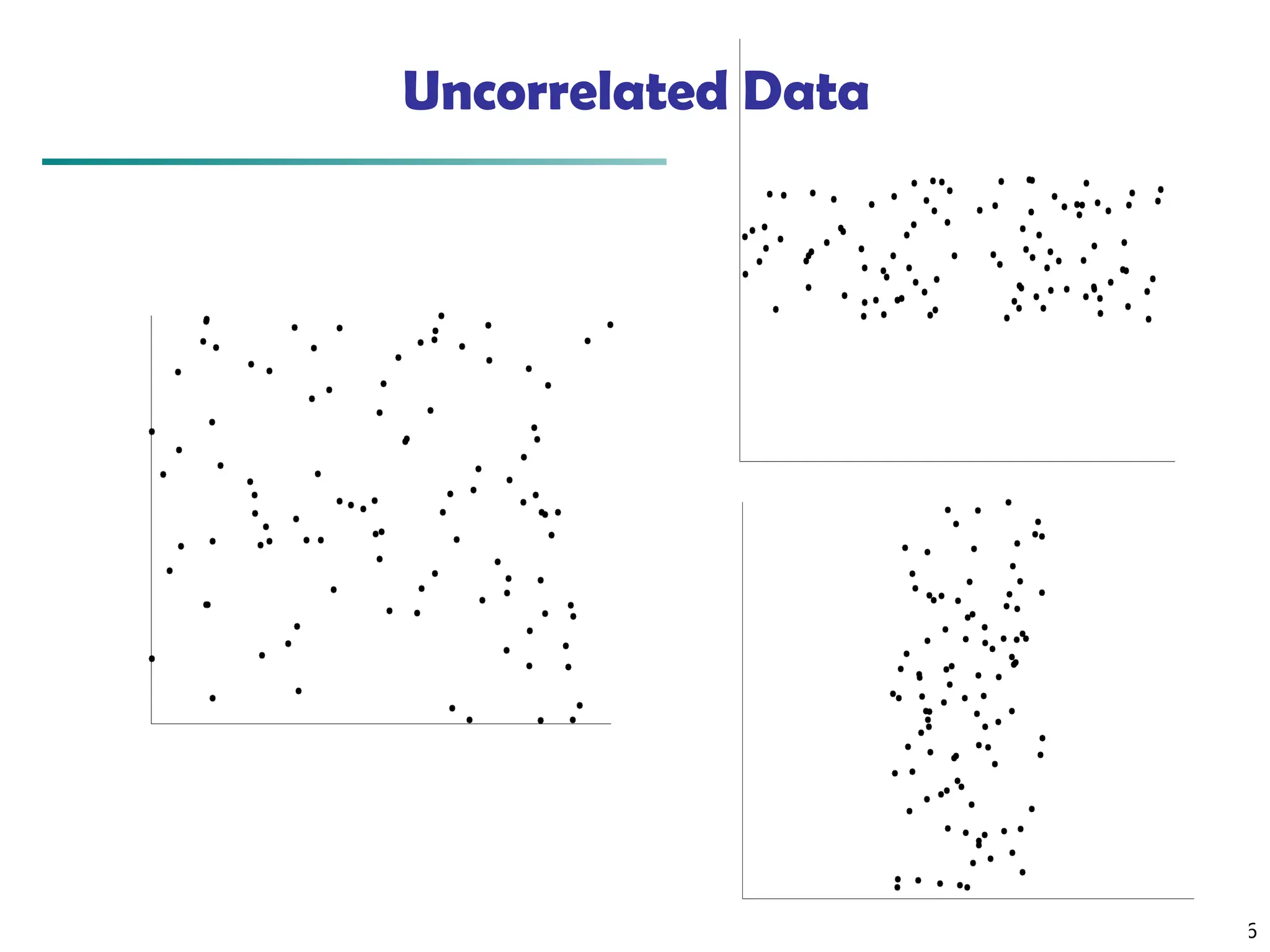


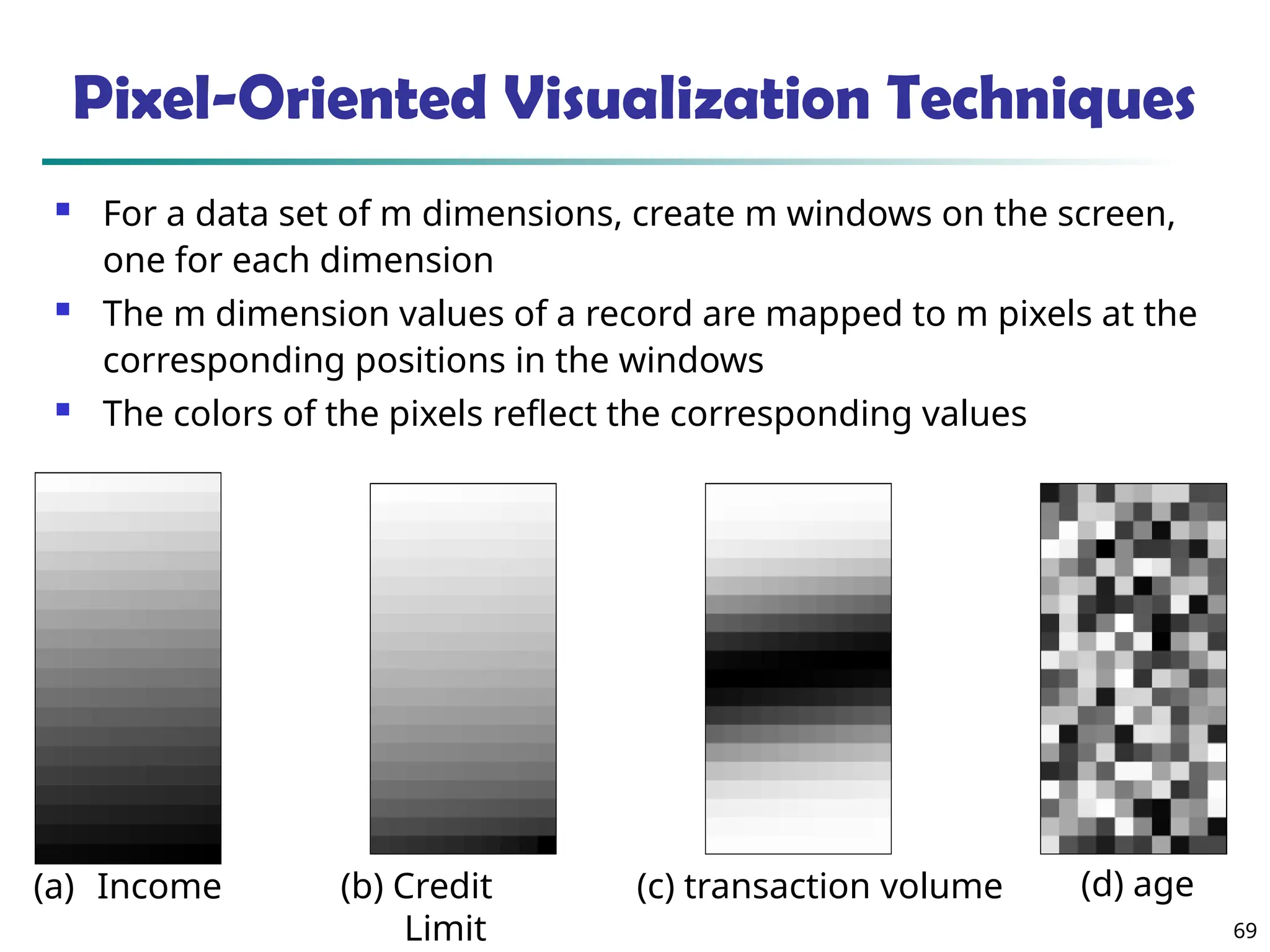

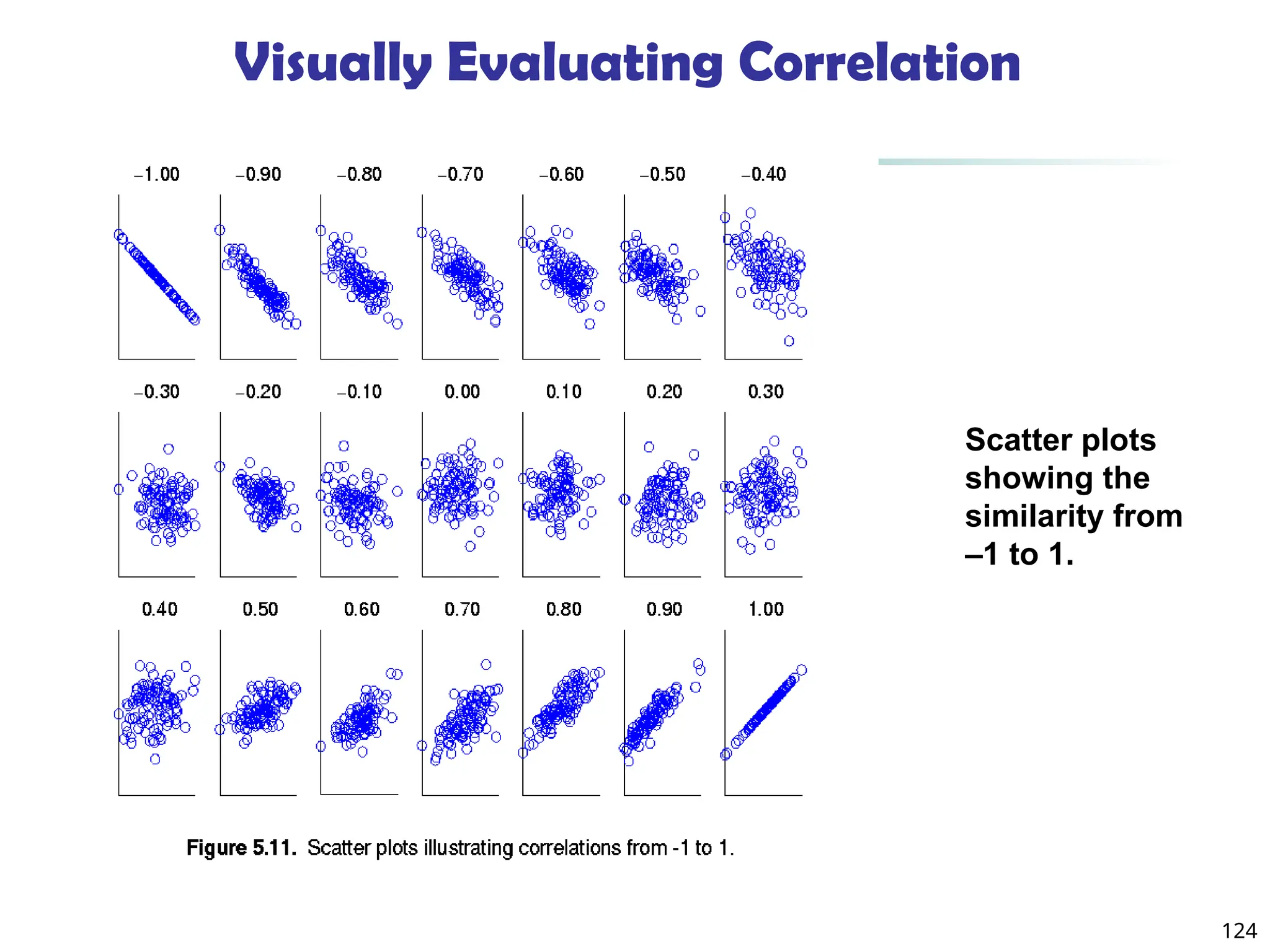
![73
Scatterplot Matrices
Matrix of scatterplots (x-y-diagrams) of the k-dim. data [total of (k2/2-k) scatterplots]
Used
by
ermission
of
M.
Ward,
Worcester
Polytechnic
Institute](https://image.slidesharecdn.com/dwdm3rdeditiontextbookslides-241024155956-ed696a42/75/DWDM-3rd-EDITION-TEXT-BOOK-SLIDES24-pptx-73-2048.jpg)

![75
Attr. 1 Attr. 2 Attr. k
Attr. 3
• • •
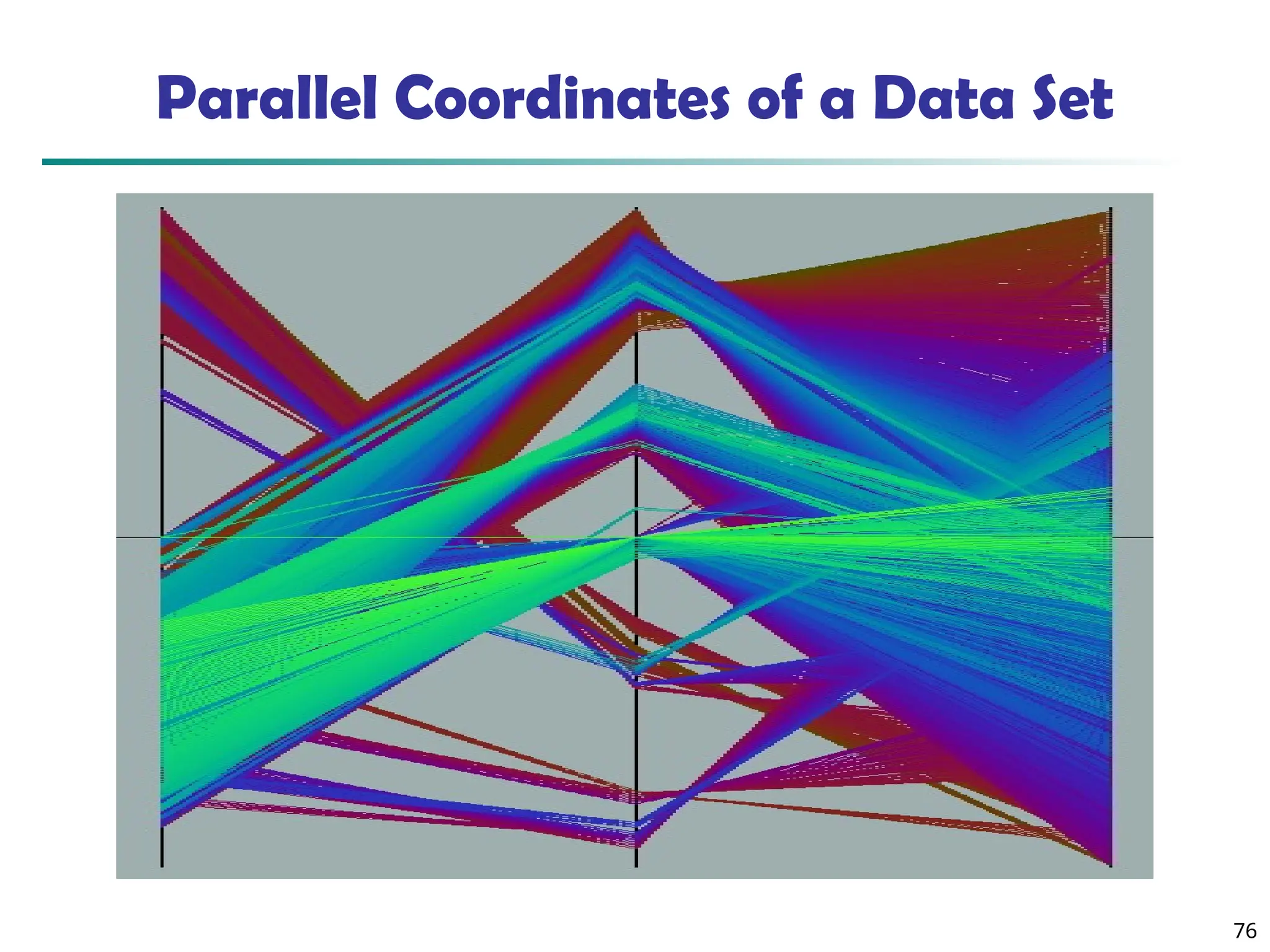
Parallel Coordinates
n equidistant axes which are parallel to one of the screen axes and
correspond to the attributes
The axes are scaled to the [minimum, maximum]: range of the
corresponding attribute
Every data item corresponds to a polygonal line which intersects
each of the axes at the point which corresponds to the value for
the attribute](https://image.slidesharecdn.com/dwdm3rdeditiontextbookslides-241024155956-ed696a42/75/DWDM-3rd-EDITION-TEXT-BOOK-SLIDES24-pptx-75-2048.jpg)





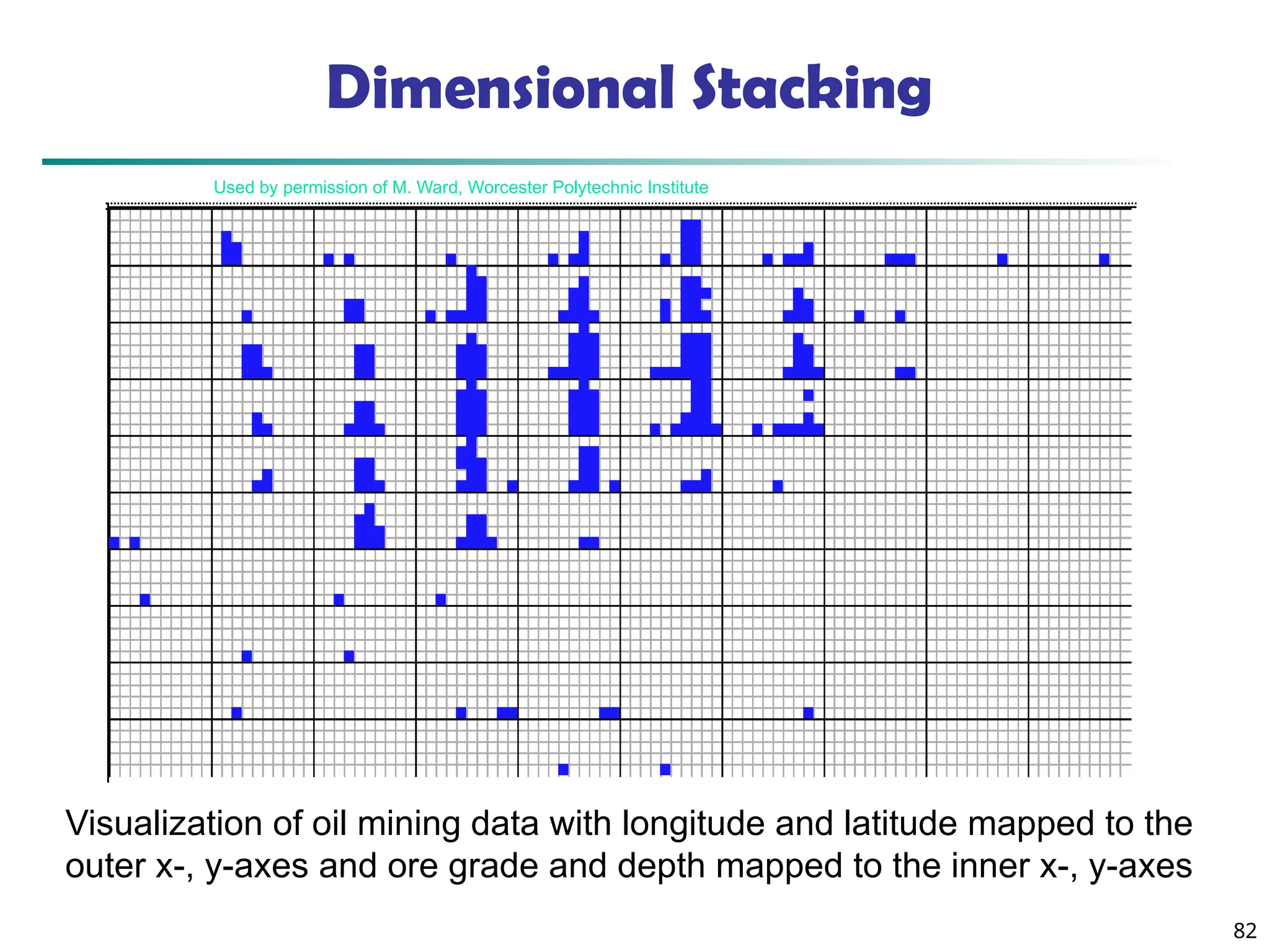





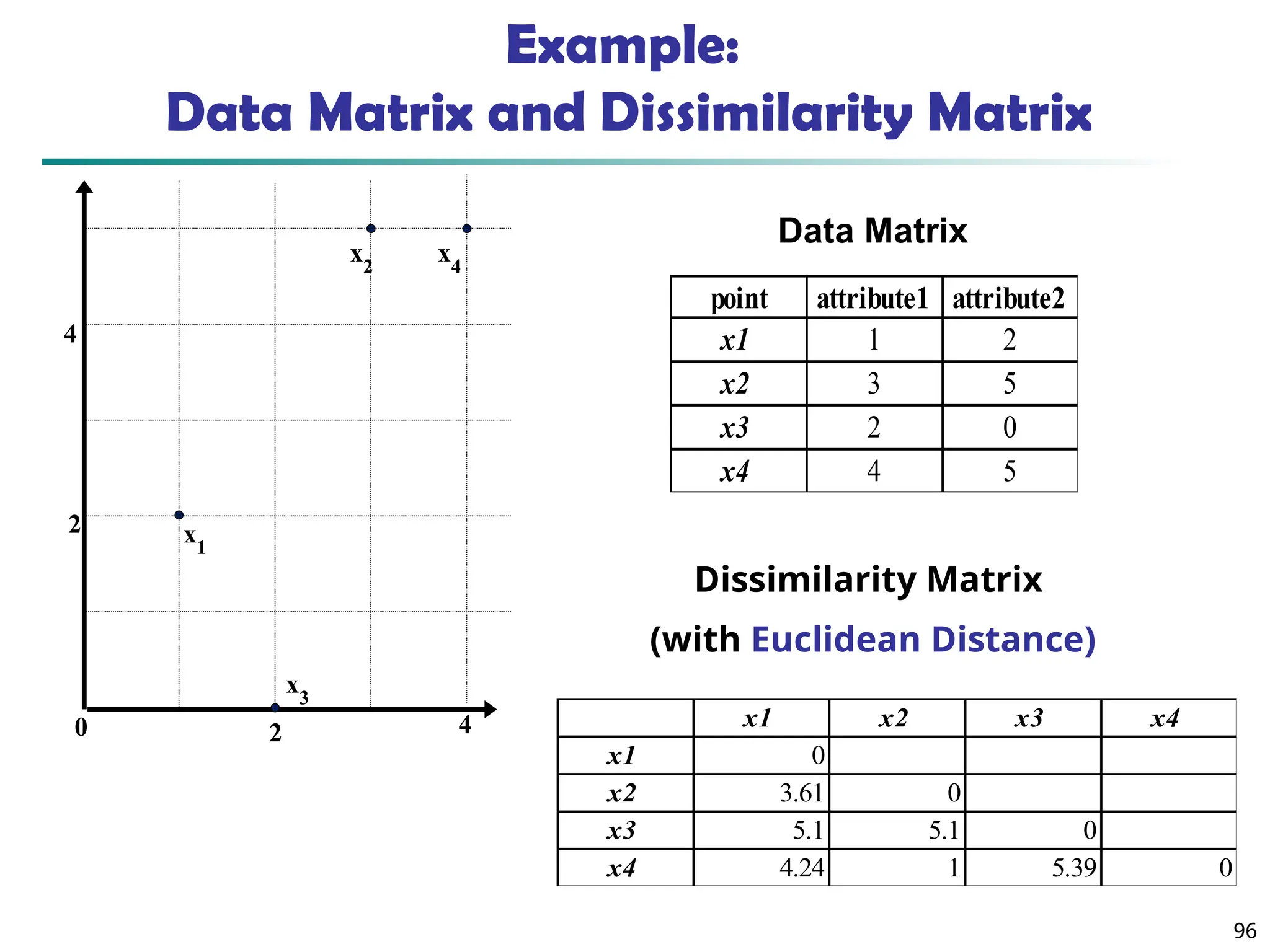
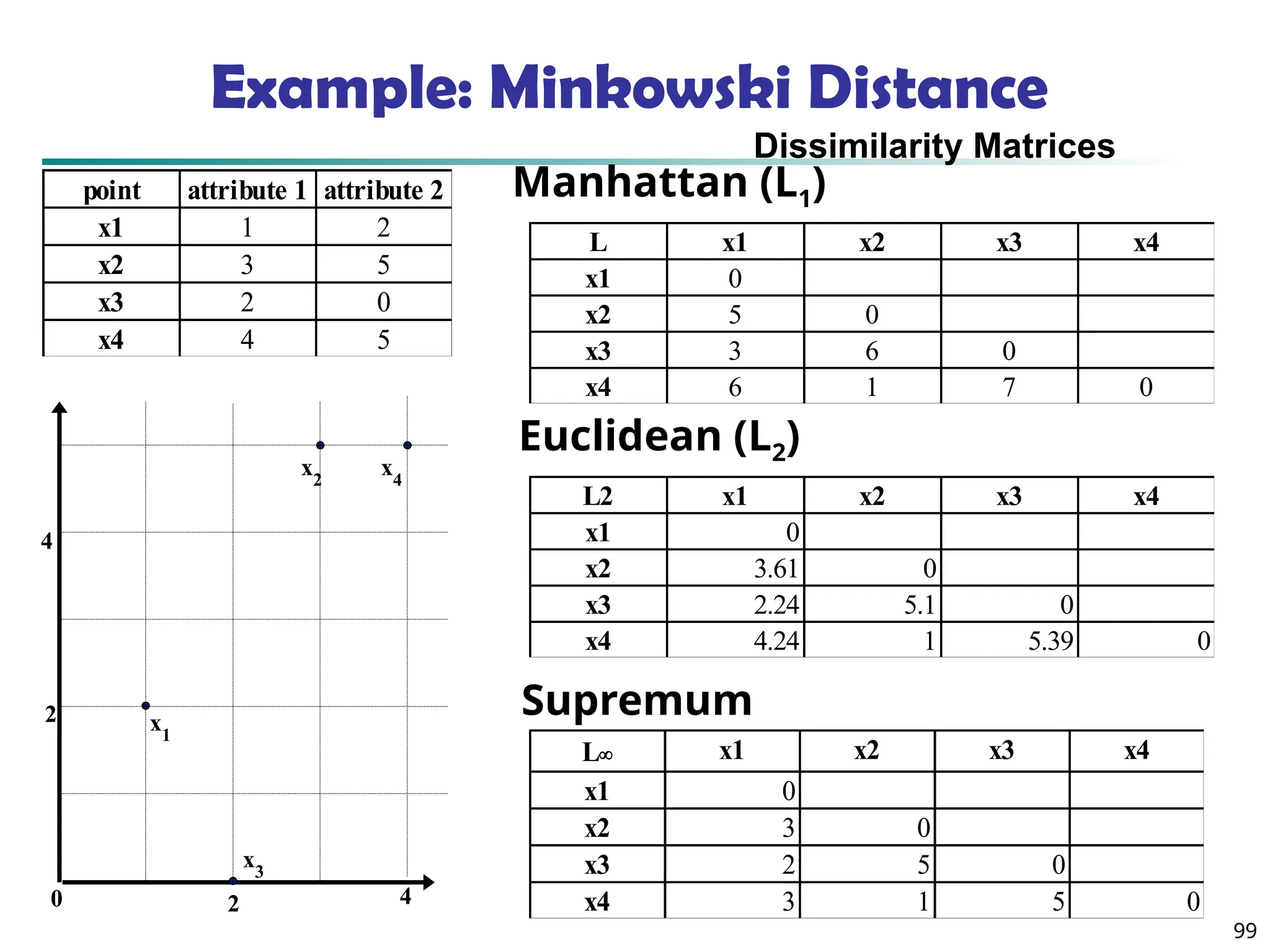
![90
Similarity and Dissimilarity
Similarity
Numerical measure of how alike two data objects are
Value is higher when objects are more alike
Often falls in the range [0,1]
Dissimilarity (e.g., distance)
Numerical measure of how different two data
objects are
Lower when objects are more alike
Minimum dissimilarity is often 0
Upper limit varies
Proximity refers to a similarity or dissimilarity](https://image.slidesharecdn.com/dwdm3rdeditiontextbookslides-241024155956-ed696a42/75/DWDM-3rd-EDITION-TEXT-BOOK-SLIDES24-pptx-90-2048.jpg)







![100
Ordinal Variables
An ordinal variable can be discrete or continuous
Order is important, e.g., rank
Can be treated like interval-scaled
replace xif by their rank
map the range of each variable onto [0, 1] by
replacing i-th object in the f-th variable by
compute the dissimilarity using methods for
interval-scaled variables
1
1
f
if
if M
r
z
}
,...,
1
{ f
if
M
r ](https://image.slidesharecdn.com/dwdm3rdeditiontextbookslides-241024155956-ed696a42/75/DWDM-3rd-EDITION-TEXT-BOOK-SLIDES24-pptx-100-2048.jpg)




























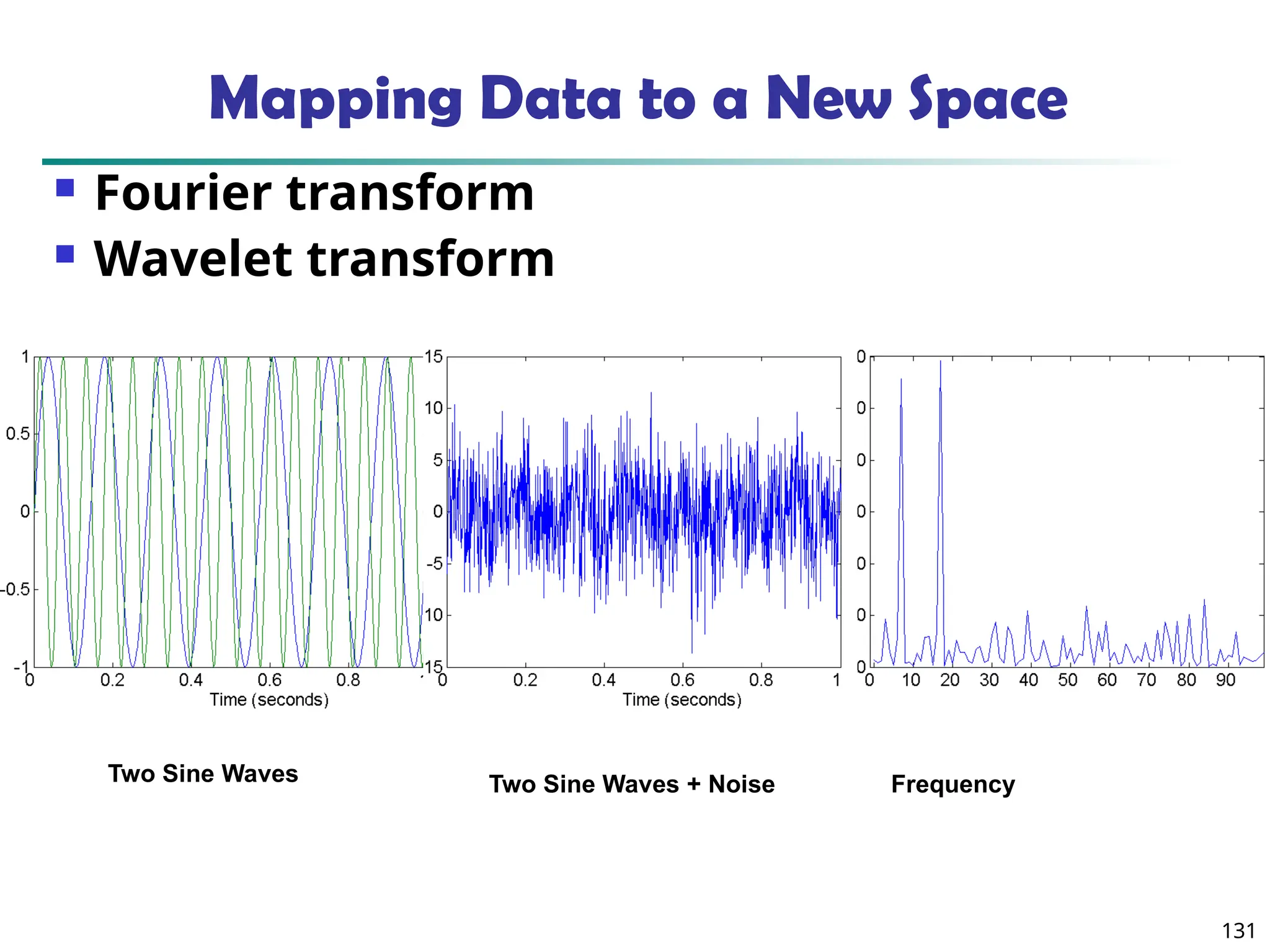


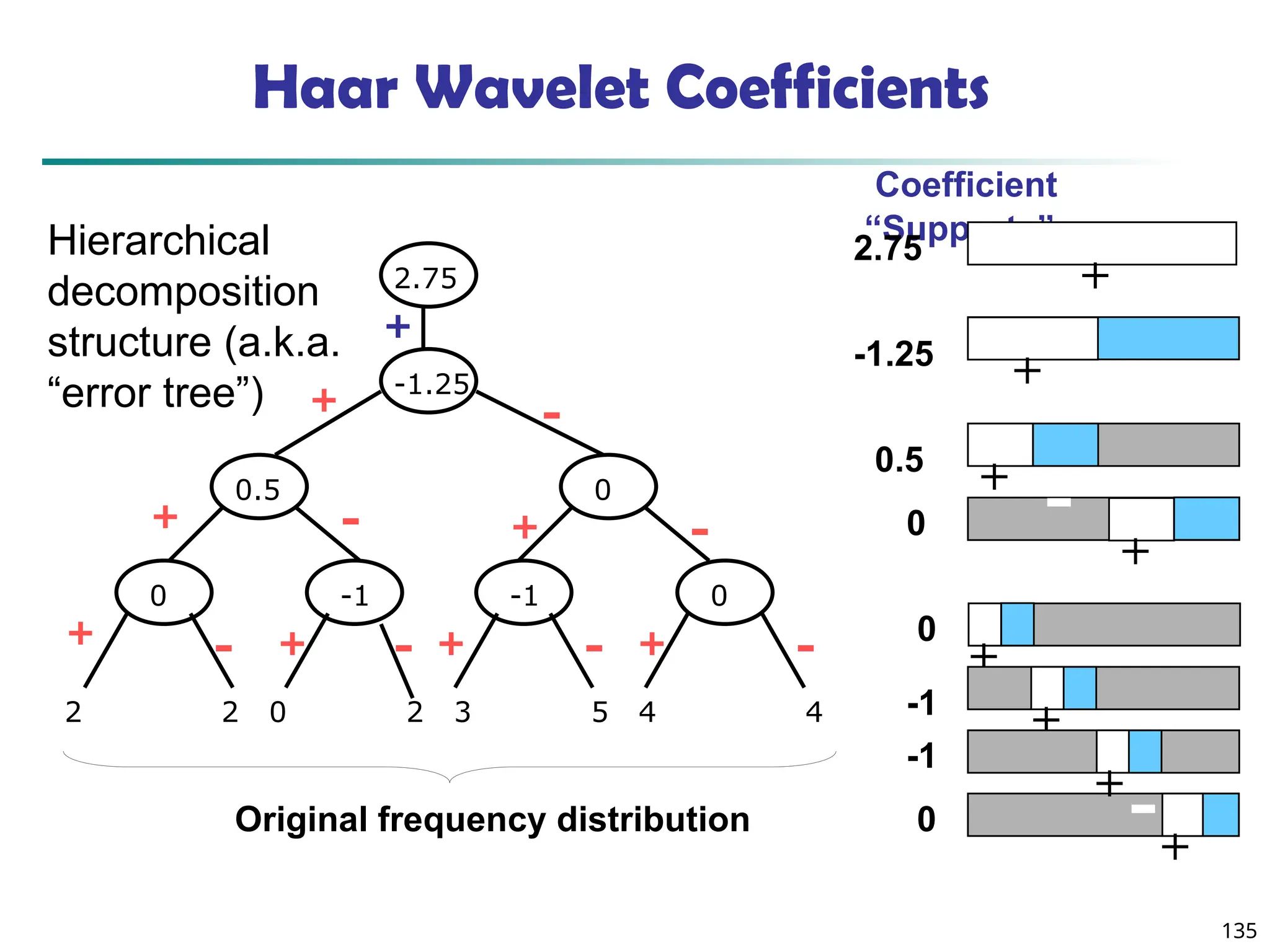
![134
Wavelet Decomposition
Wavelets: A math tool for space-efficient hierarchical
decomposition of functions
S = [2, 2, 0, 2, 3, 5, 4, 4] can be transformed to S^ = [23
/4,
-11
/4, 1
/2, 0, 0, -1, -1, 0]
Compression: many small detail coefficients can be
replaced by 0’s, and only the significant coefficients
are retained](https://image.slidesharecdn.com/dwdm3rdeditiontextbookslides-241024155956-ed696a42/75/DWDM-3rd-EDITION-TEXT-BOOK-SLIDES24-pptx-134-2048.jpg)

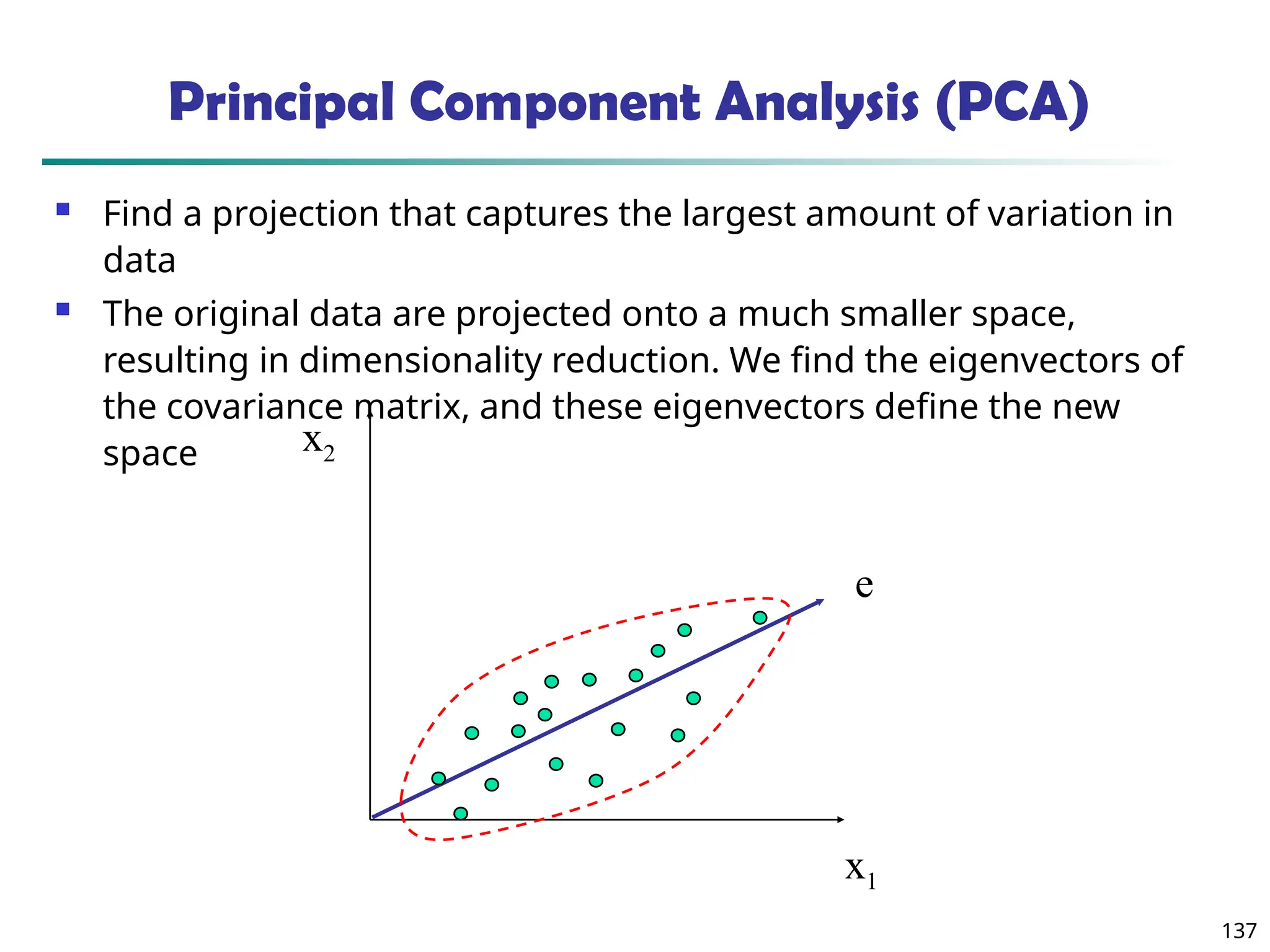








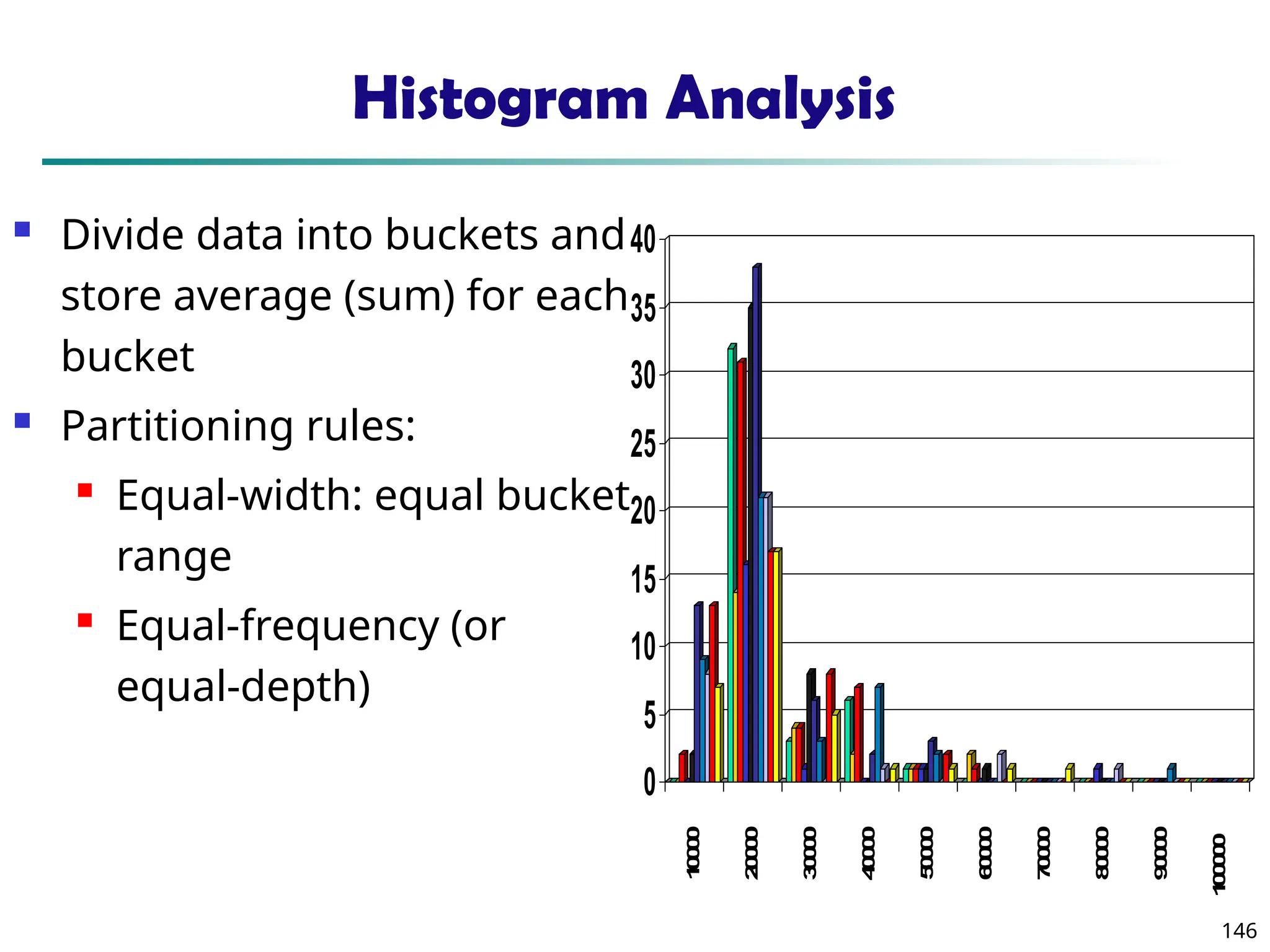



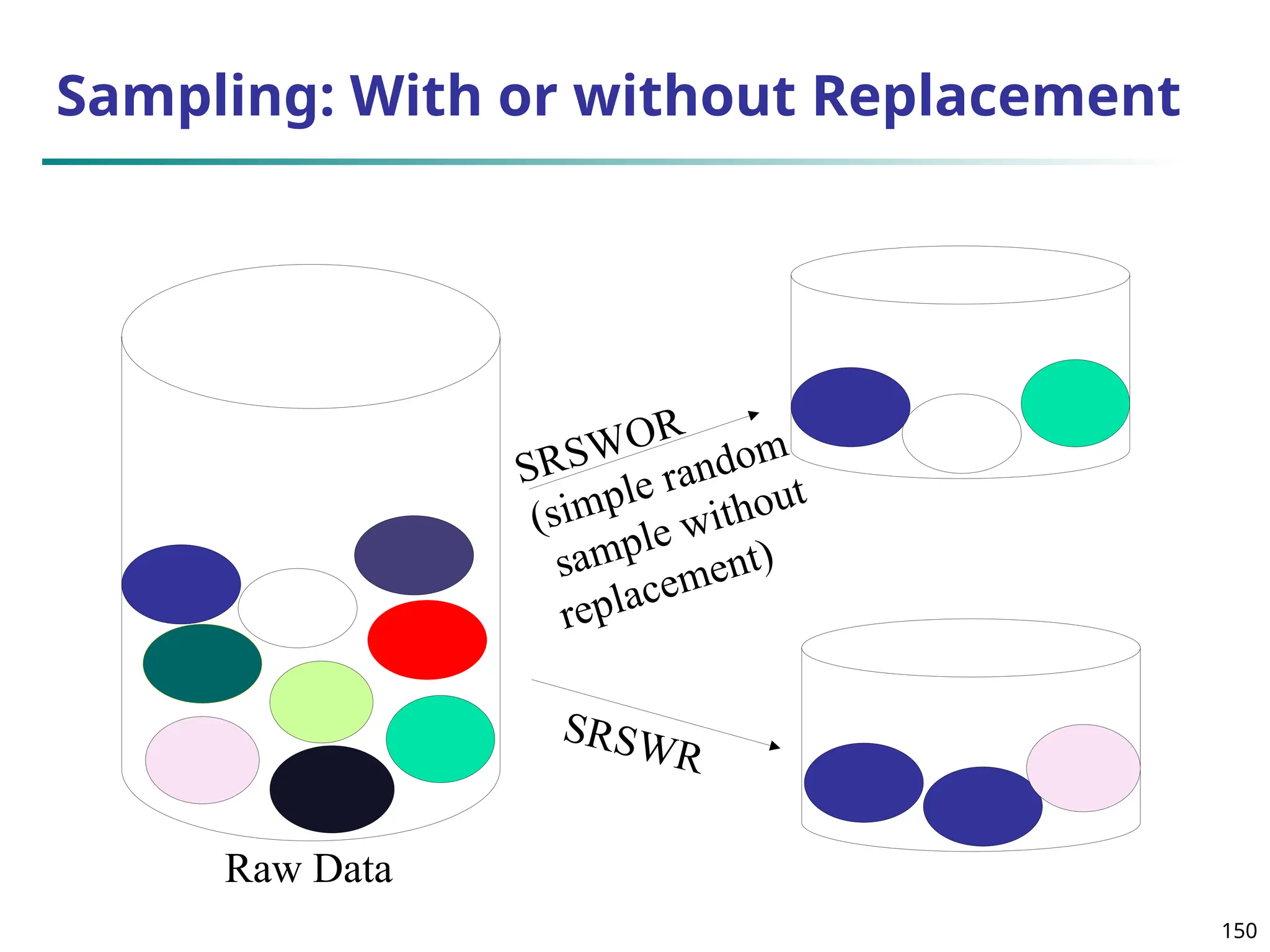
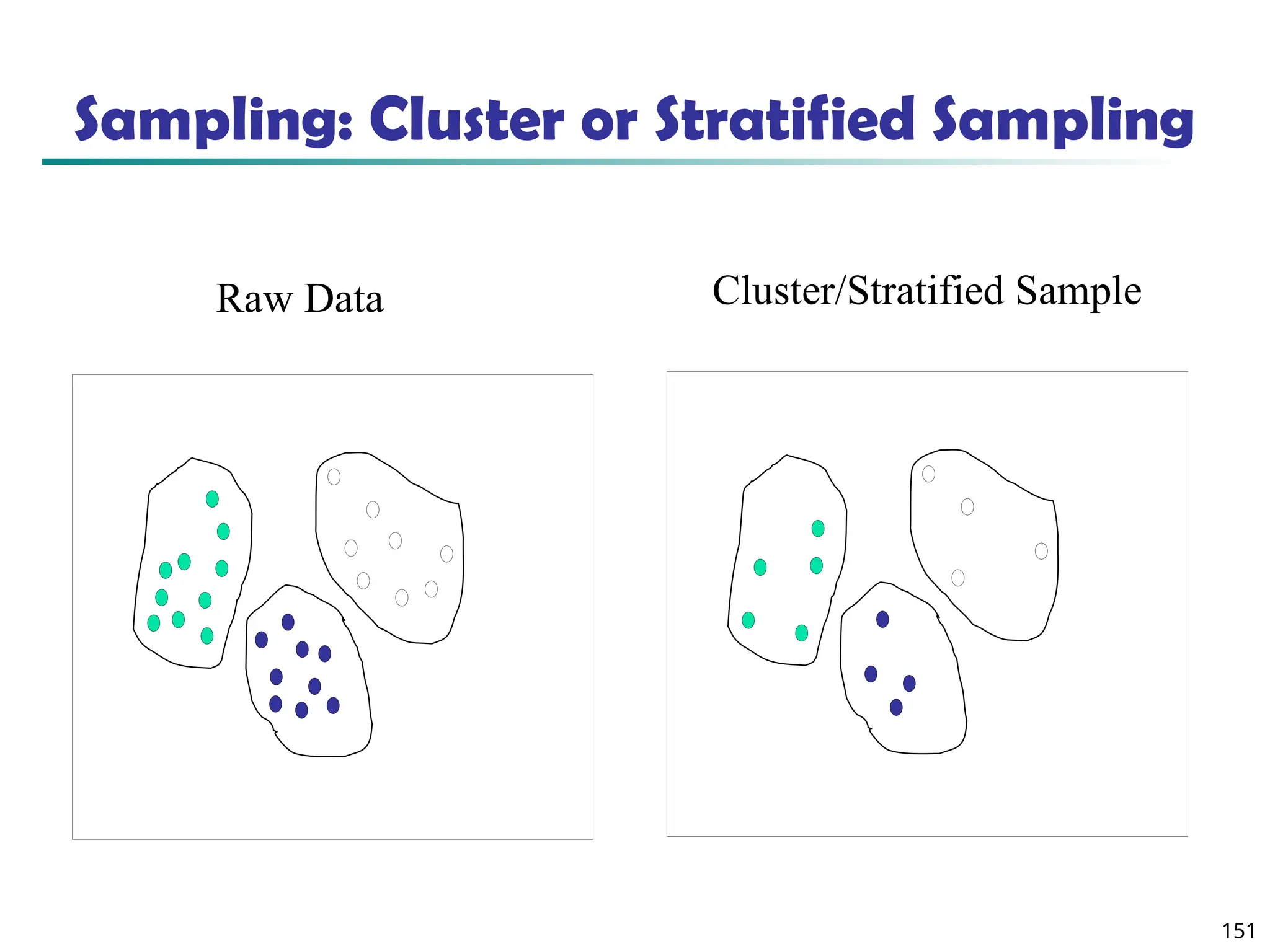


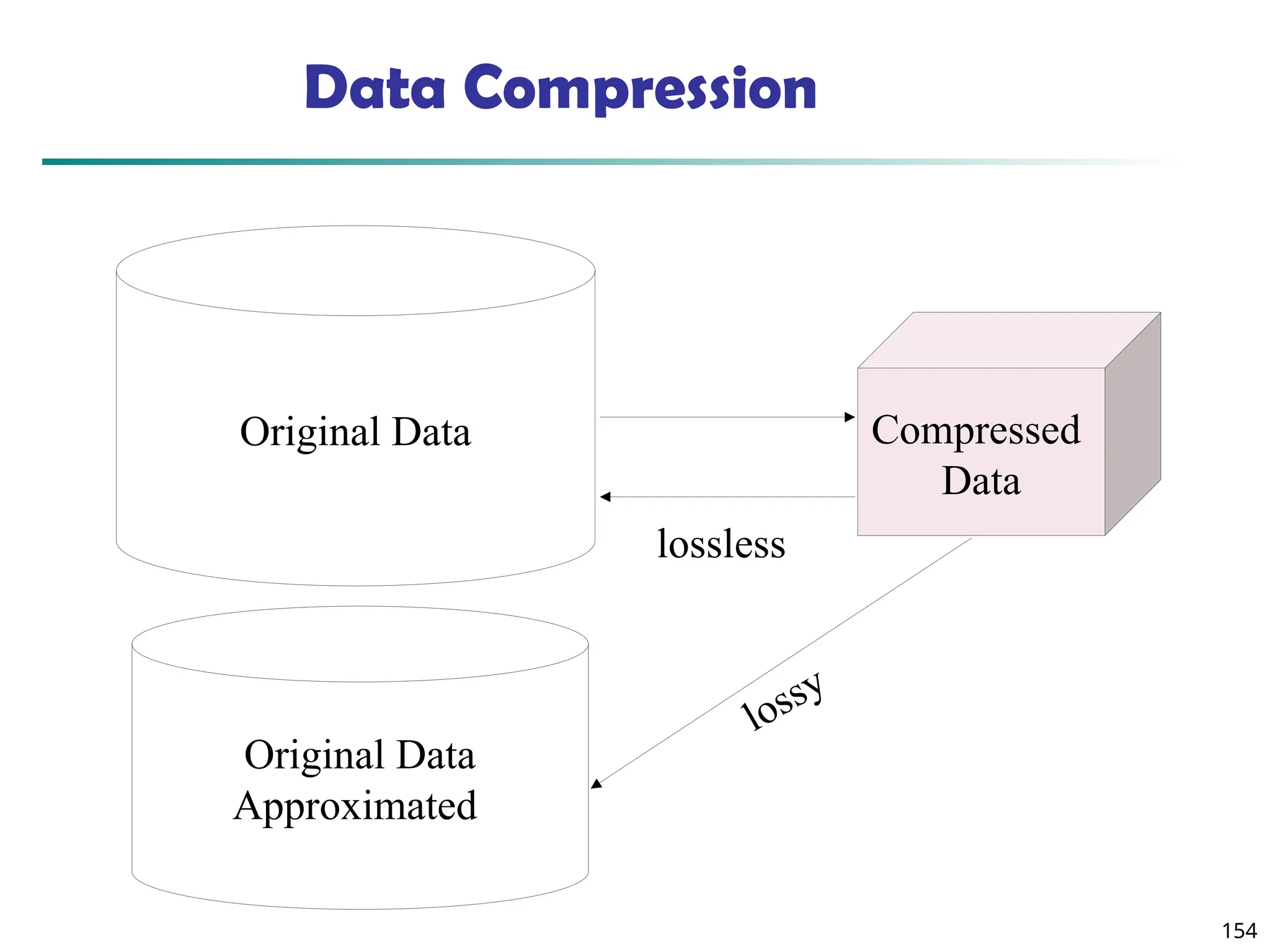


![157
Normalization
Min-max normalization: to [new_minA, new_maxA]
Ex. Let income range $12,000 to $98,000 normalized to [0.0,
1.0]. Then $73,000 is mapped to
Z-score normalization (μ: mean, σ: standard deviation):
Ex. Let μ = 54,000, σ = 16,000. Then
Normalization by decimal scaling
716
.
0
0
)
0
0
.
1
(
000
,
12
000
,
98
000
,
12
600
,
73
A
A
A
A
A
A
min
new
min
new
max
new
min
max
min
v
v _
)
_
_
(
'
A
A
v
v
'
j
v
v
10
' Where j is the smallest integer such that Max(|ν’|) < 1
225
.
1
000
,
16
000
,
54
600
,
73
](https://image.slidesharecdn.com/dwdm3rdeditiontextbookslides-241024155956-ed696a42/75/DWDM-3rd-EDITION-TEXT-BOOK-SLIDES24-pptx-157-2048.jpg)




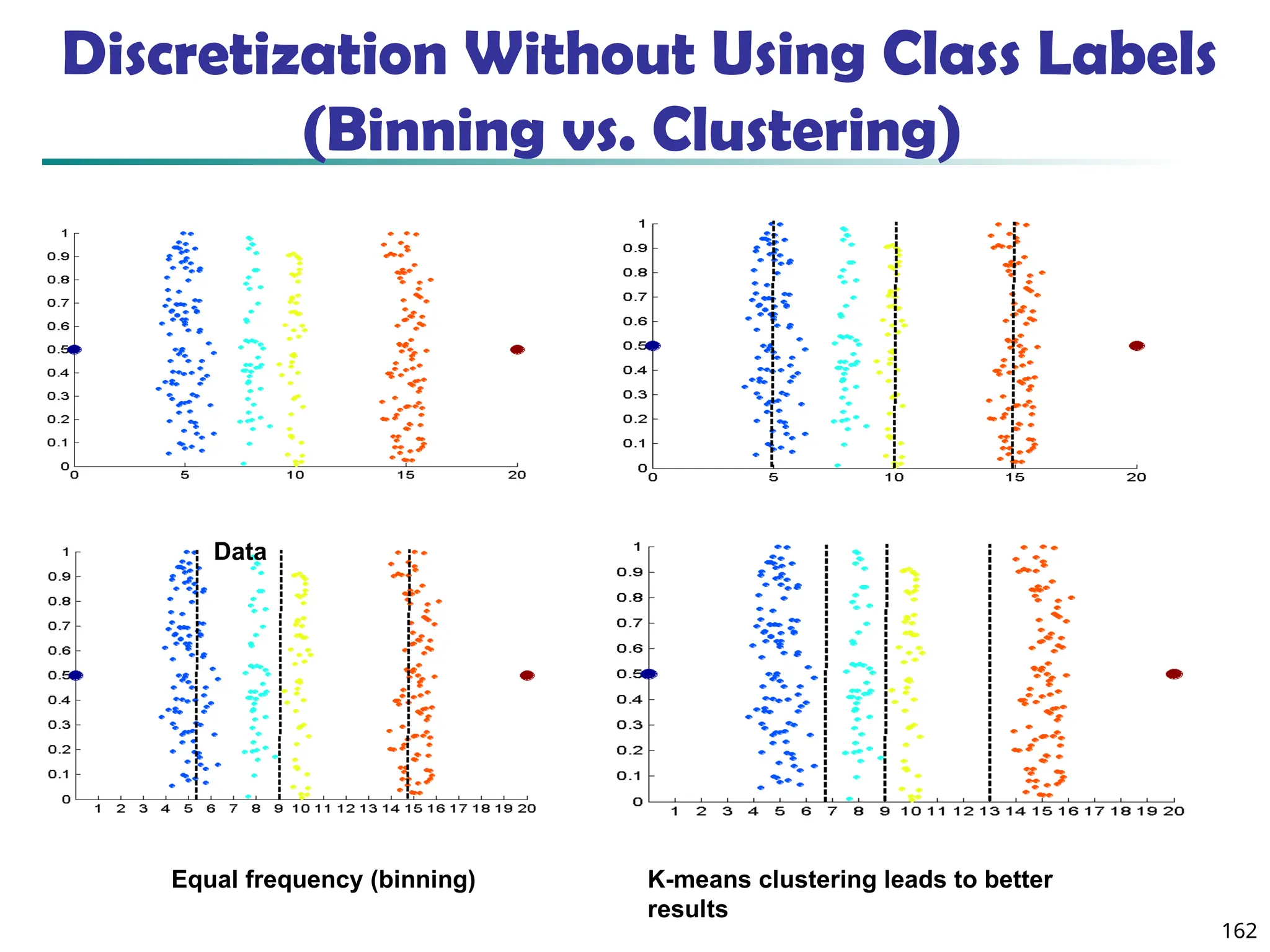














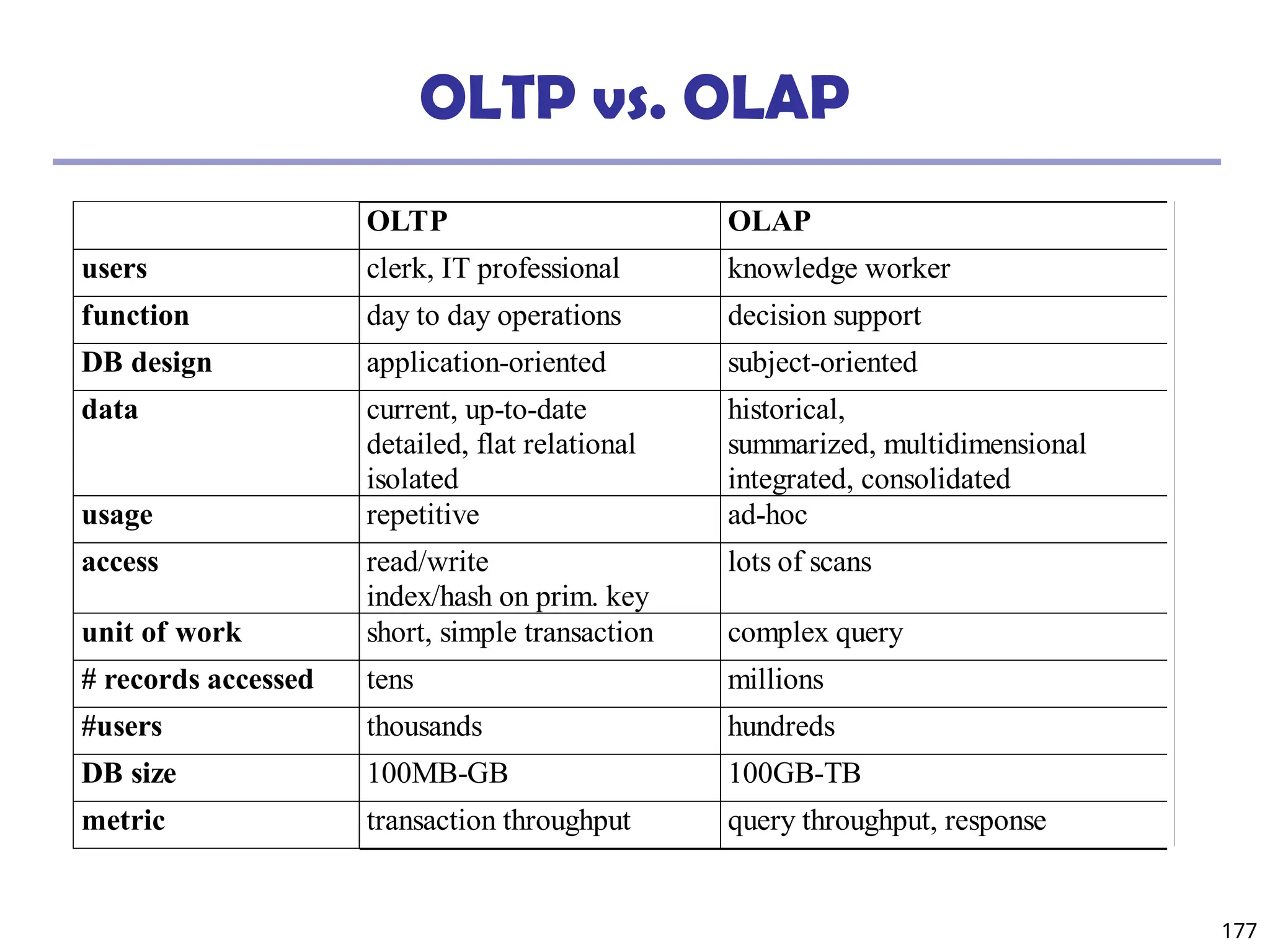

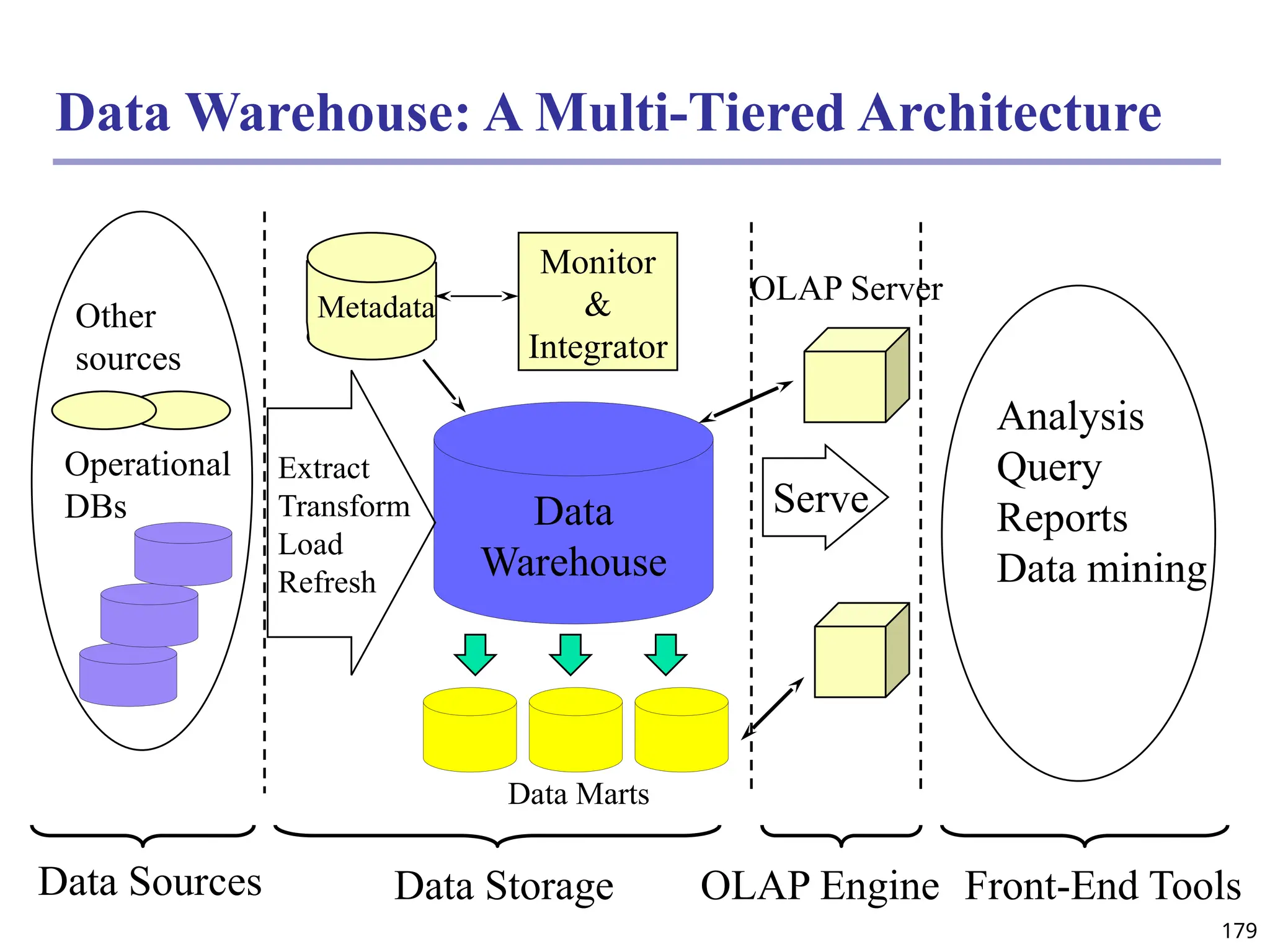






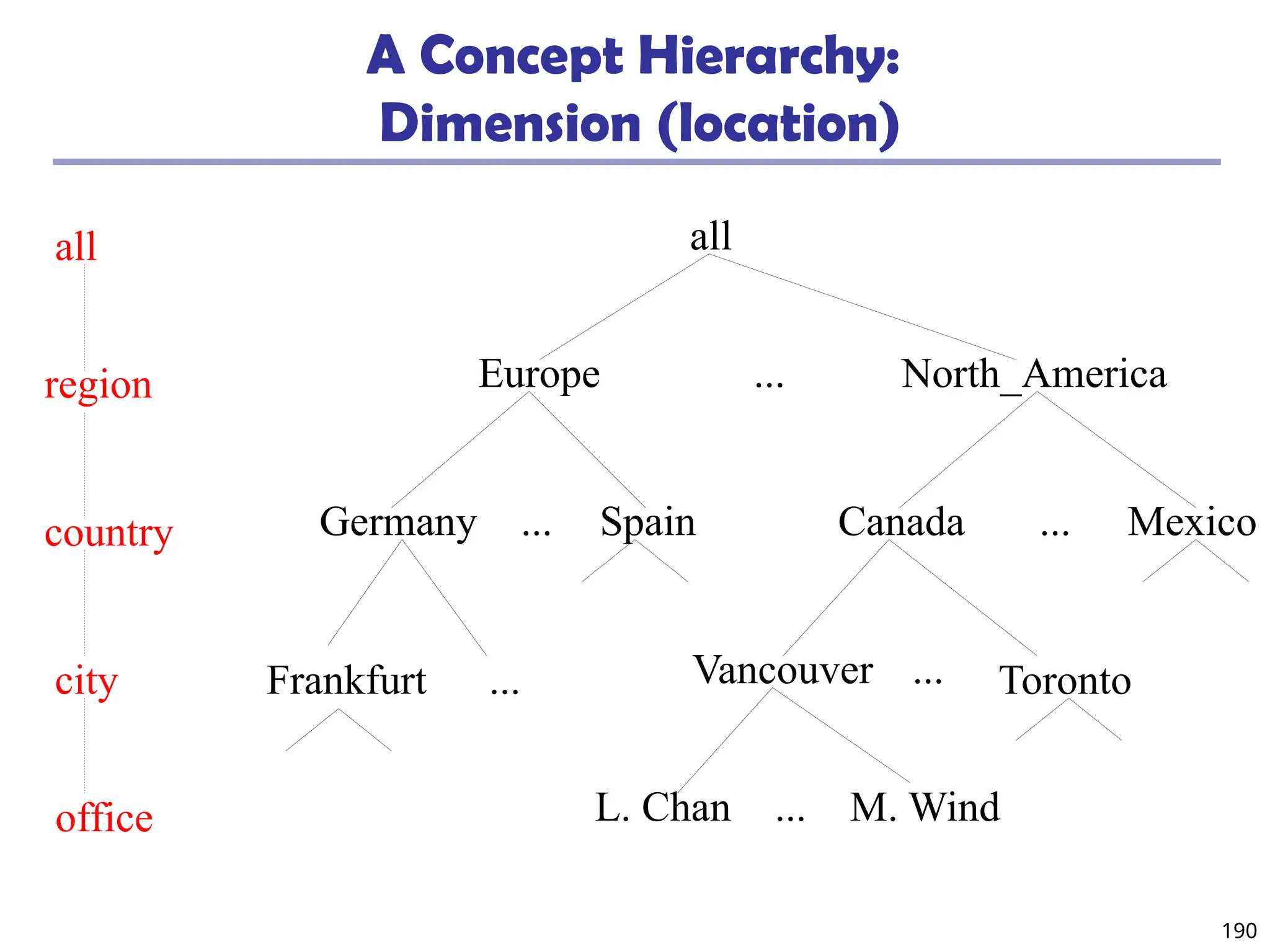



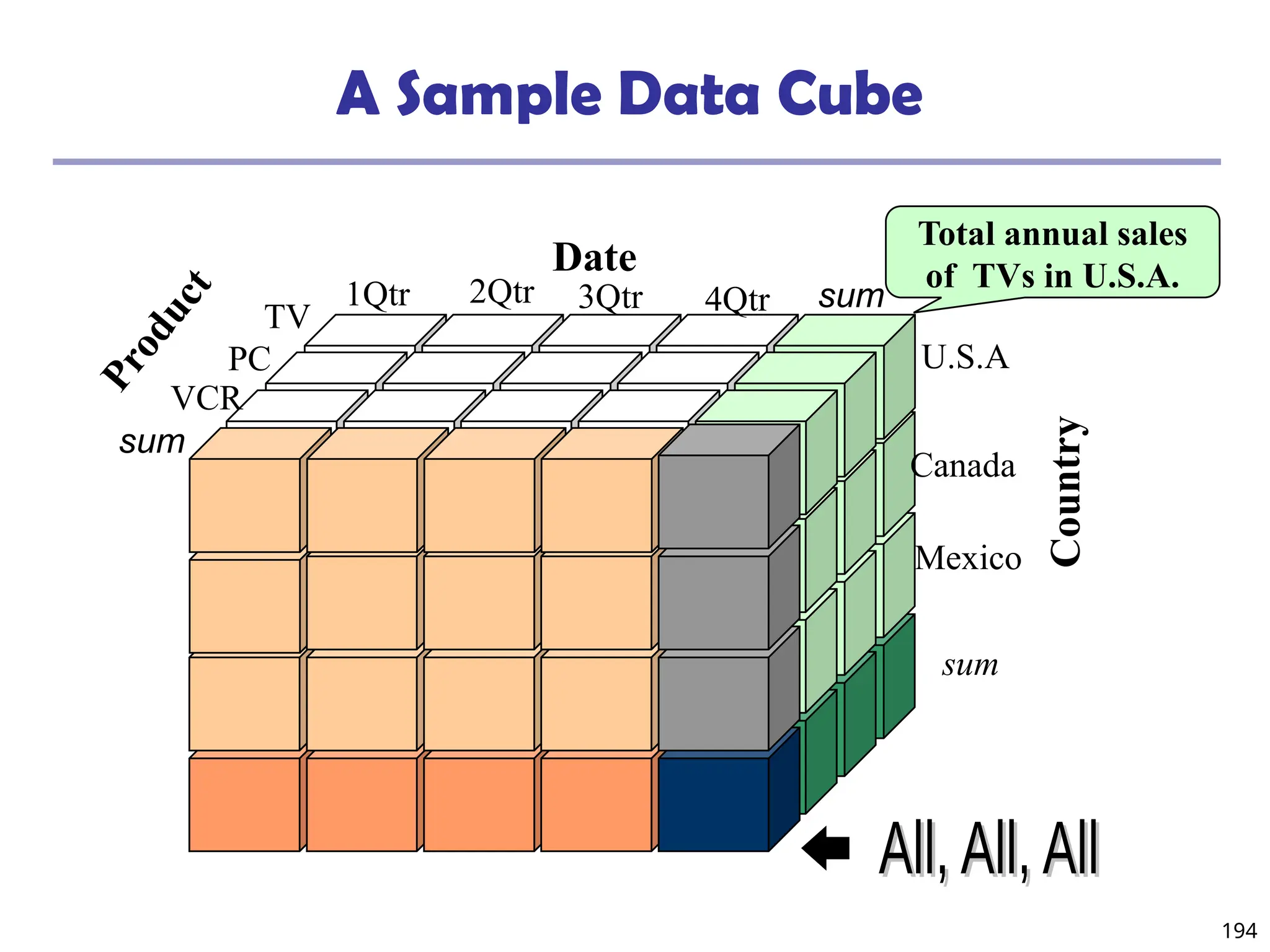


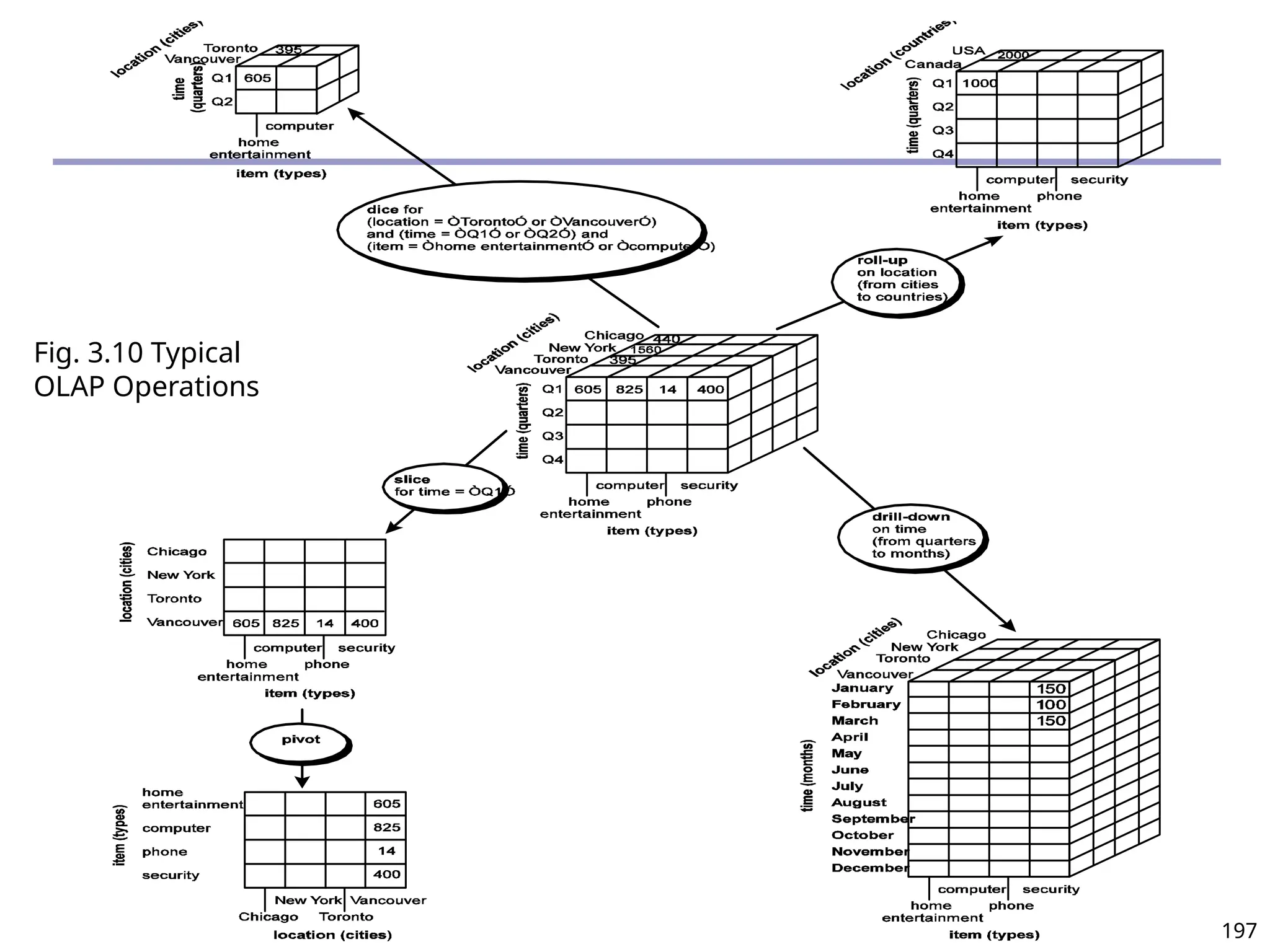
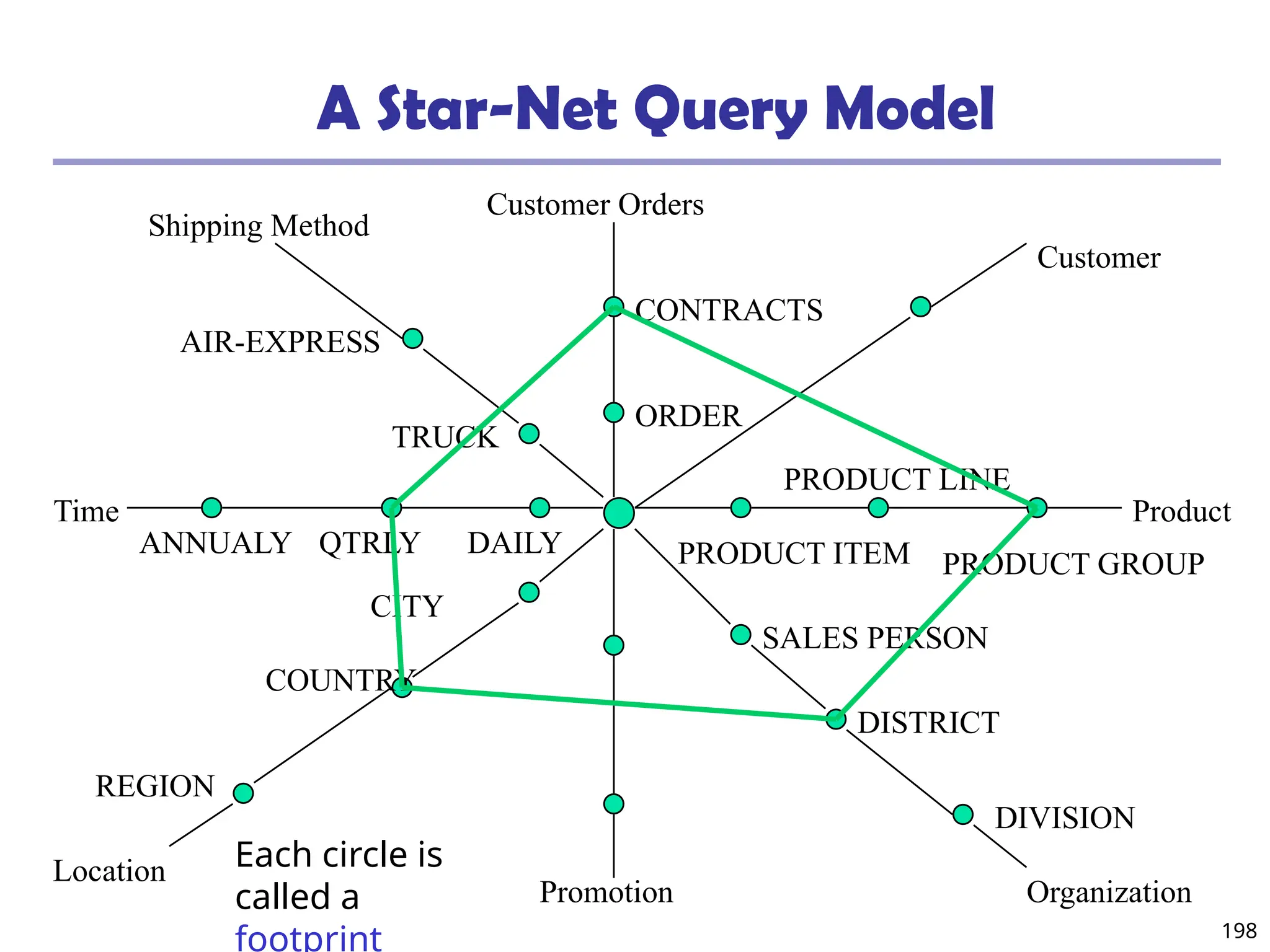






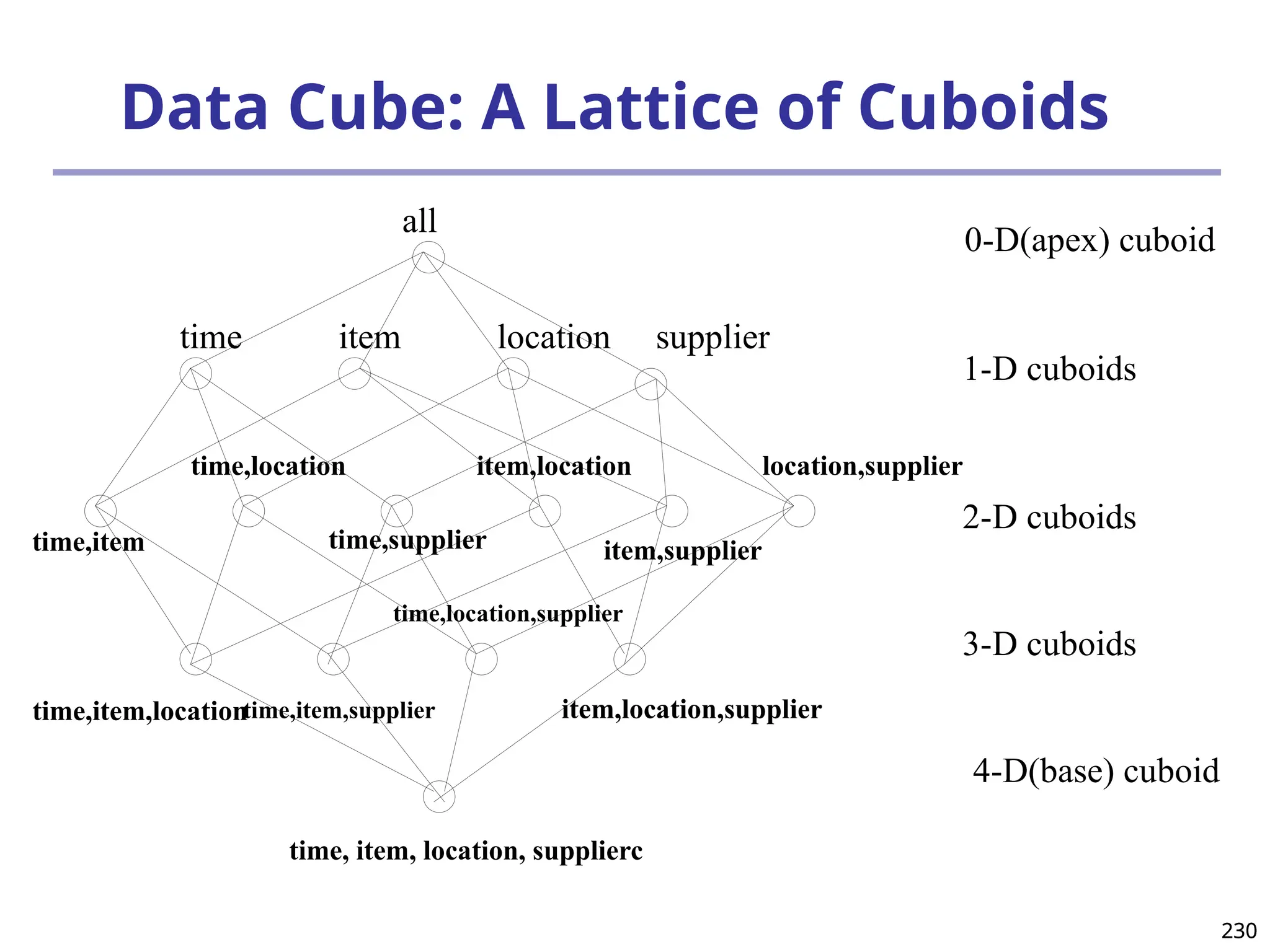
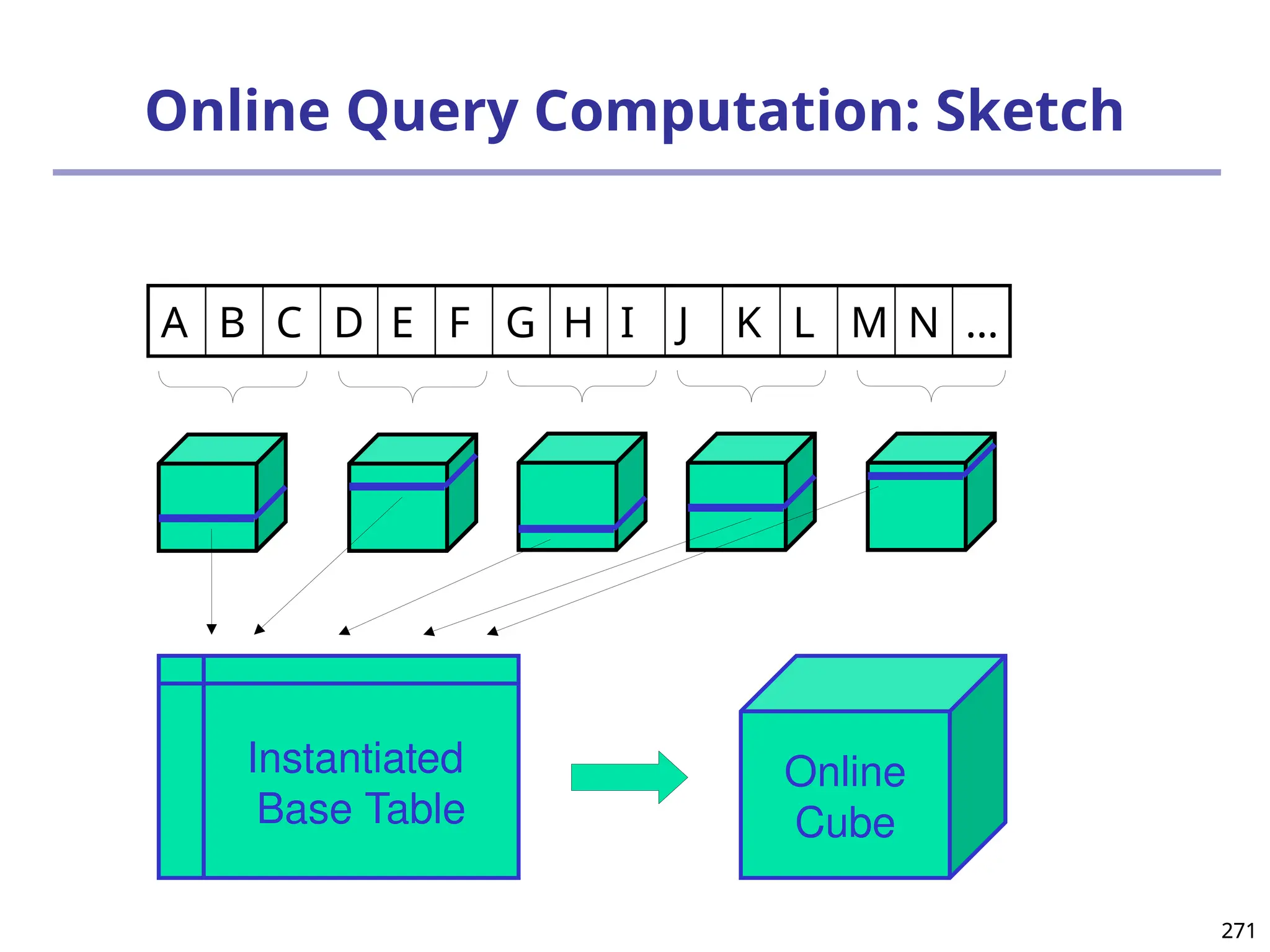
![208
The “Compute Cube” Operator
Cube definition and computation in DMQL
define cube sales [item, city, year]: sum (sales_in_dollars)
compute cube sales
Transform it into a SQL-like language (with a new operator
cube by, introduced by Gray et al.’96)
SELECT item, city, year, SUM (amount)
FROM SALES
CUBE BY item, city, year
Need compute the following Group-Bys
(date, product, customer),
(date,product),(date, customer), (product, customer),
(date), (product), (customer)
()
(item)
(city)
()
(year)
(city, item) (city, year) (item, year)
(city, item, year)](https://image.slidesharecdn.com/dwdm3rdeditiontextbookslides-241024155956-ed696a42/75/DWDM-3rd-EDITION-TEXT-BOOK-SLIDES24-pptx-208-2048.jpg)
![209
Indexing OLAP Data: Bitmap Index
Index on a particular column
Each value in the column has a bit vector: bit-op is fast
The length of the bit vector: # of records in the base table
The i-th bit is set if the i-th row of the base table has the value for
the indexed column
not suitable for high cardinality domains
A recent bit compression technique, Word-Aligned Hybrid (WAH),
makes it work for high cardinality domain as well [Wu, et al.
TODS’06]
Cust Region Type
C1 Asia Retail
C2 Europe Dealer
C3 Asia Dealer
C4 America Retail
C5 Europe Dealer
RecID Retail Dealer
1 1 0
2 0 1
3 0 1
4 1 0
5 0 1
RecIDAsia Europe America
1 1 0 0
2 0 1 0
3 1 0 0
4 0 0 1
5 0 1 0
Base table Index on Region Index on Type](https://image.slidesharecdn.com/dwdm3rdeditiontextbookslides-241024155956-ed696a42/75/DWDM-3rd-EDITION-TEXT-BOOK-SLIDES24-pptx-209-2048.jpg)








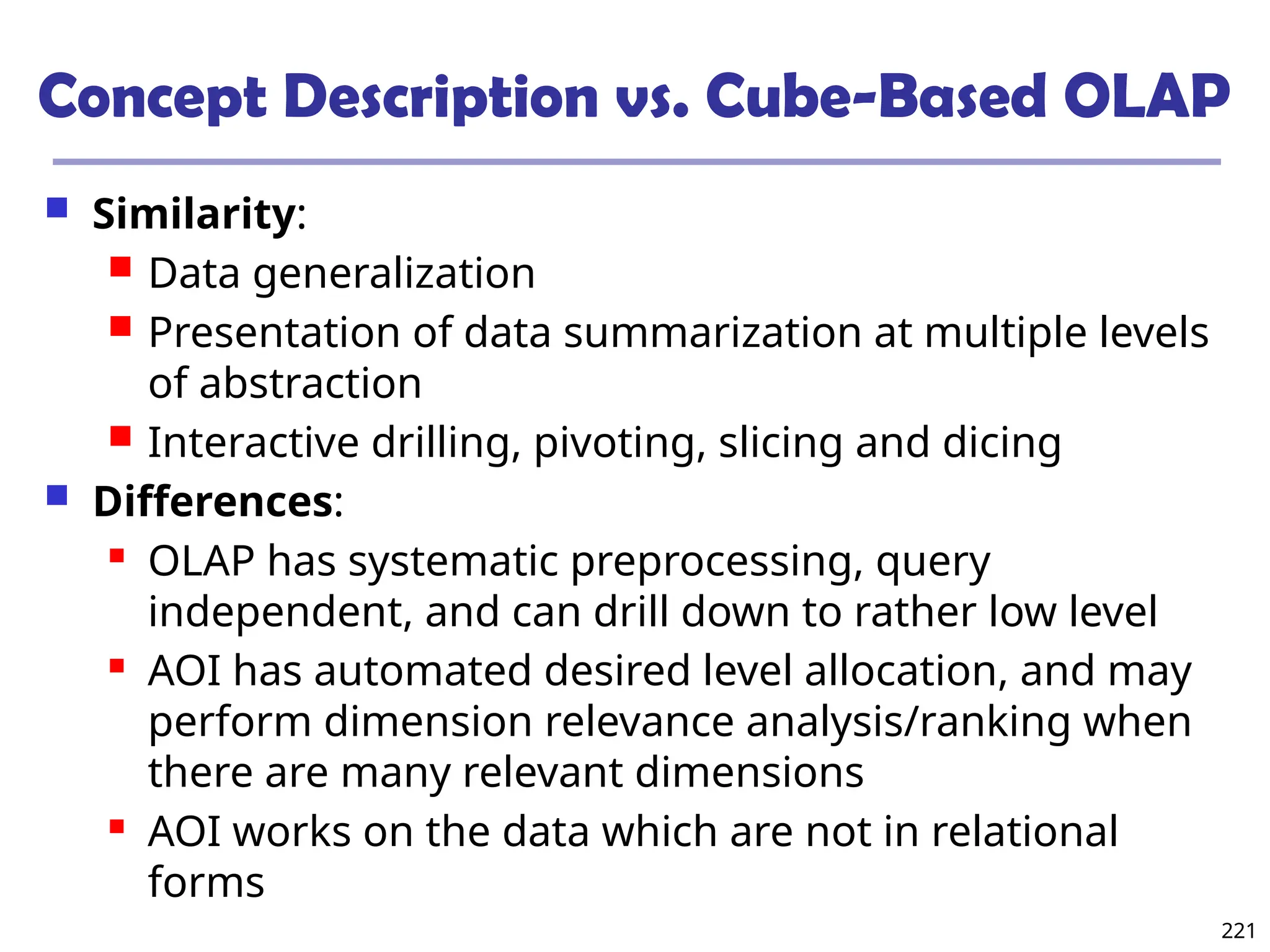
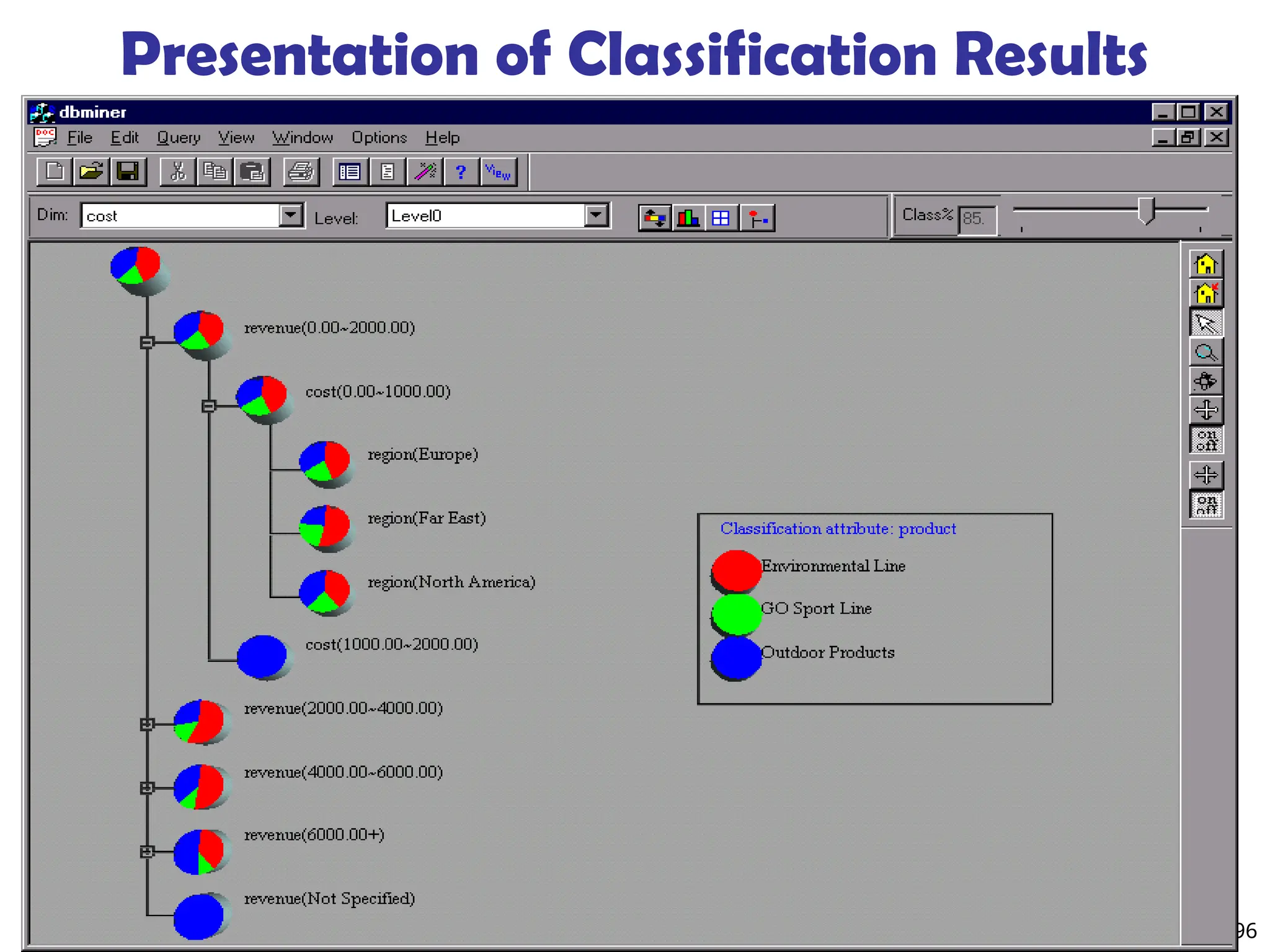
![219
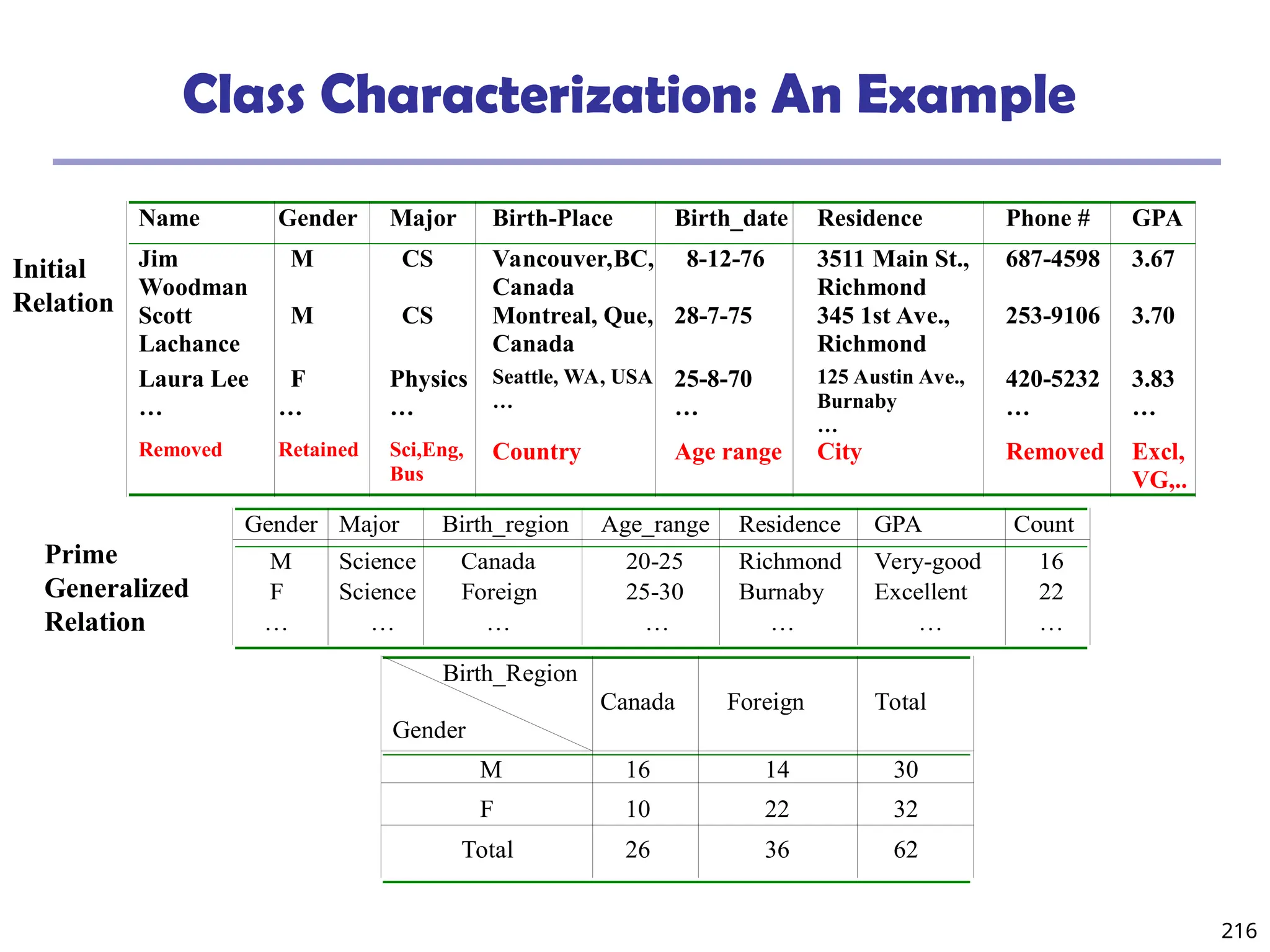
Presentation of Generalized Results
Generalized relation:
Relations where some or all attributes are generalized, with
counts or other aggregation values accumulated.
Cross tabulation:
Mapping results into cross tabulation form (similar to
contingency tables).
Visualization techniques:
Pie charts, bar charts, curves, cubes, and other visual forms.
Quantitative characteristic rules:
Mapping generalized result into characteristic rules with
quantitative information associated with it, e.g.,
.
%]
47
:
[
"
"
)
(
_
%]
53
:
[
"
"
)
(
_
)
(
)
(
t
foreign
x
region
birth
t
Canada
x
region
birth
x
male
x
grad
](https://image.slidesharecdn.com/dwdm3rdeditiontextbookslides-241024155956-ed696a42/75/DWDM-3rd-EDITION-TEXT-BOOK-SLIDES24-pptx-219-2048.jpg)

























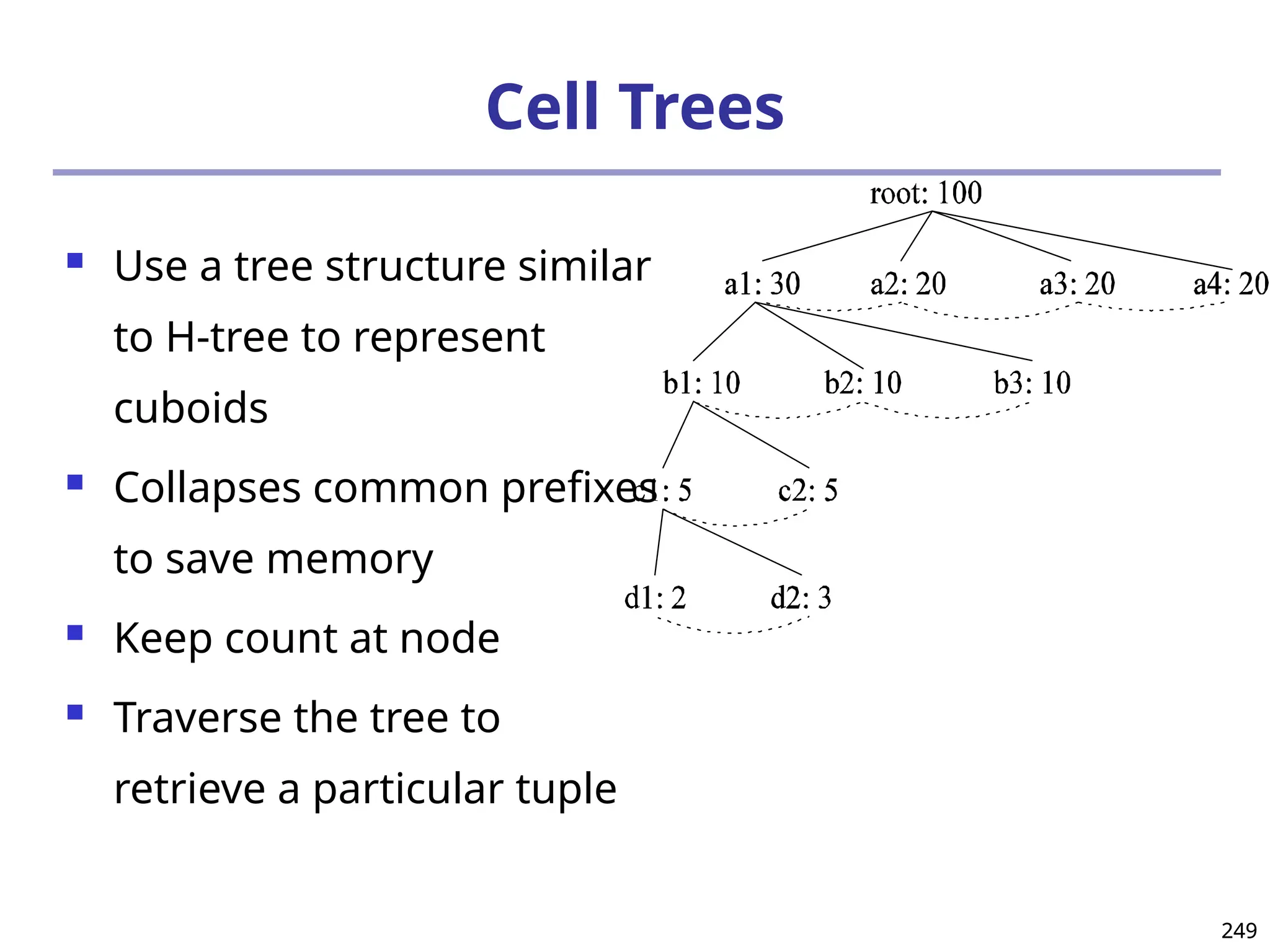



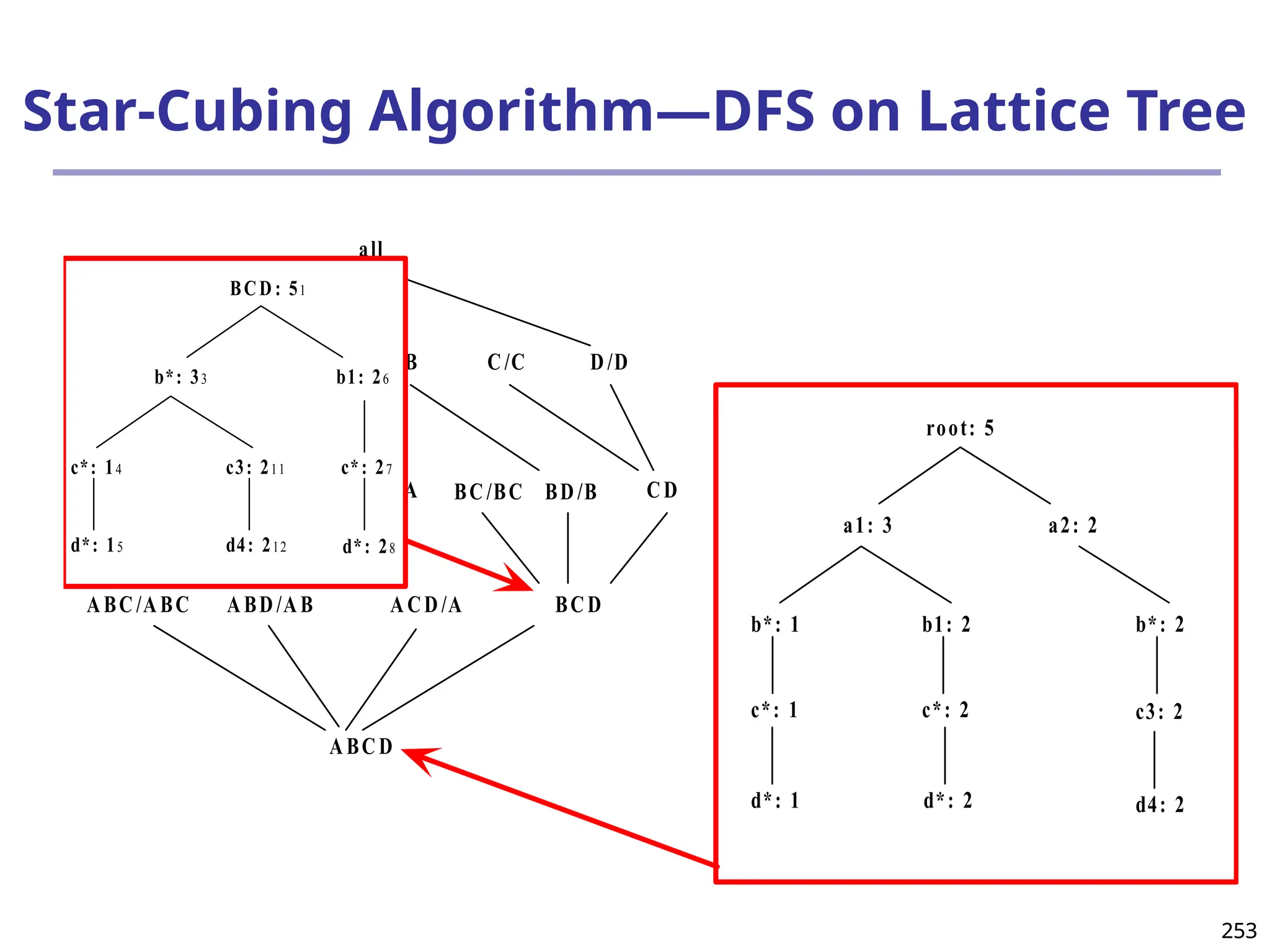




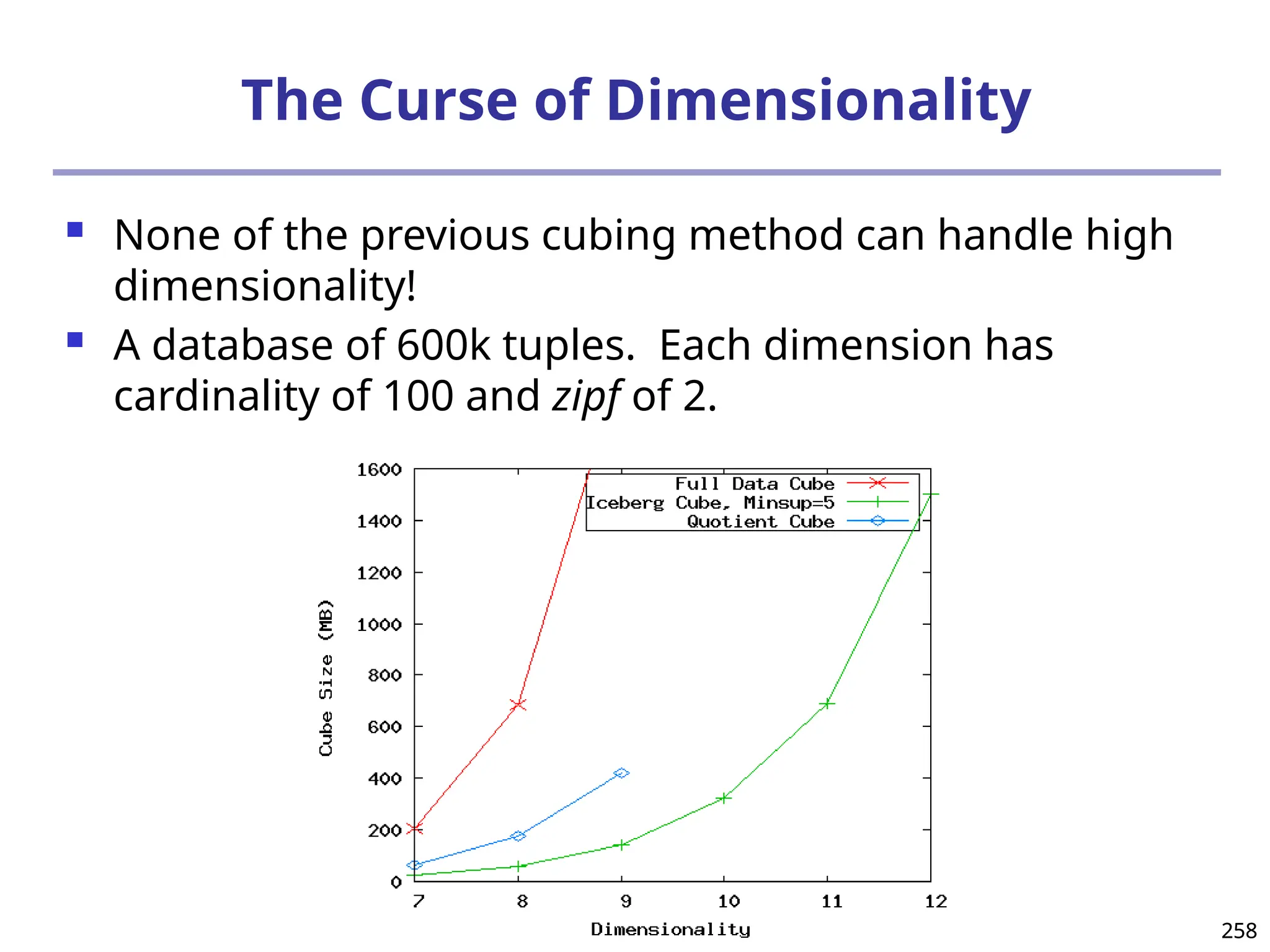



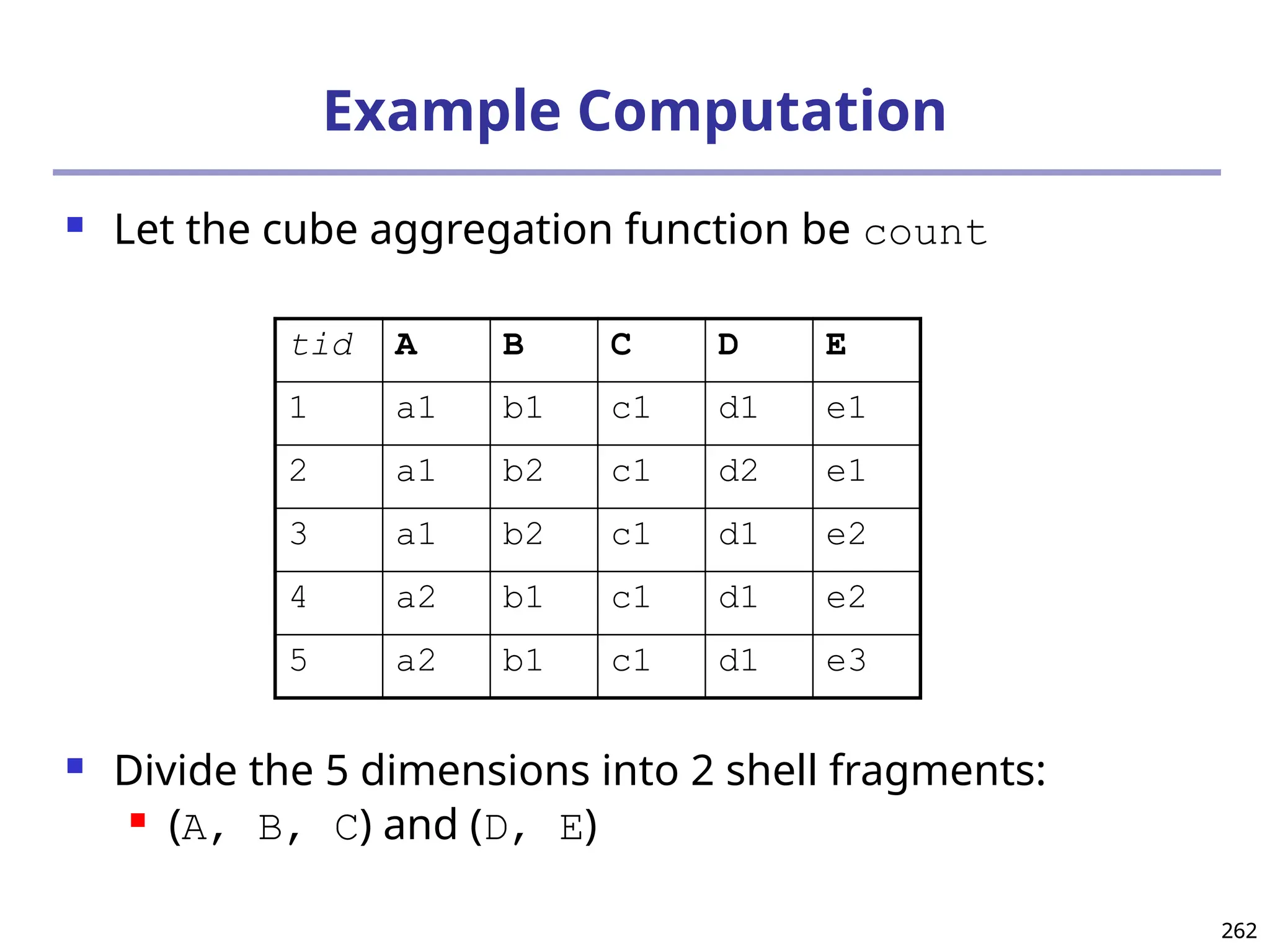



















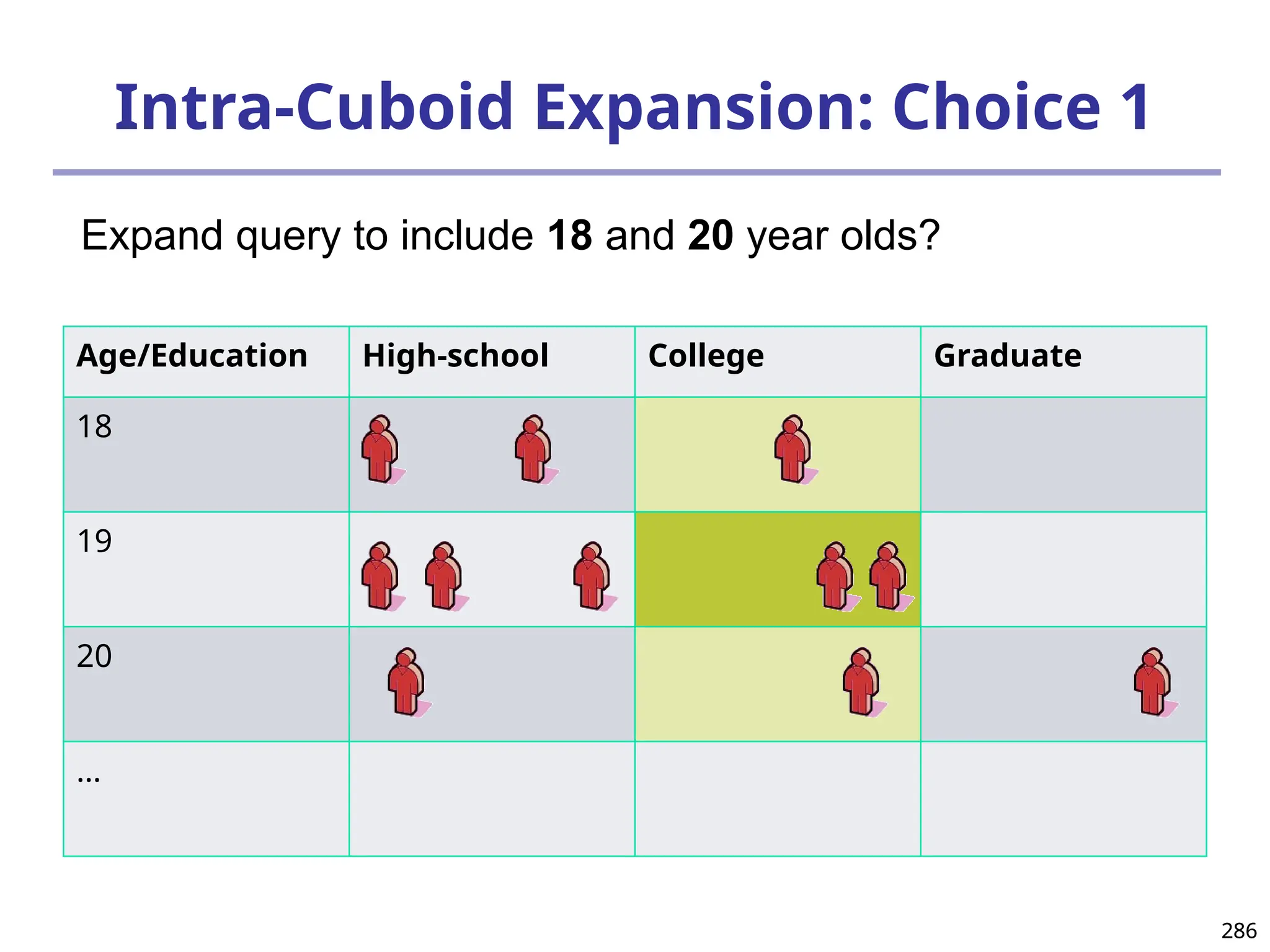
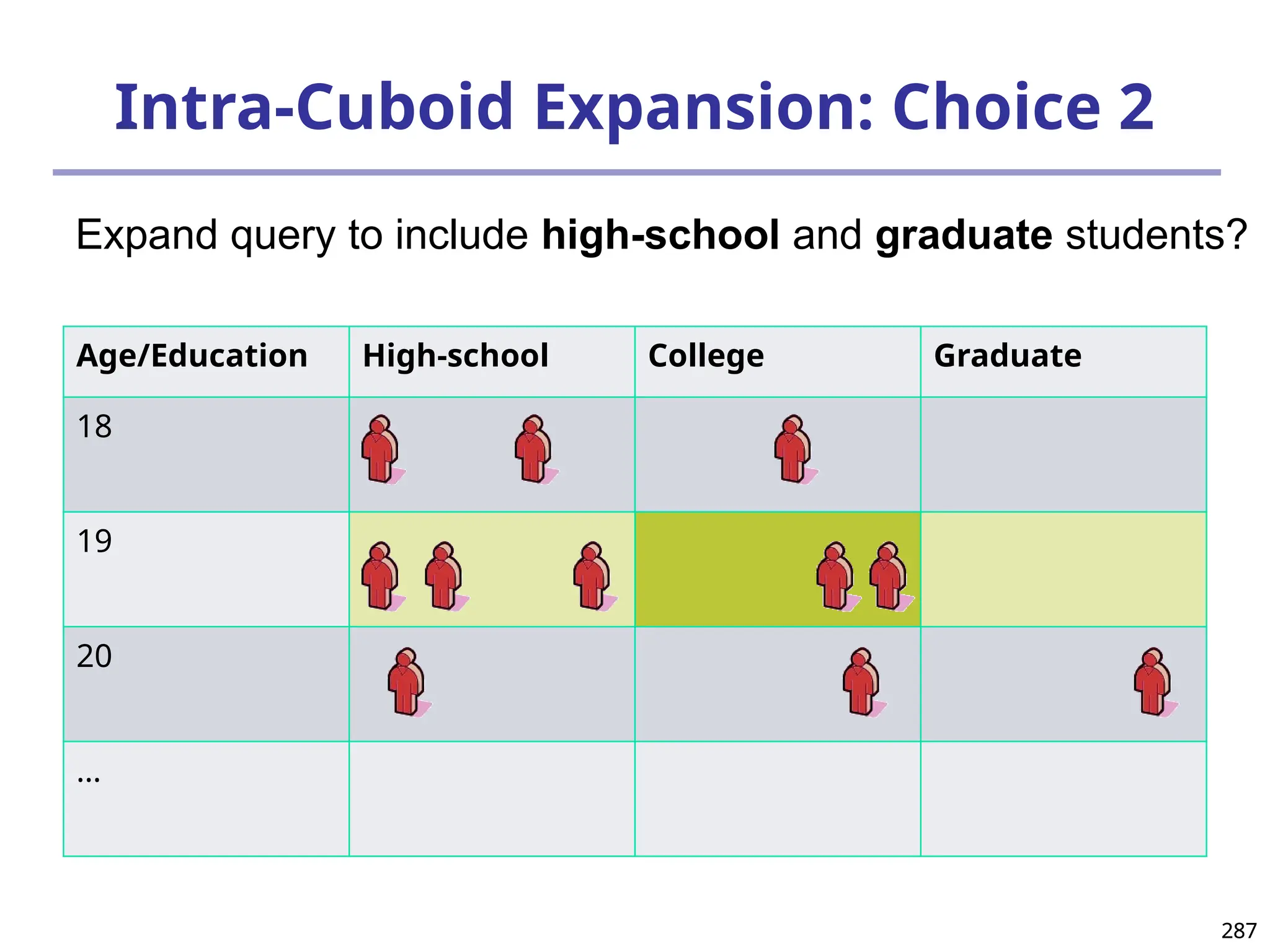





![293
Ranking Cubes – Efficient Computation of
Ranking queries
Data cube helps not only OLAP but also ranked search
(top-k) ranking query: only returns the best k results
according to a user-specified preference, consisting of
(1) a selection condition and (2) a ranking function
Ex.: Search for apartments with expected price 1000
and expected square feet 800
Select top 1 from Apartment
where City = “LA” and Num_Bedroom = 2
order by [price – 1000]^2 + [sq feet - 800]^2 asc
Efficiency question: Can we only search what we need?
Build a ranking cube on both selection dimensions
and ranking dimensions](https://image.slidesharecdn.com/dwdm3rdeditiontextbookslides-241024155956-ed696a42/75/DWDM-3rd-EDITION-TEXT-BOOK-SLIDES24-pptx-293-2048.jpg)

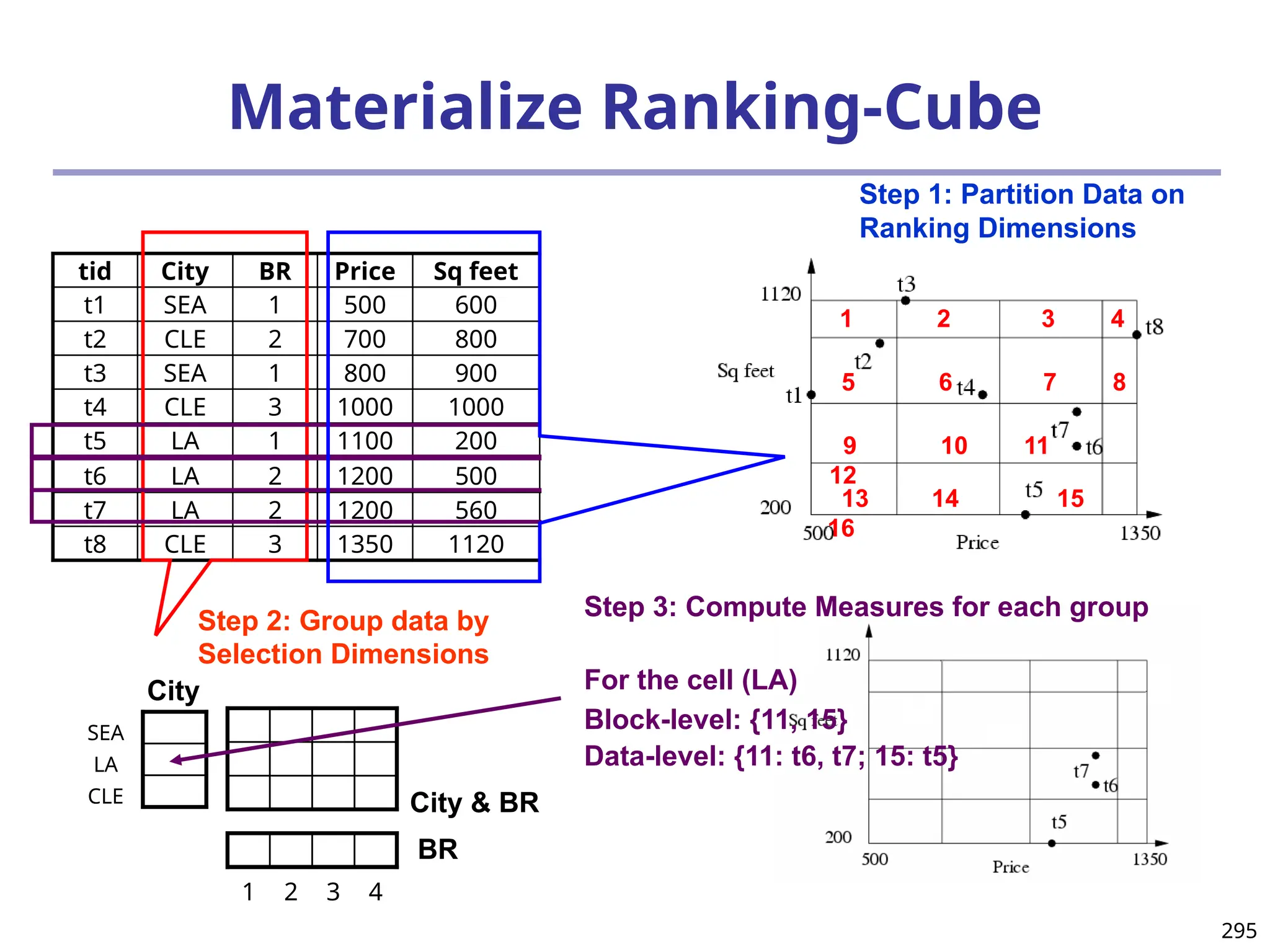
![296
Search with Ranking-Cube:
Simultaneously Push Selection and Ranking
Select top 1 from Apartment
where city = “LA”
order by [price – 1000]^2 + [sq feet - 800]^2 asc
800
1000
Without ranking-cube: start
search from here
With ranking-cube:
start search from here
Measure for
LA: {11, 15}
{11: t6,t7;
15:t5}
11
15
Given the bin boundaries,
locate the block with top score
Bin boundary for price [500, 600, 800, 1100,1350]
Bin boundary for sq feet [200, 400, 600, 800, 1120]](https://image.slidesharecdn.com/dwdm3rdeditiontextbookslides-241024155956-ed696a42/75/DWDM-3rd-EDITION-TEXT-BOOK-SLIDES24-pptx-296-2048.jpg)
![297
Processing Ranking Query: Execution Trace
Select top 1 from Apartment
where city = “LA”
order by [price – 1000]^2 + [sq feet - 800]^2 asc
800
1000
With ranking-
cube: start search
from here
Measure for
LA: {11, 15}
{11: t6,t7;
15:t5}
11
15
f=[price-1000]^2 + [sq feet – 800]^2
Bin boundary for price [500, 600, 800, 1100,1350]
Bin boundary for sq feet [200, 400, 600, 800, 1120]
Execution Trace:
1. Retrieve High-level measure for LA {11, 15}
2. Estimate lower bound score for block 11, 15
f(block 11) = 40,000, f(block 15) = 160,000
3. Retrieve block 11
4. Retrieve low-level measure for block 11
5. f(t6) = 130,000, f(t7) = 97,600
Output t7, done!](https://image.slidesharecdn.com/dwdm3rdeditiontextbookslides-241024155956-ed696a42/75/DWDM-3rd-EDITION-TEXT-BOOK-SLIDES24-pptx-297-2048.jpg)

















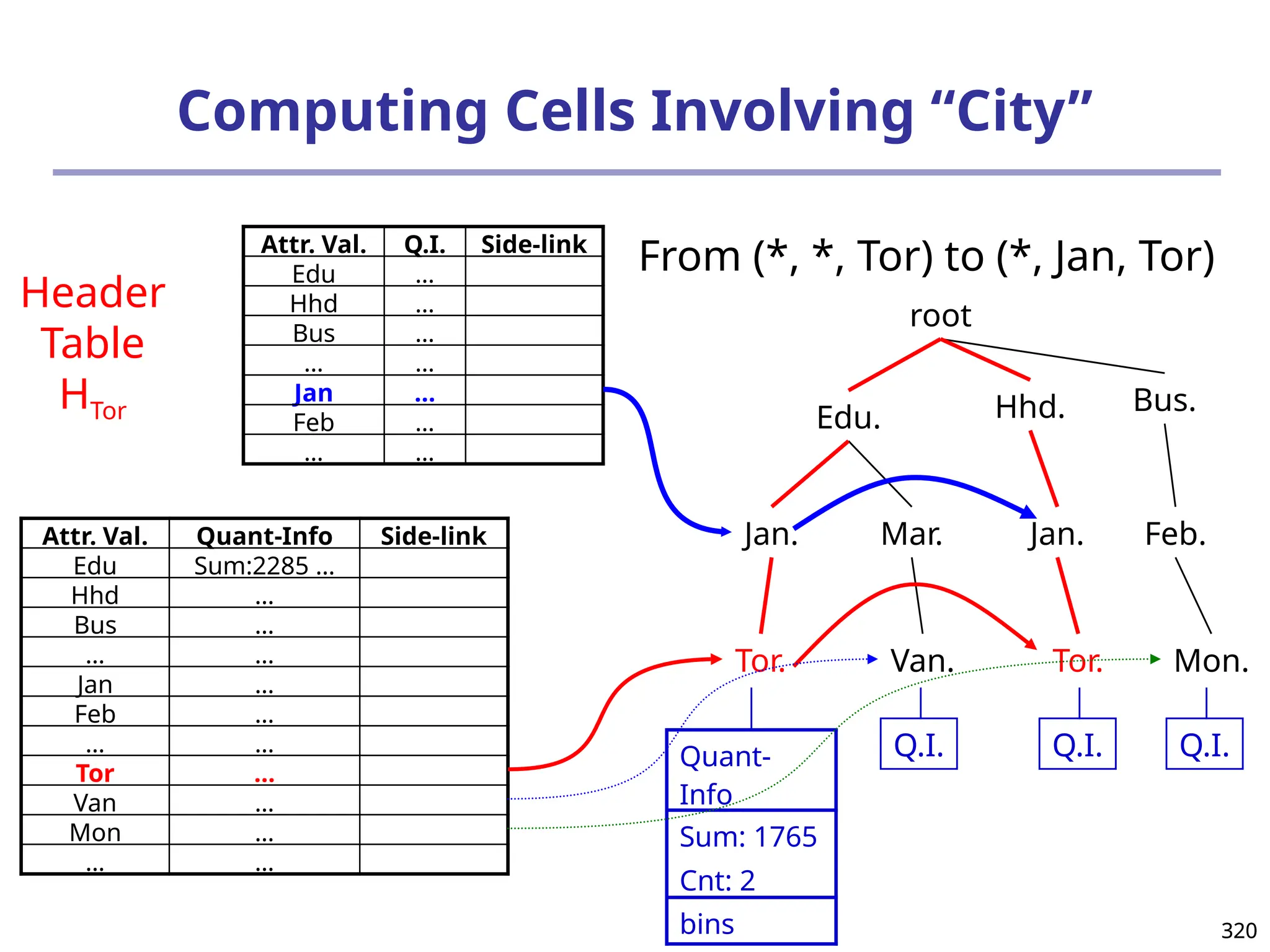
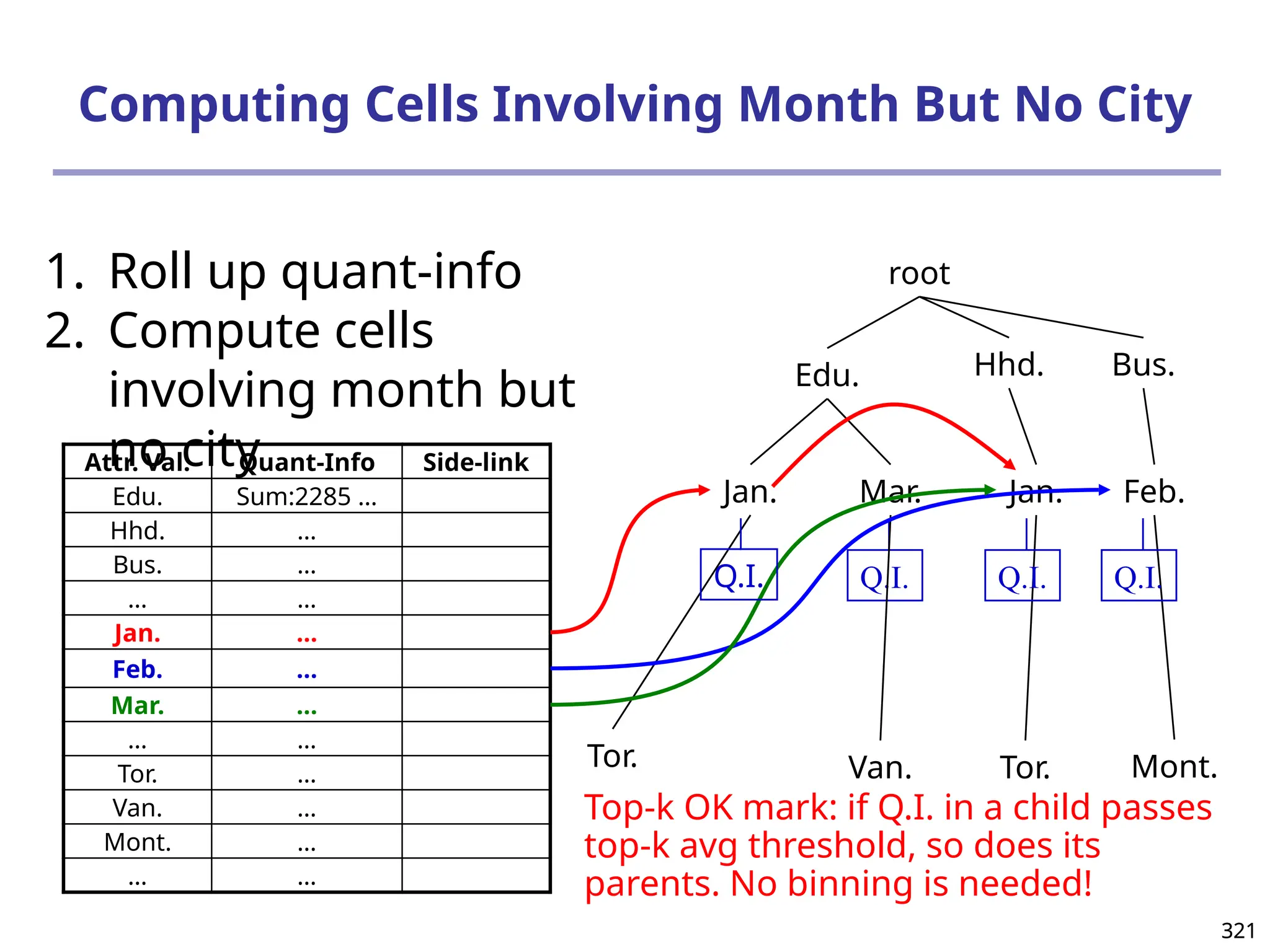



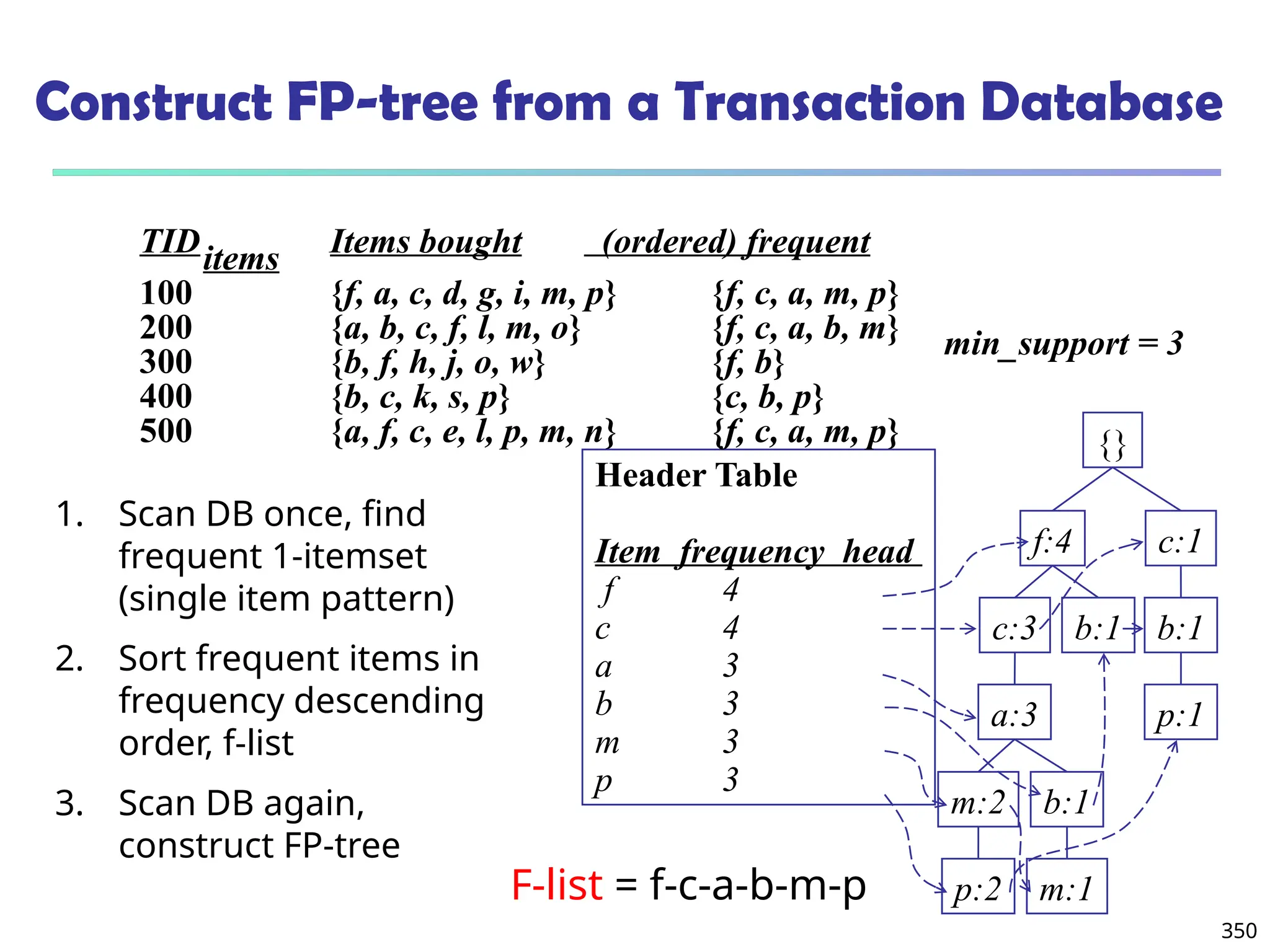
![325
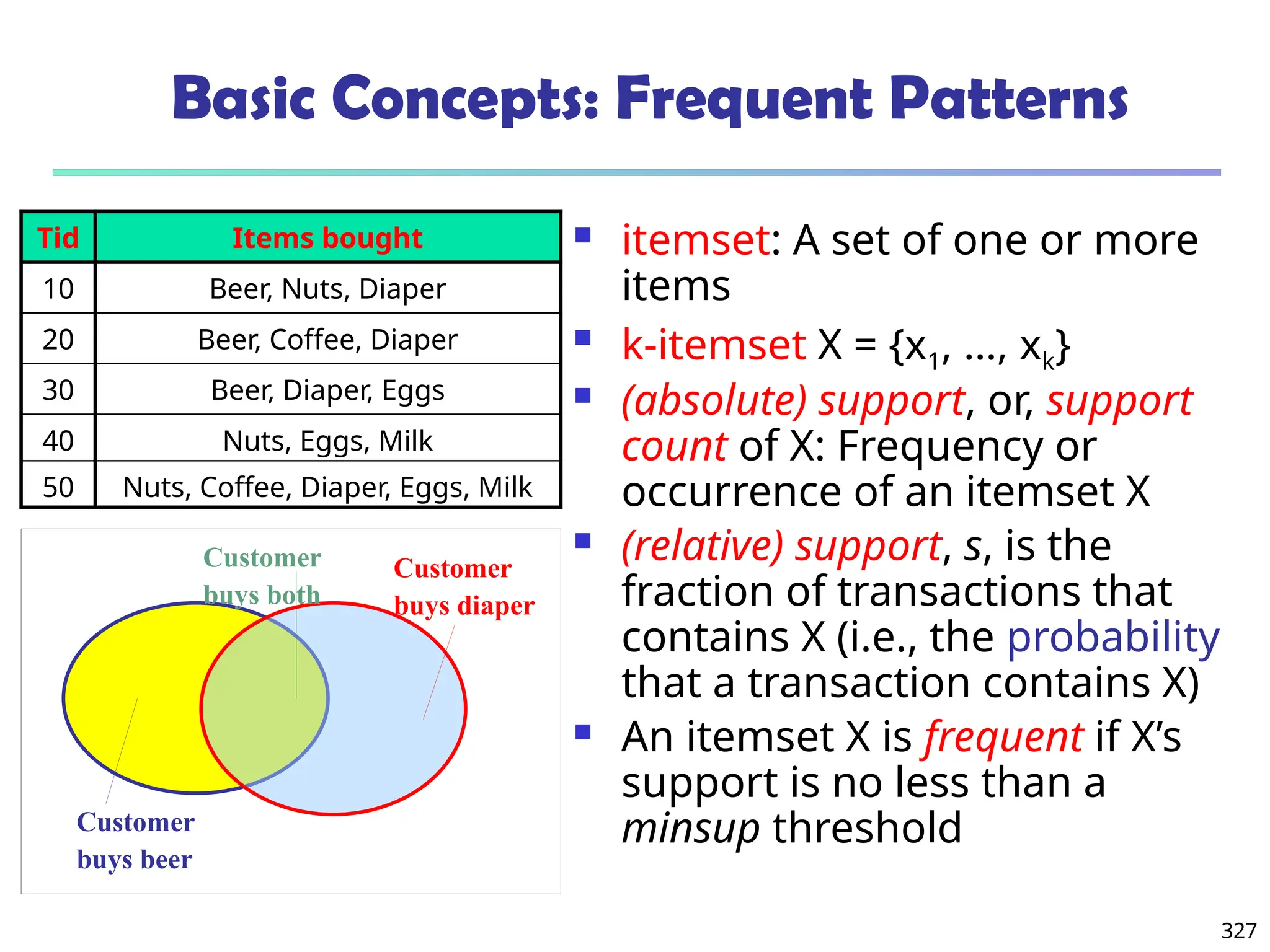
What Is Frequent Pattern Analysis?
Frequent pattern: a pattern (a set of items, subsequences,
substructures, etc.) that occurs frequently in a data set
First proposed by Agrawal, Imielinski, and Swami [AIS93] in the
context of frequent itemsets and association rule mining
Motivation: Finding inherent regularities in data
What products were often purchased together?— Beer and
diapers?!
What are the subsequent purchases after buying a PC?
What kinds of DNA are sensitive to this new drug?
Can we automatically classify web documents?
Applications
Basket data analysis, cross-marketing, catalog design, sale
campaign analysis, Web log (click stream) analysis, and DNA](https://image.slidesharecdn.com/dwdm3rdeditiontextbookslides-241024155956-ed696a42/75/DWDM-3rd-EDITION-TEXT-BOOK-SLIDES24-pptx-325-2048.jpg)














![341
Candidate Generation: An SQL Implementation
SQL Implementation of candidate generation
Suppose the items in Lk-1 are listed in an order
Step 1: self-joining Lk-1
insert into Ck
select p.item1, p.item2, …, p.itemk-1, q.itemk-1
from Lk-1 p, Lk-1 q
where p.item1=q.item1, …, p.itemk-2=q.itemk-2, p.itemk-1 < q.itemk-1
Step 2: pruning
forall itemsets c in Ck do
forall (k-1)-subsets s of c do
if (s is not in Lk-1) then delete c from Ck
Use object-relational extensions like UDFs, BLOBs, and Table functions for
efficient implementation [See: S. Sarawagi, S. Thomas, and R. Agrawal.
Integrating association rule mining with relational database systems:
Alternatives and implications. SIGMOD’98]](https://image.slidesharecdn.com/dwdm3rdeditiontextbookslides-241024155956-ed696a42/75/DWDM-3rd-EDITION-TEXT-BOOK-SLIDES24-pptx-341-2048.jpg)








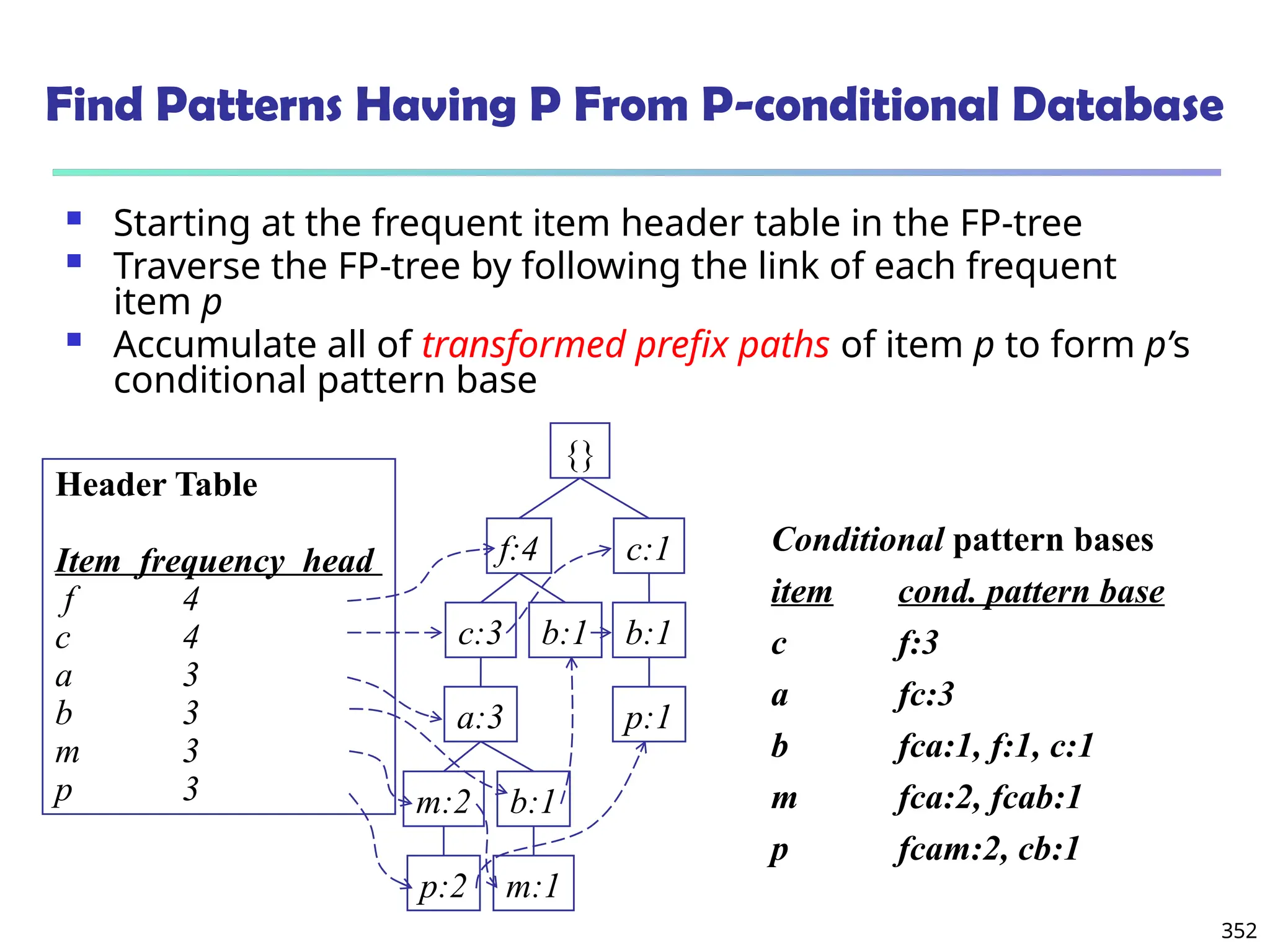






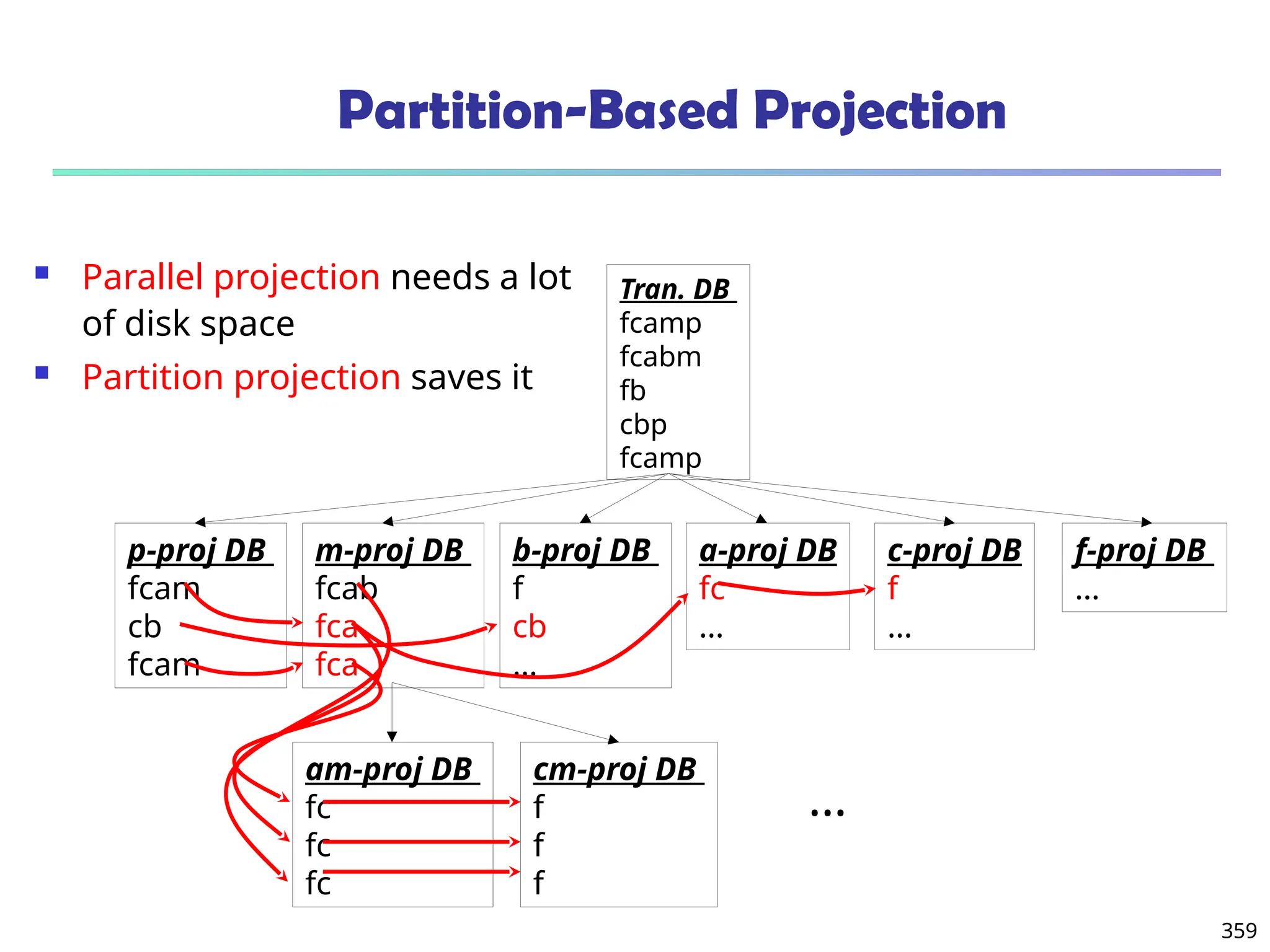
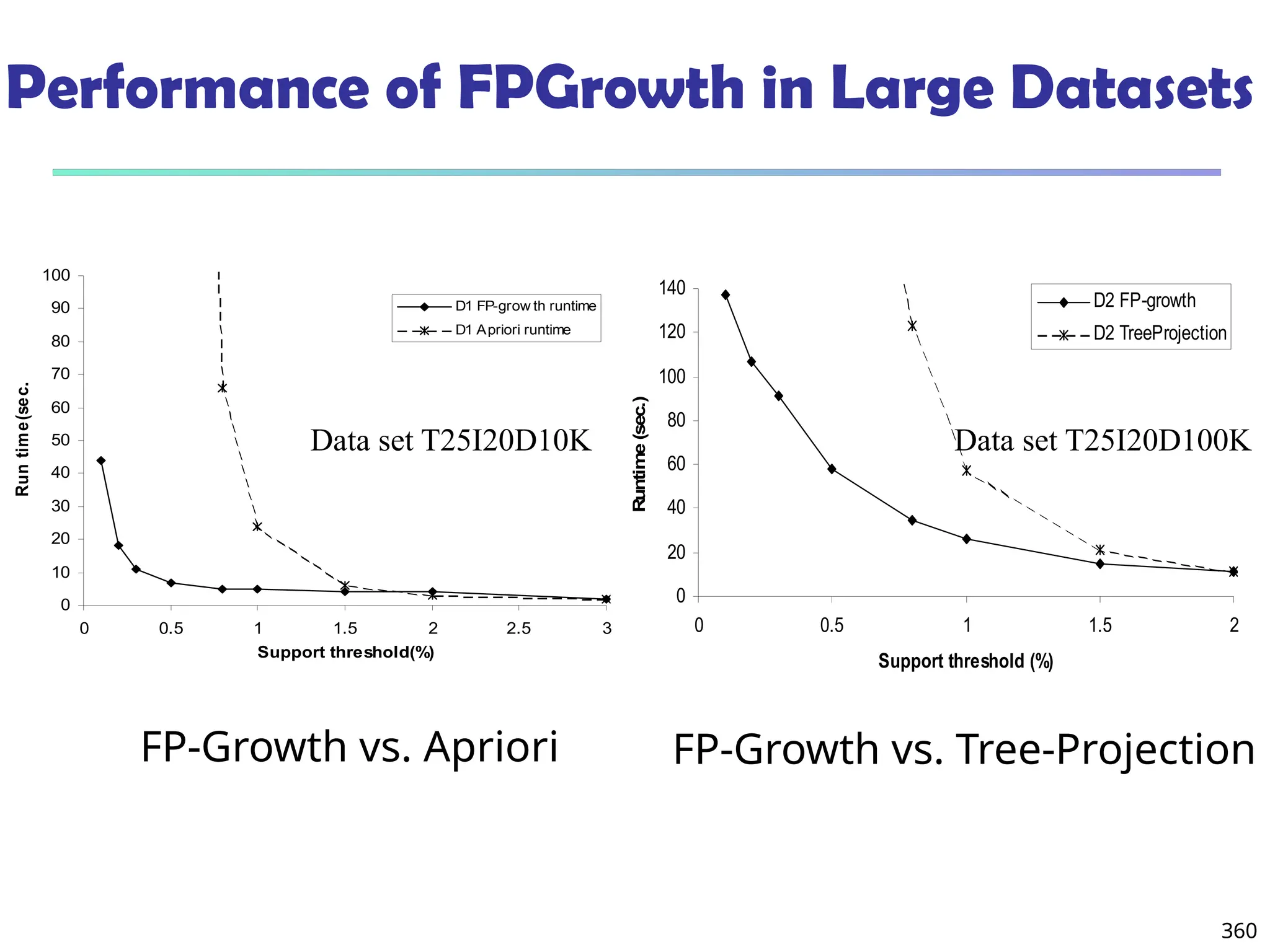










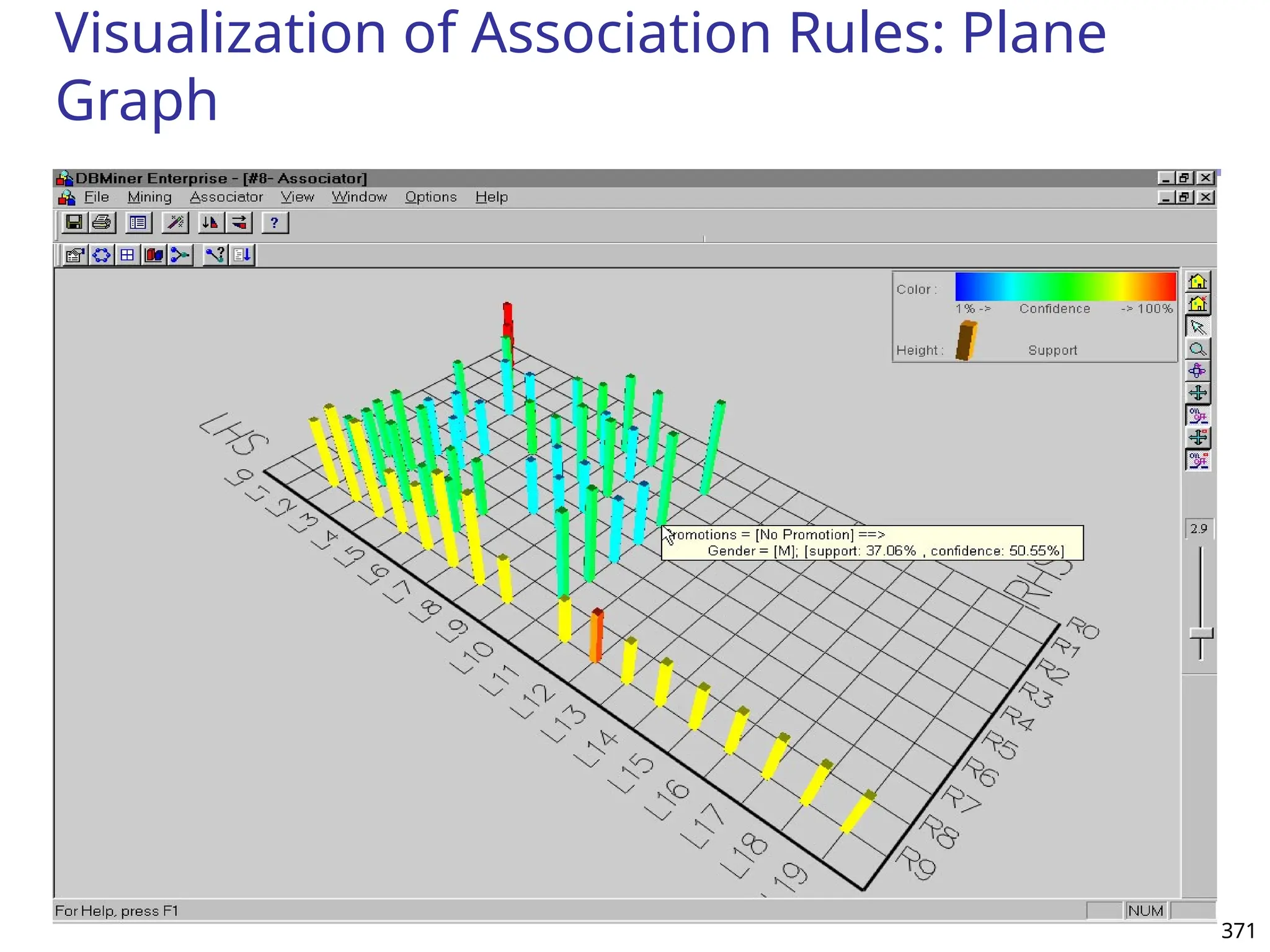
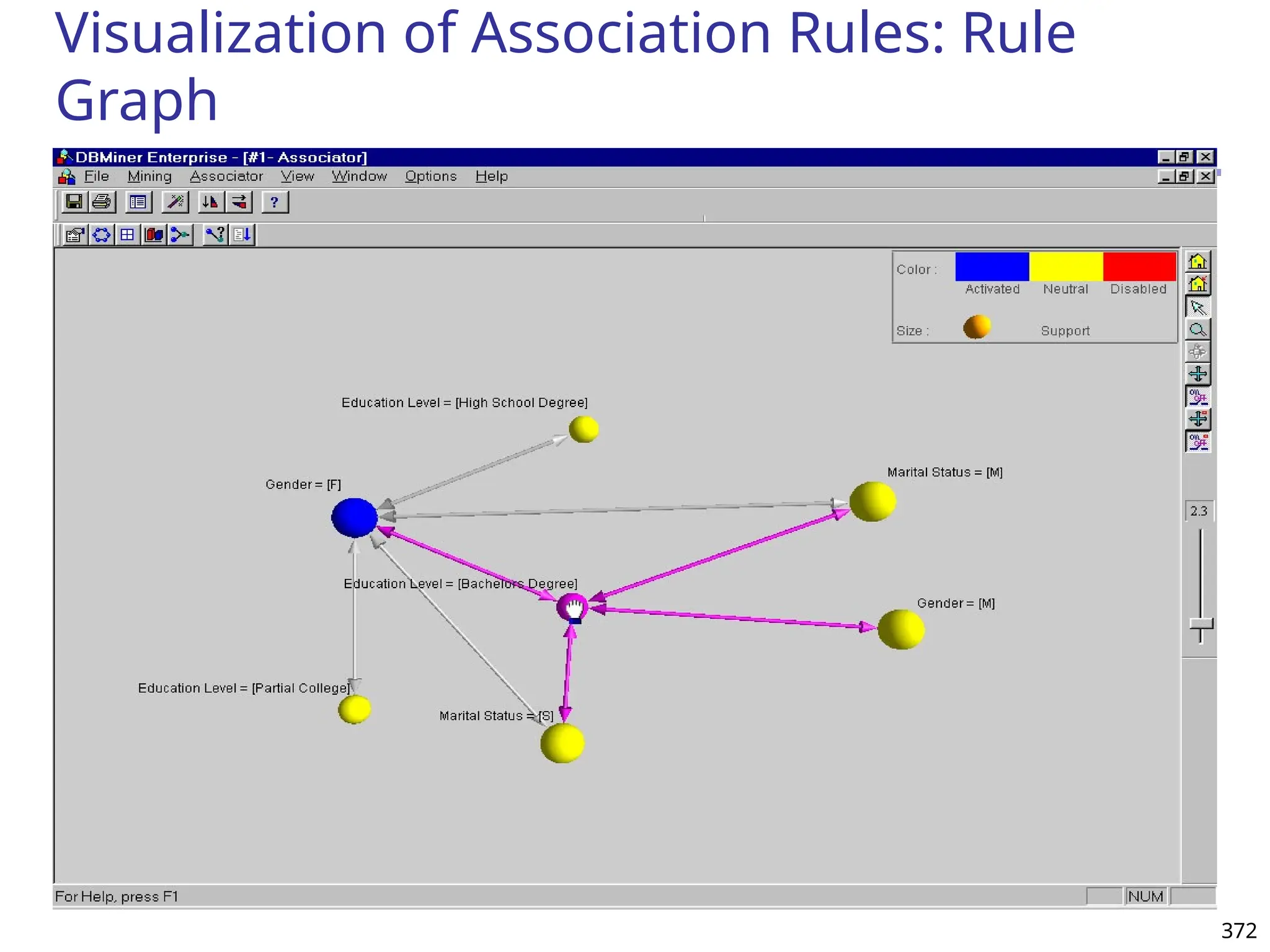

![375
Interestingness Measure: Correlations (Lift)
play basketball eat cereal [40%, 66.7%] is misleading
The overall % of students eating cereal is 75% > 66.7%.
play basketball not eat cereal [20%, 33.3%] is more accurate,
although with lower support and confidence
Measure of dependent/correlated events: lift
89
.
0
5000
/
3750
*
5000
/
3000
5000
/
2000
)
,
(
C
B
lift
Basketbal
l
Not
basketball
Sum (row)
Cereal 2000 1750 3750
Not cereal 1000 250 1250
Sum(col.) 3000 2000 5000
)
(
)
(
)
(
B
P
A
P
B
A
P
lift
33
.
1
5000
/
1250
*
5000
/
3000
5000
/
1000
)
,
(
C
B
lift](https://image.slidesharecdn.com/dwdm3rdeditiontextbookslides-241024155956-ed696a42/75/DWDM-3rd-EDITION-TEXT-BOOK-SLIDES24-pptx-375-2048.jpg)
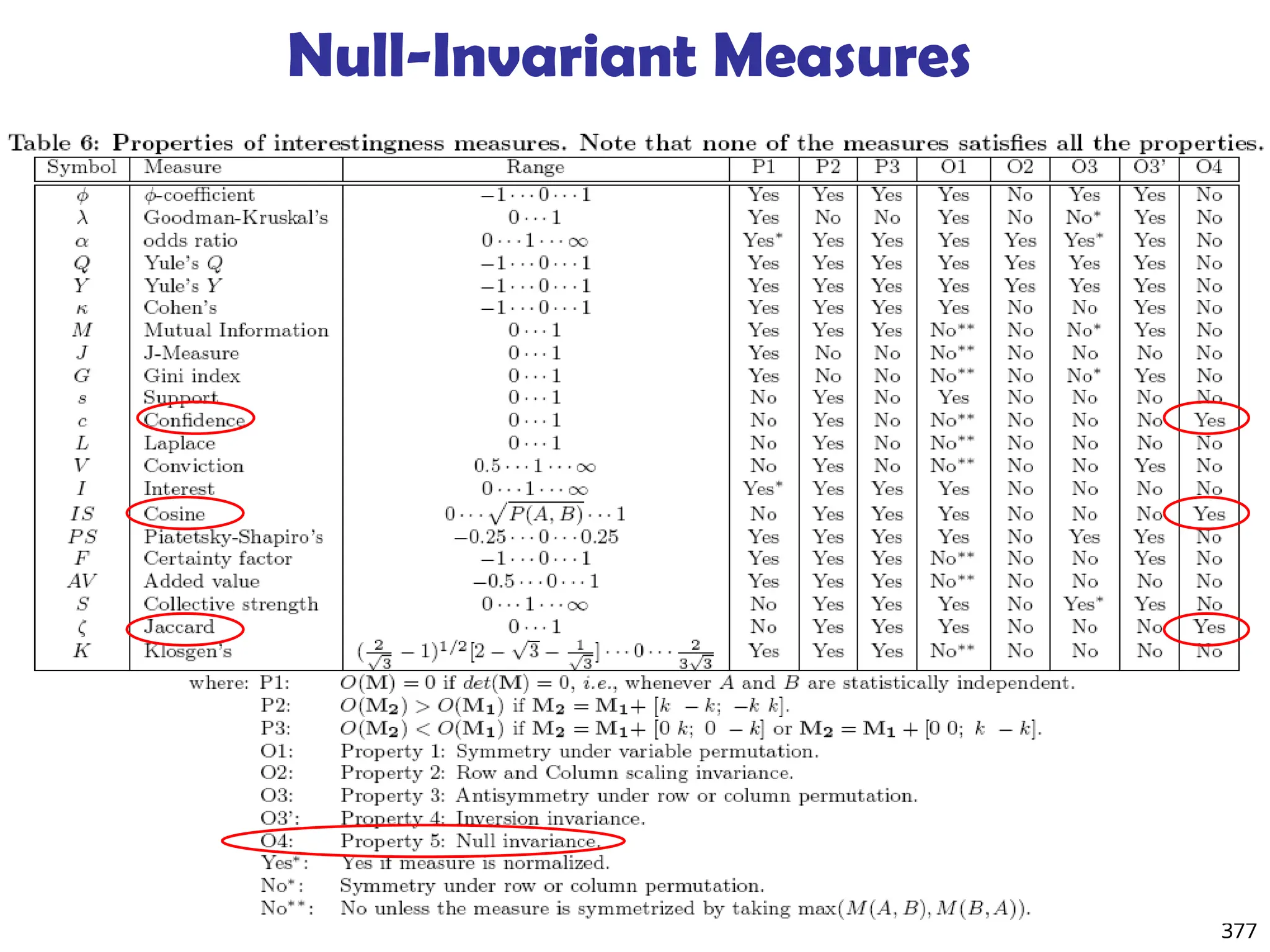
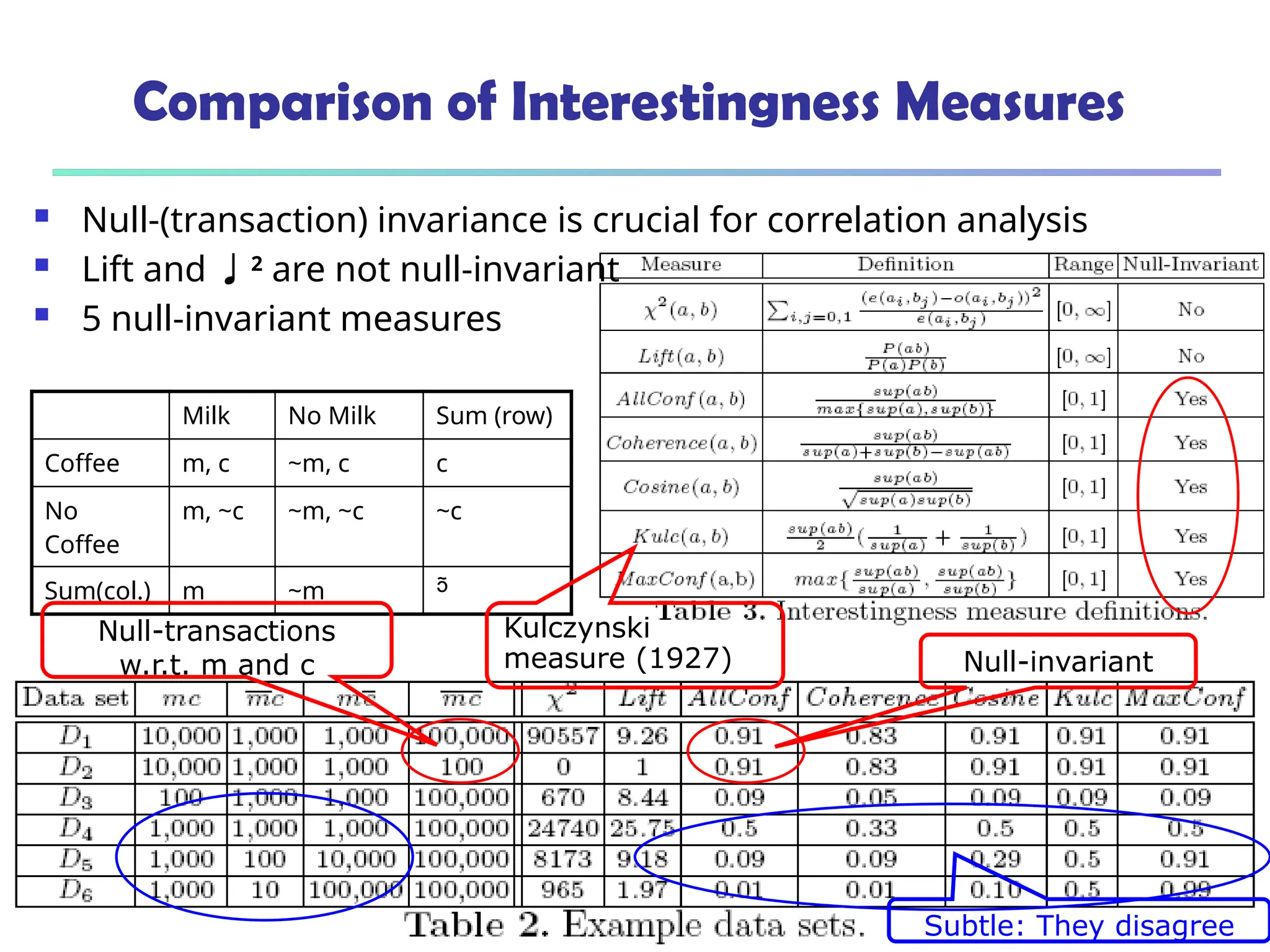
![376
Are lift and 2
Good Measures of Correlation?
“Buy walnuts buy
milk [1%, 80%]” is
misleading if 85% of
customers buy milk
Support and
confidence are not
good to indicate
correlations
Over 20
interestingness
measures have been
proposed (see Tan,
Kumar, Sritastava
@KDD’02)
Which are good ones?](https://image.slidesharecdn.com/dwdm3rdeditiontextbookslides-241024155956-ed696a42/75/DWDM-3rd-EDITION-TEXT-BOOK-SLIDES24-pptx-376-2048.jpg)













![393
Mining Multiple-Level Association Rules
Items often form hierarchies
Flexible support settings
Items at the lower level are expected to have lower
support
Exploration of shared multi-level mining (Agrawal &
Srikant@VLB’95, Han & Fu@VLDB’95)
uniform
support
Milk
[support = 10%]
2% Milk
[support = 6%]
Skim Milk
[support = 4%]
Level 1
min_sup = 5%
Level 2
min_sup = 5%
Level 1
min_sup = 5%
Level 2
min_sup = 3%
reduced support](https://image.slidesharecdn.com/dwdm3rdeditiontextbookslides-241024155956-ed696a42/75/DWDM-3rd-EDITION-TEXT-BOOK-SLIDES24-pptx-393-2048.jpg)
![394
Multi-level Association: Flexible Support and
Redundancy filtering
Flexible min-support thresholds: Some items are more valuable
but less frequent
Use non-uniform, group-based min-support
E.g., {diamond, watch, camera}: 0.05%; {bread, milk}: 5%; …
Redundancy Filtering: Some rules may be redundant due to
“ancestor” relationships between items
milk wheat bread [support = 8%, confidence = 70%]
2% milk wheat bread [support = 2%, confidence = 72%]
The first rule is an ancestor of the second rule
A rule is redundant if its support is close to the “expected” value,
based on the rule’s ancestor](https://image.slidesharecdn.com/dwdm3rdeditiontextbookslides-241024155956-ed696a42/75/DWDM-3rd-EDITION-TEXT-BOOK-SLIDES24-pptx-394-2048.jpg)





![400
Quantitative Association Rules Based on Statistical
Inference Theory [Aumann and Lindell@DMKD’03]
Finding extraordinary and therefore interesting phenomena, e.g.,
(Sex = female) => Wage: mean=$7/hr (overall mean = $9)
LHS: a subset of the population
RHS: an extraordinary behavior of this subset
The rule is accepted only if a statistical test (e.g., Z-test) confirms
the inference with high confidence
Subrule: highlights the extraordinary behavior of a subset of the
pop. of the super rule
E.g., (Sex = female) ^ (South = yes) => mean wage = $6.3/hr
Two forms of rules
Categorical => quantitative rules, or Quantitative => quantitative rules
E.g., Education in [14-18] (yrs) => mean wage = $11.64/hr
Open problem: Efficient methods for LHS containing two or more
quantitative attributes](https://image.slidesharecdn.com/dwdm3rdeditiontextbookslides-241024155956-ed696a42/75/DWDM-3rd-EDITION-TEXT-BOOK-SLIDES24-pptx-400-2048.jpg)









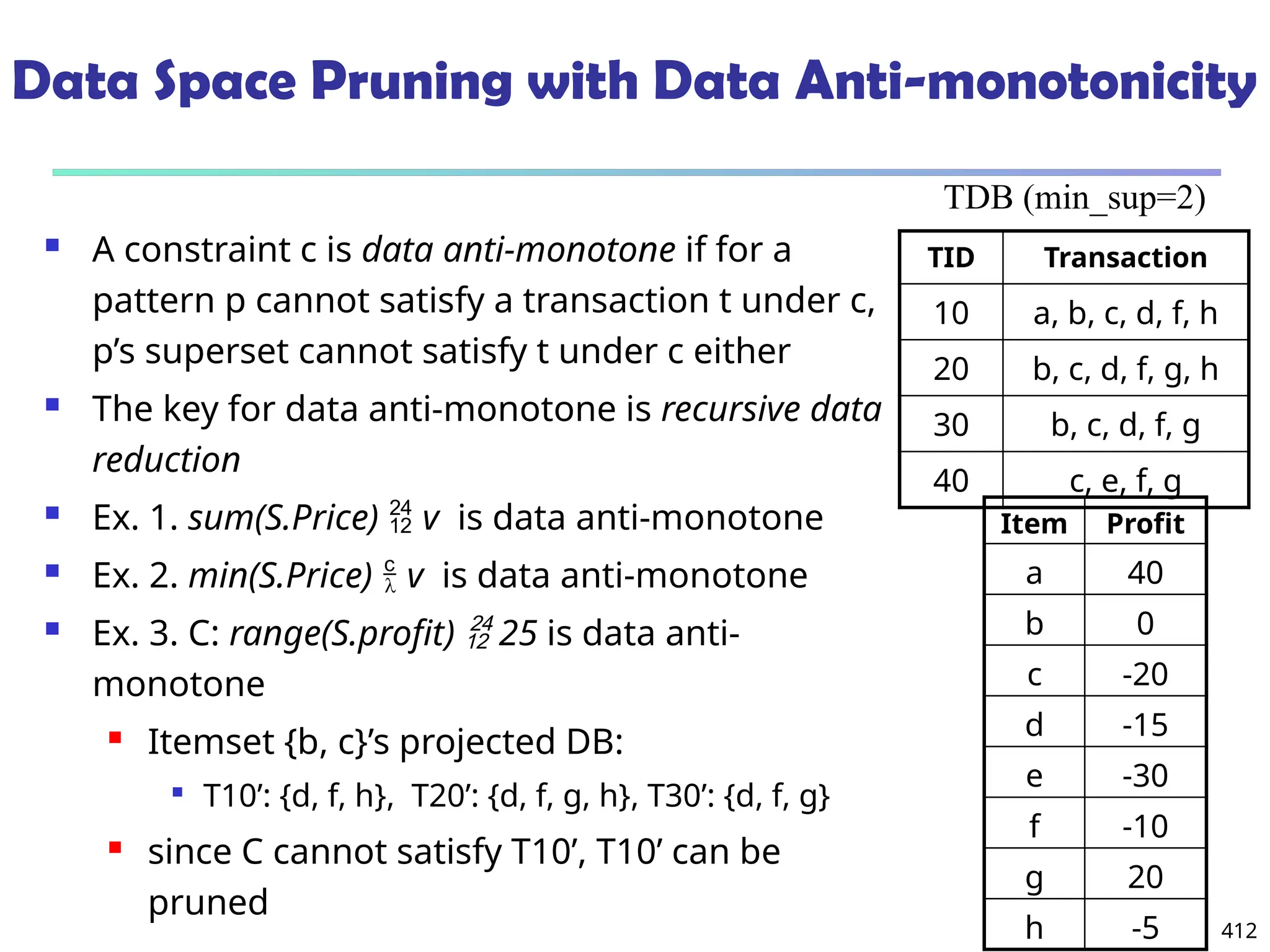

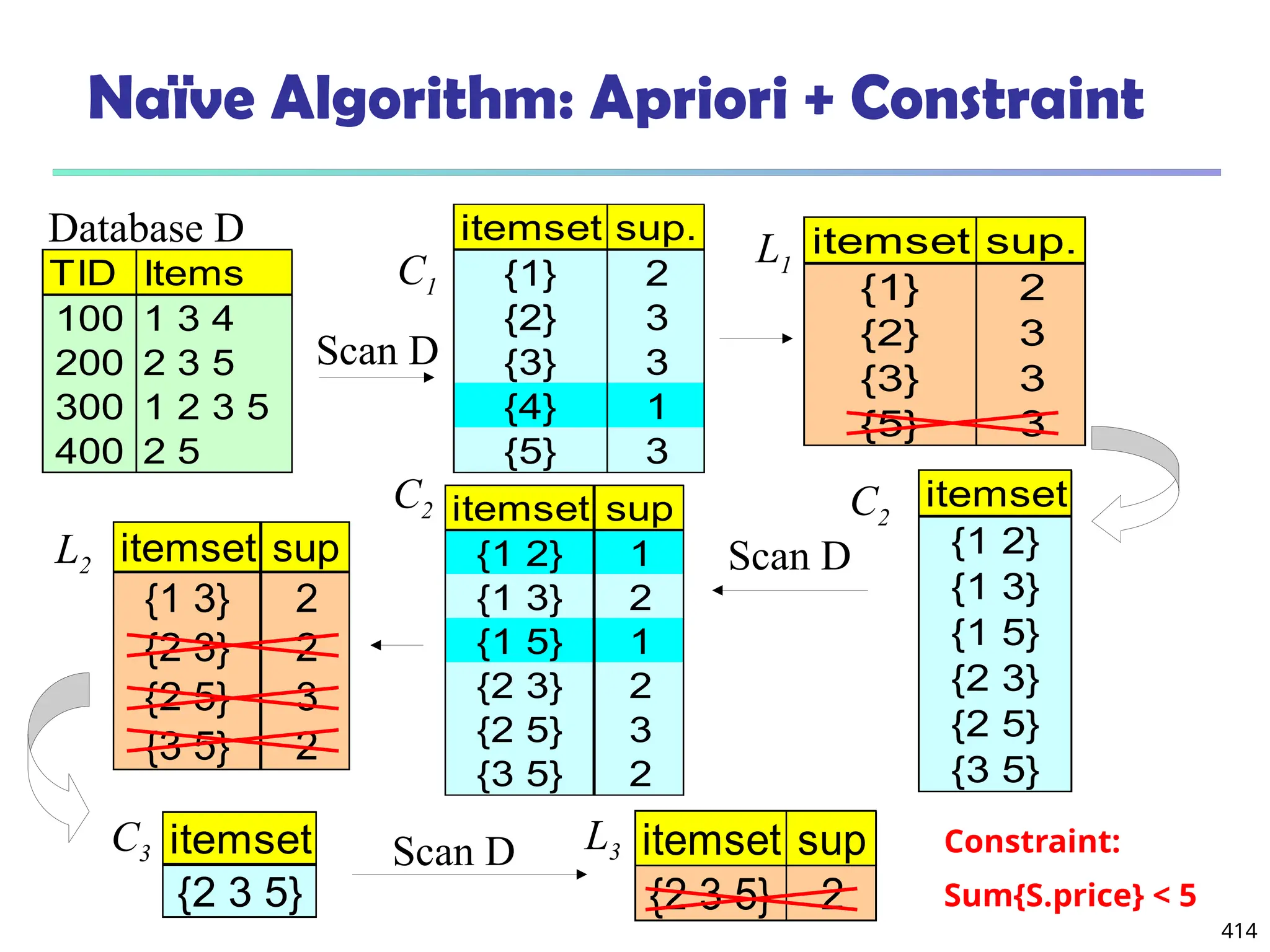
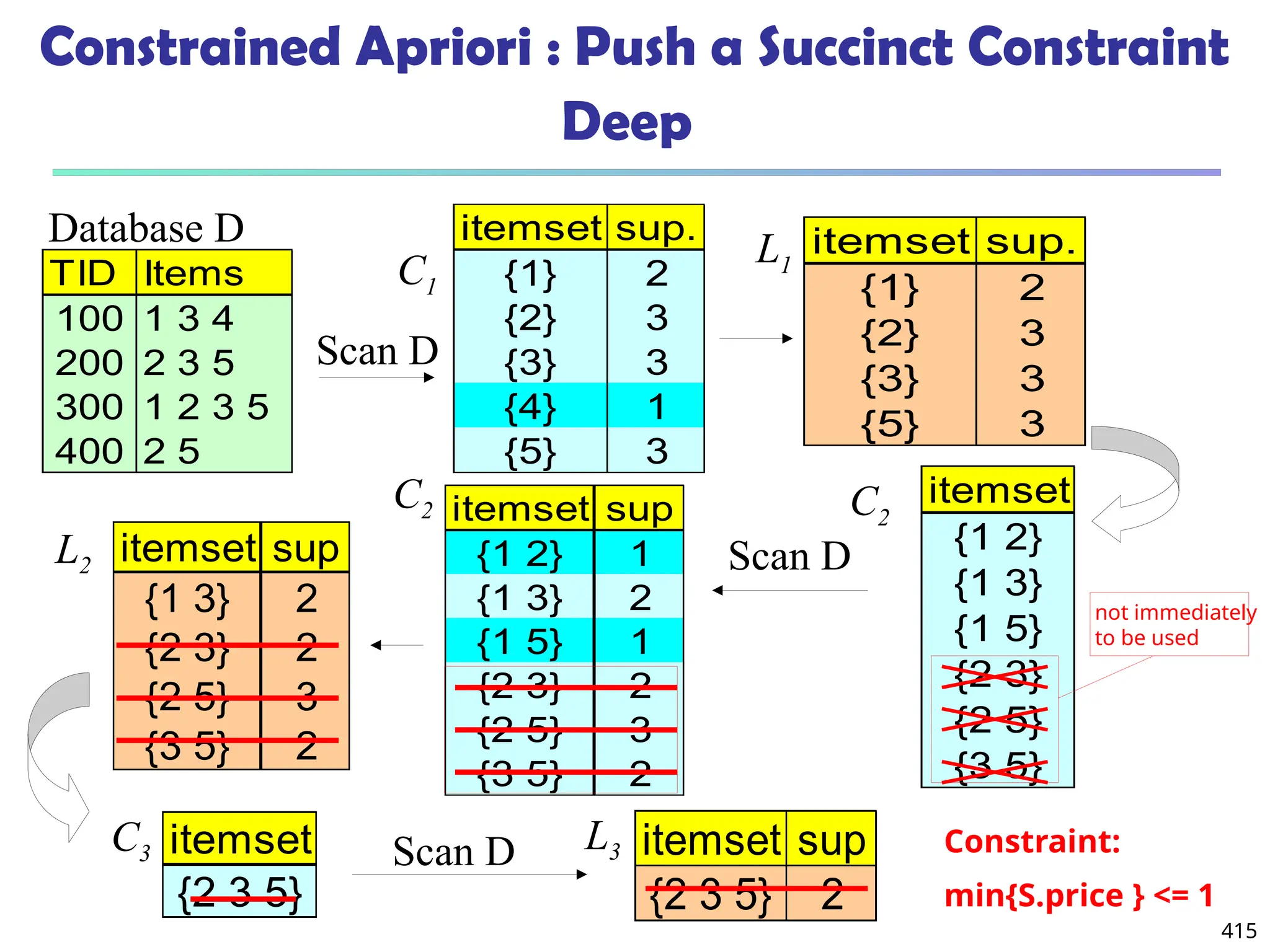

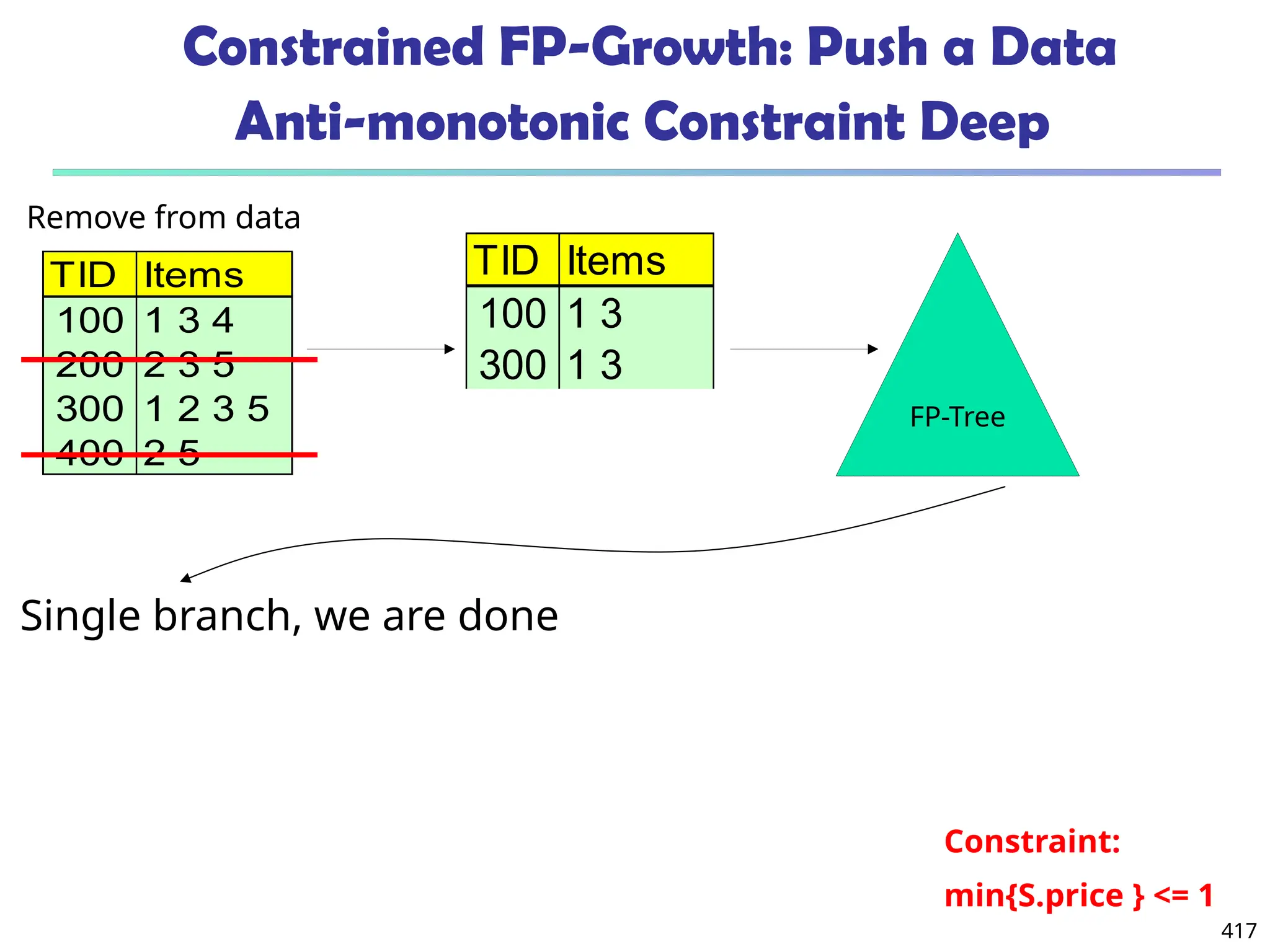
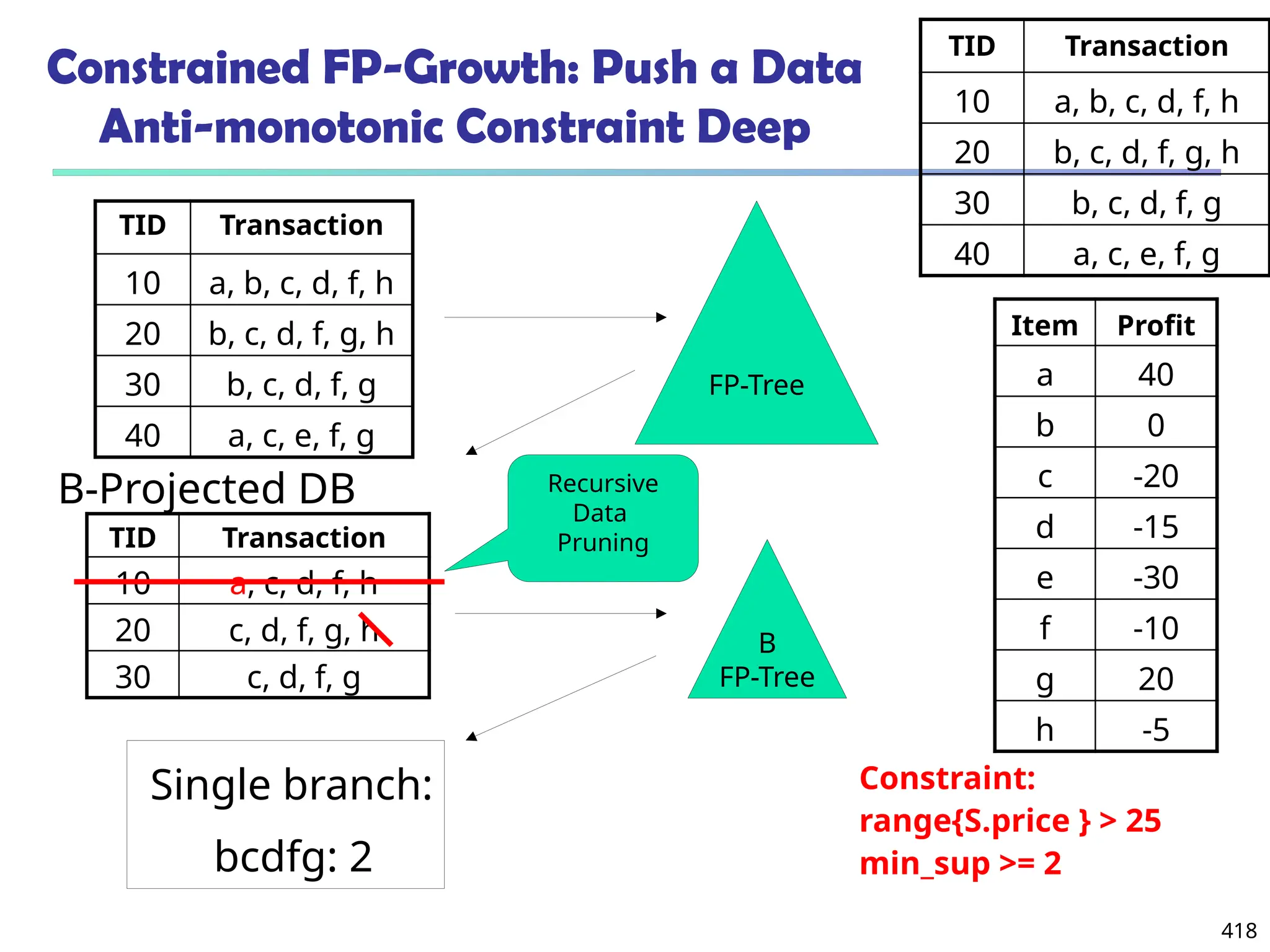
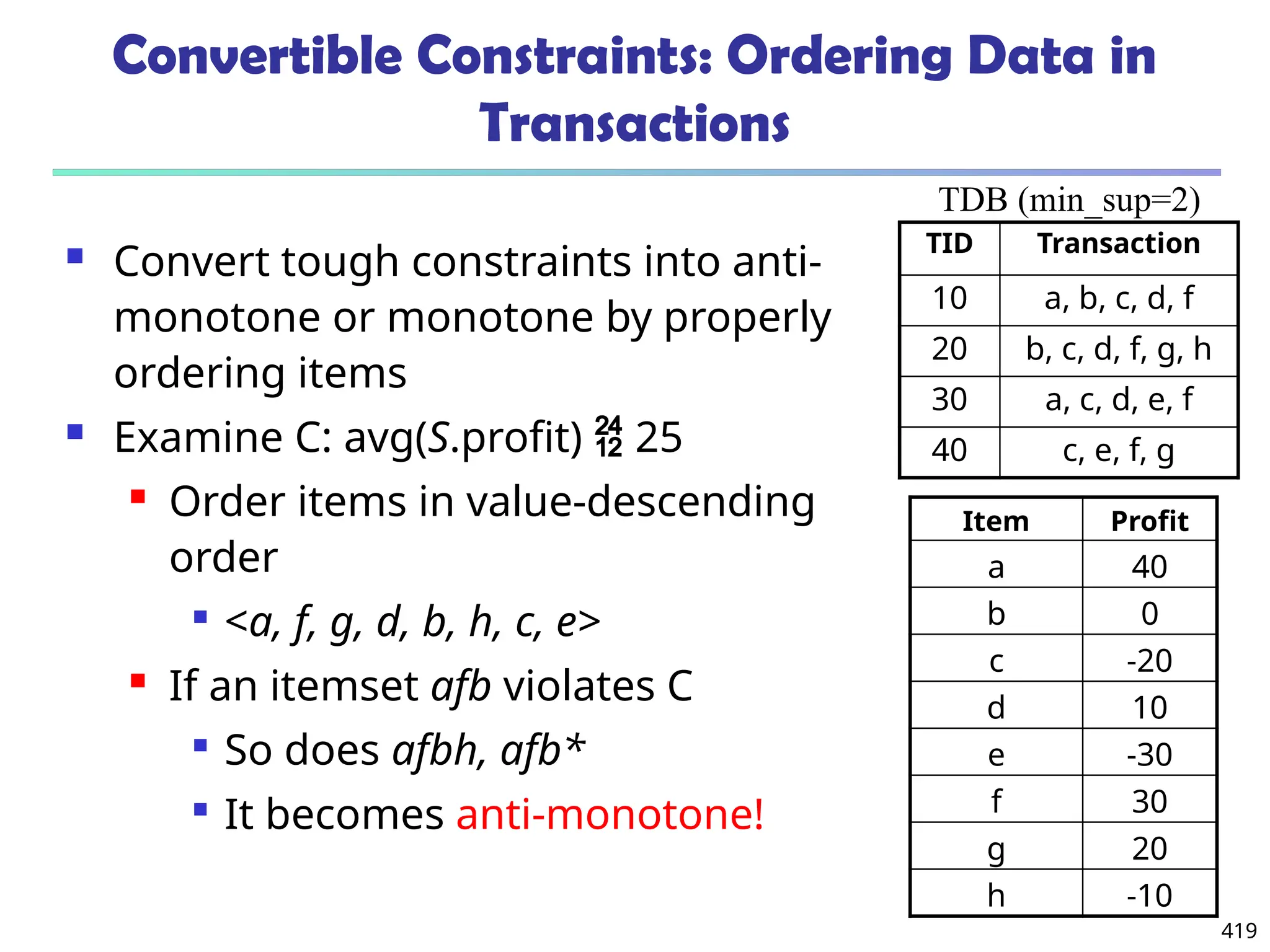

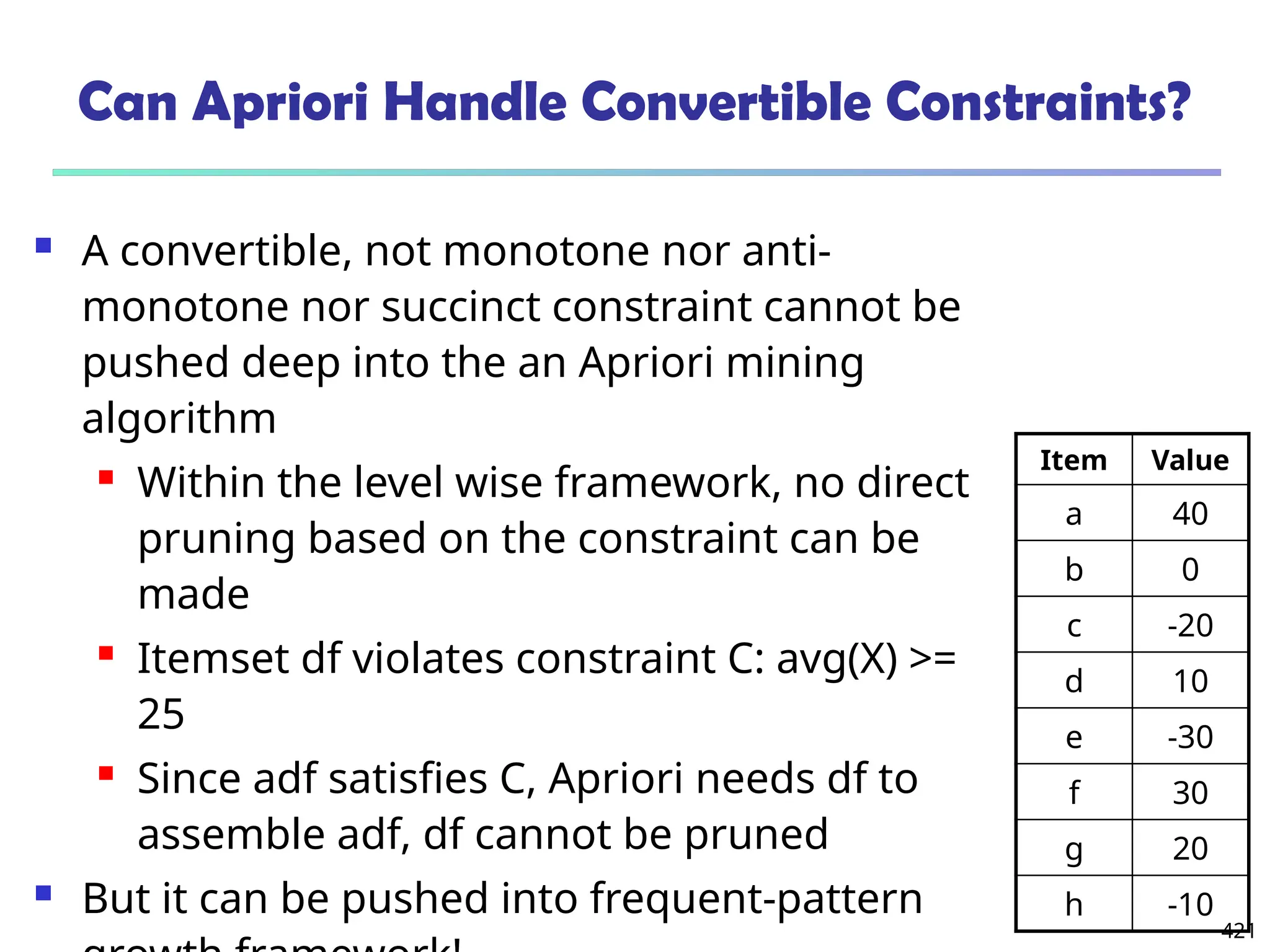
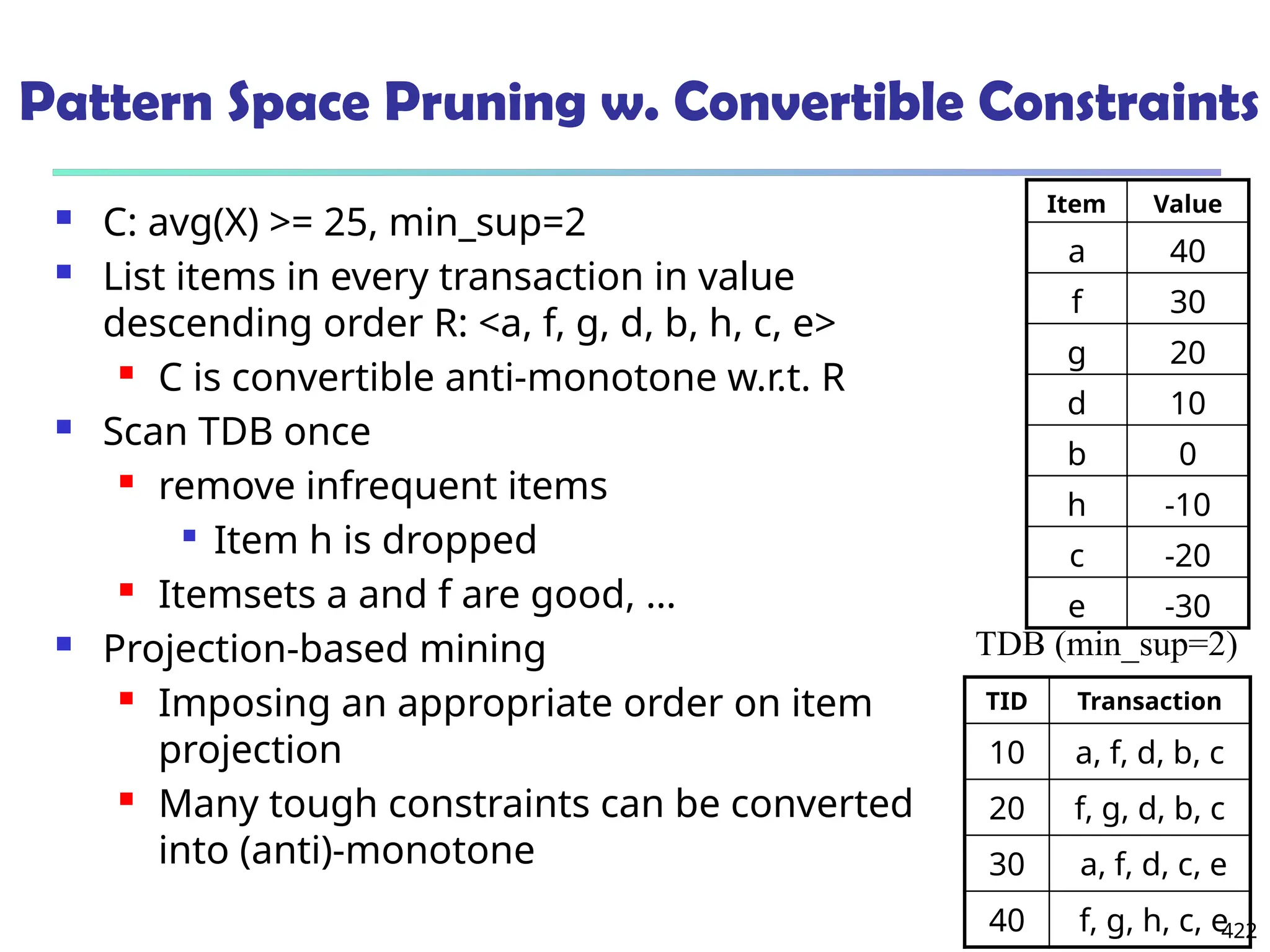

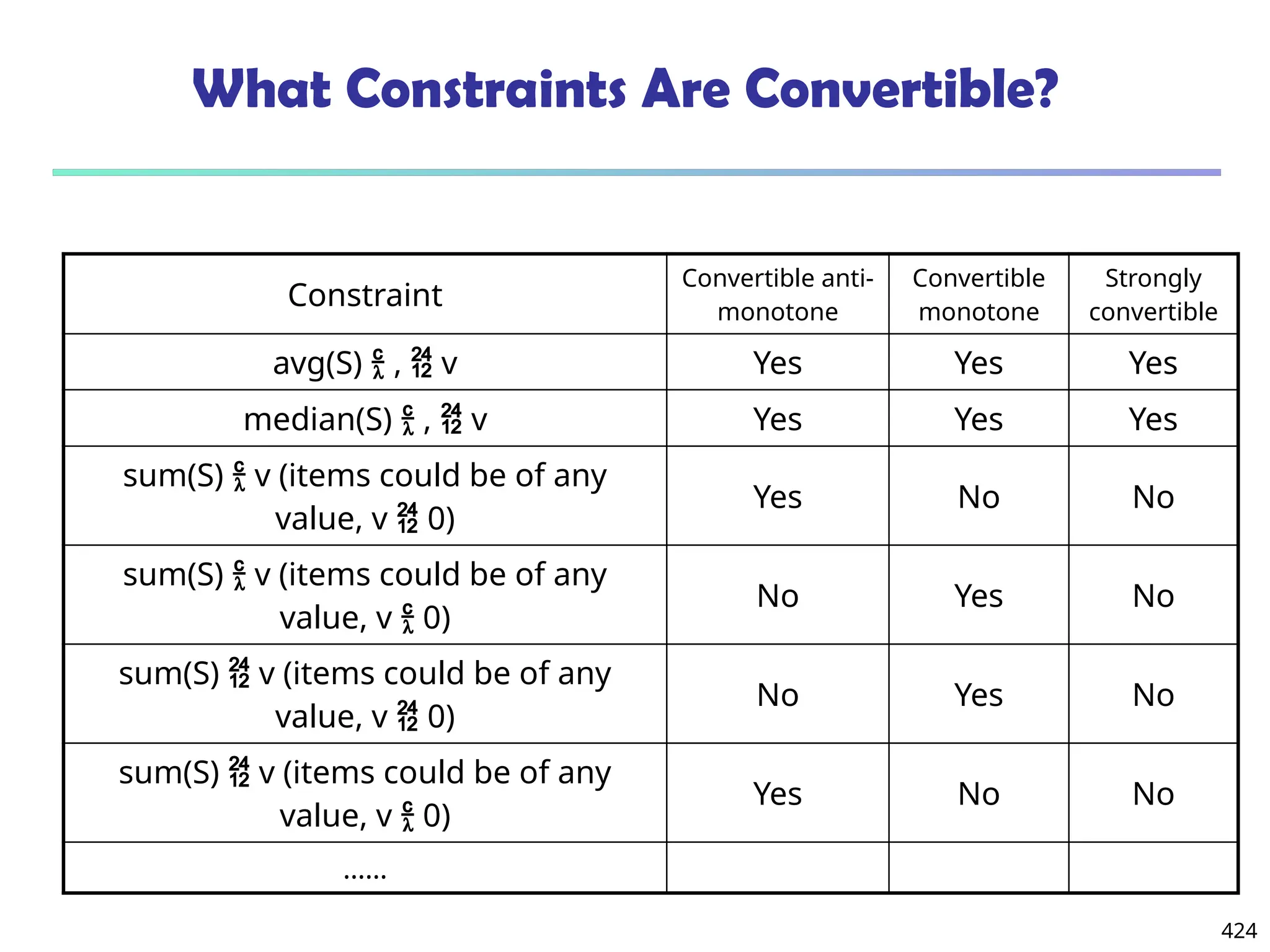
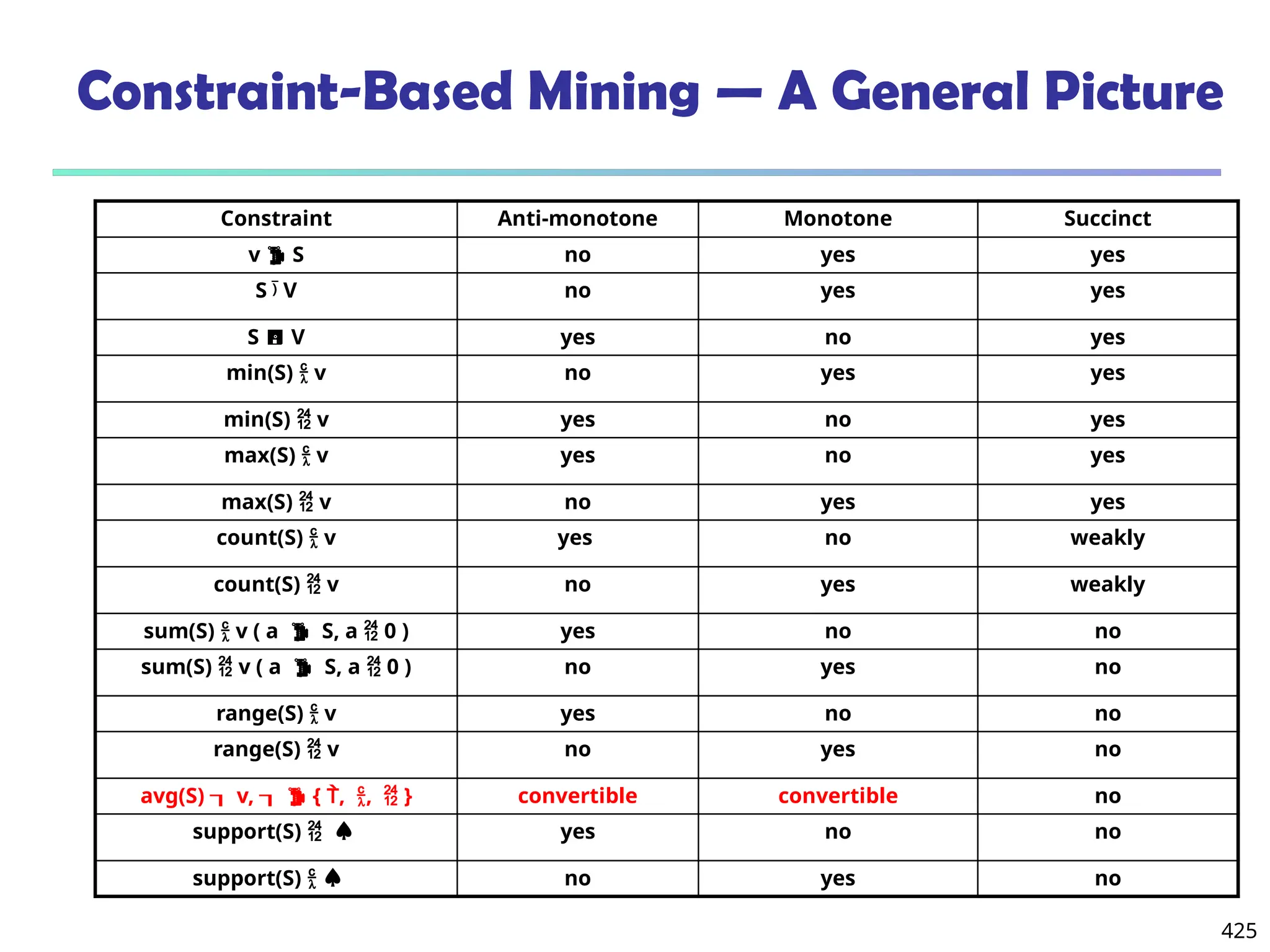



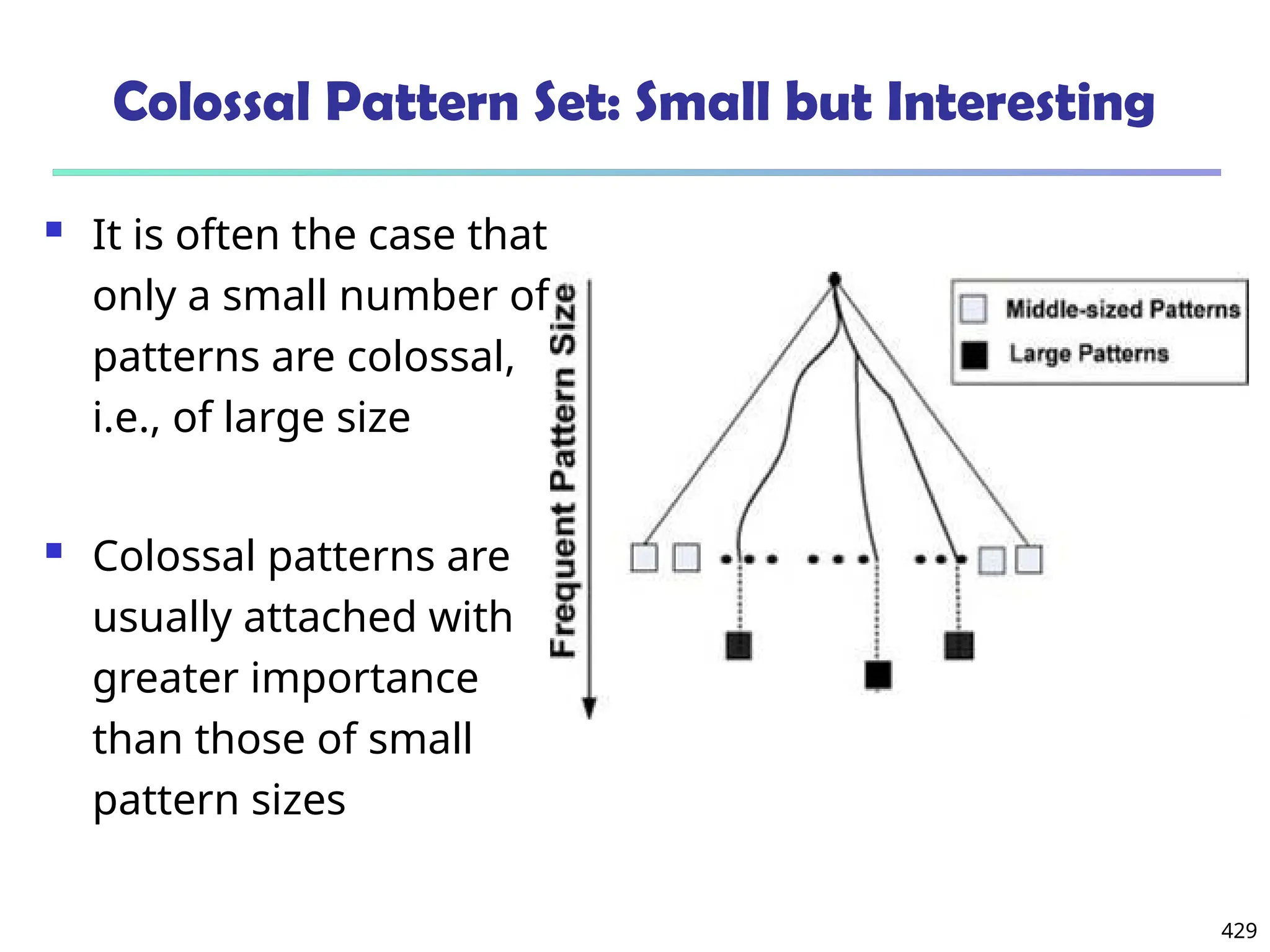



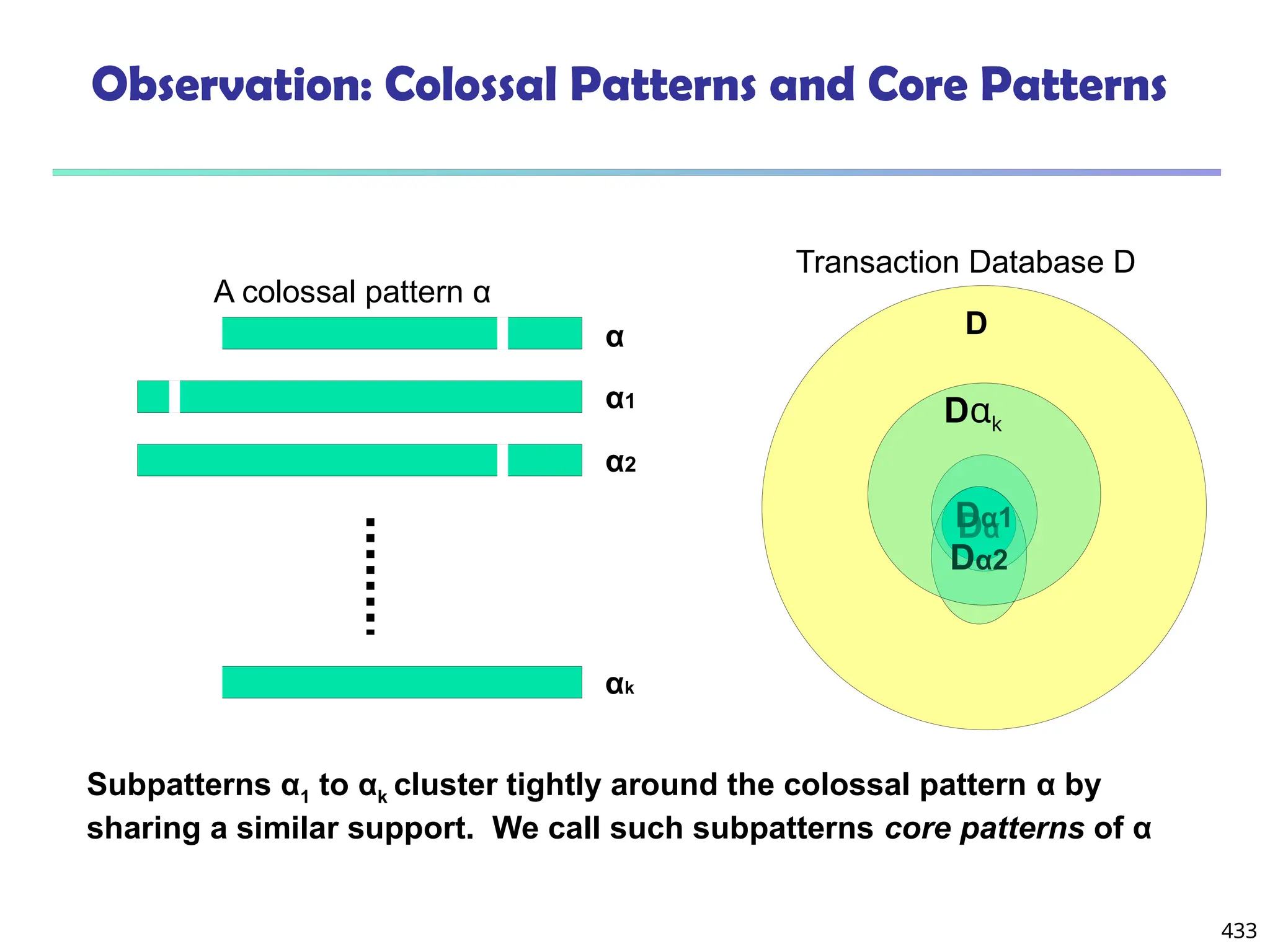


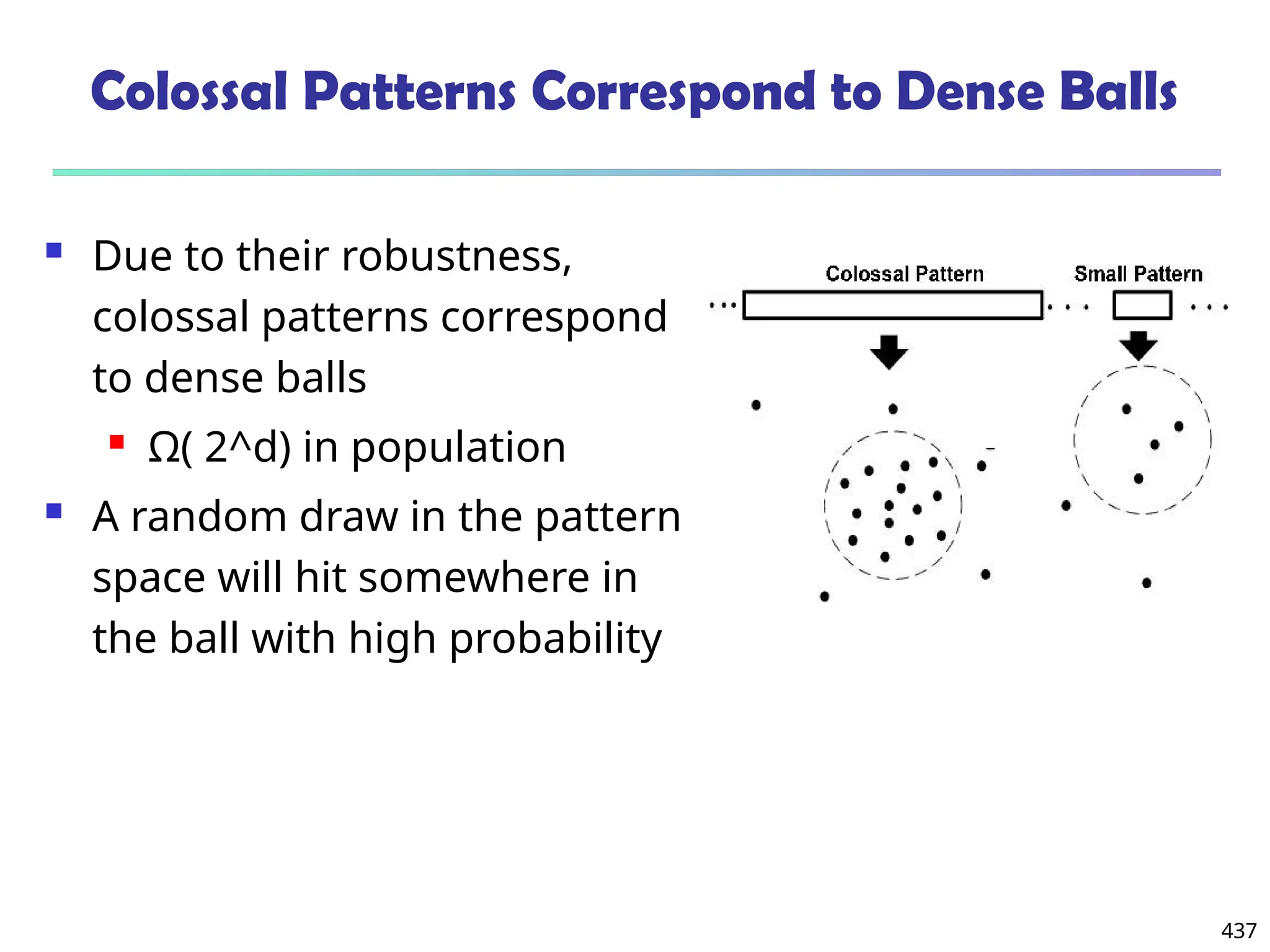













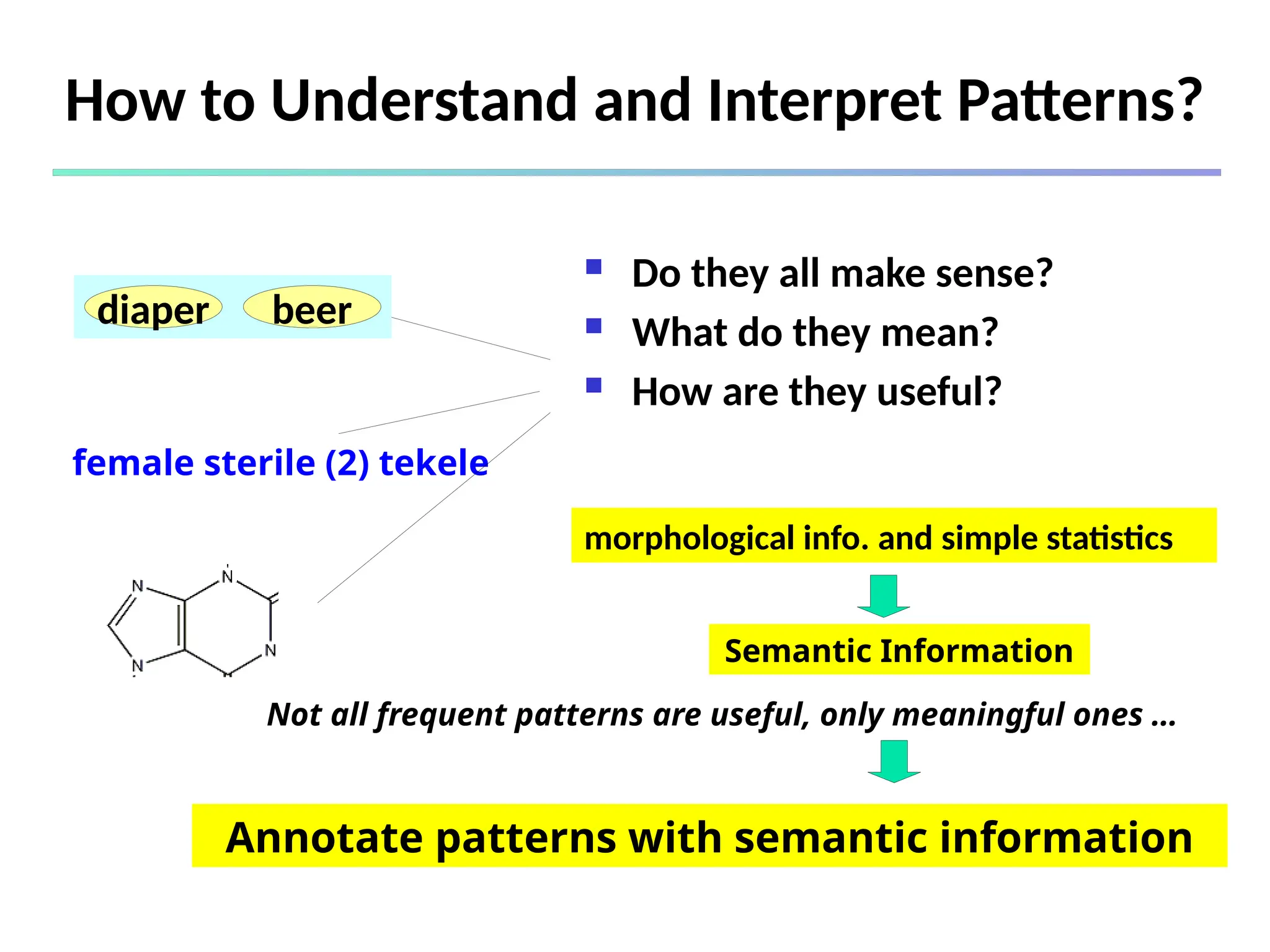


























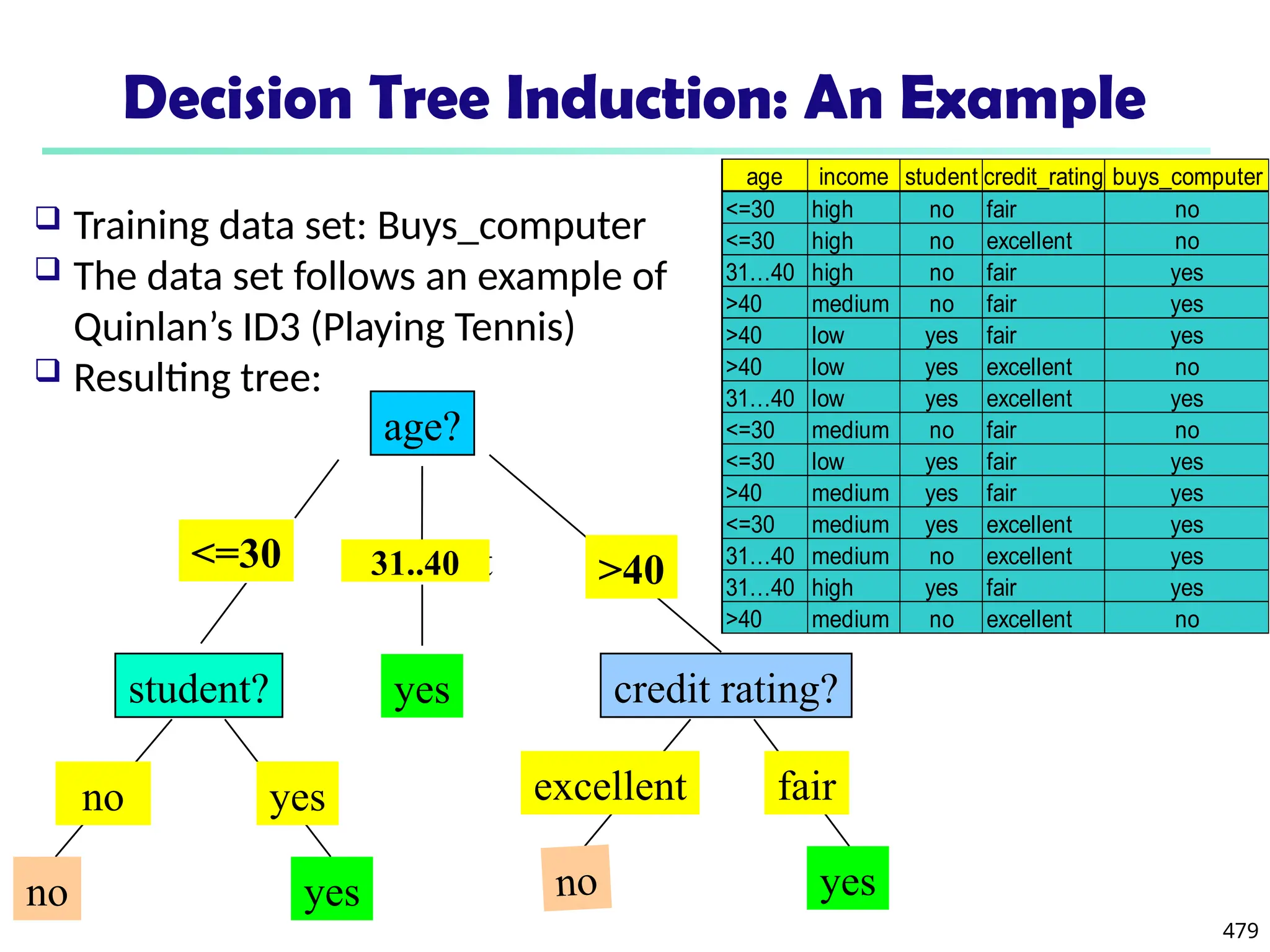






















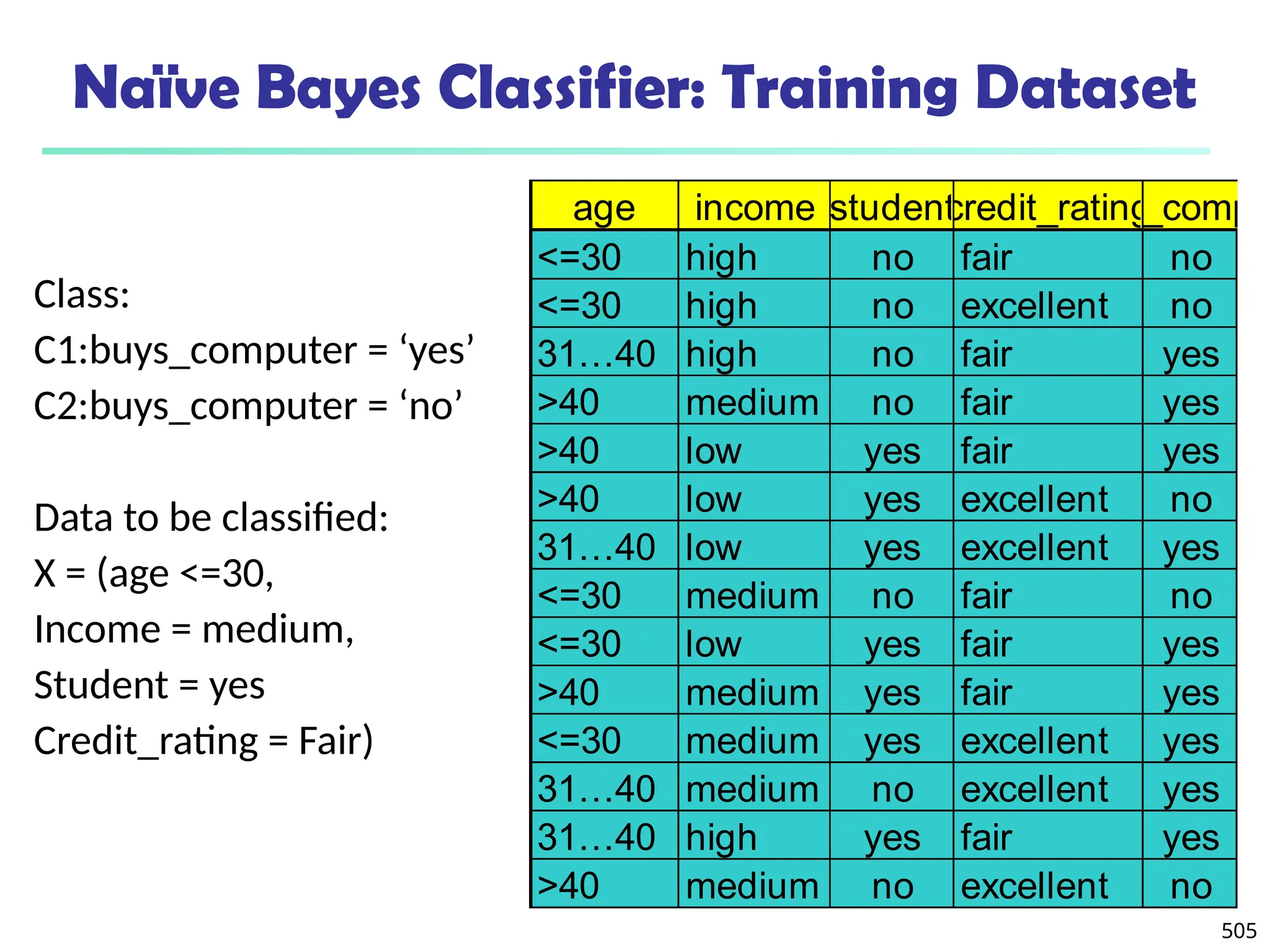







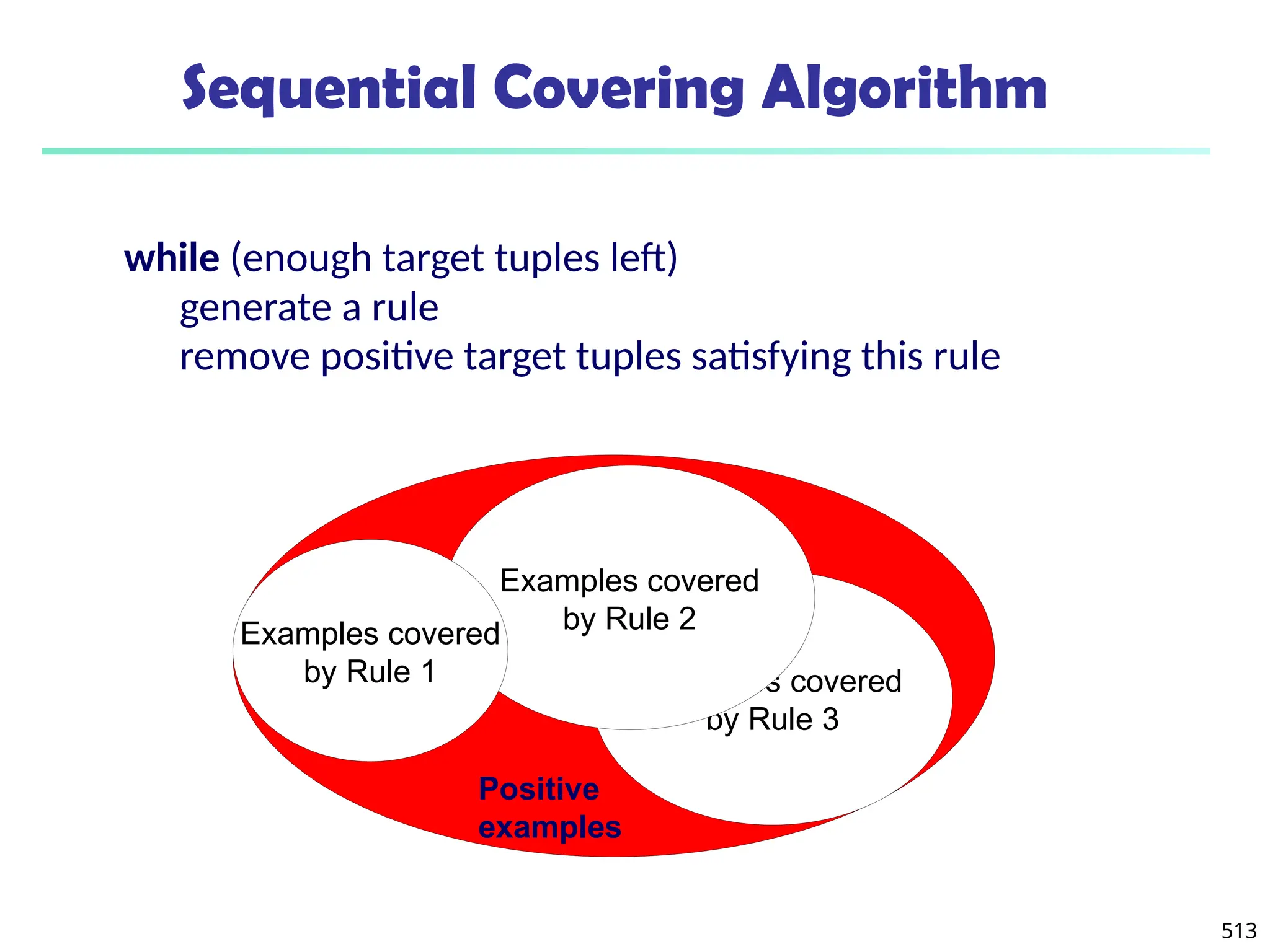




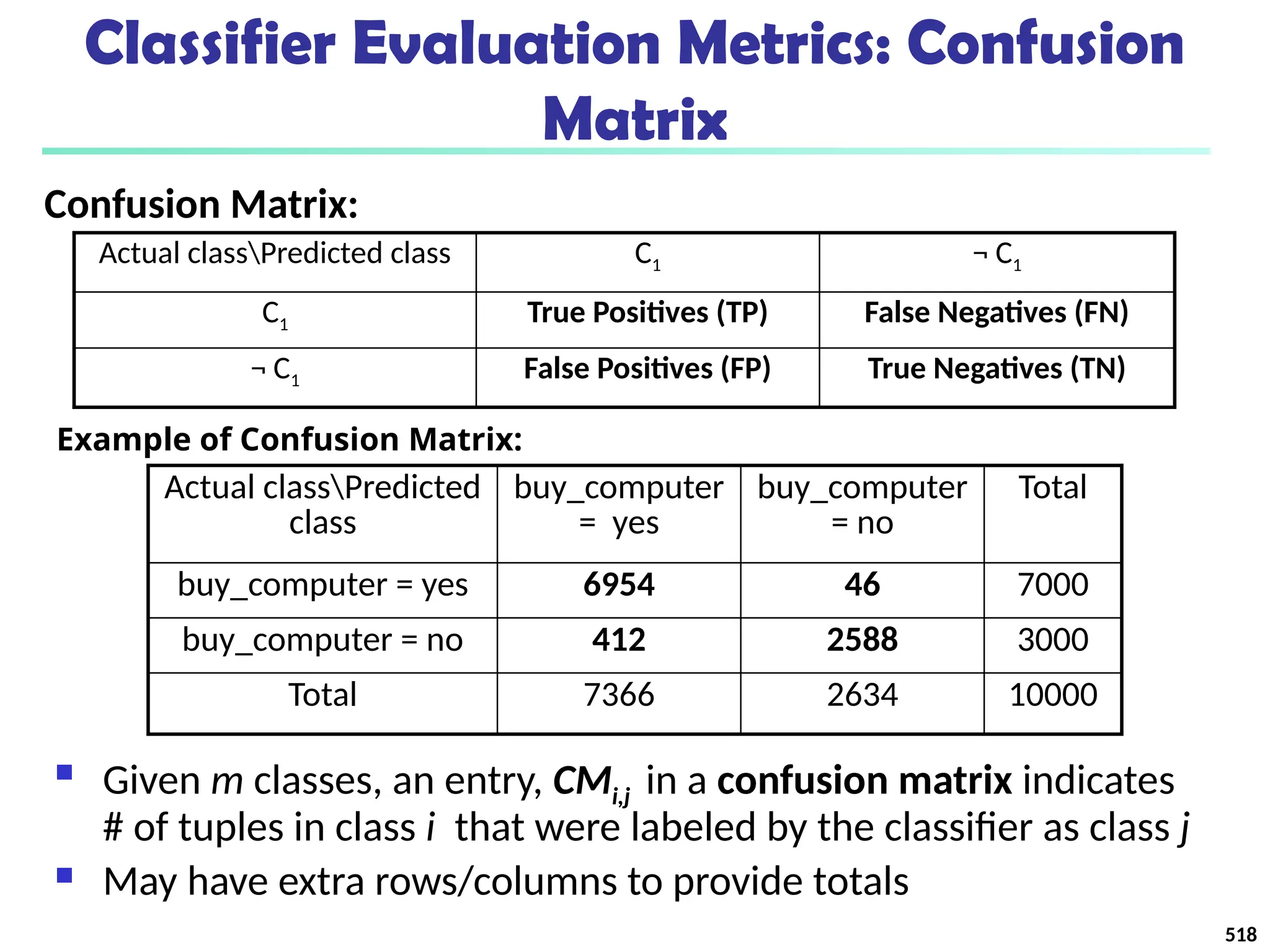


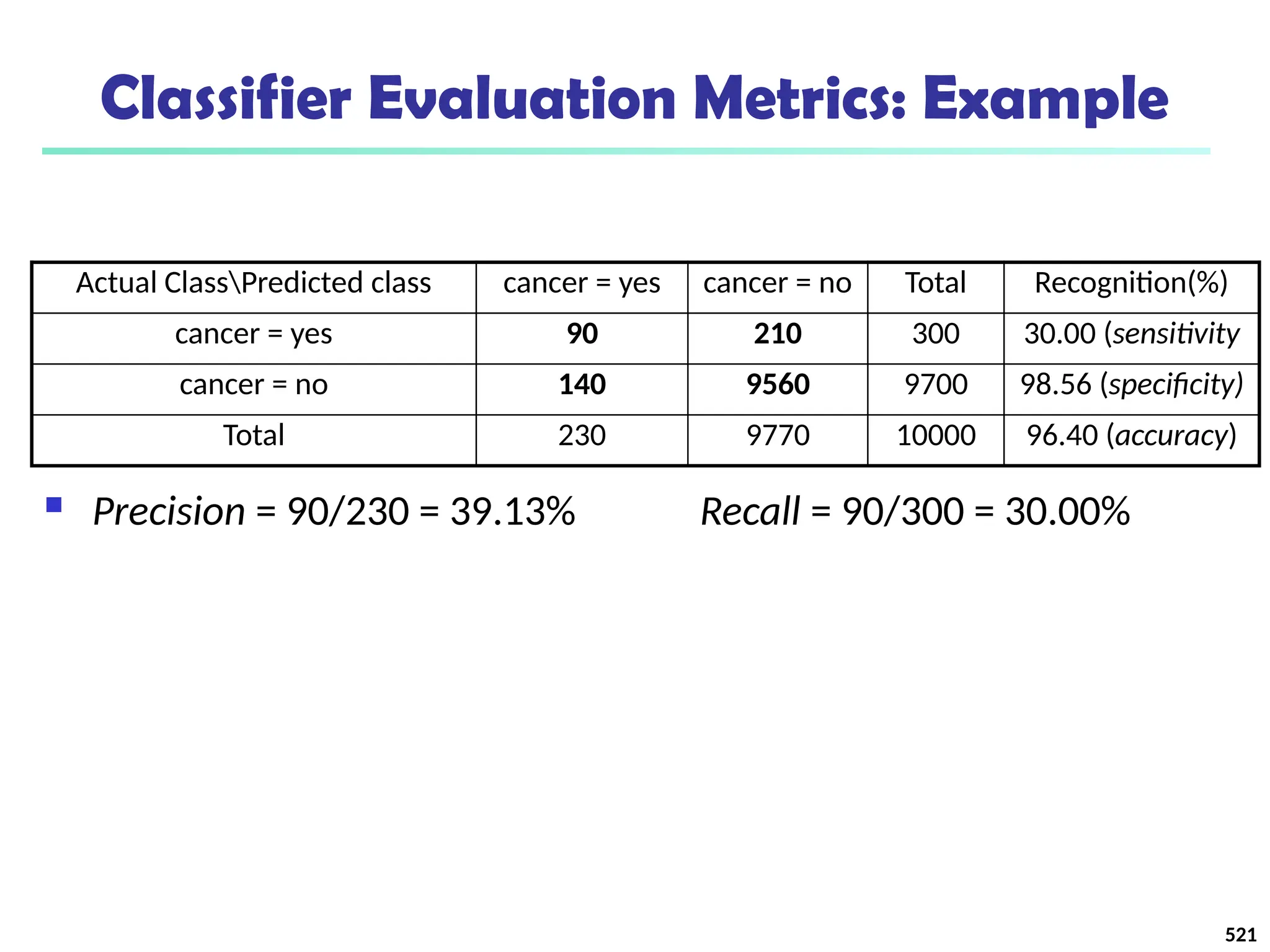





































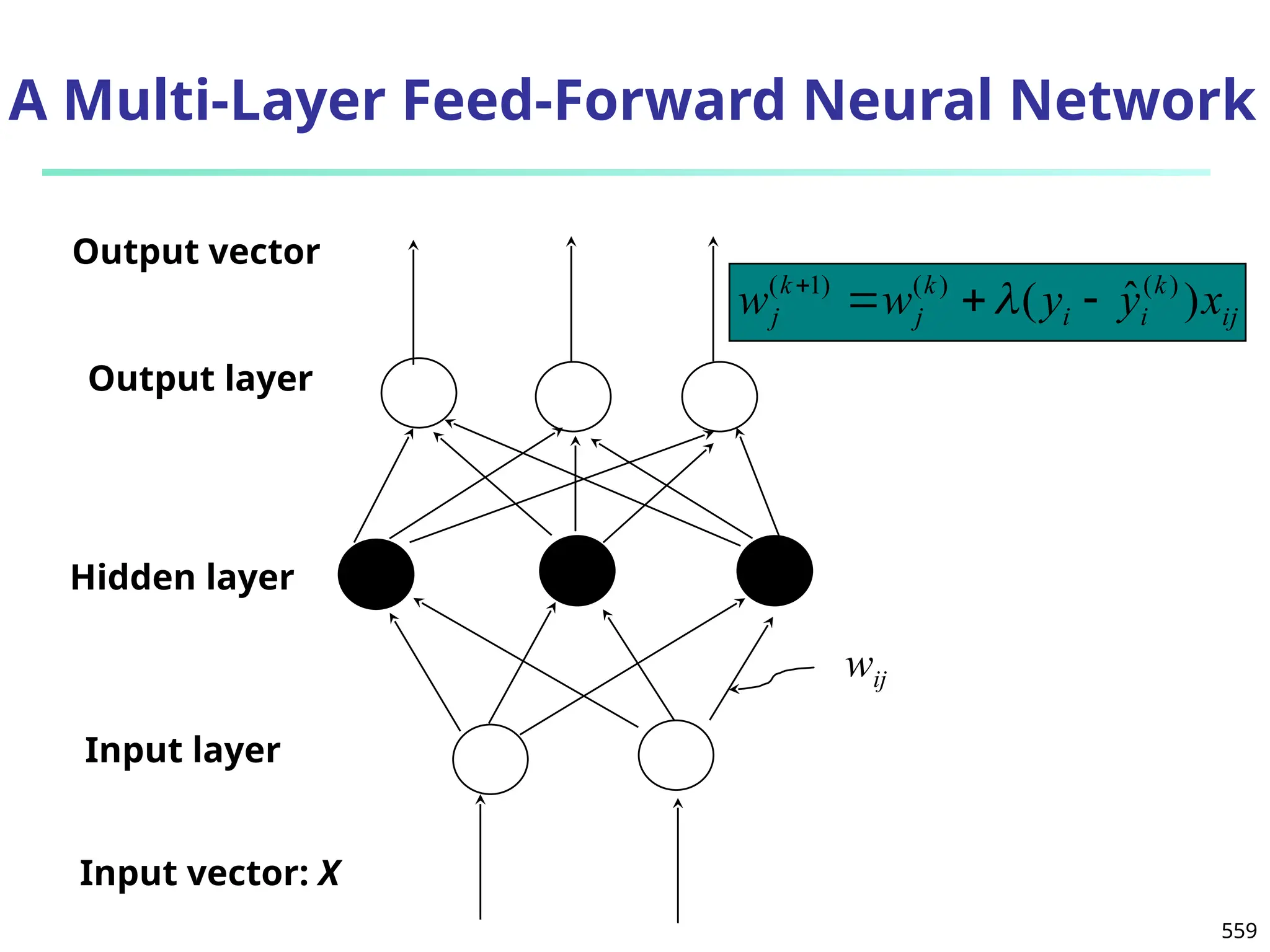

![561
Defining a Network Topology
Decide the network topology: Specify # of units in the
input layer, # of hidden layers (if > 1), # of units in each
hidden layer, and # of units in the output layer
Normalize the input values for each attribute measured
in the training tuples to [0.0—1.0]
One input unit per domain value, each initialized to 0
Output, if for classification and more than two classes,
one output unit per class is used
Once a network has been trained and its accuracy is
unacceptable, repeat the training process with a
different network topology or a different set of initial
weights](https://image.slidesharecdn.com/dwdm3rdeditiontextbookslides-241024155956-ed696a42/75/DWDM-3rd-EDITION-TEXT-BOOK-SLIDES24-pptx-560-2048.jpg)








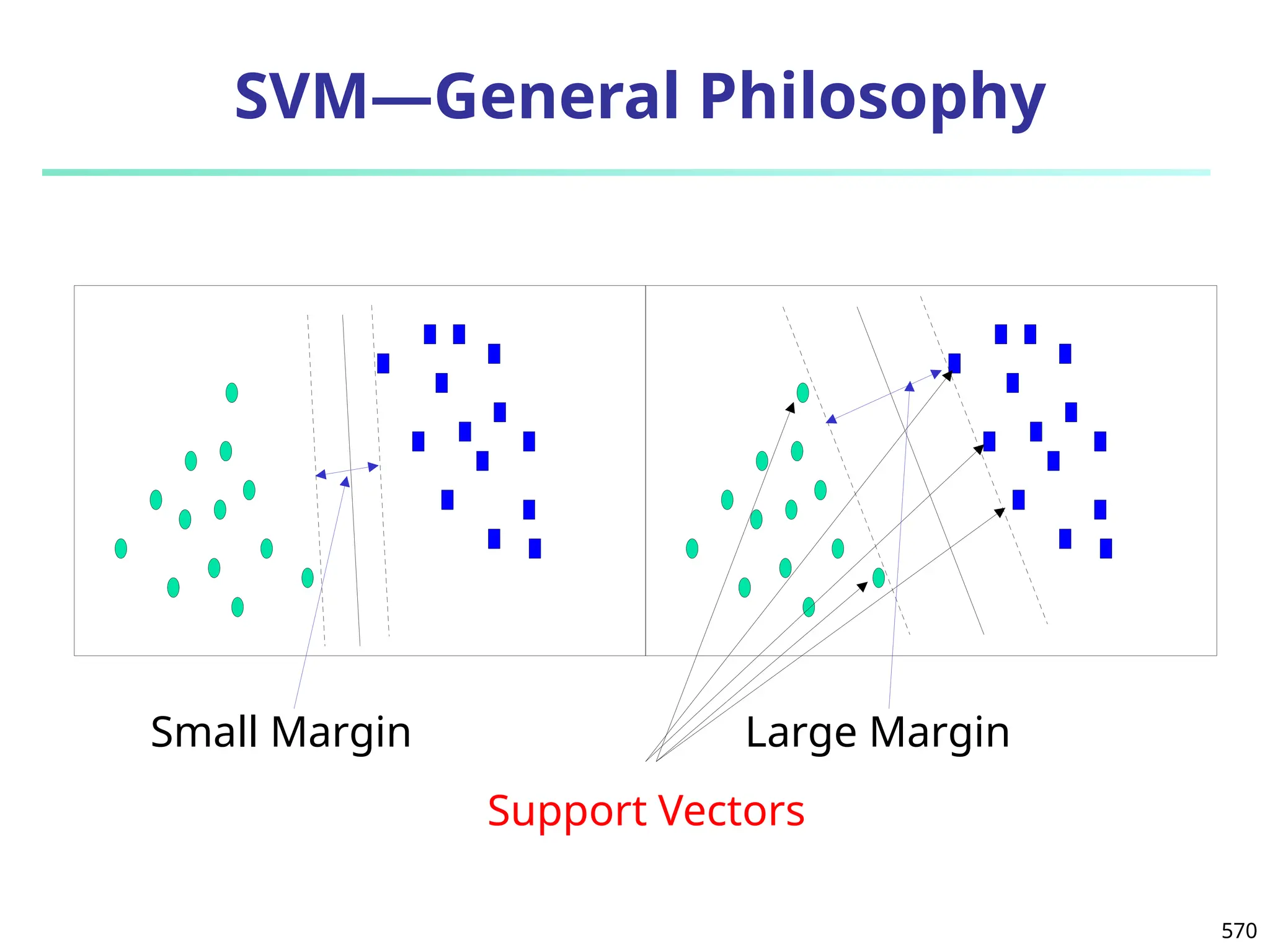







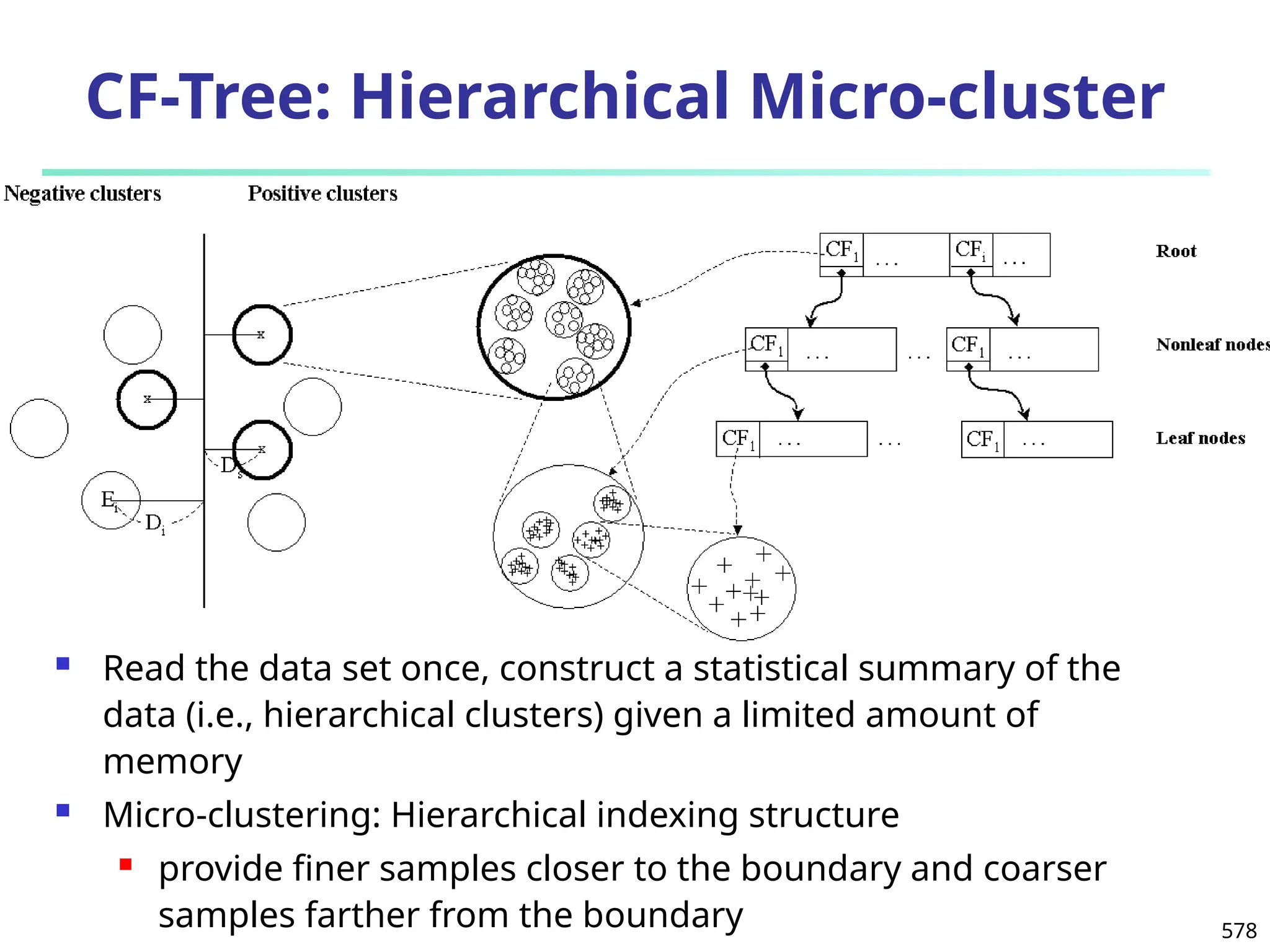
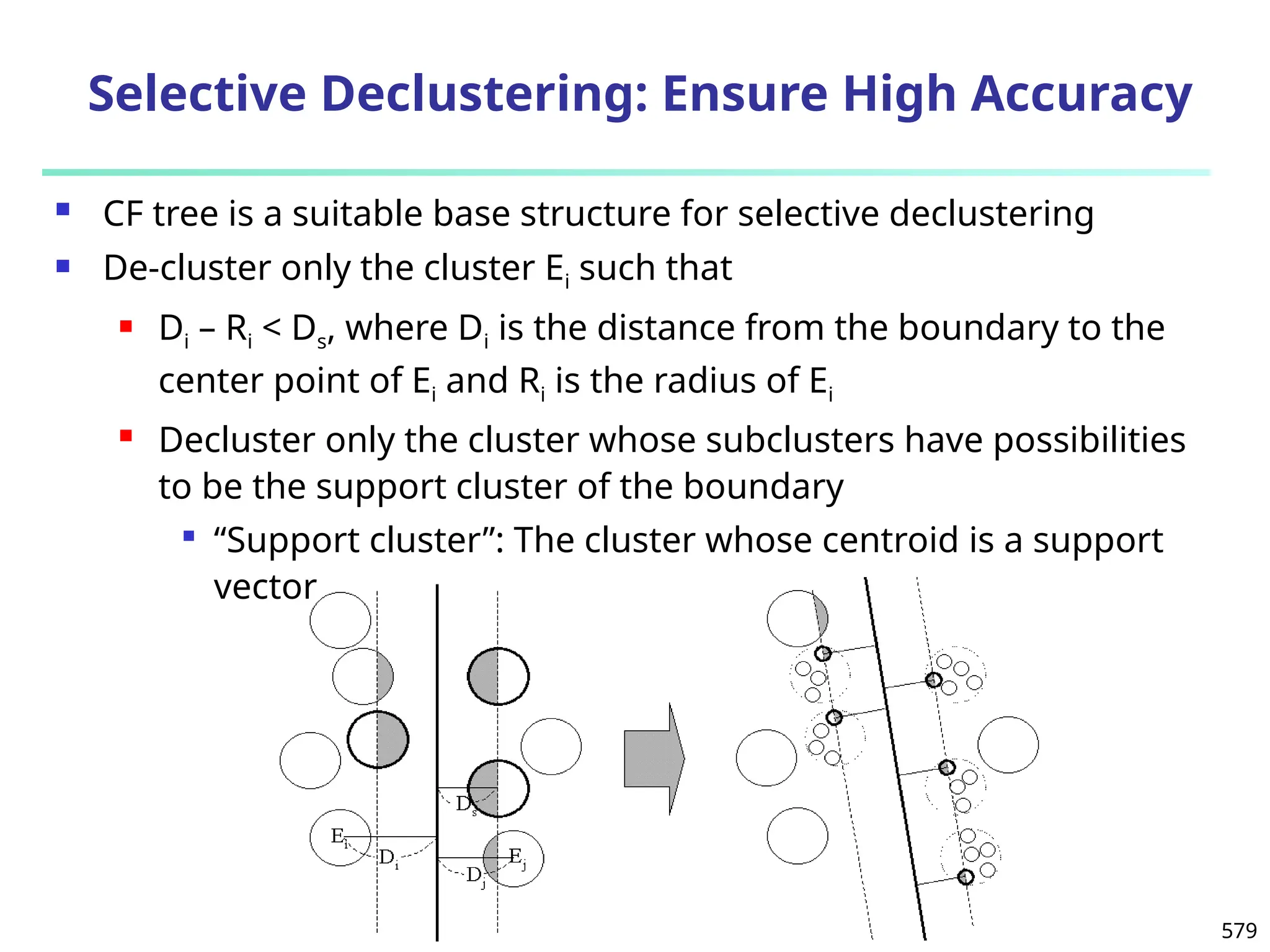

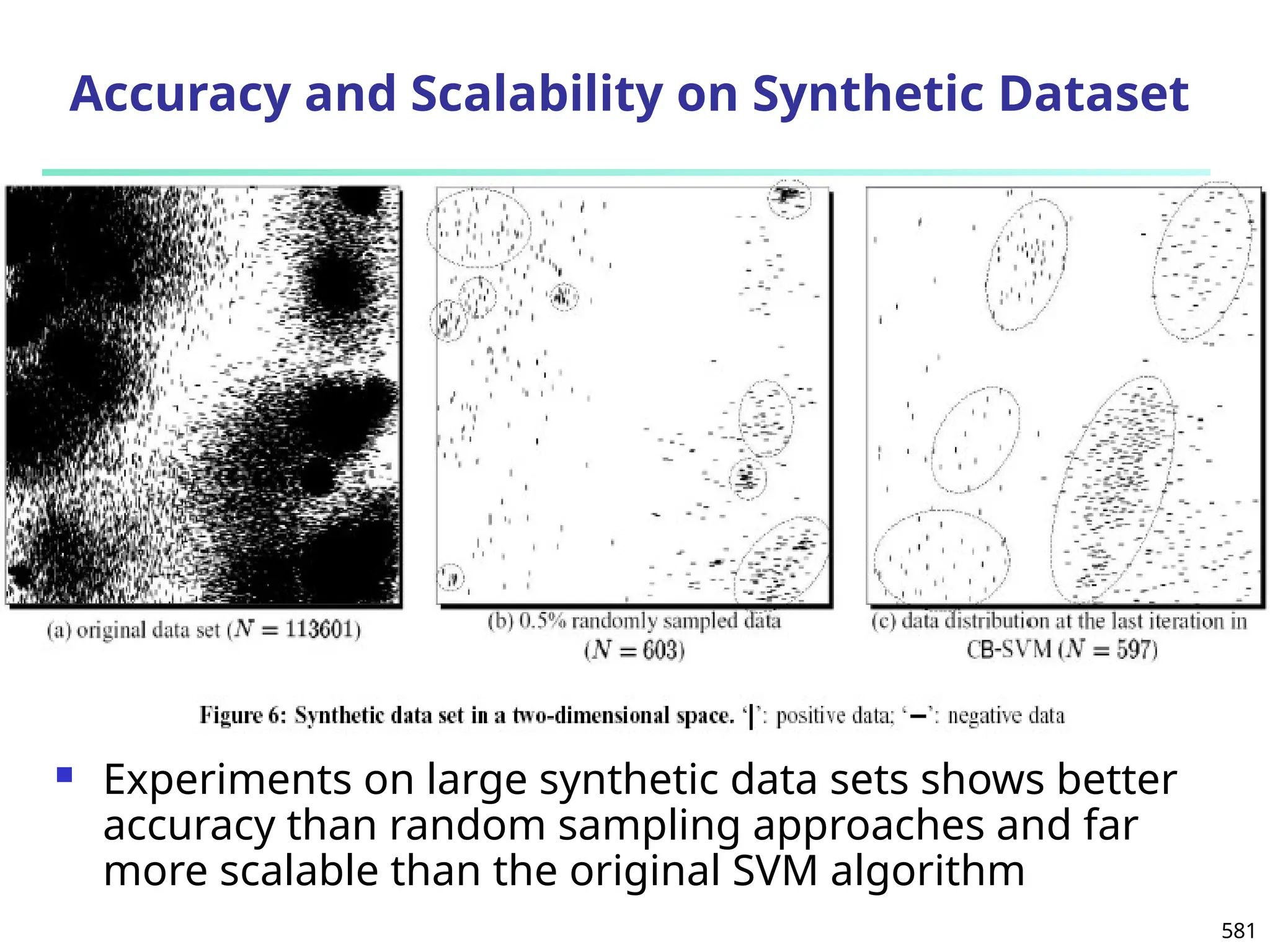






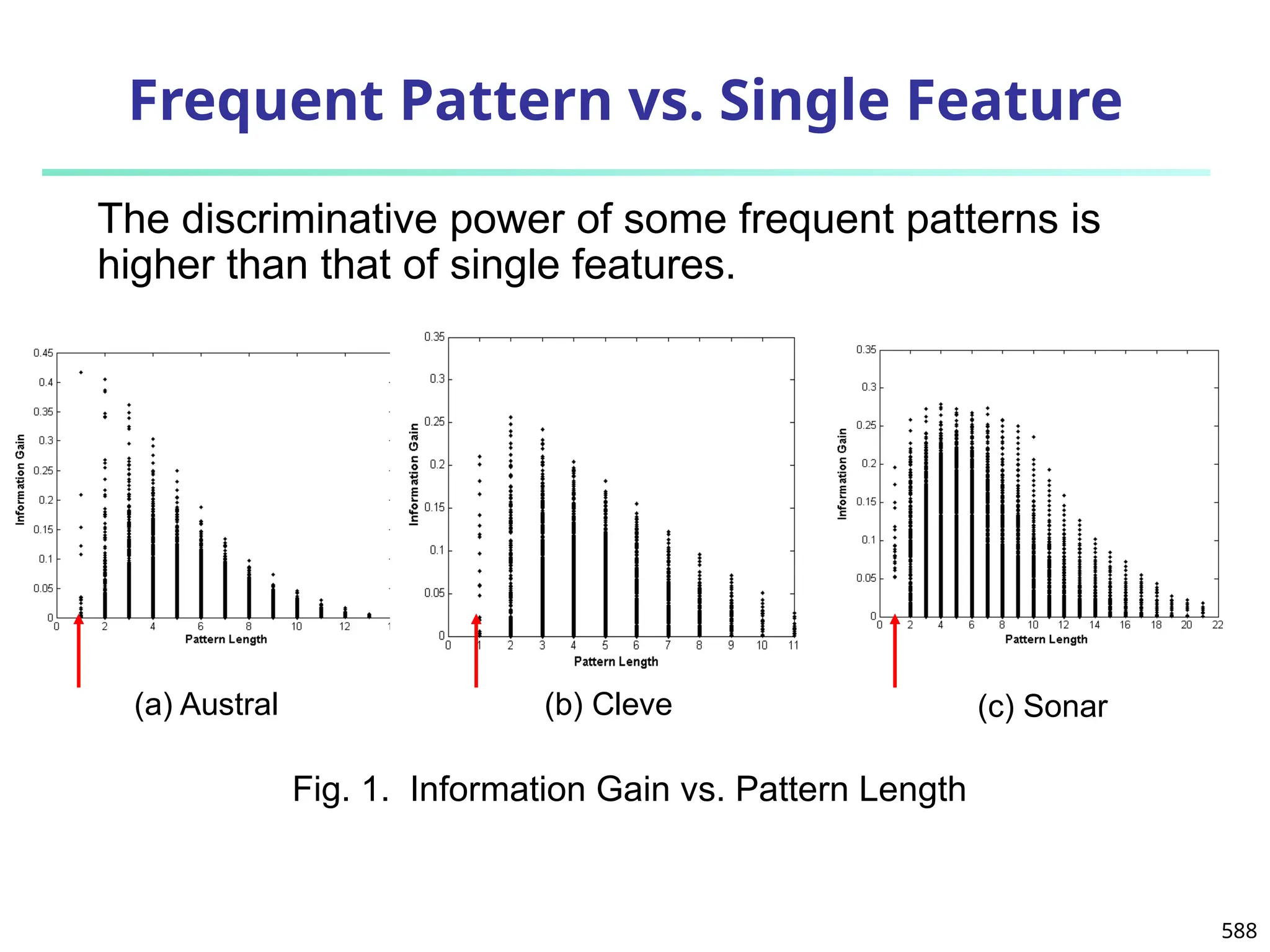


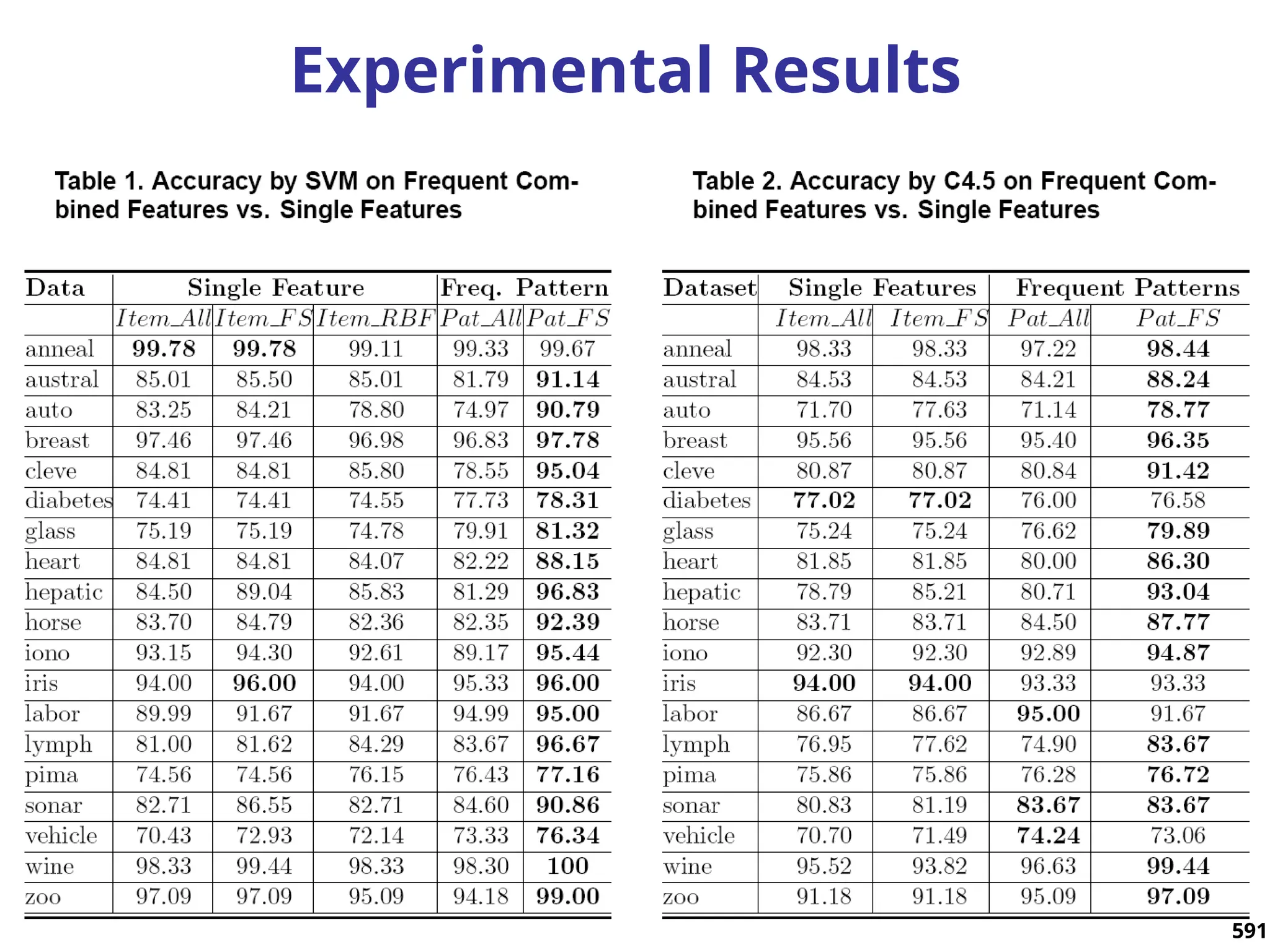

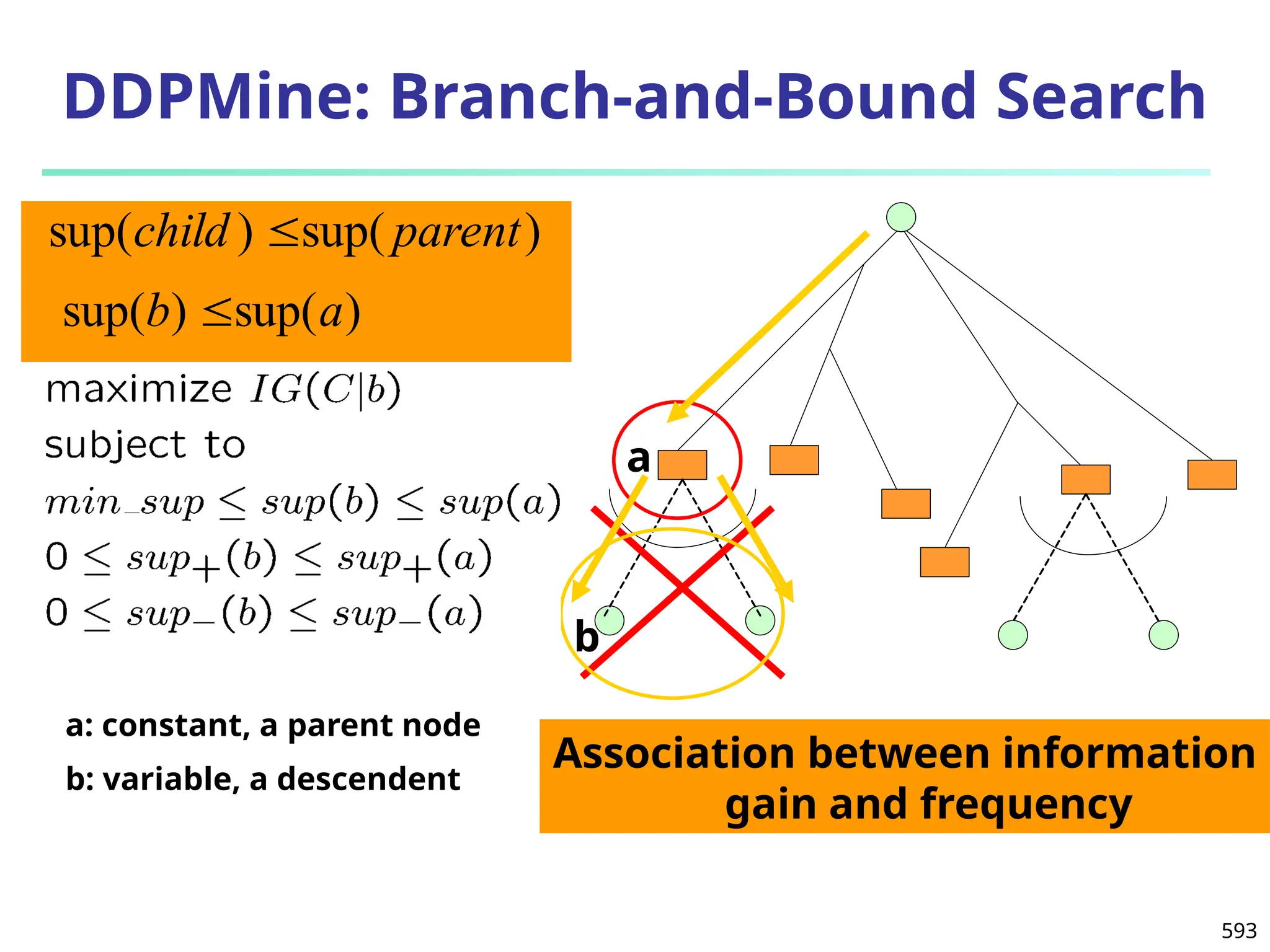
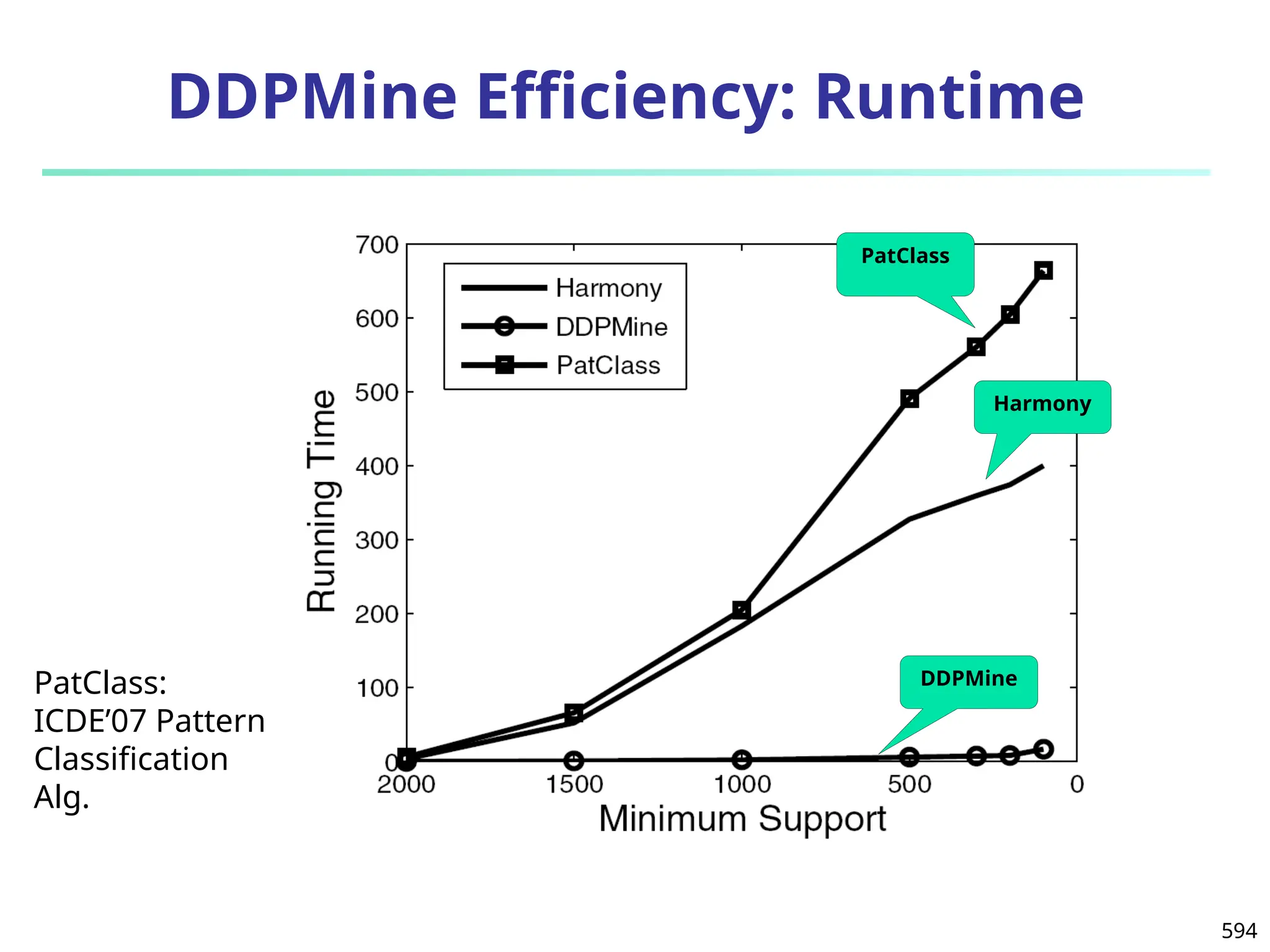












![Error-Correcting Codes for Multiclass Classification
Originally designed to correct errors during
data transmission for communication tasks by
exploring data redundancy
Example
A 7-bit codeword associated with classes 1-4
607
Class Error-Corr.
Codeword
C1 1 1 1 1 1 1 1
C2 0 0 0 0 1 1 1
C3 0 0 1 1 0 0 1
C4 0 1 0 1 0 1 0
Given a unknown tuple X, the 7-trained classifiers output:
0001010
Hamming distance: # of different bits between two codewords
H(X, C1) = 5, by checking # of bits between [1111111] & [0001010]
H(X, C2) = 3, H(X, C3) = 3, H(X, C4) = 1, thus C4 as the label for X
Error-correcting codes can correct up to (h-1)/h 1-bit error, where h
is the minimum Hamming distance between any two codewords
If we use 1-bit per class, it is equiv. to one-vs.-all approach, the code
are insufficient to self-correct
When selecting error-correcting codes, there should be good row-
wise and col.-wise separation between the codewords](https://image.slidesharecdn.com/dwdm3rdeditiontextbookslides-241024155956-ed696a42/75/DWDM-3rd-EDITION-TEXT-BOOK-SLIDES24-pptx-606-2048.jpg)































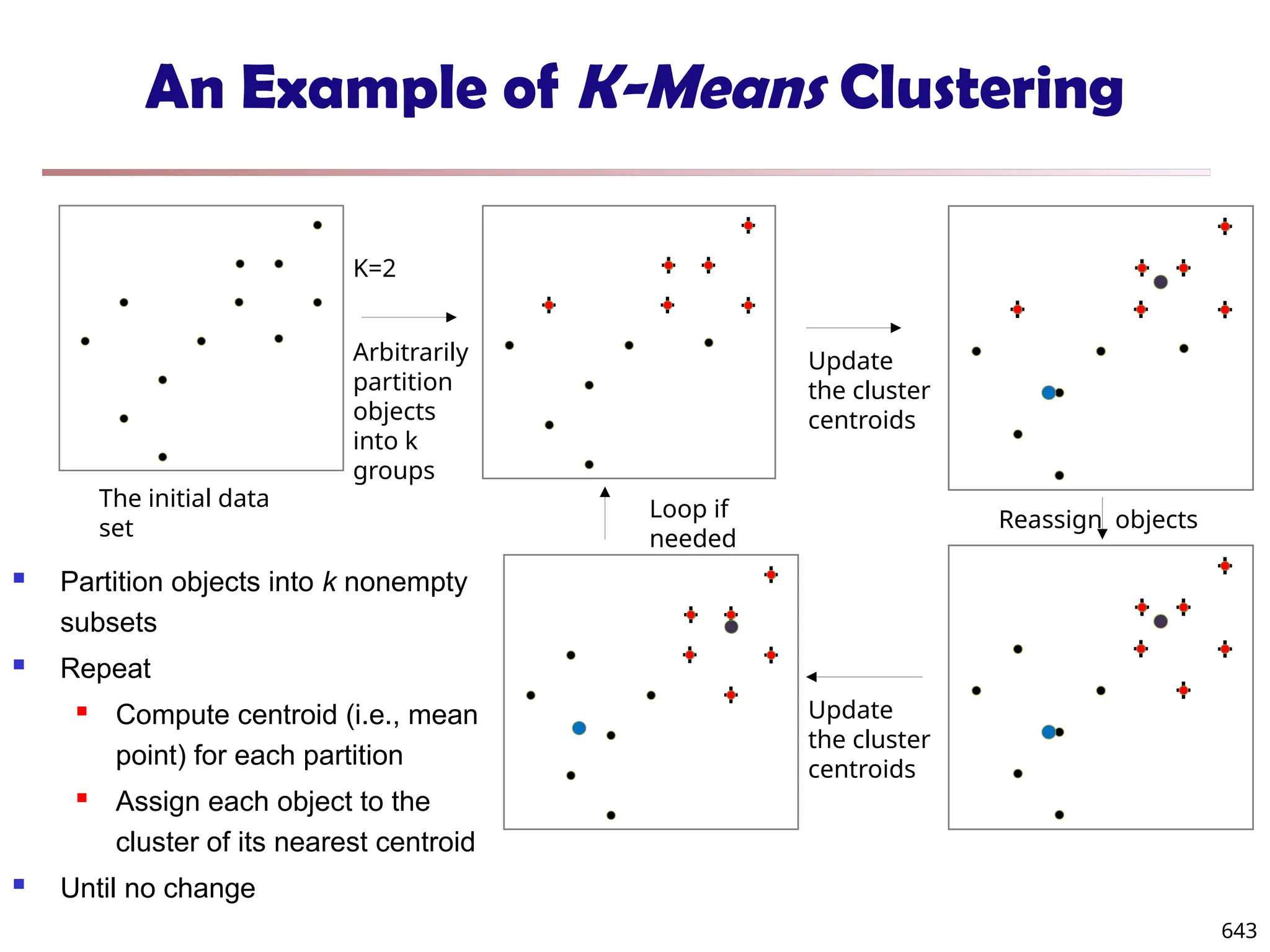



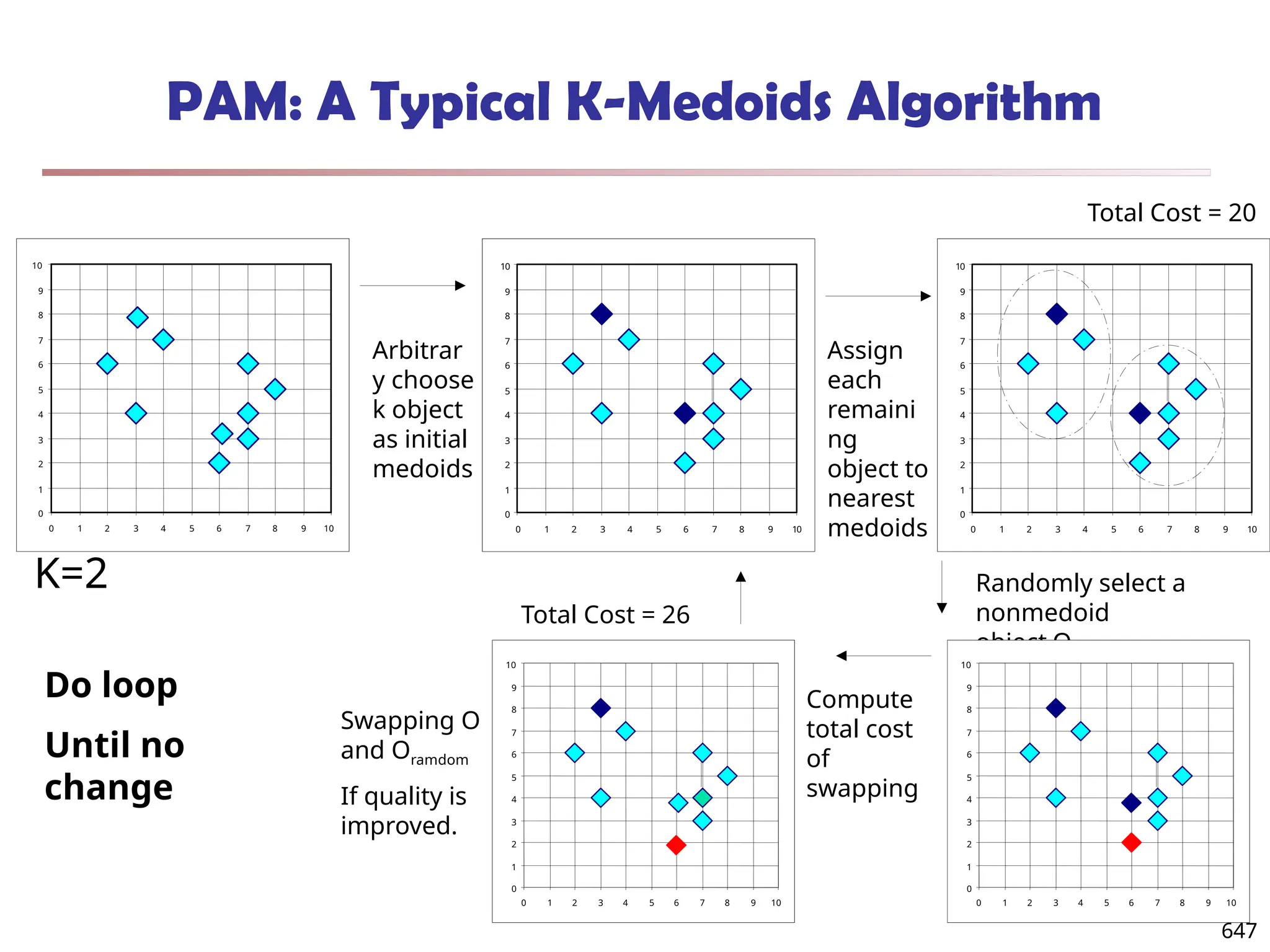


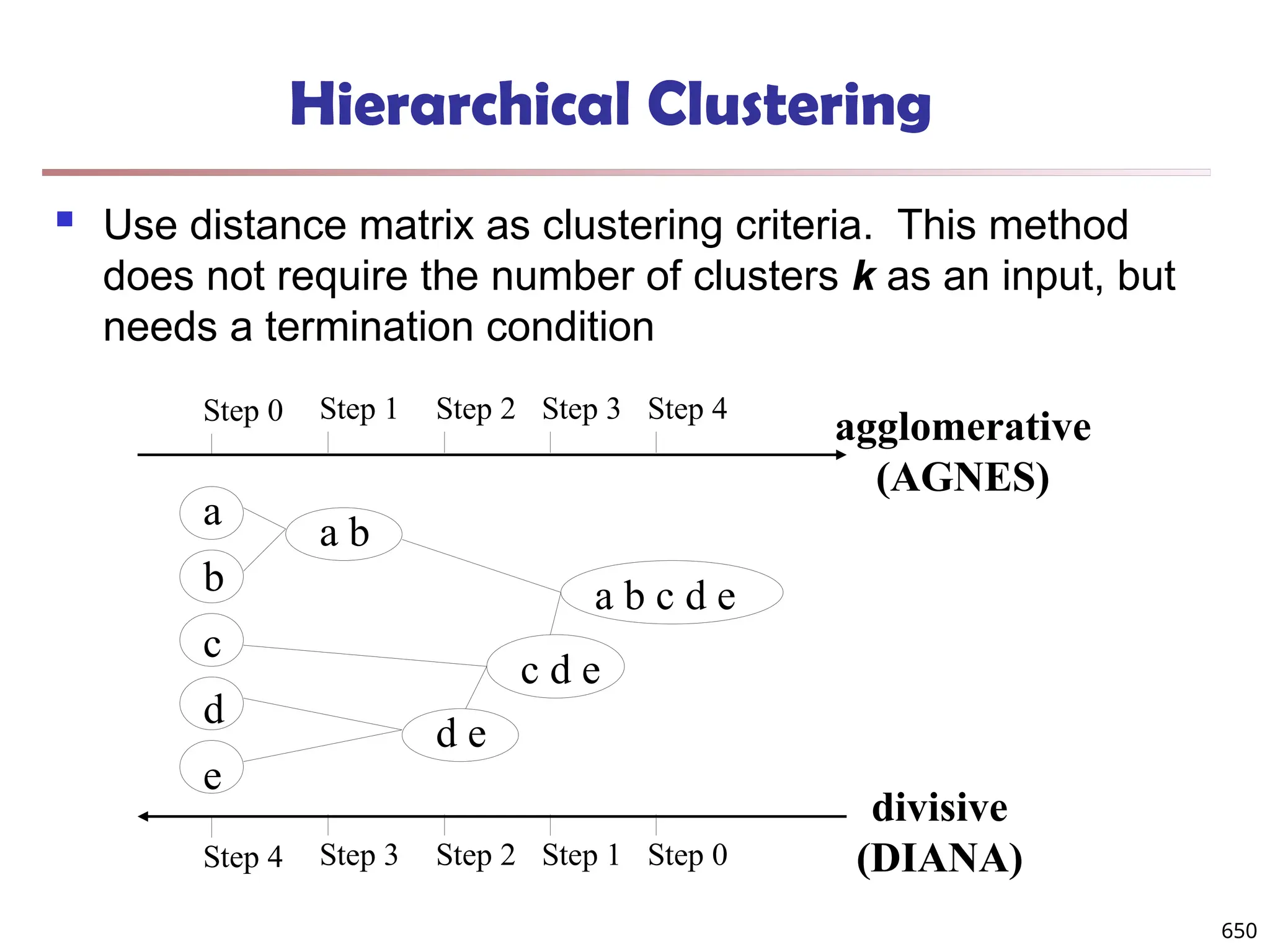

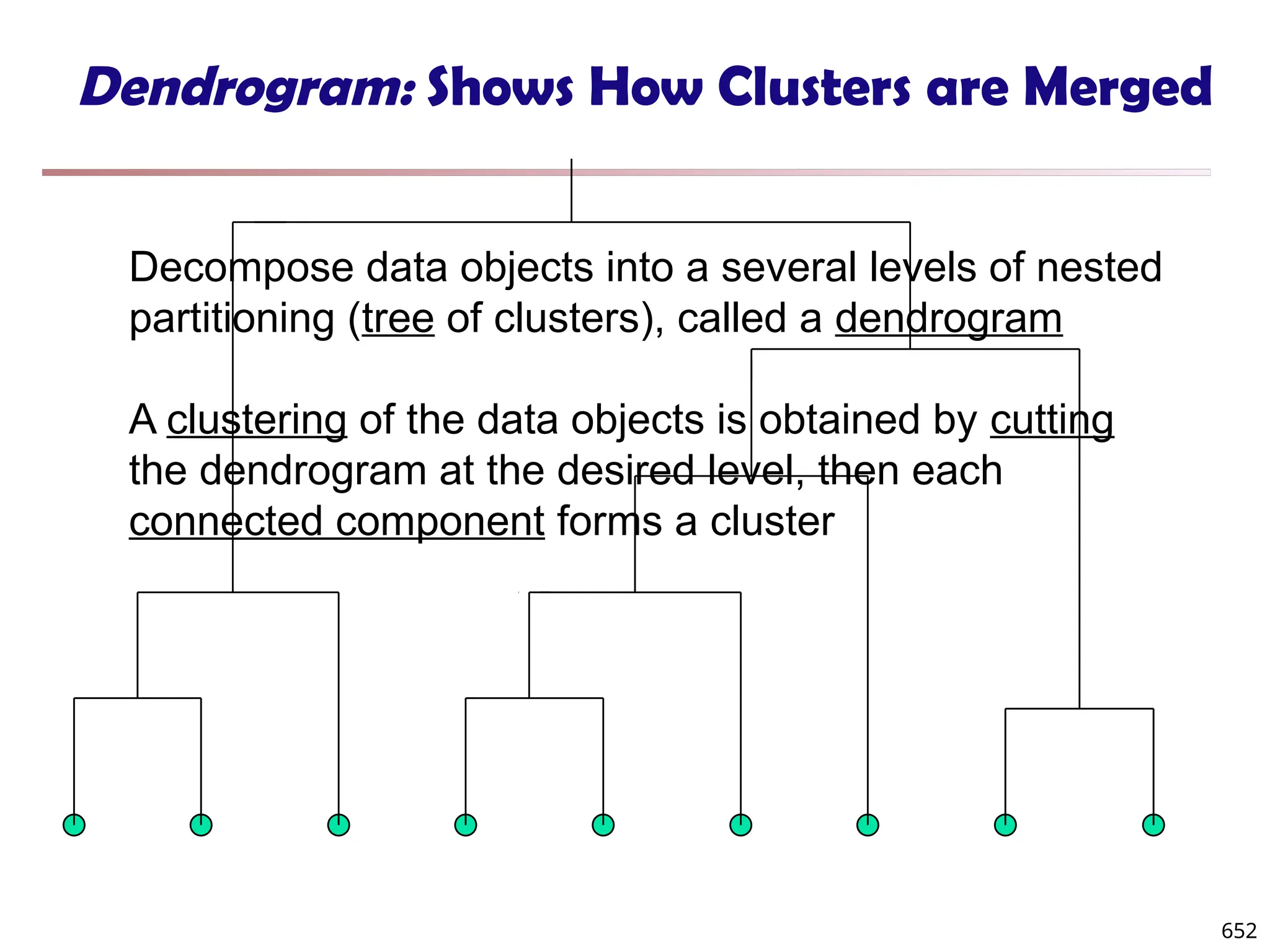
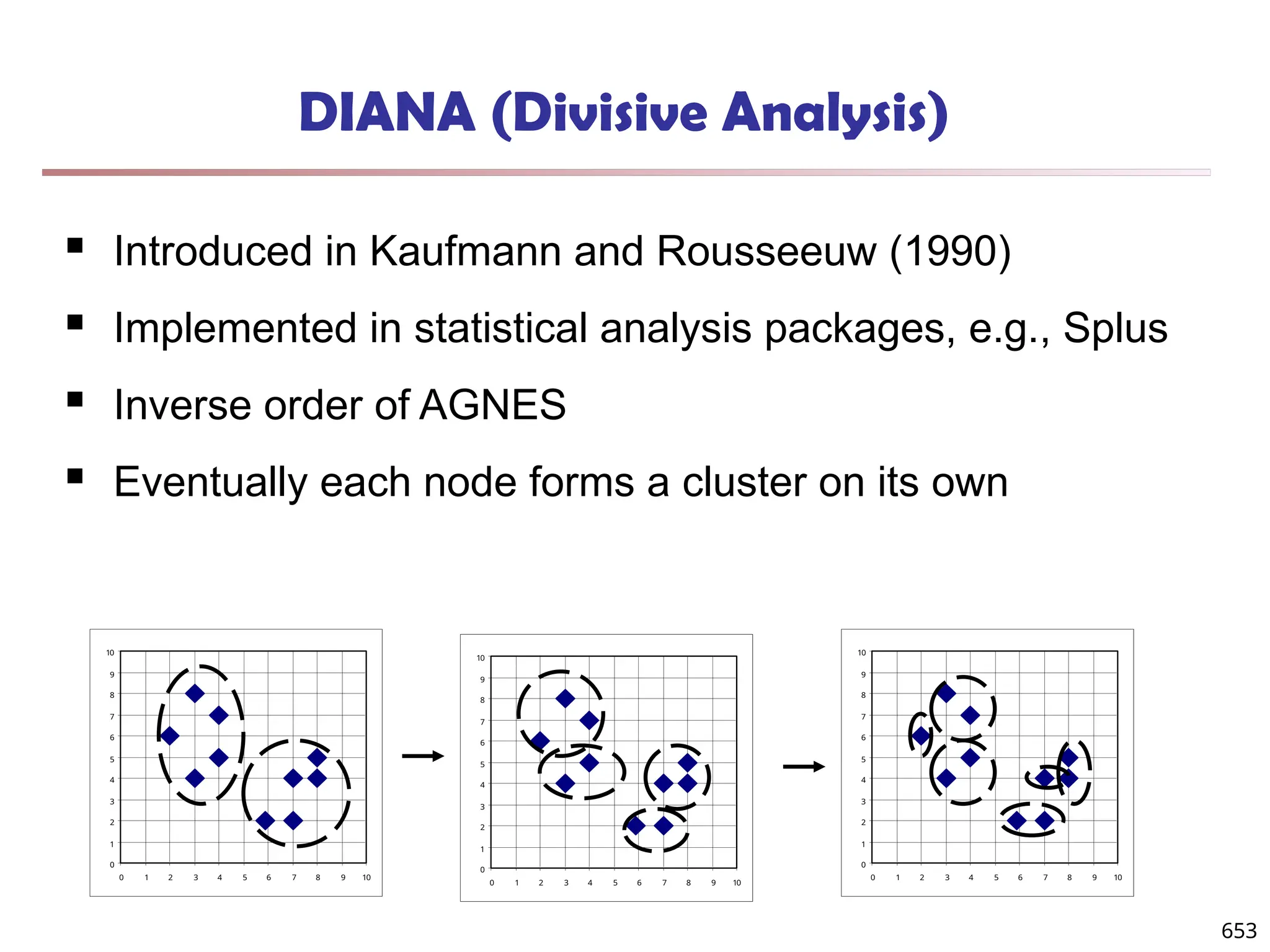




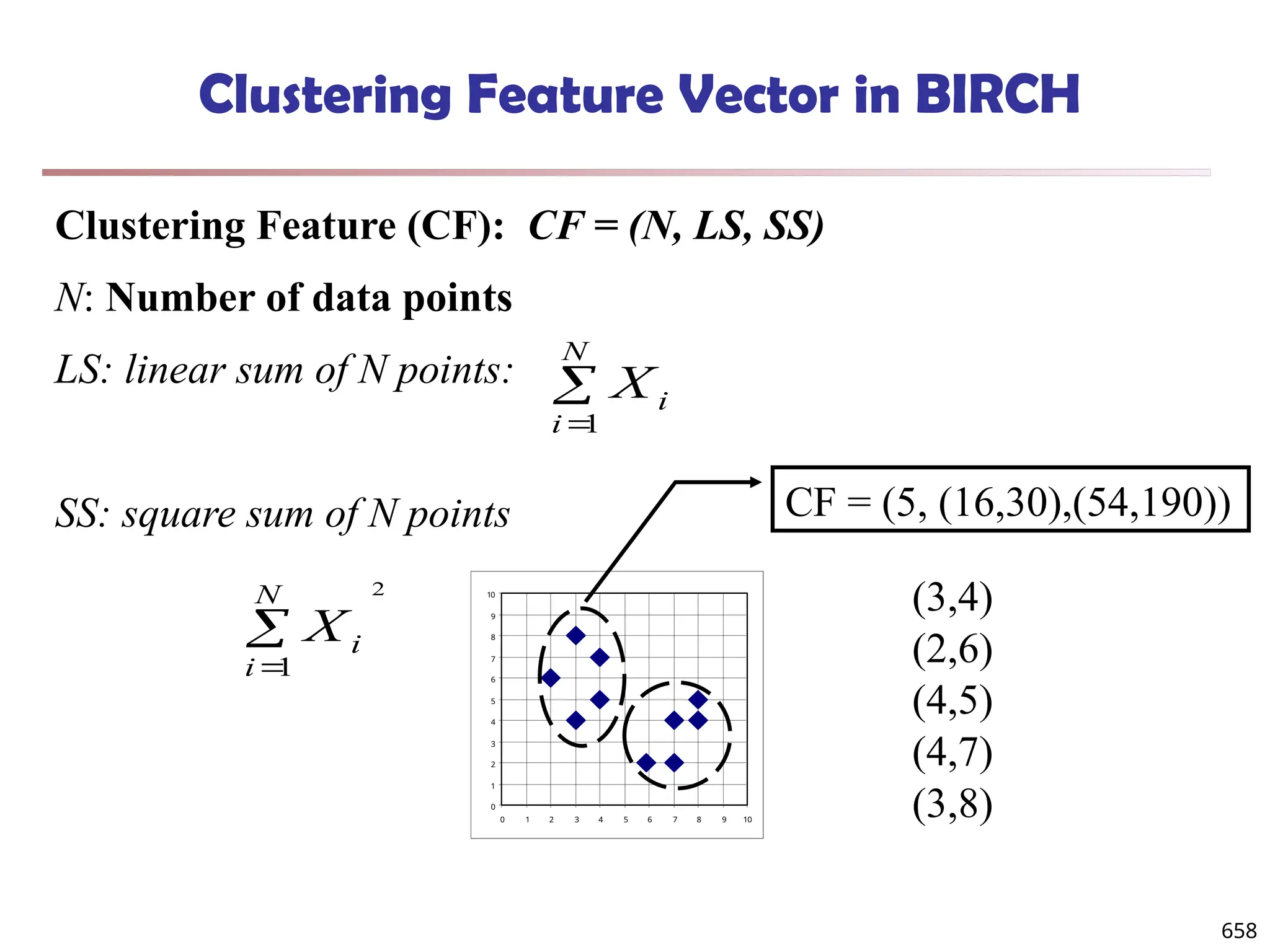

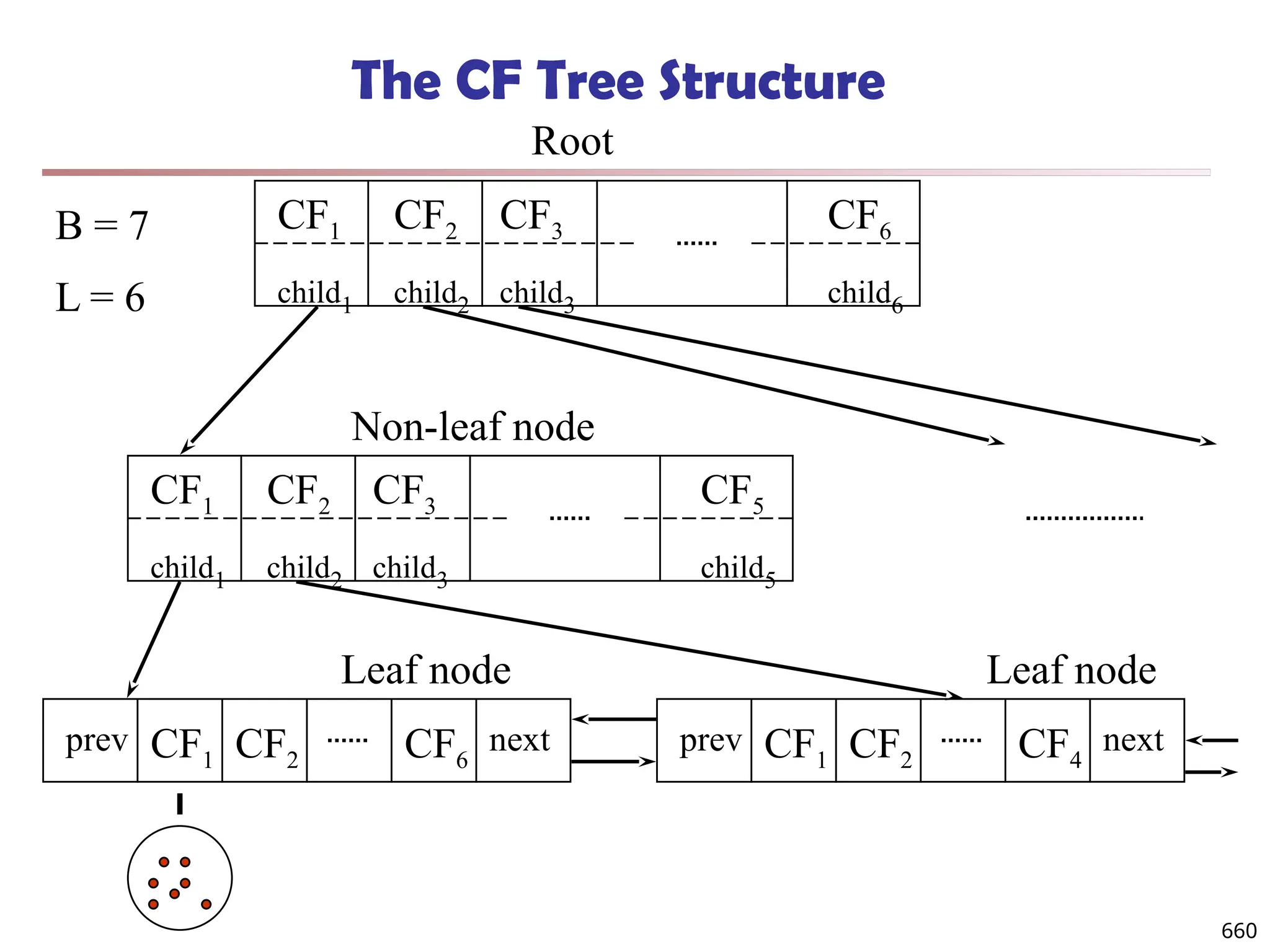


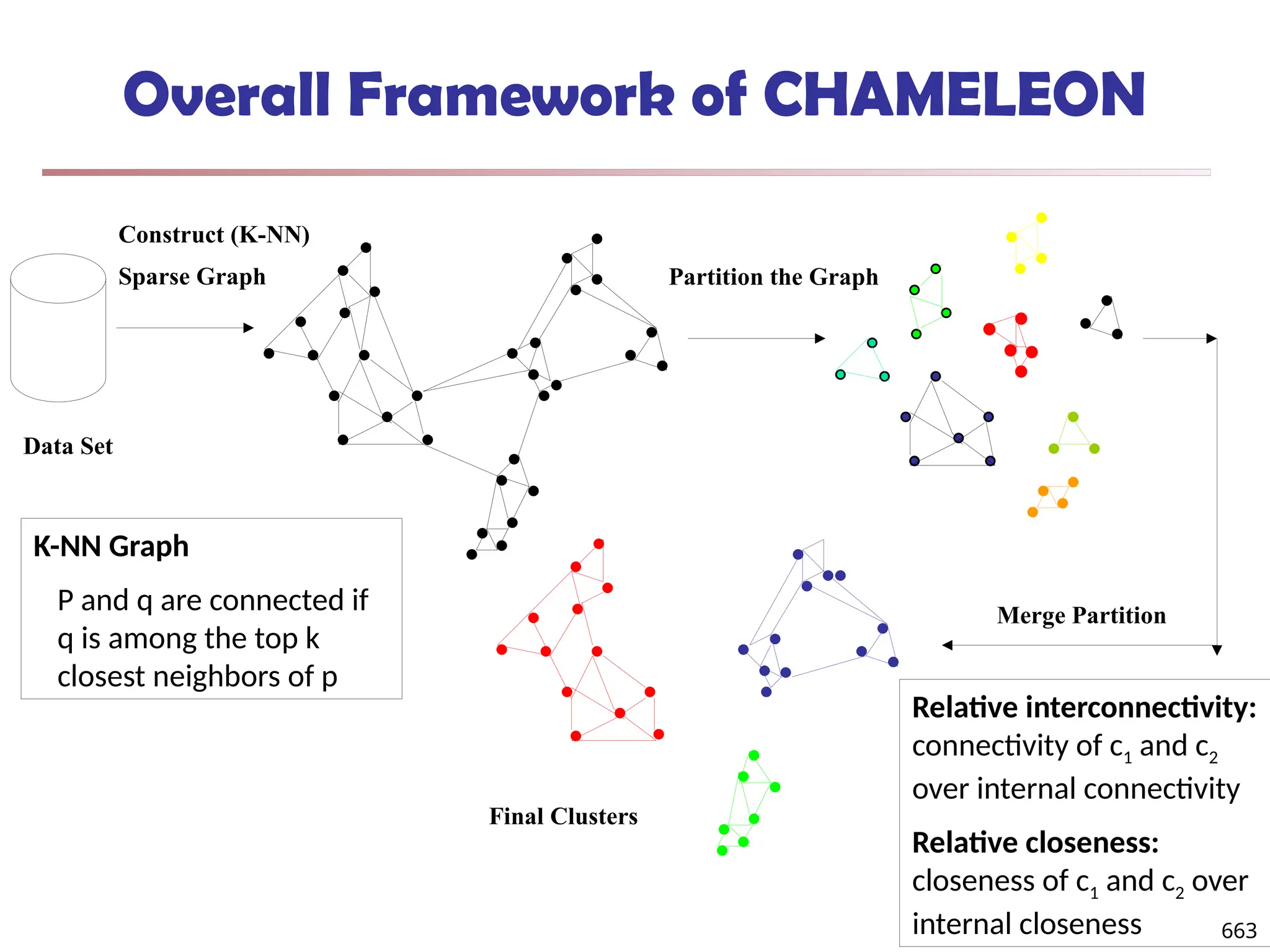













































![Observation 2: Distribution of Similarity
Power law distribution exists in similarities
56% of similarity entries are in [0.005, 0.015]
1.4% of similarity entries are larger than 0.1
Can we design a data structure that stores the significant
similarities and compresses insignificant ones?
0
0.1
0.2
0.3
0.4
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0.2
0.22
0.24
similarity value
portion
of
entries
Distribution of SimRank similarities
among DBLP authors
719](https://image.slidesharecdn.com/dwdm3rdeditiontextbookslides-241024155956-ed696a42/75/DWDM-3rd-EDITION-TEXT-BOOK-SLIDES24-pptx-717-2048.jpg)
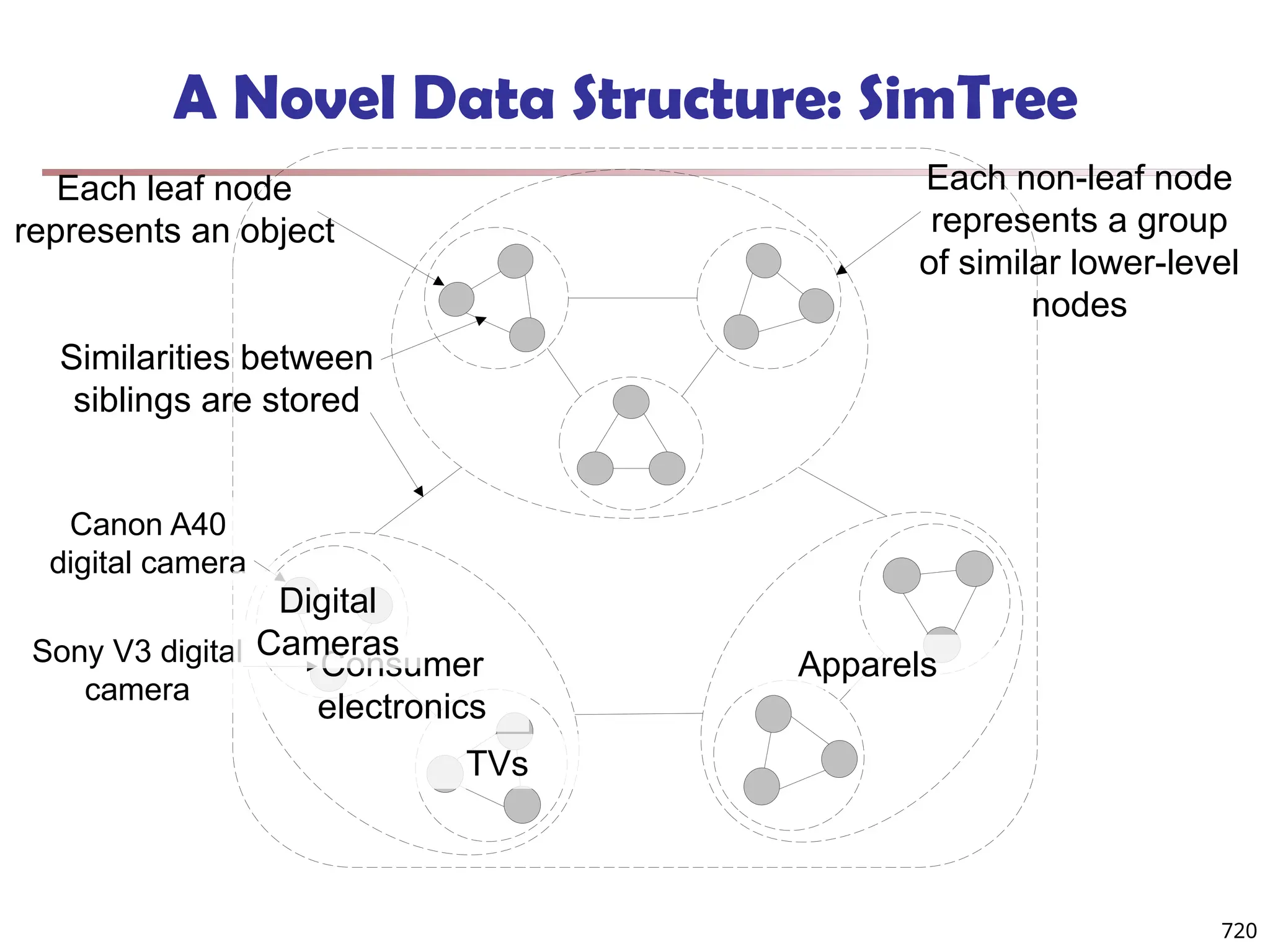




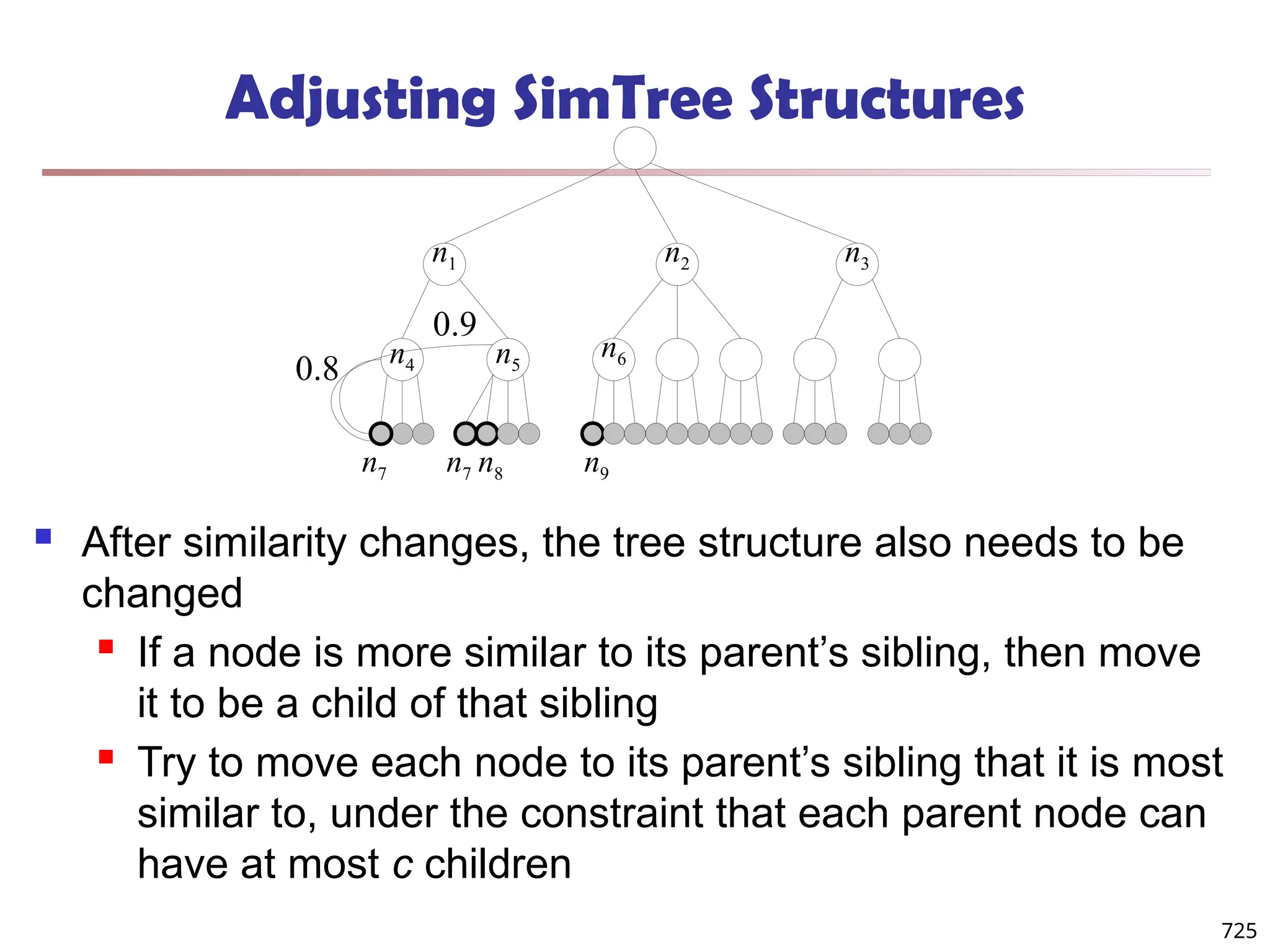
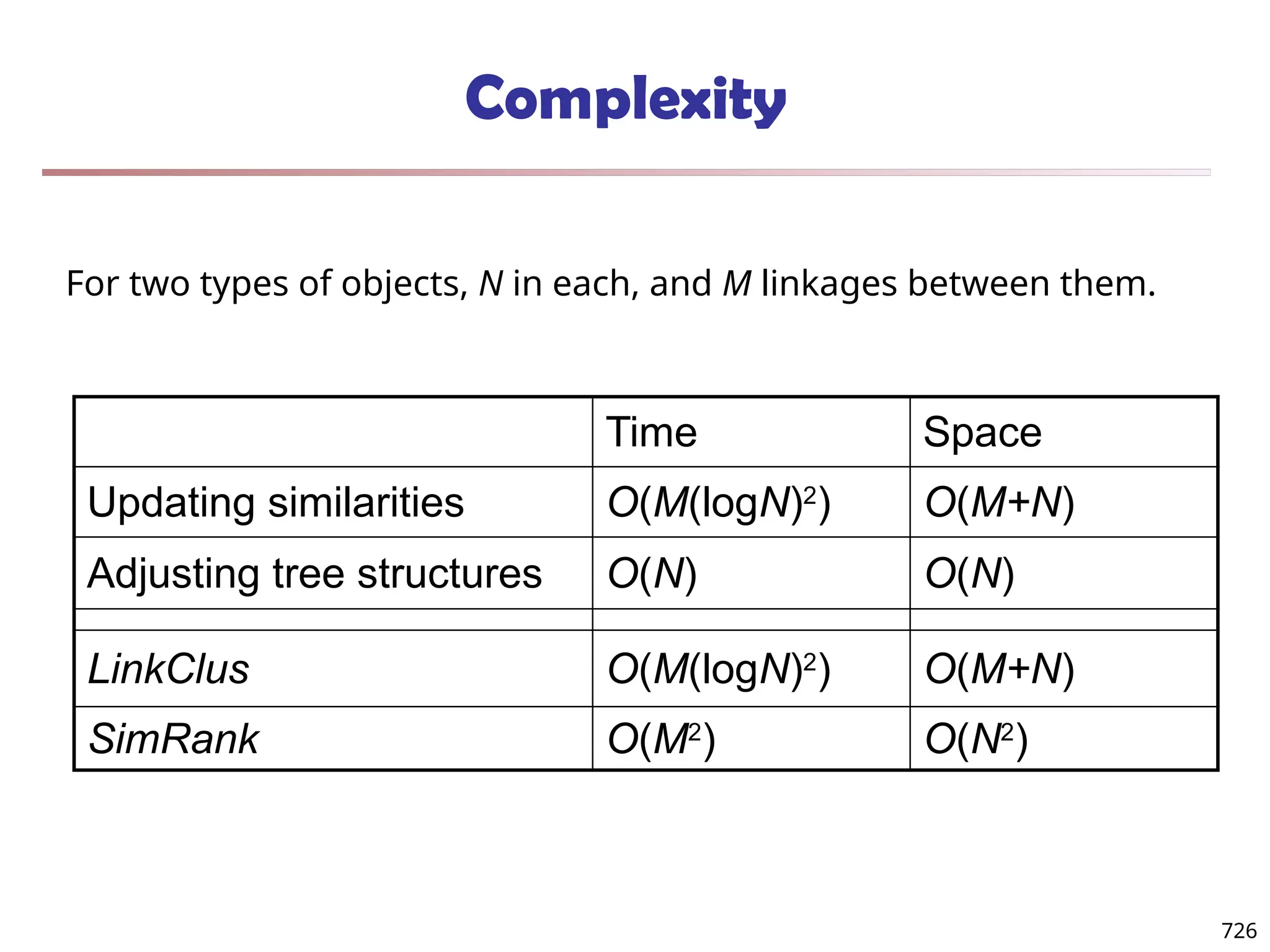



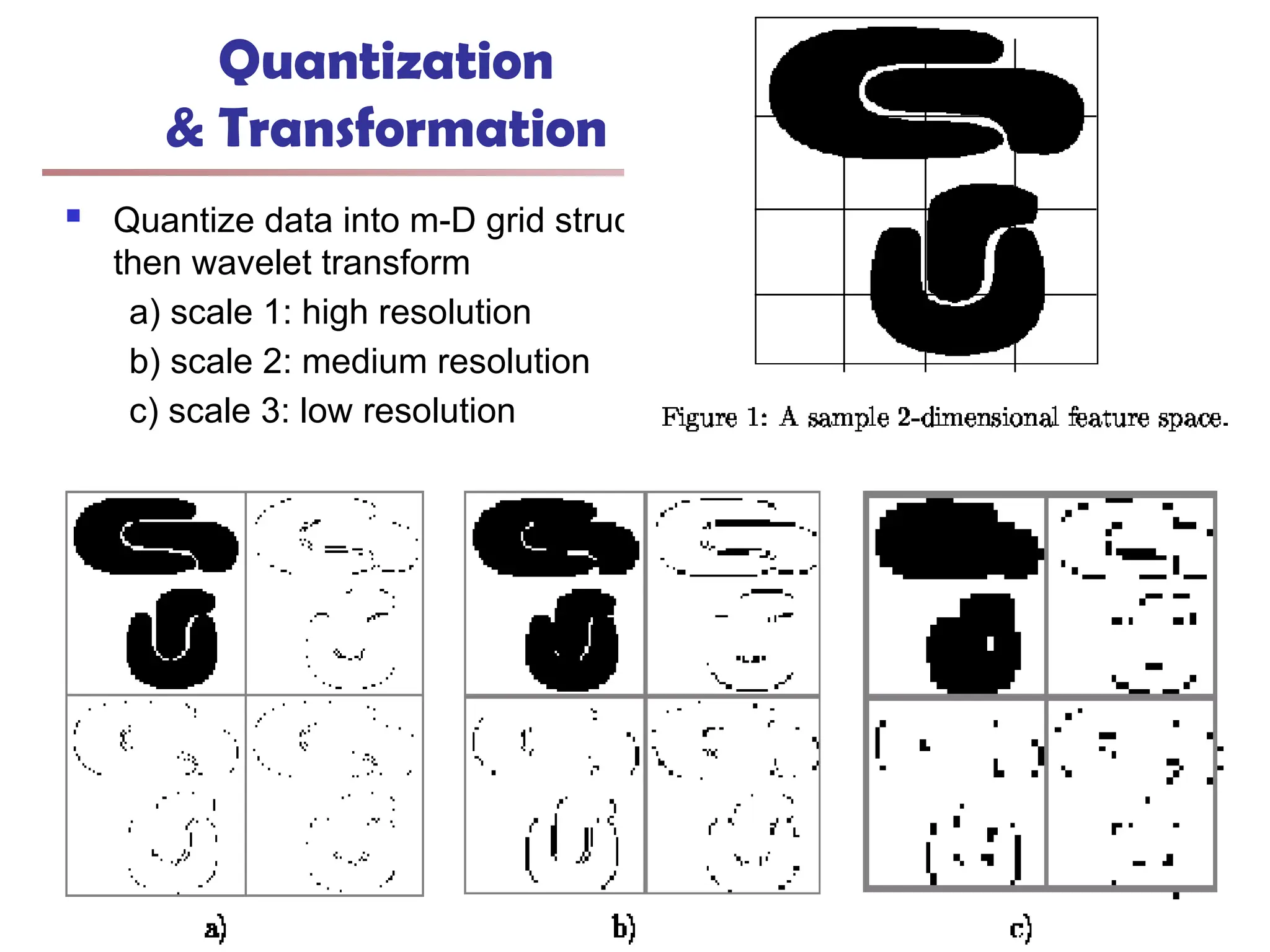


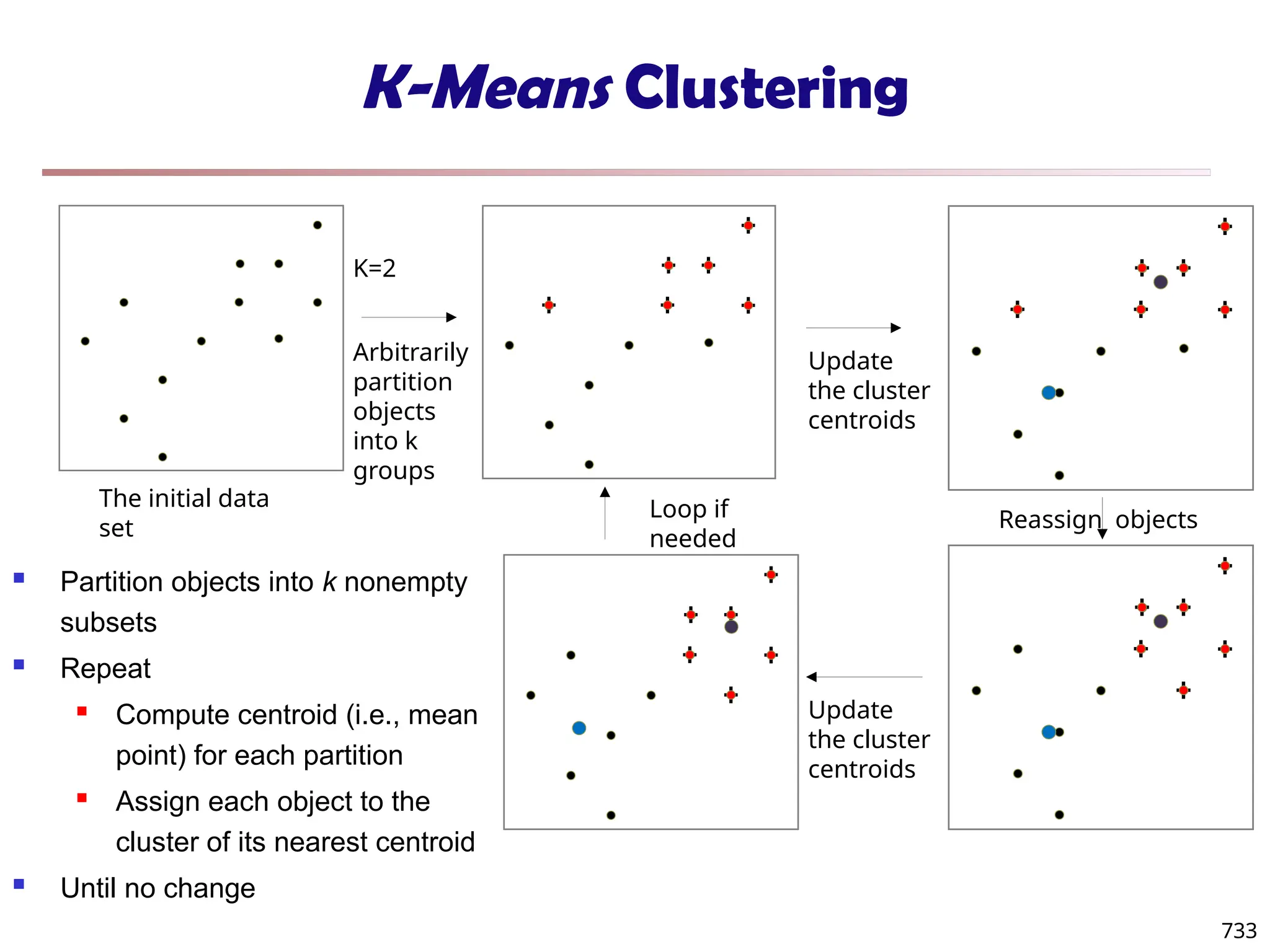
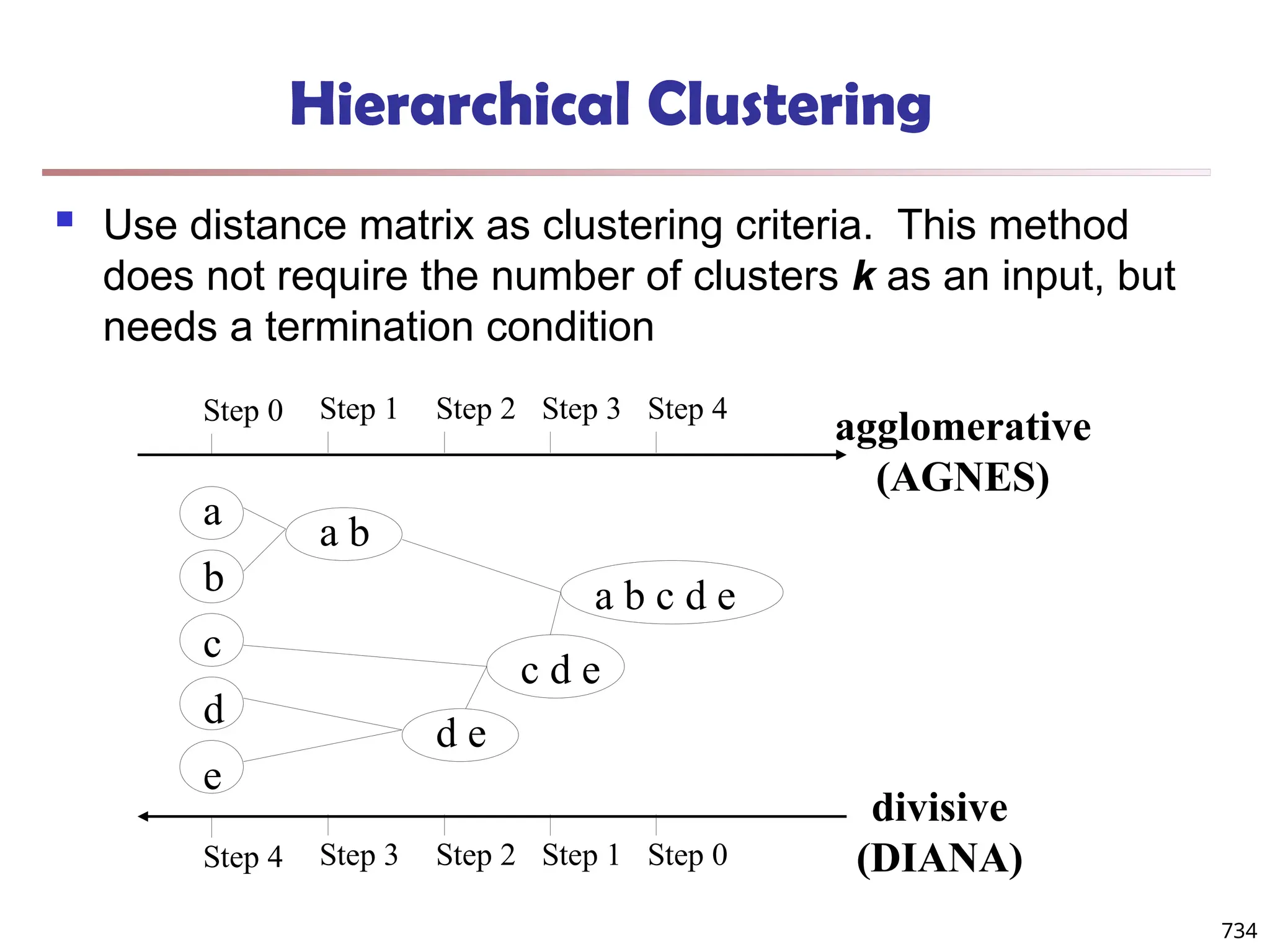

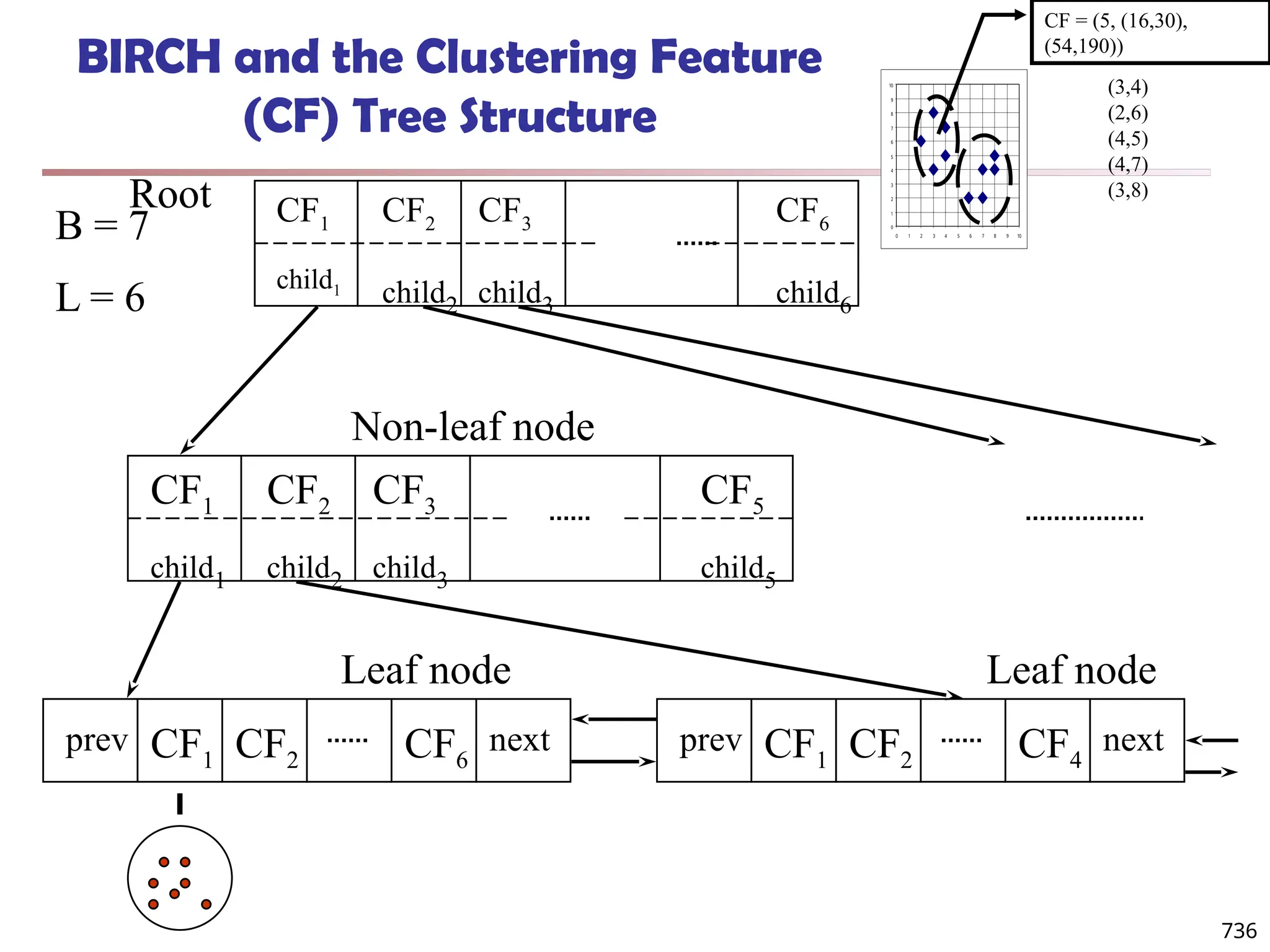
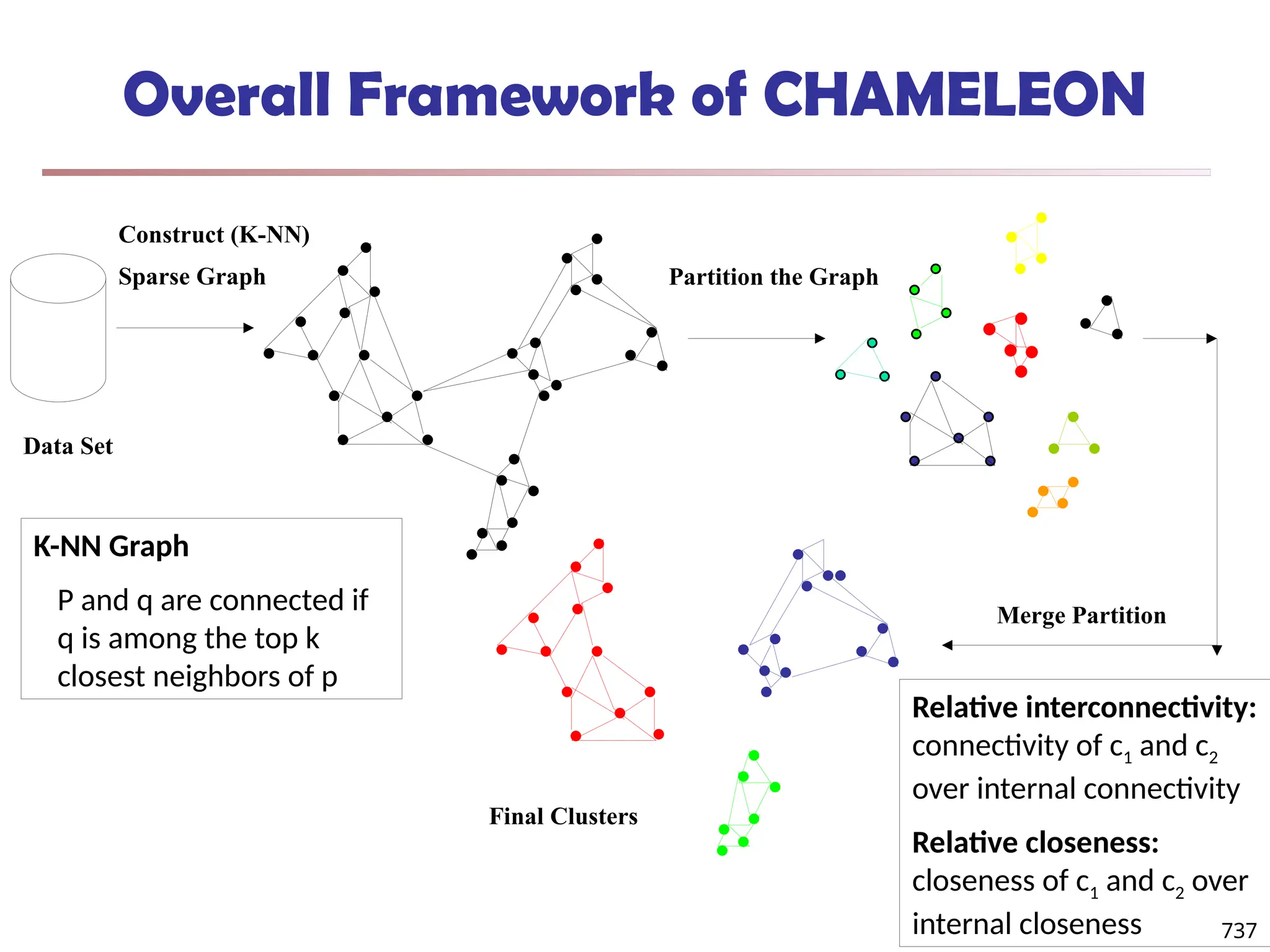

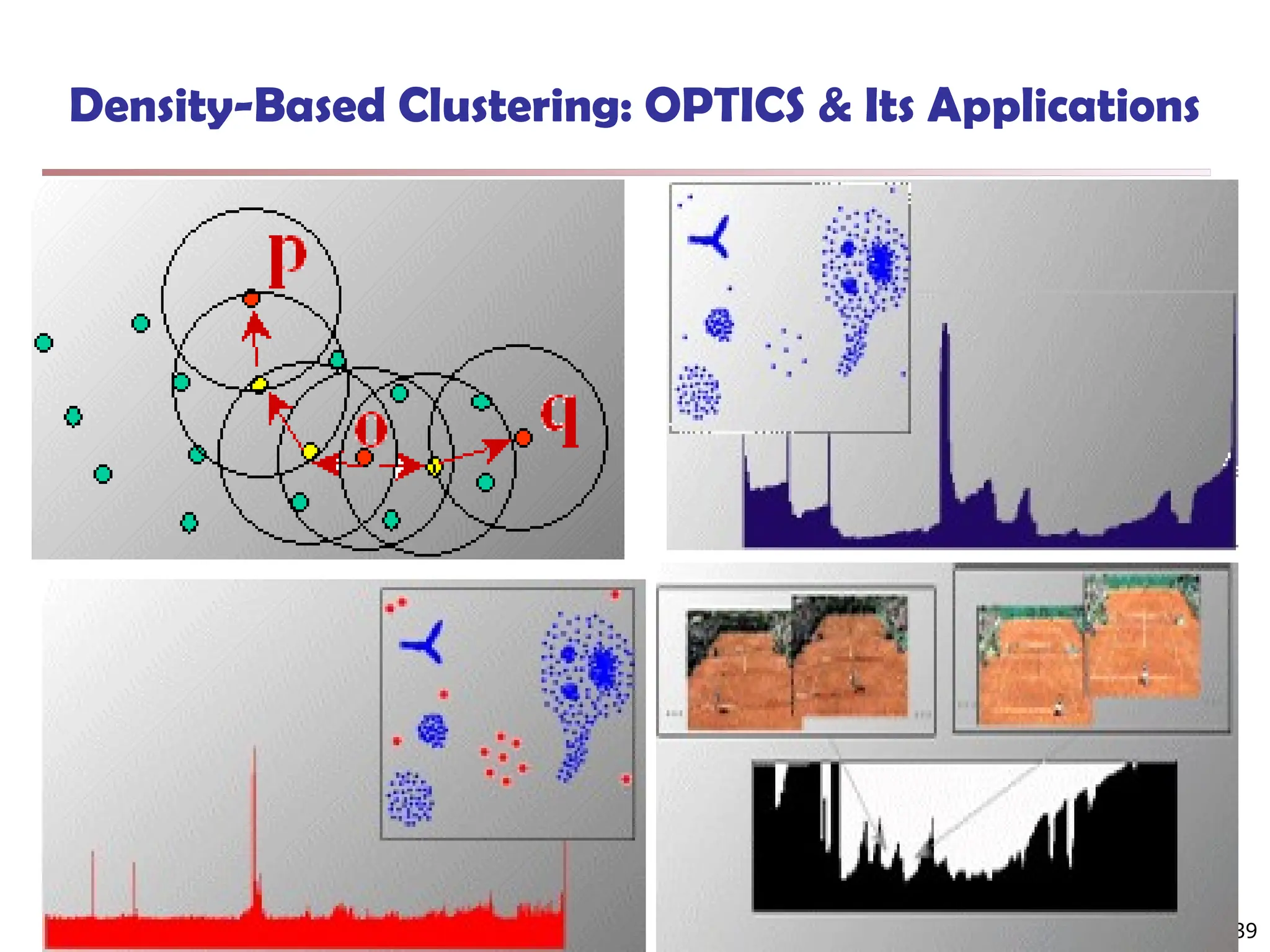
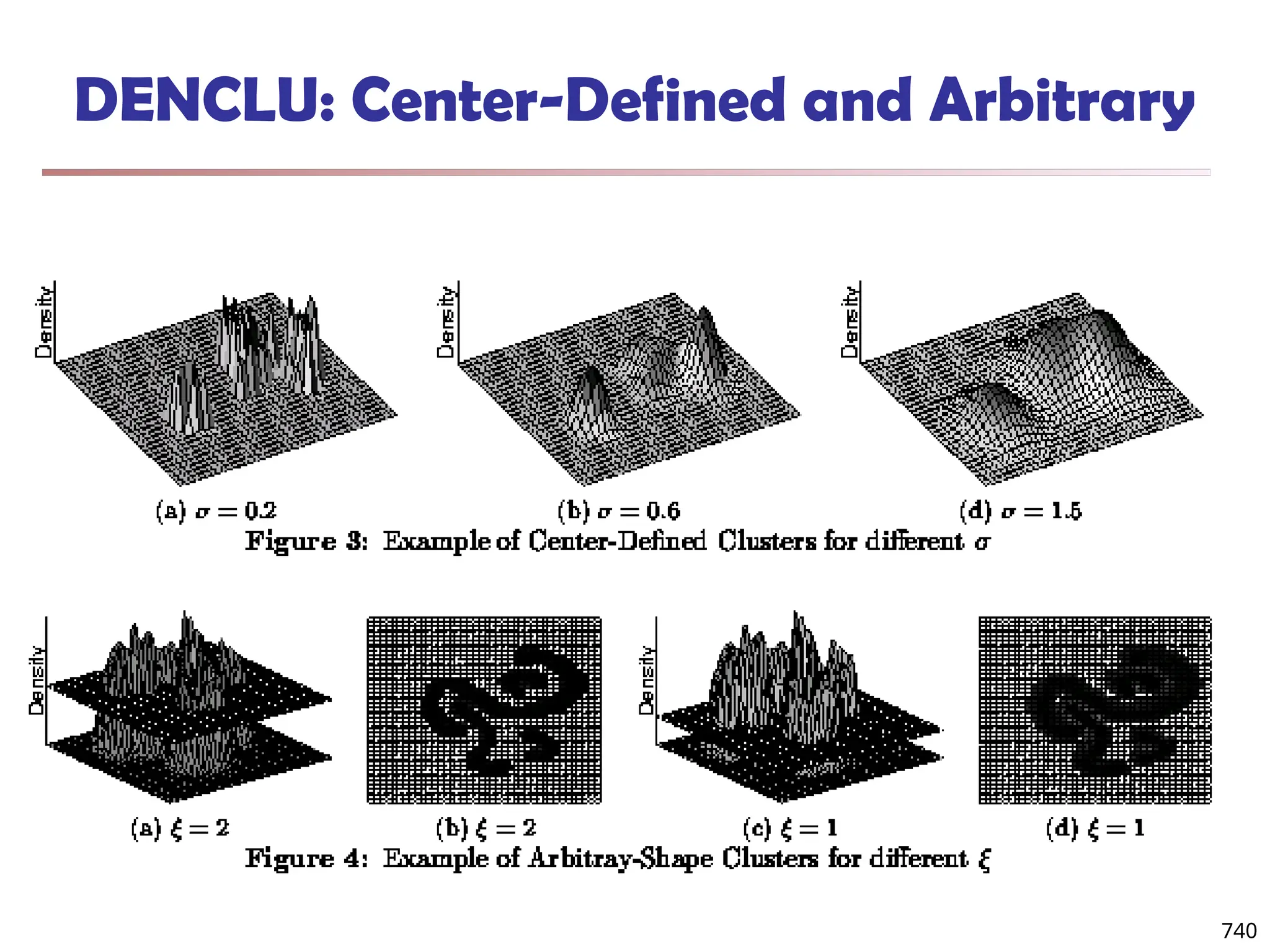
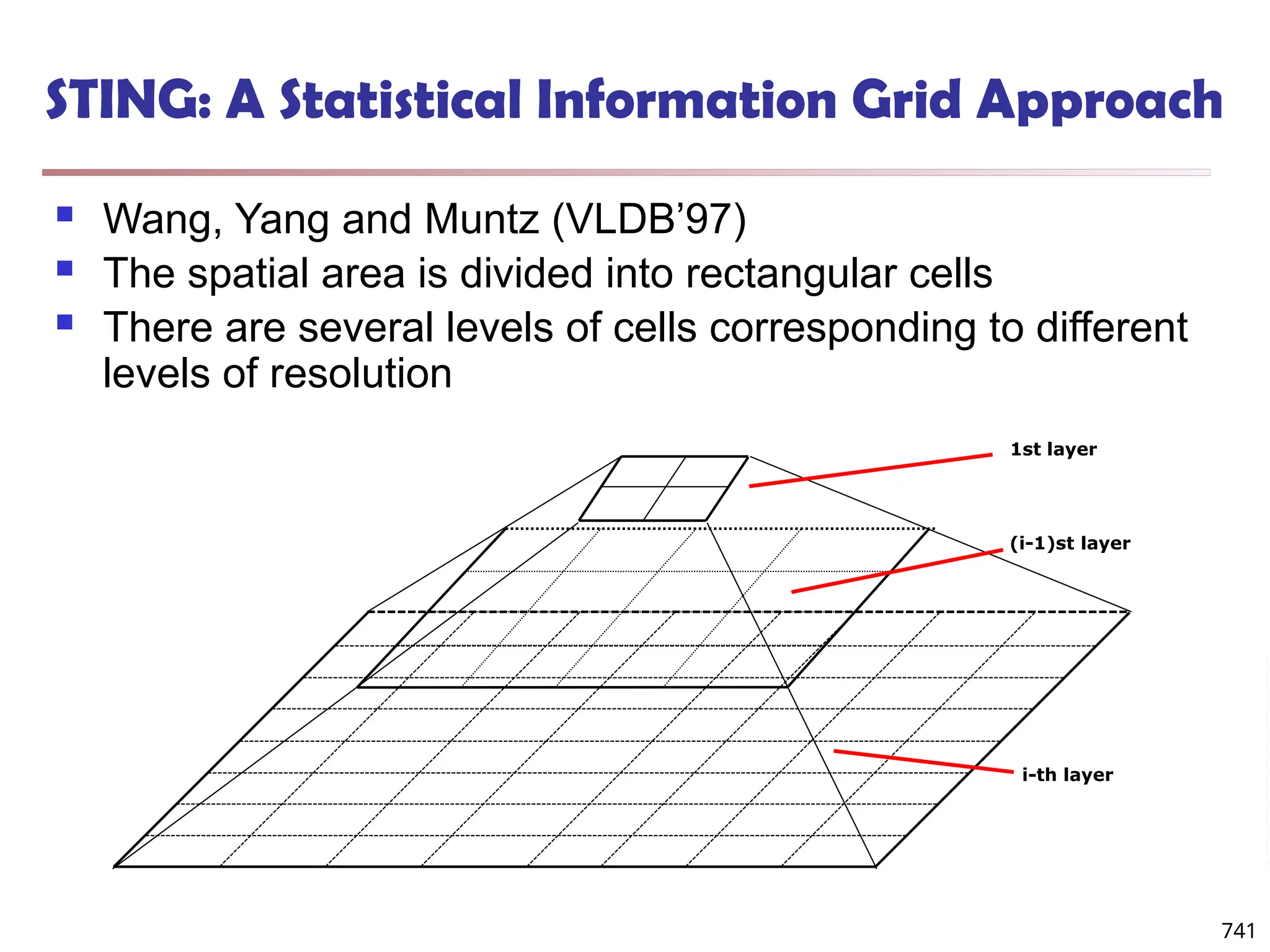



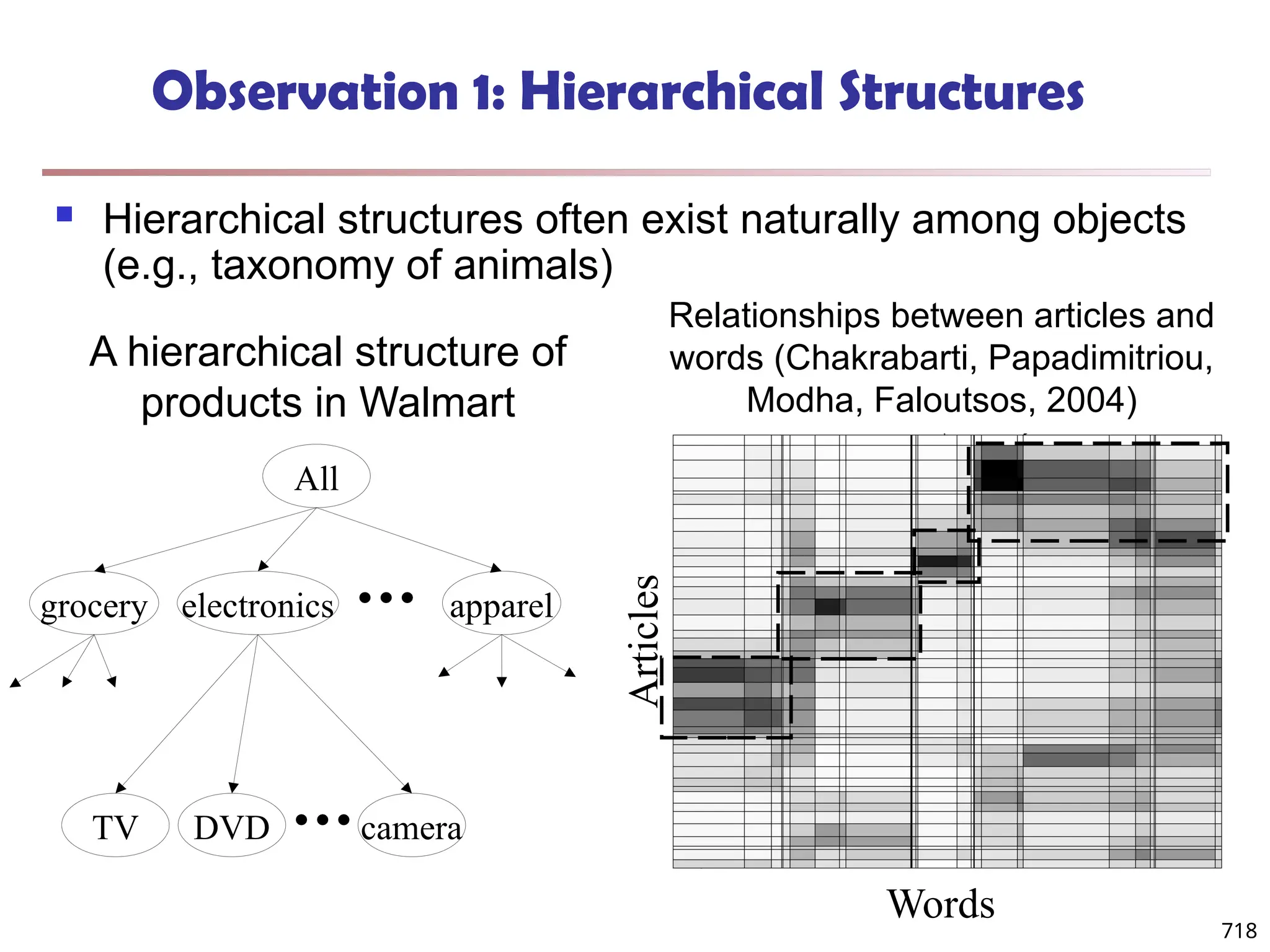
![Fuzzy Set and Fuzzy Cluster
Clustering methods discussed so far
Every data object is assigned to exactly one cluster
Some applications may need for fuzzy or soft cluster assignment
Ex. An e-game could belong to both entertainment and software
Methods: fuzzy clusters and probabilistic model-based clusters
Fuzzy cluster: A fuzzy set S: FS : X → [0, 1] (value between 0 and 1)
Example: Popularity of cameras is defined as a fuzzy mapping
Then, A(0.05), B(1), C(0.86), D(0.27)
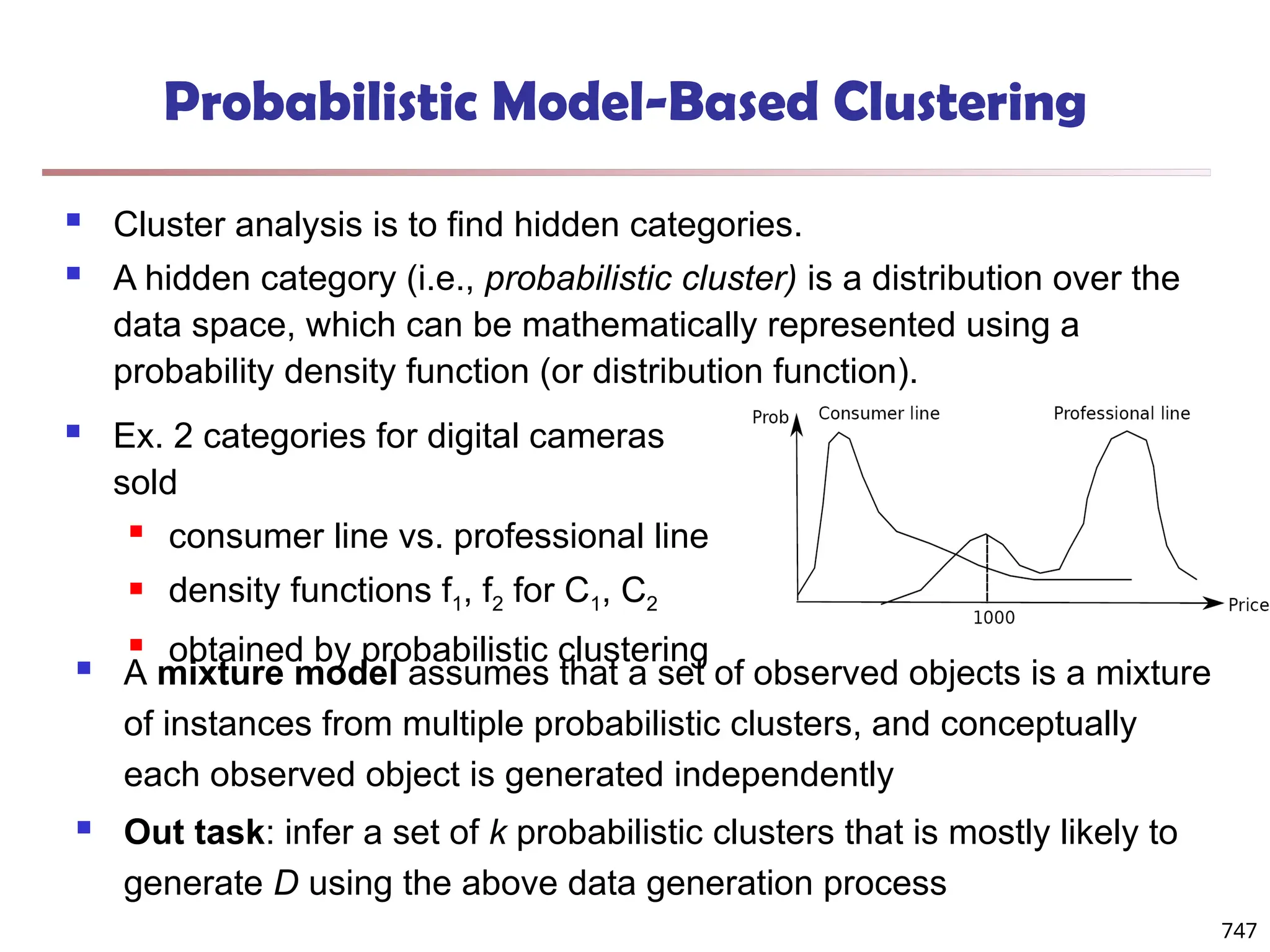
745](https://image.slidesharecdn.com/dwdm3rdeditiontextbookslides-241024155956-ed696a42/75/DWDM-3rd-EDITION-TEXT-BOOK-SLIDES24-pptx-743-2048.jpg)
![Fuzzy (Soft) Clustering
Example: Let cluster features be
C1 :“digital camera” and “lens”
C2: “computer“
Fuzzy clustering
k fuzzy clusters C1, …,Ck ,represented as a partition matrix M = [wij]
P1: for each object oi and cluster Cj, 0 ≤ wij ≤ 1 (fuzzy set)
P2: for each object oi, , equal participation in the clustering
P3: for each cluster Cj , ensures there is no empty cluster
Let c1, …, ck as the center of the k clusters
For an object oi, sum of the squared error (SSE), p is a parameter:
For a cluster Ci, SSE:
Measure how well a clustering fits the data:
746](https://image.slidesharecdn.com/dwdm3rdeditiontextbookslides-241024155956-ed696a42/75/DWDM-3rd-EDITION-TEXT-BOOK-SLIDES24-pptx-744-2048.jpg)

















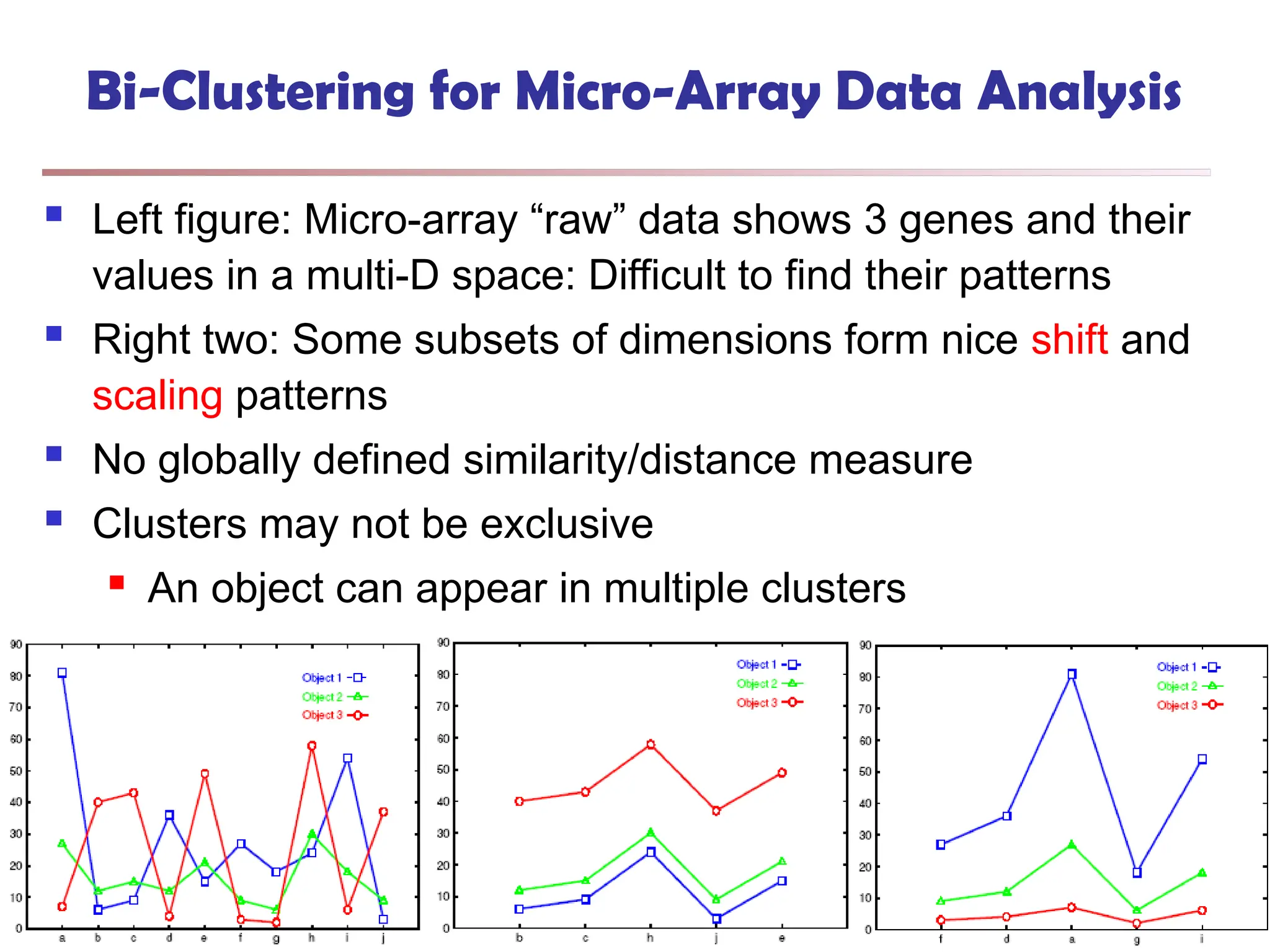


![Bi-Clustering (II): δ-pCluster
Enumerating all bi-clusters (δ-pClusters) [H. Wang, et al., Clustering by pattern
similarity in large data sets. SIGMOD’02]
Since a submatrix I x J is a bi-cluster with (perfect) coherent values iff ei1j1 − ei2j1
= ei1j2 − ei2j2. For any 2 x 2 submatrix of I x J, define p-score
A submatrix I x J is a δ-pCluster (pattern-based cluster) if the p-score of every 2
x 2 submatrix of I x J is at most δ, where δ ≥ 0 is a threshold specifying a user's
tolerance of noise against a perfect bi-cluster
The p-score controls the noise on every element in a bi-cluster, while the mean
squared residue captures the average noise
Monotonicity: If I x J is a δ-pClusters, every x x y (x,y ≥ 2) submatrix of I x J is
also a δ-pClusters.
A δ-pCluster is maximal if no more row or column can be added into the cluster
and retain δ-pCluster: We only need to compute all maximal δ-pClusters.
770](https://image.slidesharecdn.com/dwdm3rdeditiontextbookslides-241024155956-ed696a42/75/DWDM-3rd-EDITION-TEXT-BOOK-SLIDES24-pptx-768-2048.jpg)



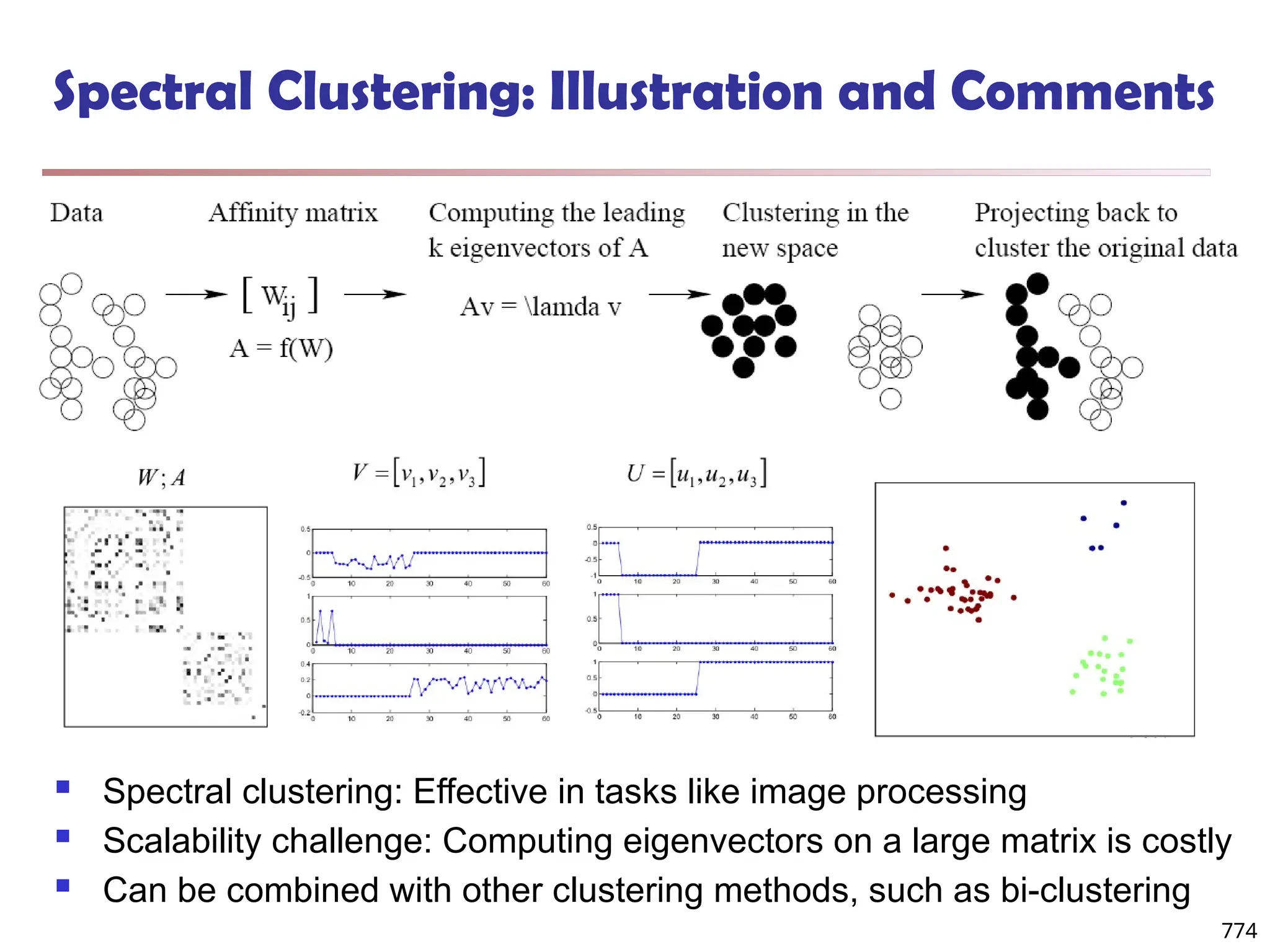



![SimRank: Similarity Based on Random
Walk and Structural Context
SimRank: structural-context similarity, i.e., based on the similarity of its
neighbors
In a directed graph G = (V,E),
individual in-neighborhood of v: I(v) = {u | (u, v) E}
∈
individual out-neighborhood of v: O(v) = {w | (v, w) E}
∈
Similarity in SimRank:
Initialization:
Then we can compute si+1 from si based on the definition
Similarity based on random walk: in a strongly connected component
Expected distance:
Expected meeting distance:
Expected meeting probability:
778
P[t] is the probability of the
tour](https://image.slidesharecdn.com/dwdm3rdeditiontextbookslides-241024155956-ed696a42/75/DWDM-3rd-EDITION-TEXT-BOOK-SLIDES24-pptx-776-2048.jpg)



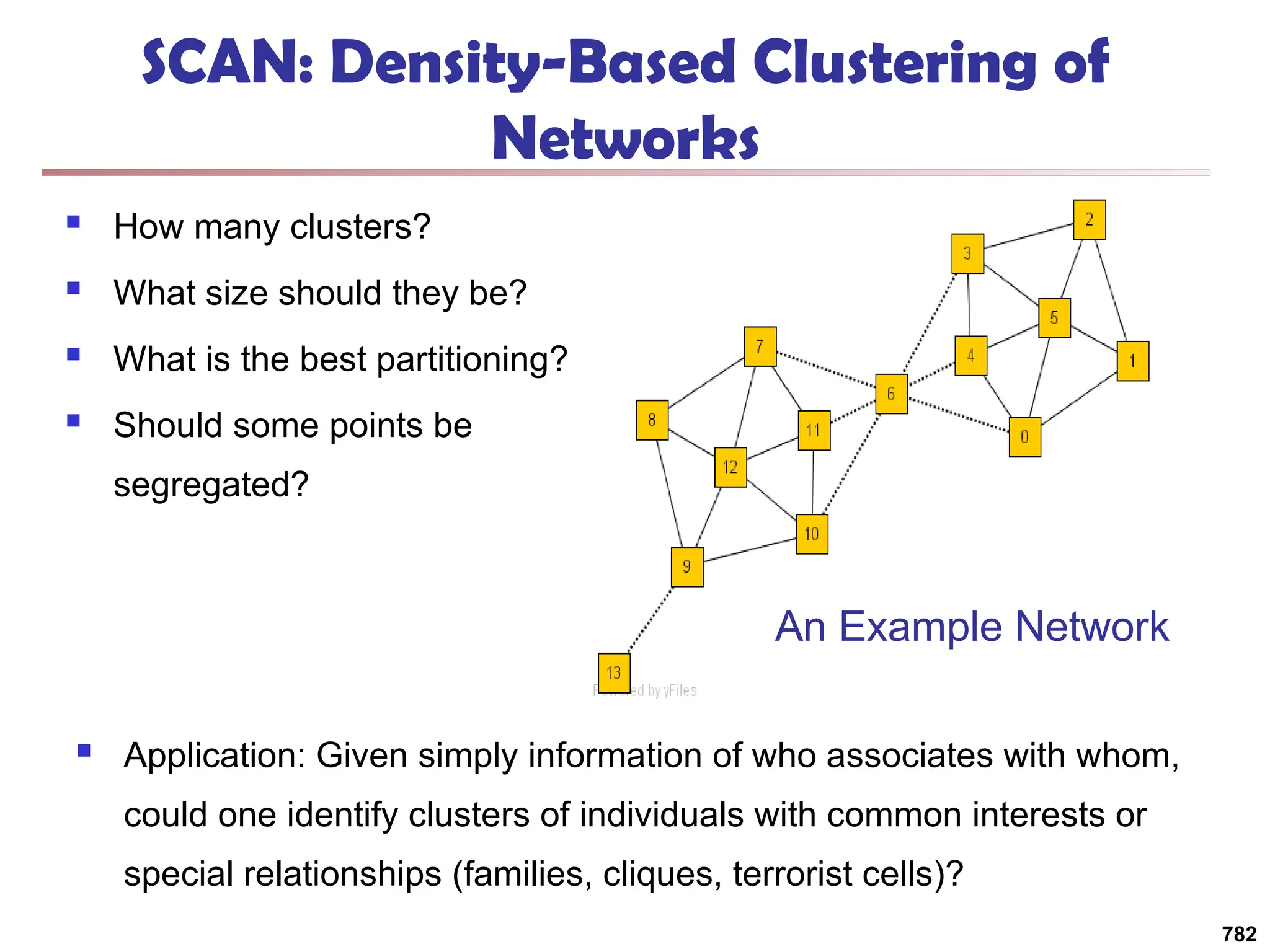
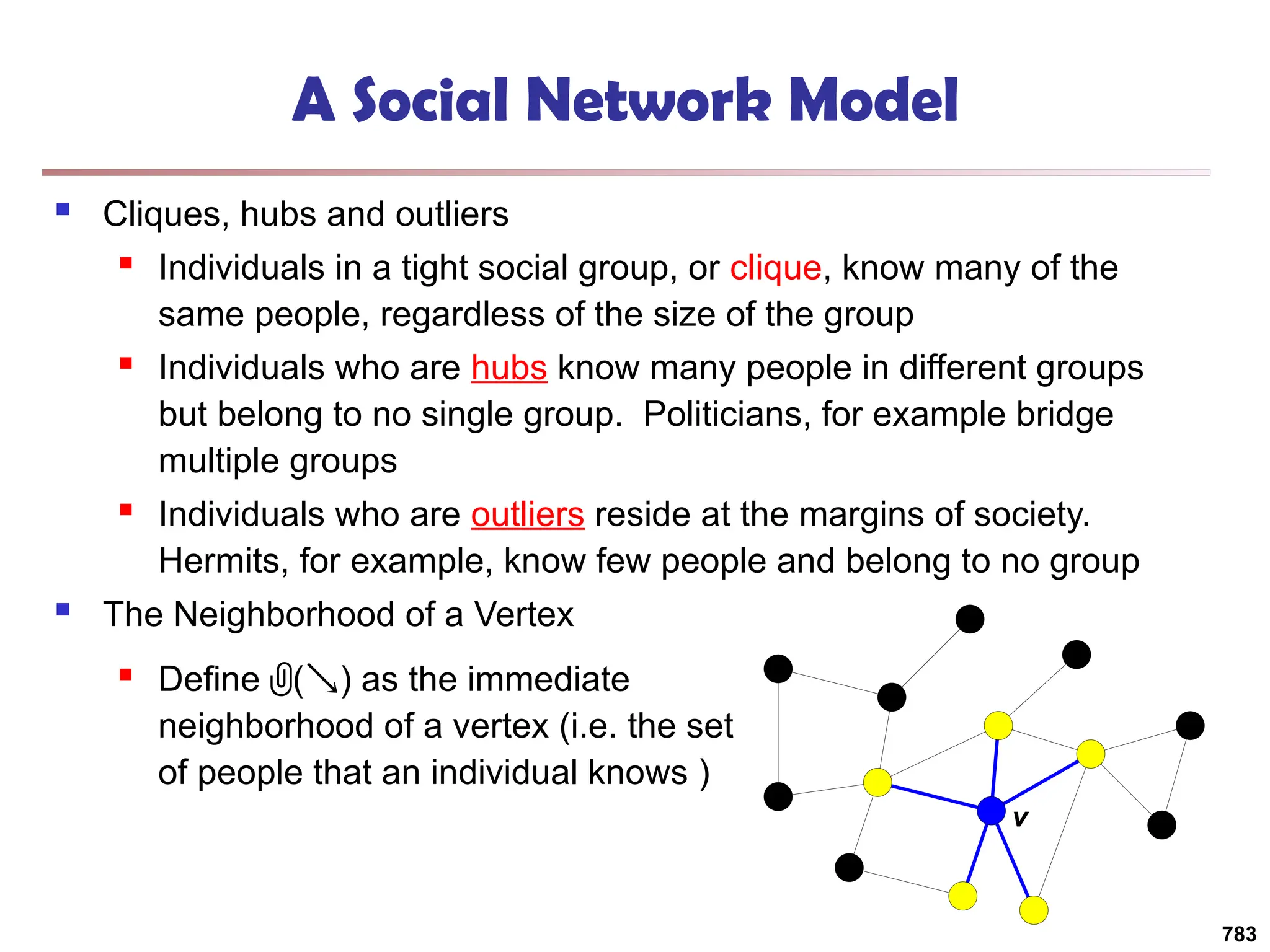
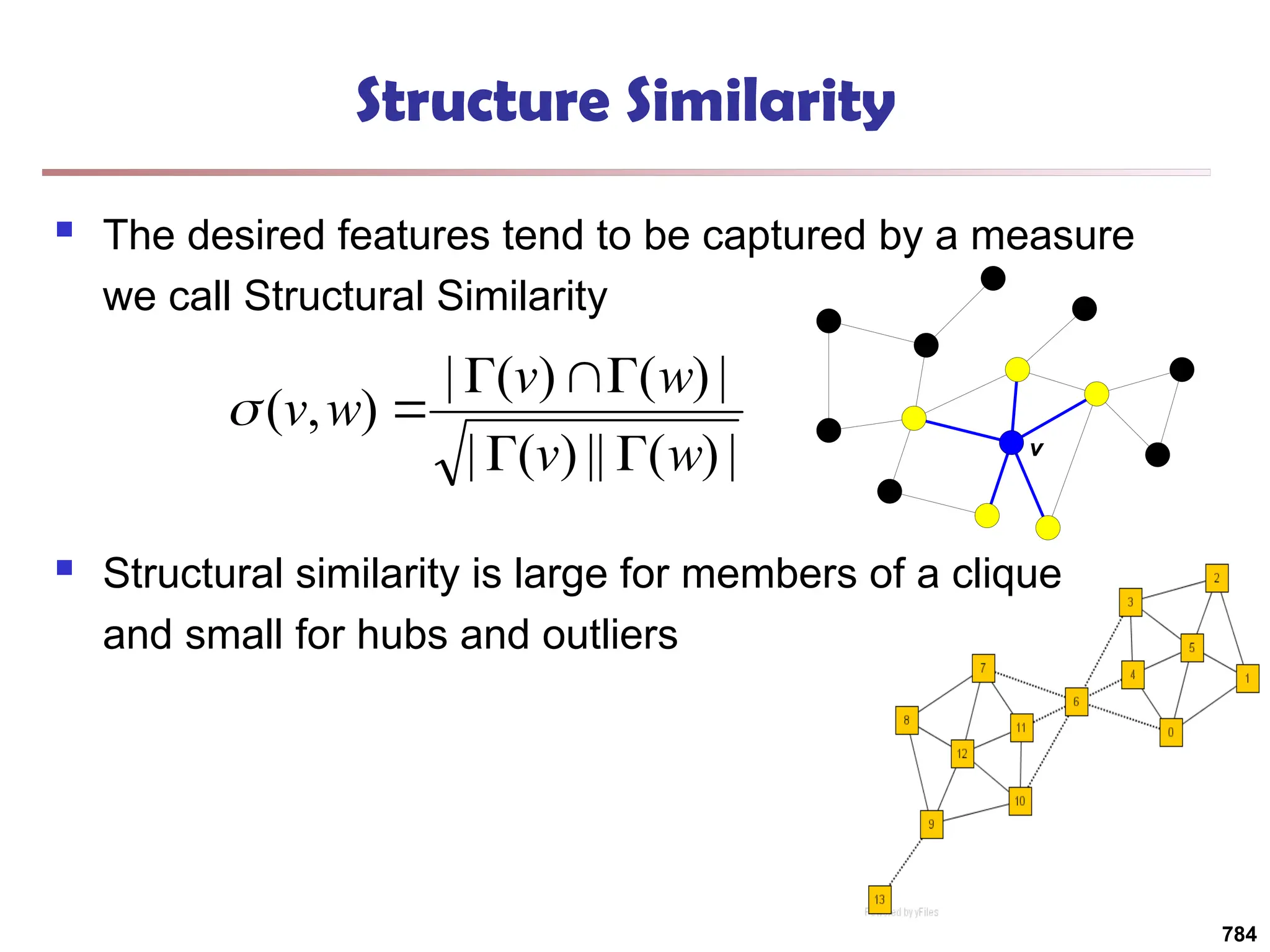
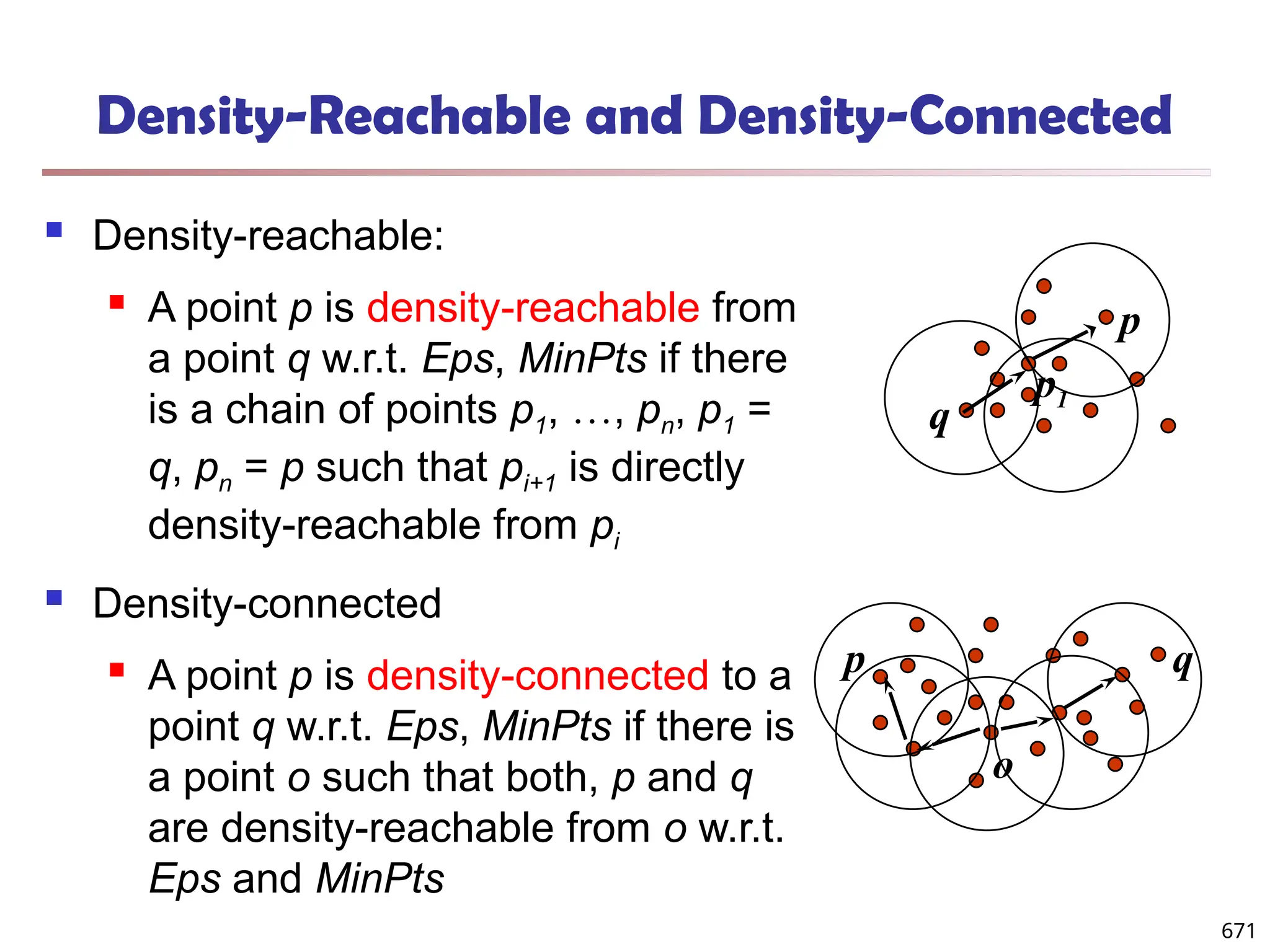
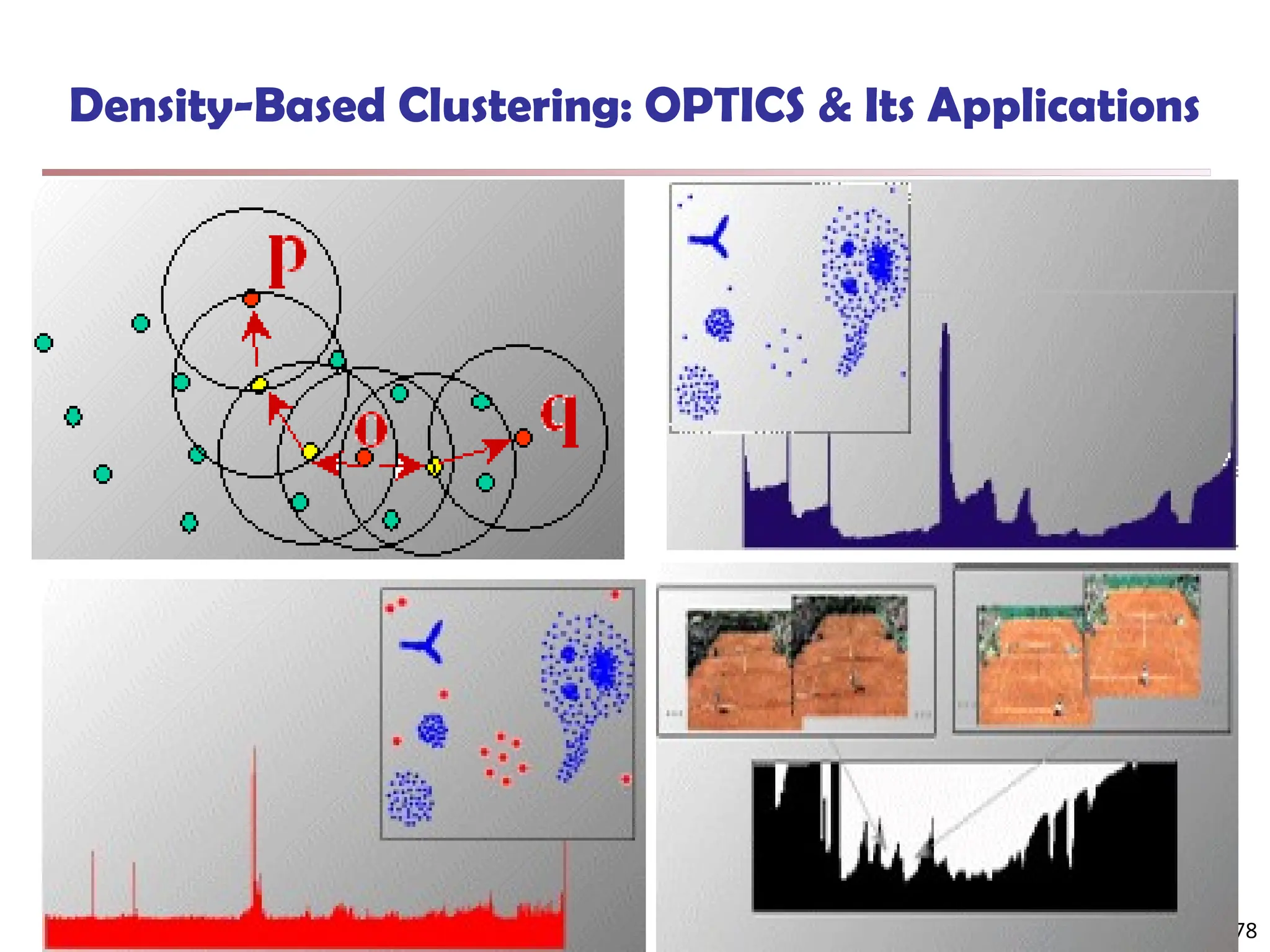
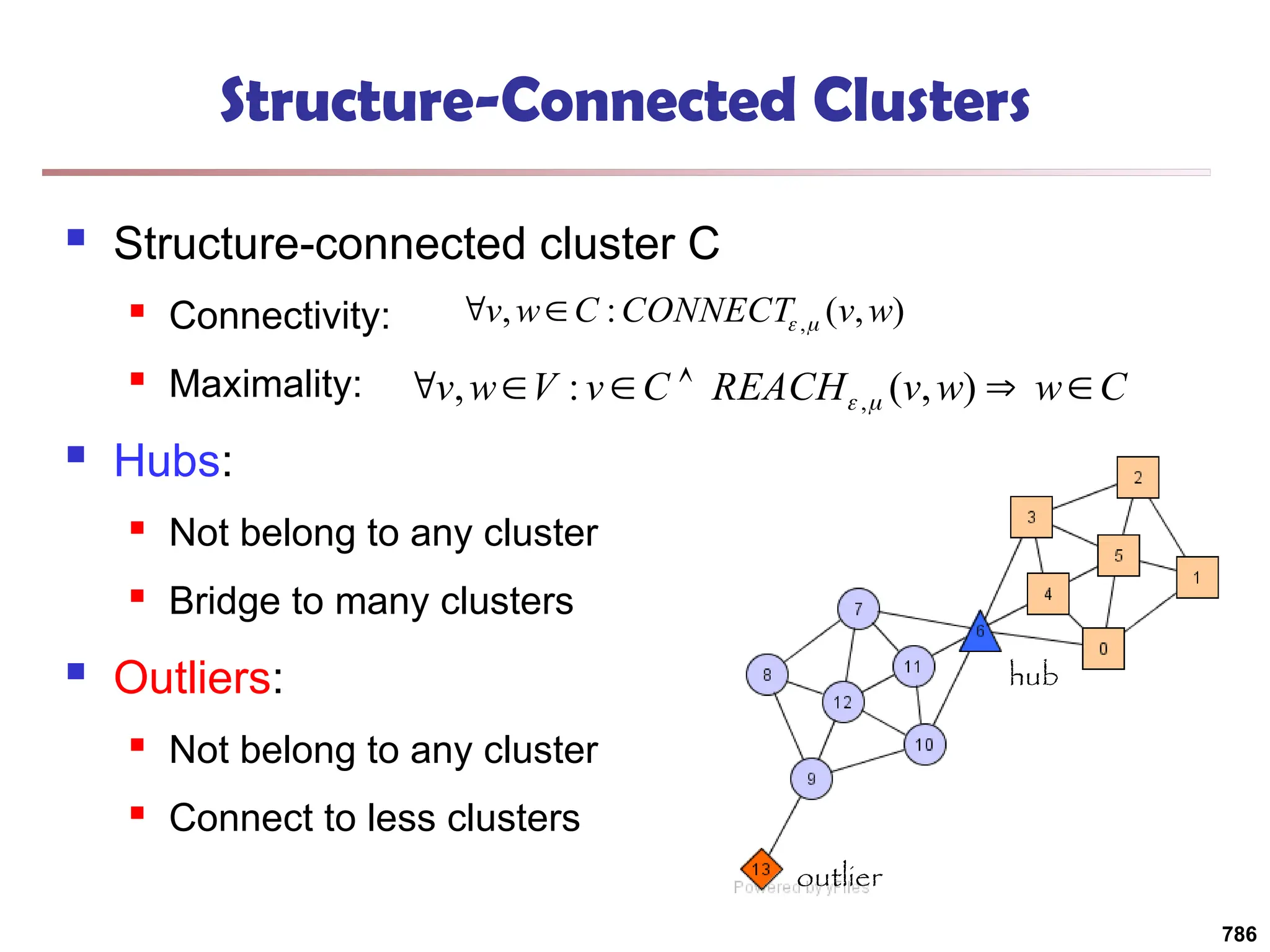
![Structural Connectivity [1]
-Neighborhood:
Core:
Direct structure reachable:
Structure reachable: transitive closure of direct structure
reachability
Structure connected:
}
)
,
(
|
)
(
{
)
(
w
v
v
w
v
N
|
)
(
|
)
(
, v
N
v
CORE
)
(
)
(
)
,
( ,
, v
N
w
v
CORE
w
v
DirRECH
)
,
(
)
,
(
:
)
,
( ,
,
, w
u
RECH
v
u
RECH
V
u
w
v
CONNECT
[1] M. Ester, H. P. Kriegel, J. Sander, & X. Xu (KDD'96) “A Density-Based
Algorithm for Discovering Clusters in Large Spatial Databases
785](https://image.slidesharecdn.com/dwdm3rdeditiontextbookslides-241024155956-ed696a42/75/DWDM-3rd-EDITION-TEXT-BOOK-SLIDES24-pptx-783-2048.jpg)

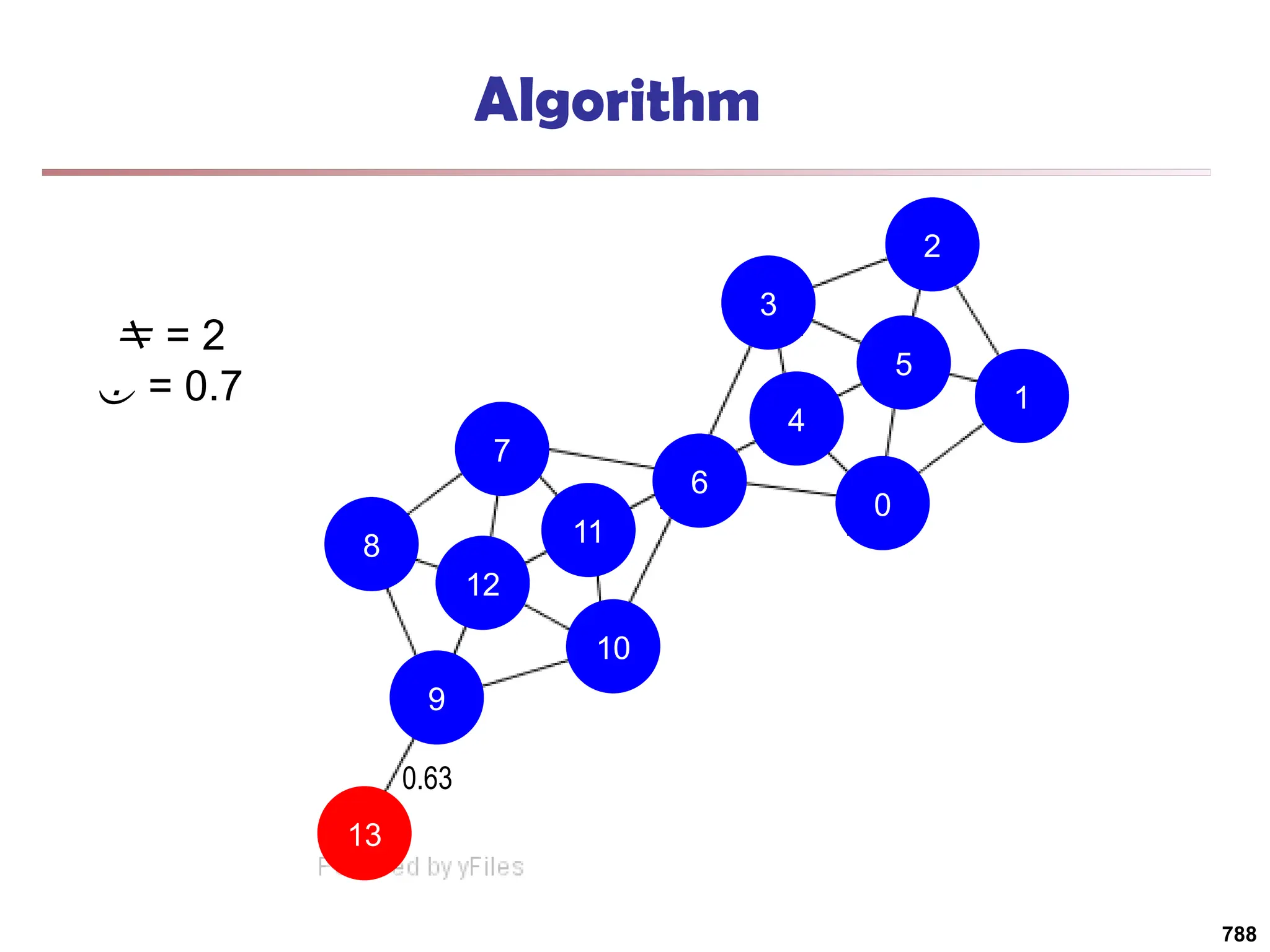

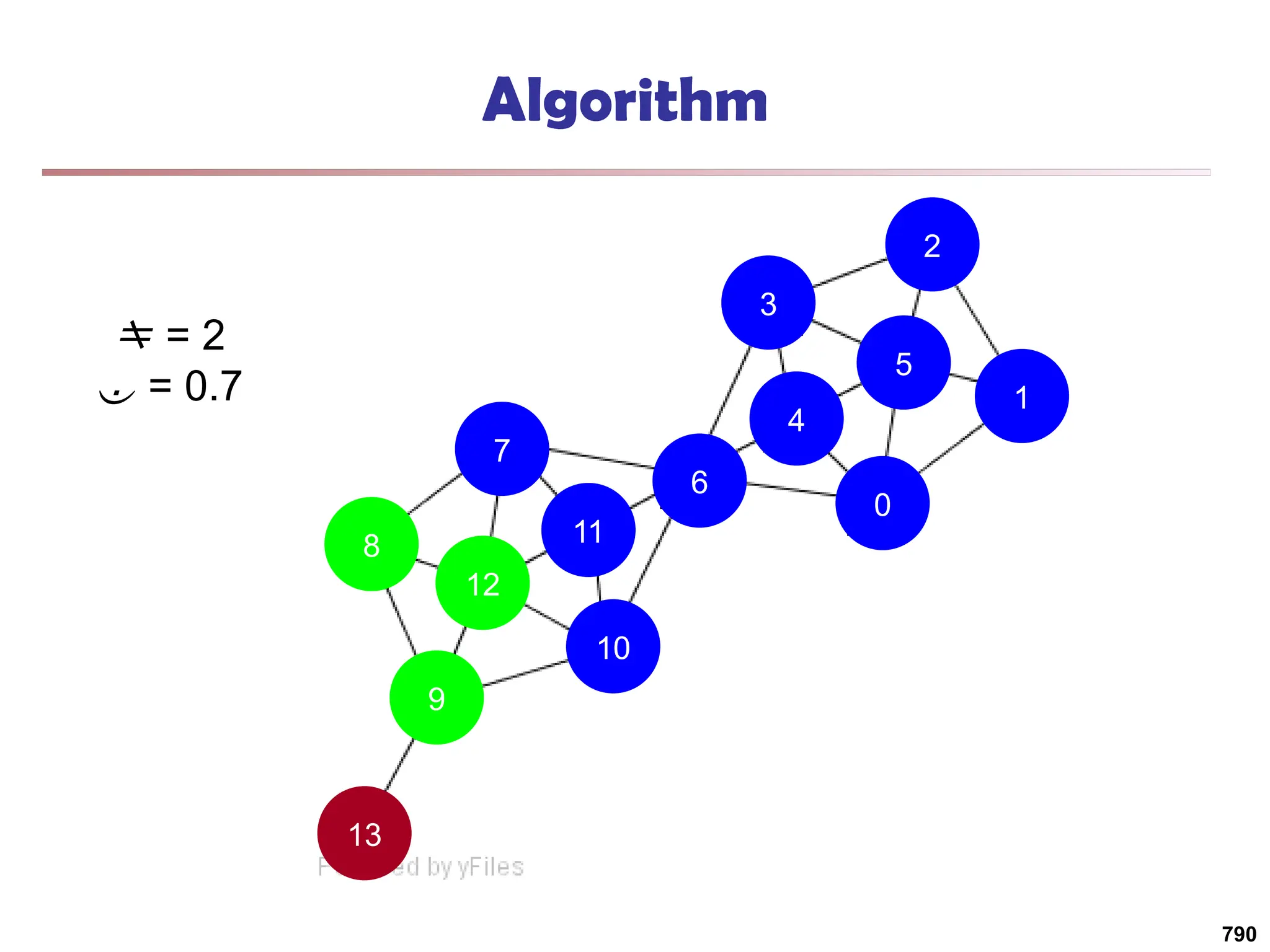
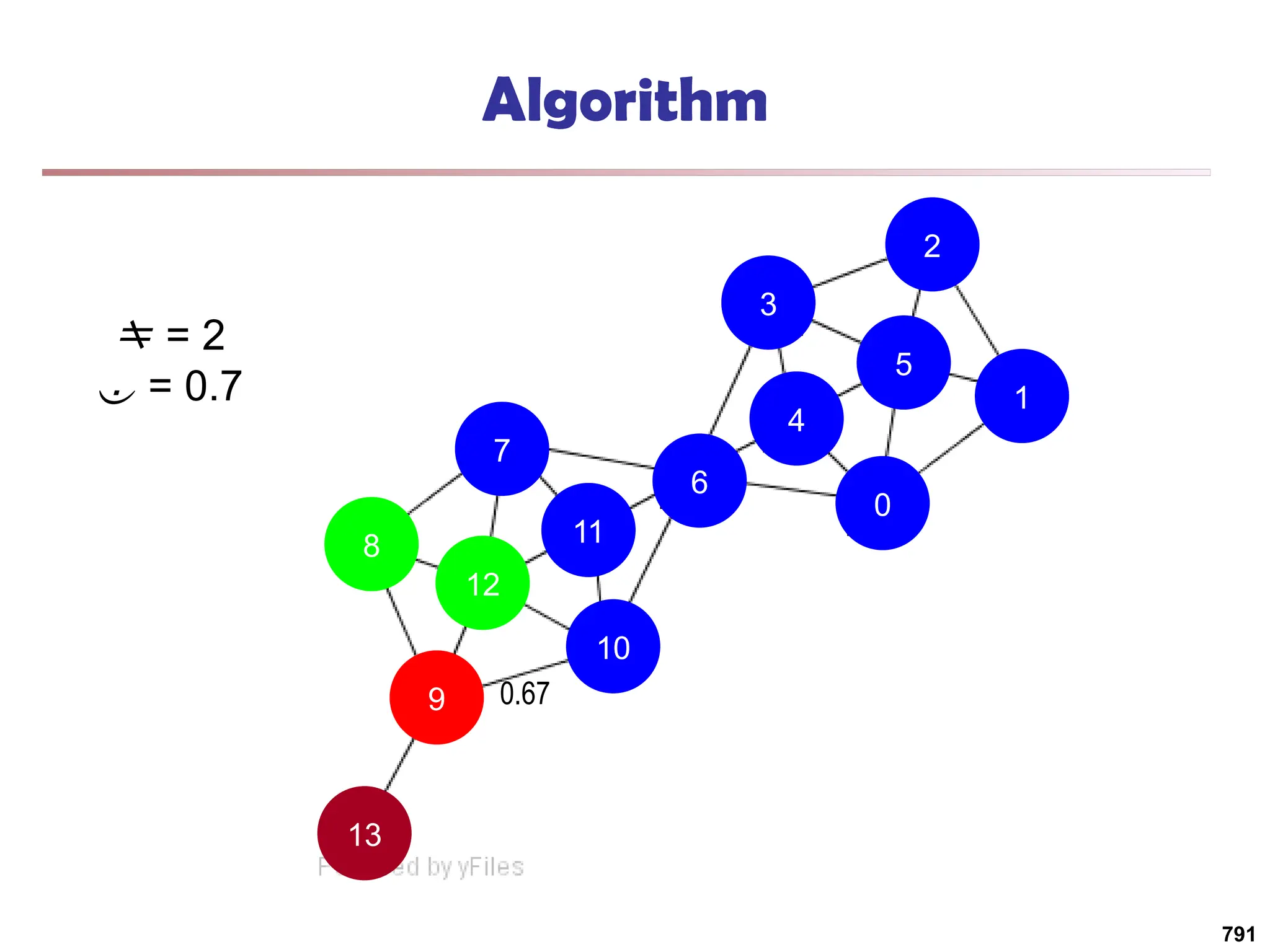
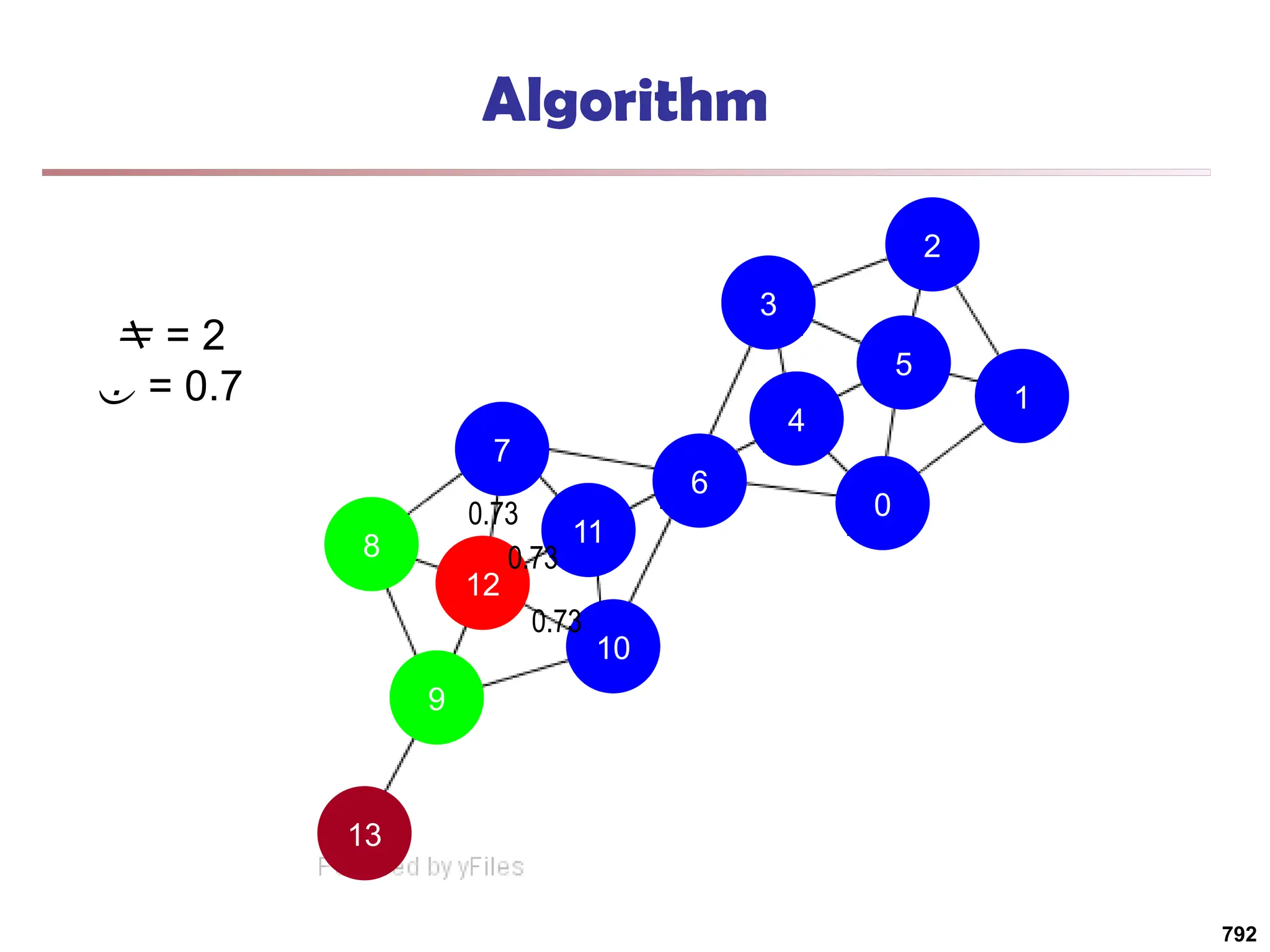
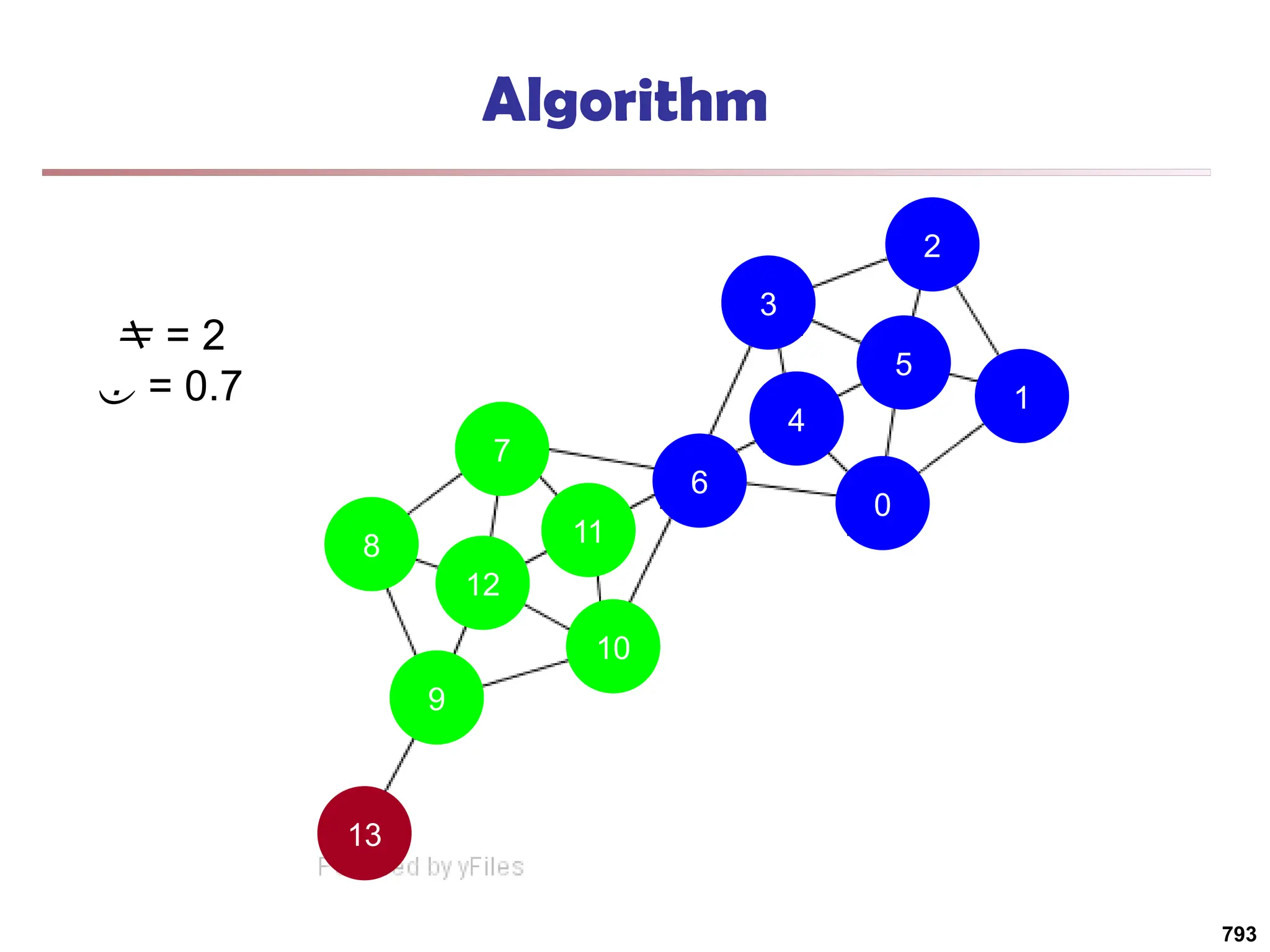

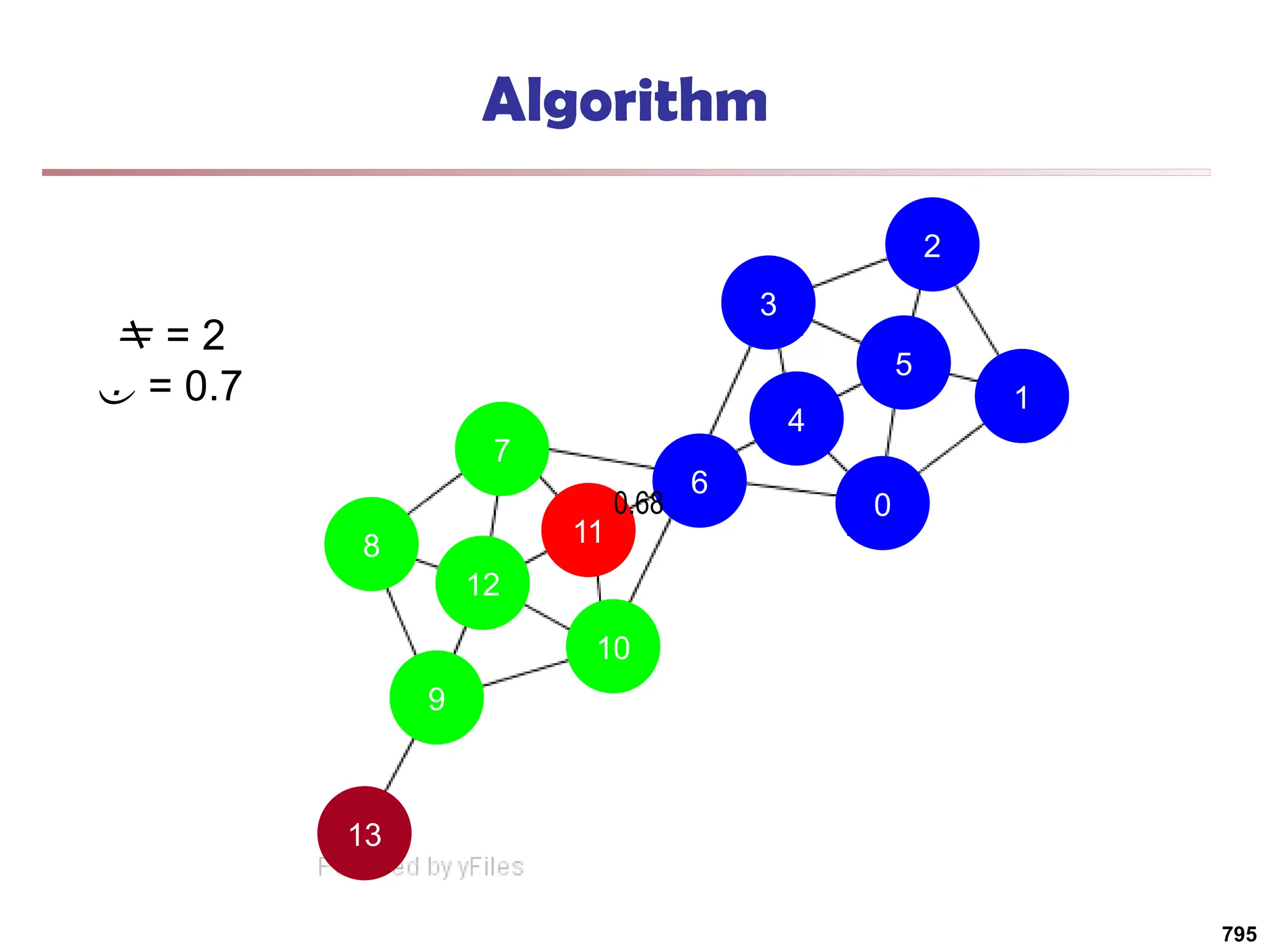
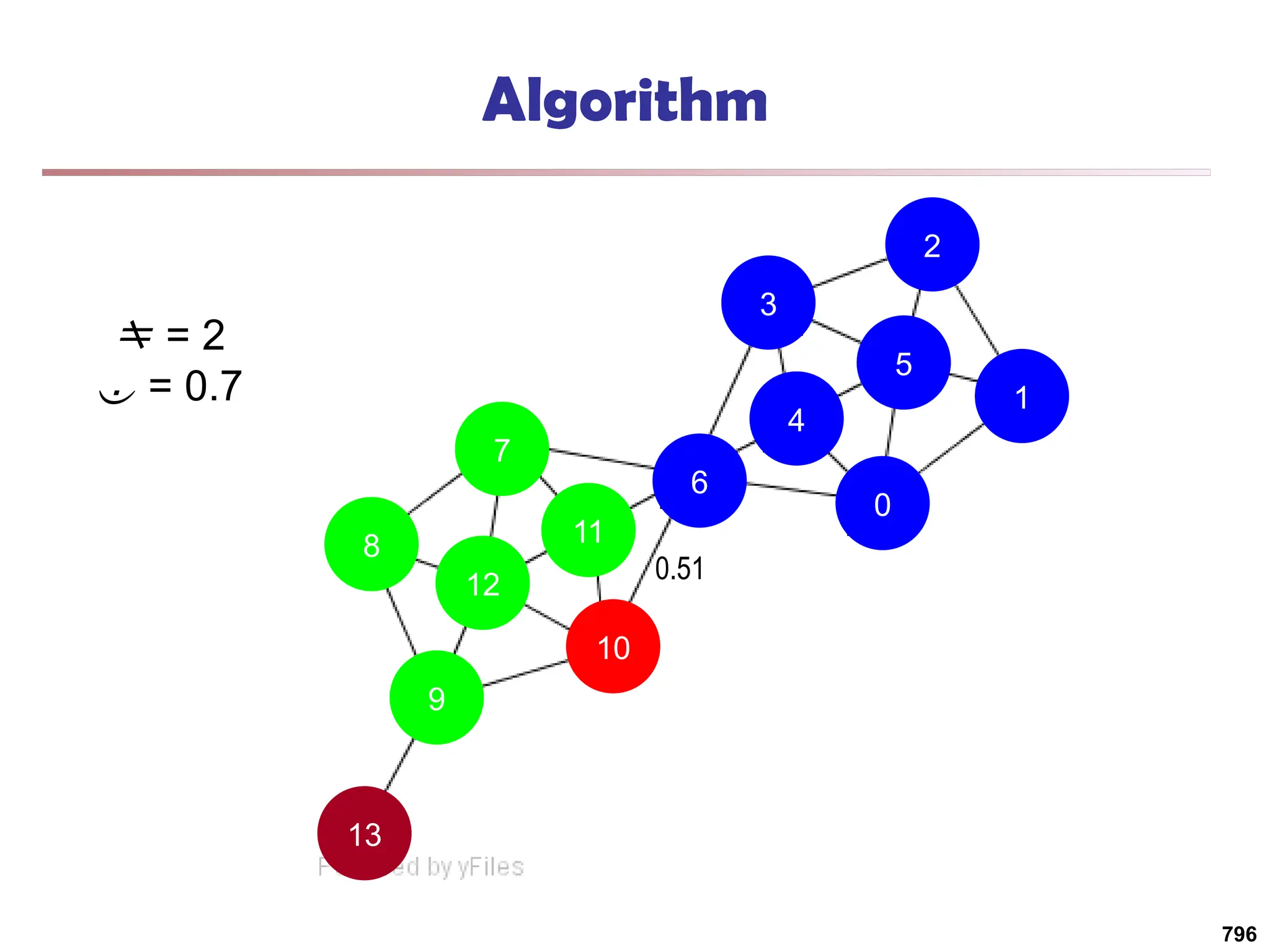
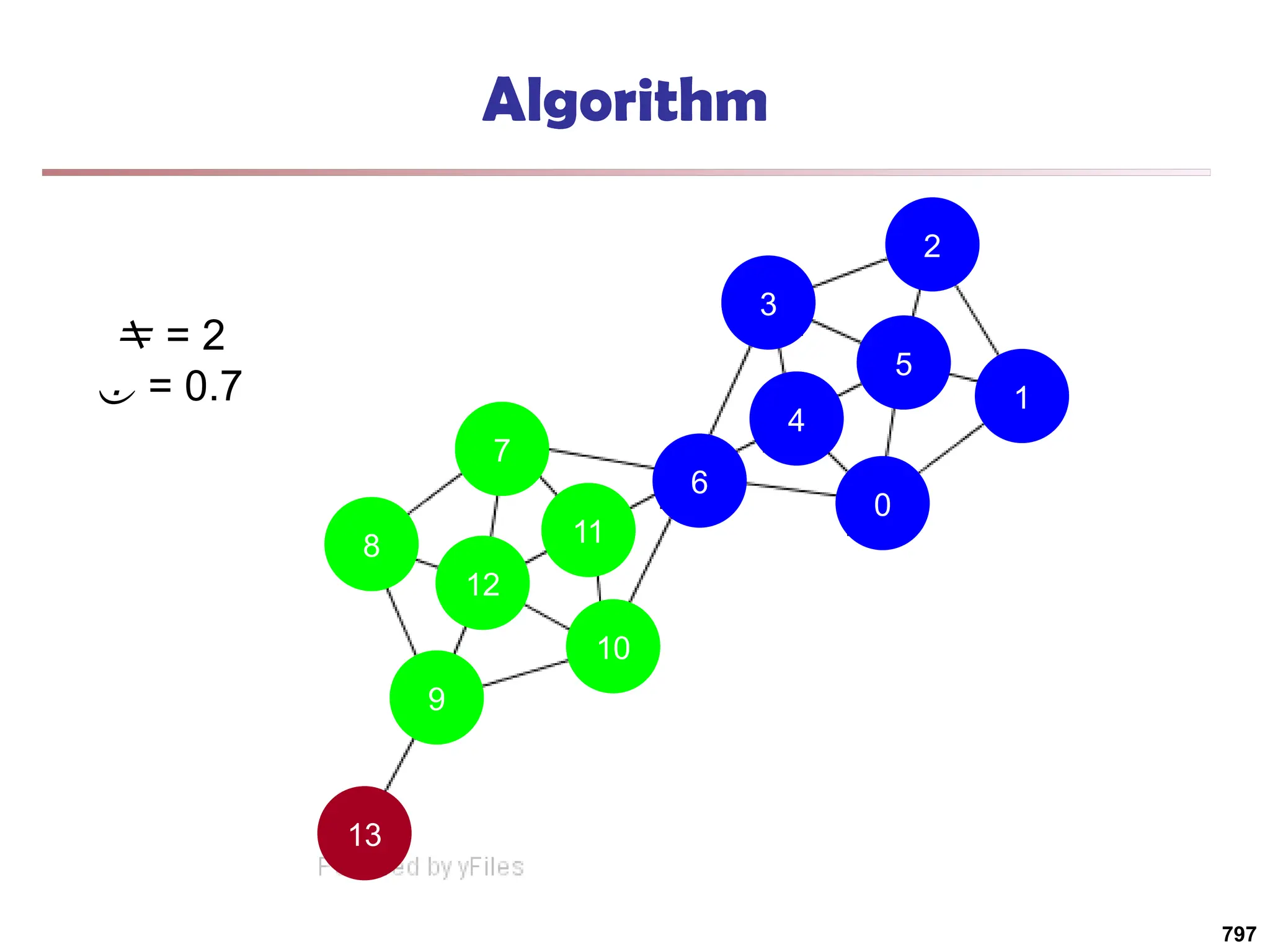
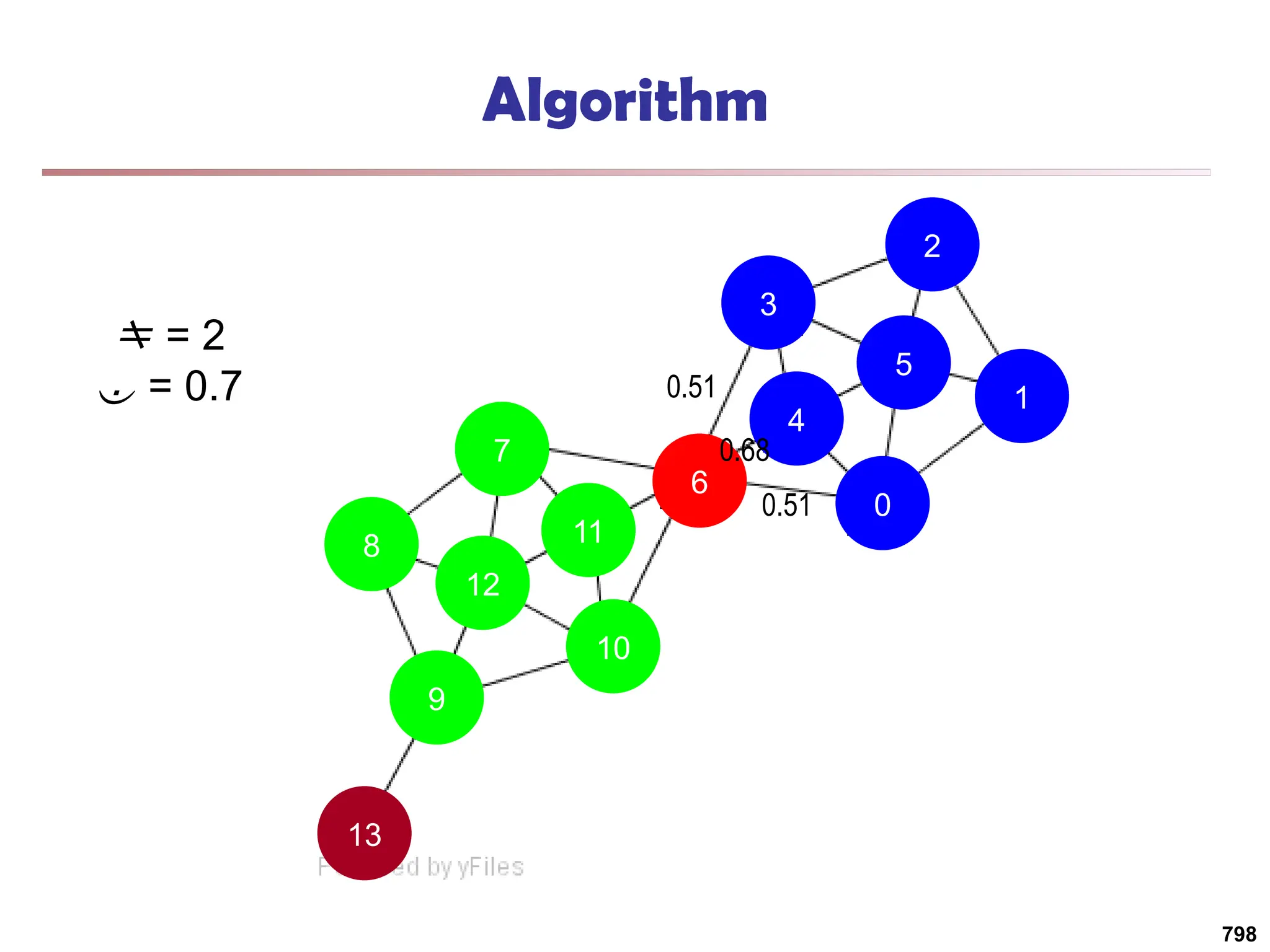
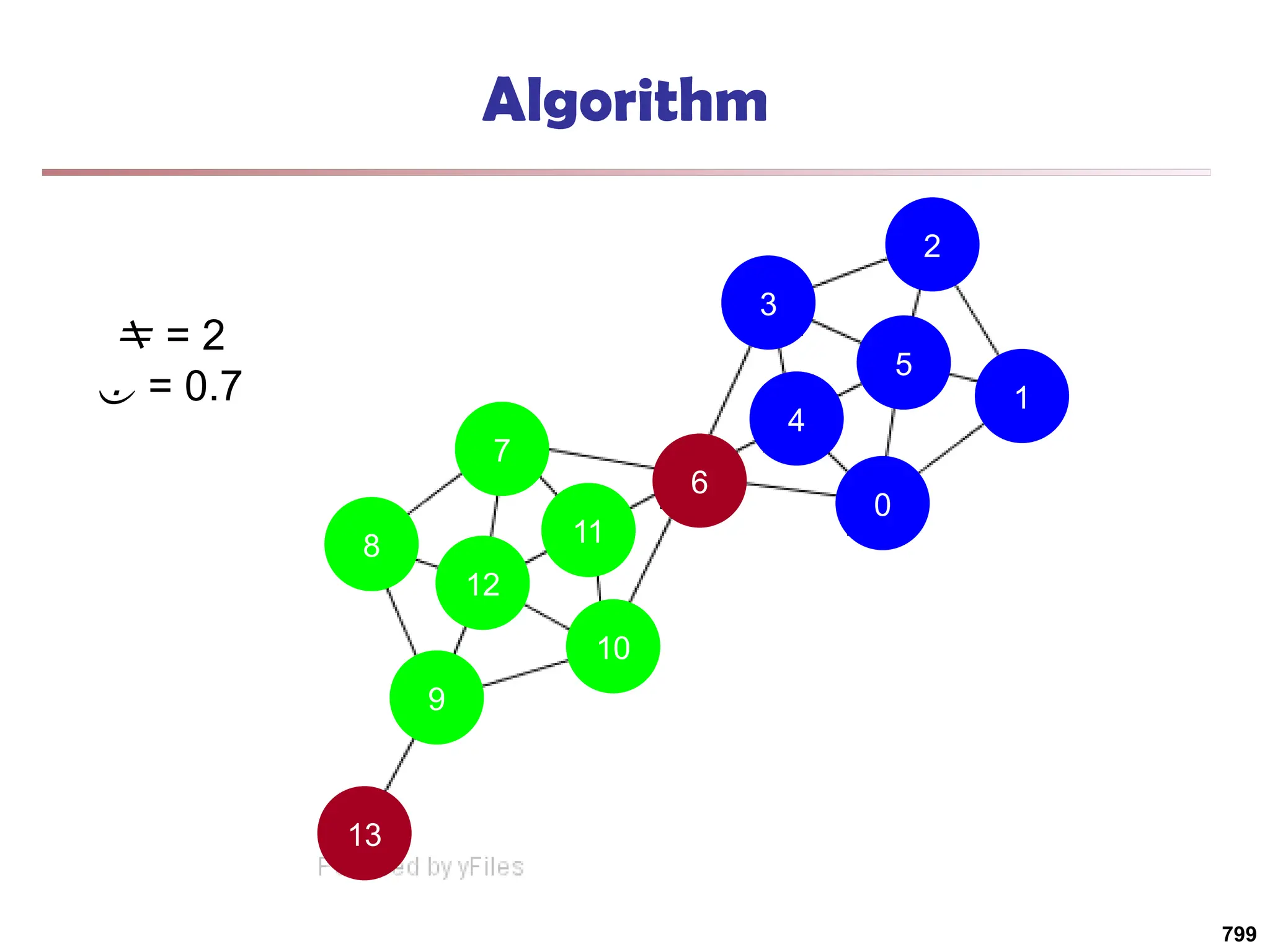
![Running Time
Running time = O(|E|)
For sparse networks = O(|V|)
[2] A. Clauset, M. E. J. Newman, & C. Moore, Phys. Rev. E 70, 066111 (2004).
800](https://image.slidesharecdn.com/dwdm3rdeditiontextbookslides-241024155956-ed696a42/75/DWDM-3rd-EDITION-TEXT-BOOK-SLIDES24-pptx-798-2048.jpg)




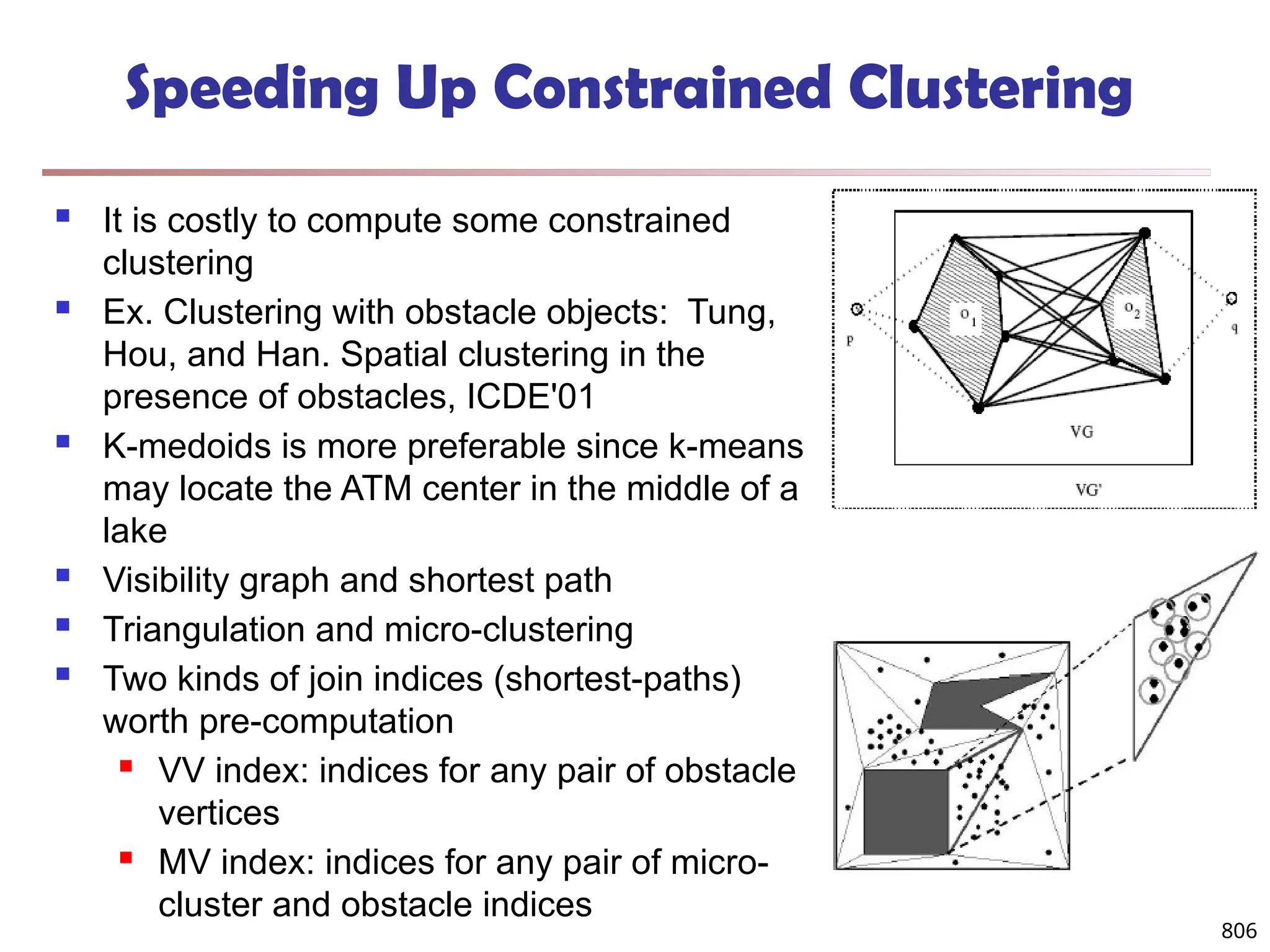

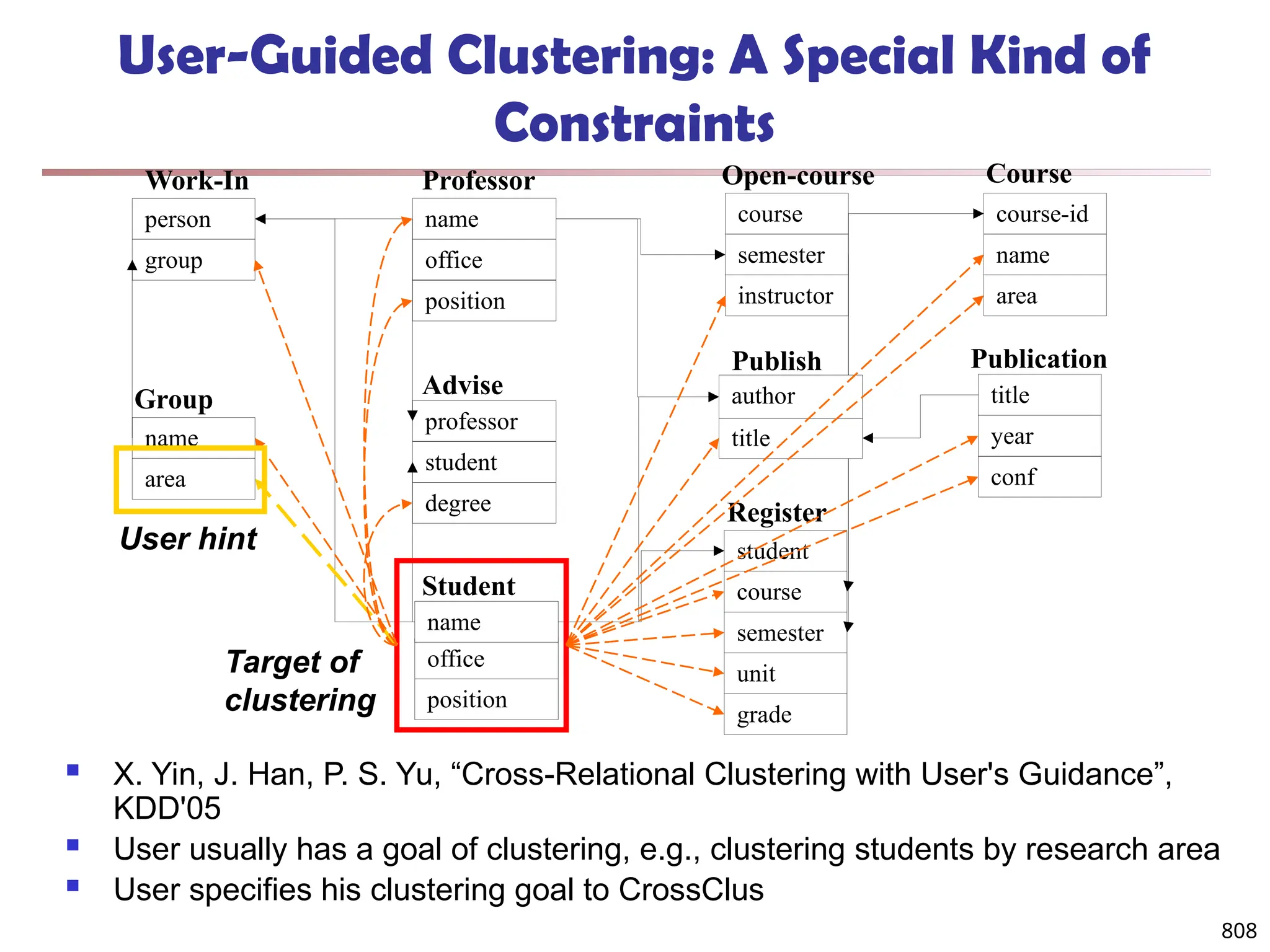


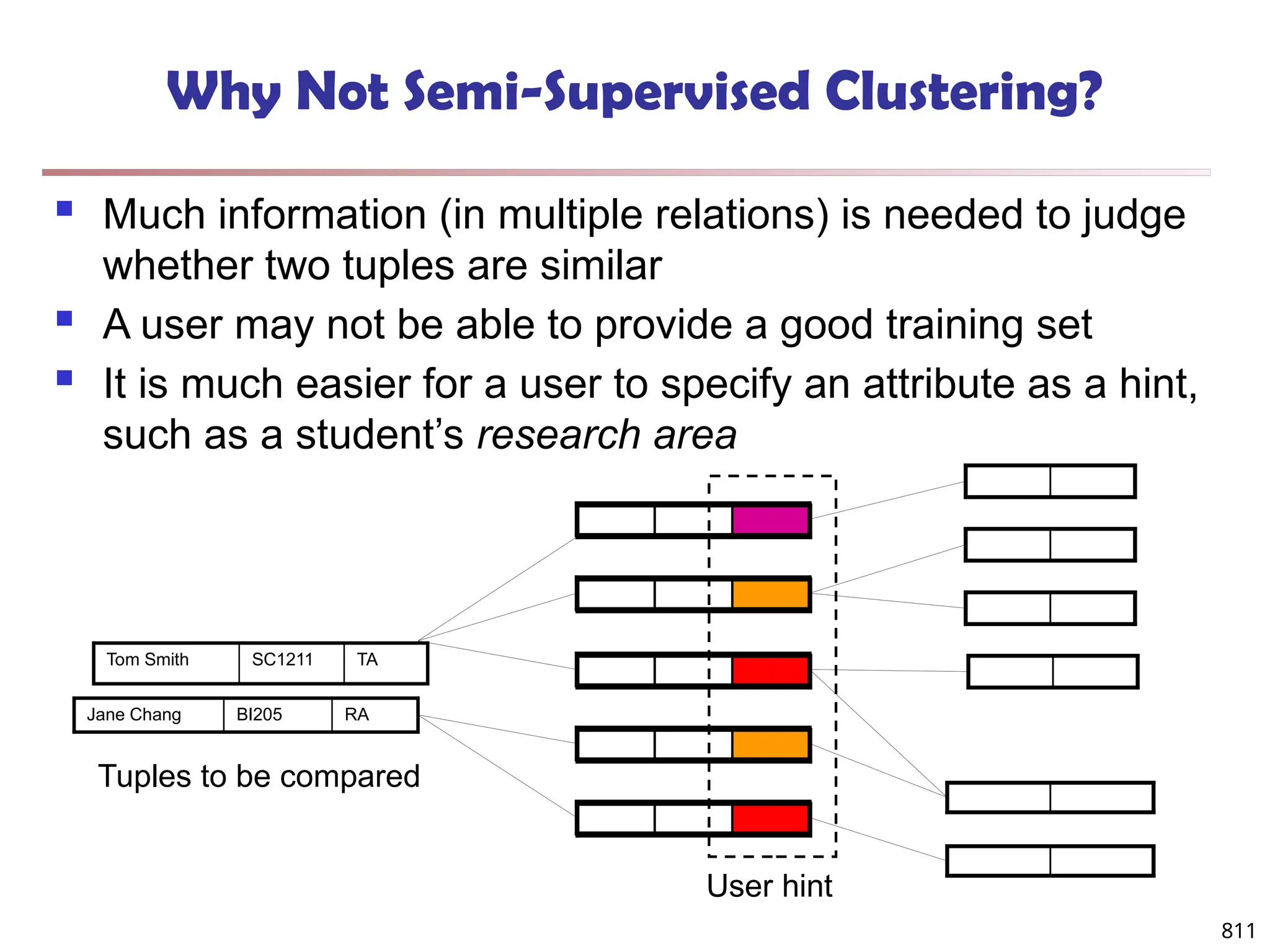

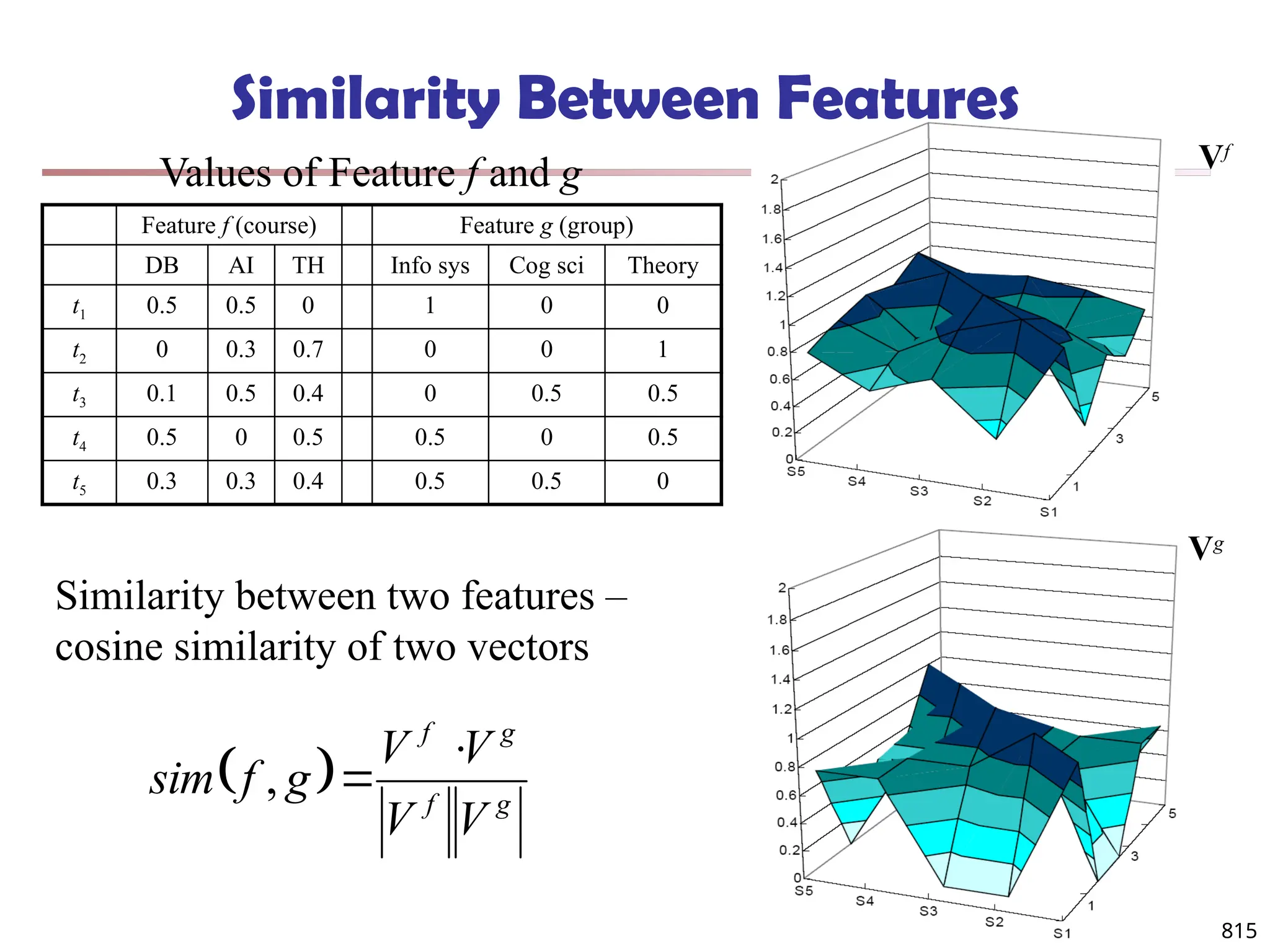
![813
Multi-Relational Features
A multi-relational feature is defined by:
A join path, e.g., Student → Register → OpenCourse → Course
An attribute, e.g., Course.area
(For numerical feature) an aggregation operator, e.g., sum or average
Categorical feature f = [Student → Register → OpenCourse → Course,
Course.area, null]
Tuple Areas of courses
DB AI TH
t1 5 5 0
t2 0 3 7
t3 1 5 4
t4 5 0 5
t5 3 3 4
areas of courses of each student
Tuple Feature f
DB AI TH
t1 0.5 0.5 0
t2 0 0.3 0.7
t3 0.1 0.5 0.4
t4 0.5 0 0.5
t5 0.3 0.3 0.4
Values of feature f f(t1)
f(t2)
f(t3)
f(t4)
f(t5)
DB
AI
TH](https://image.slidesharecdn.com/dwdm3rdeditiontextbookslides-241024155956-ed696a42/75/DWDM-3rd-EDITION-TEXT-BOOK-SLIDES24-pptx-811-2048.jpg)
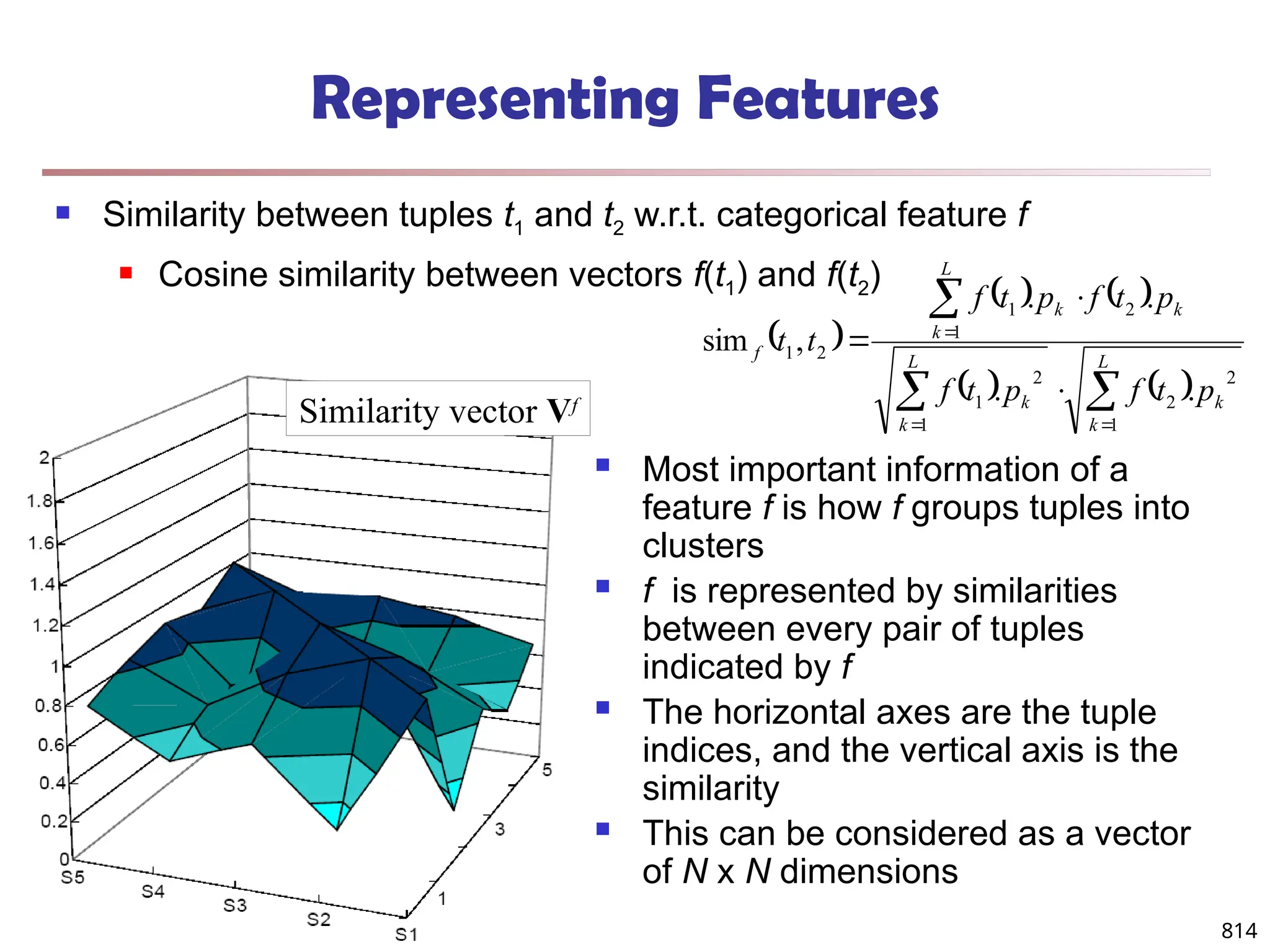

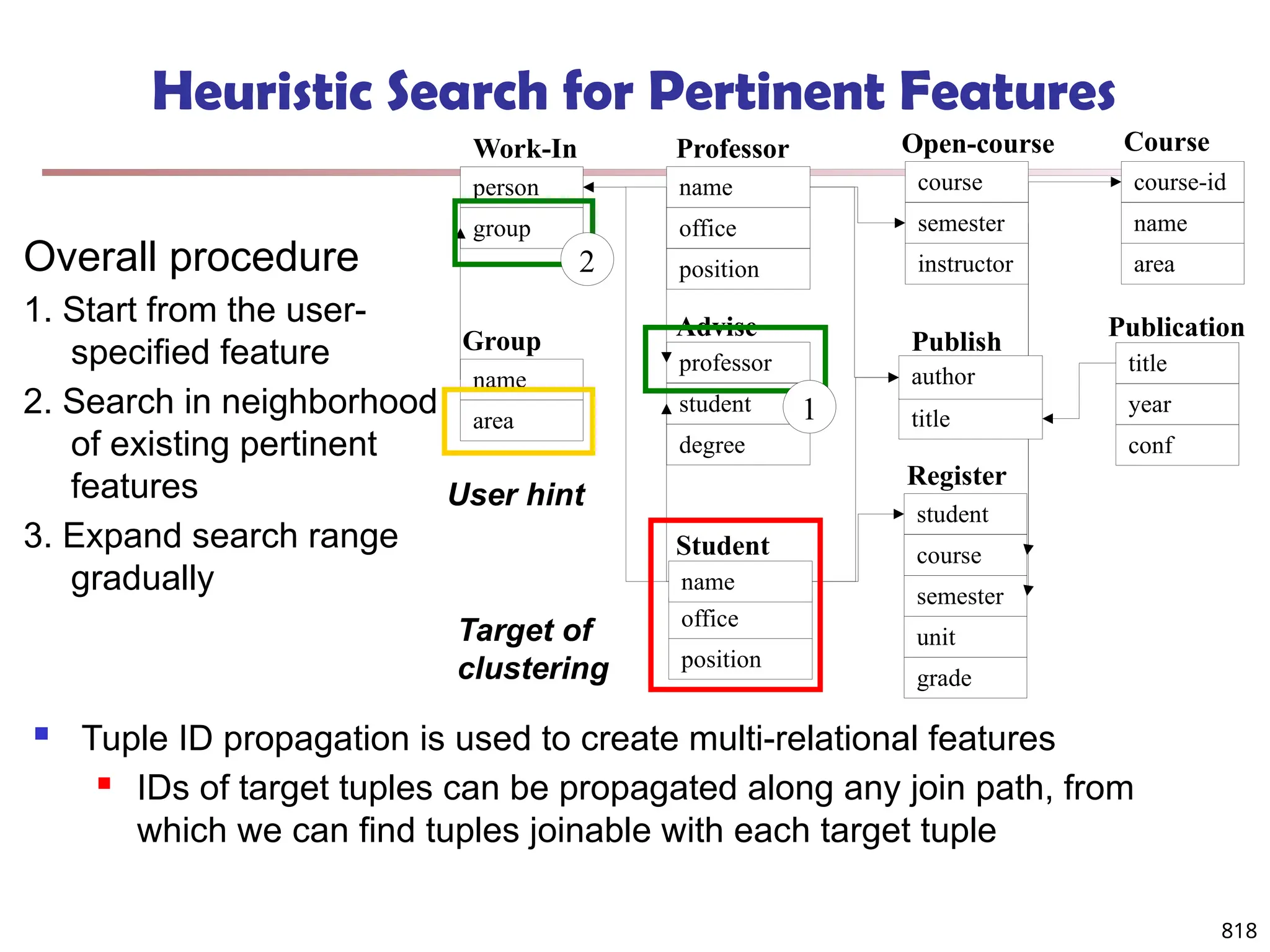
![819
Clustering with Multi-Relational Features
Given a set of L pertinent features f1, …, fL, similarity
between two tuples
Weight of a feature is determined in feature search by
its similarity with other pertinent features
Clustering methods
CLARANS [Ng & Han 94], a scalable clustering
algorithm for non-Euclidean space
K-means
Agglomerative hierarchical clustering
L
i
i
f weight
f
t
t
t
t i
1
2
1
2
1 .
,
sim
,
sim](https://image.slidesharecdn.com/dwdm3rdeditiontextbookslides-241024155956-ed696a42/75/DWDM-3rd-EDITION-TEXT-BOOK-SLIDES24-pptx-817-2048.jpg)
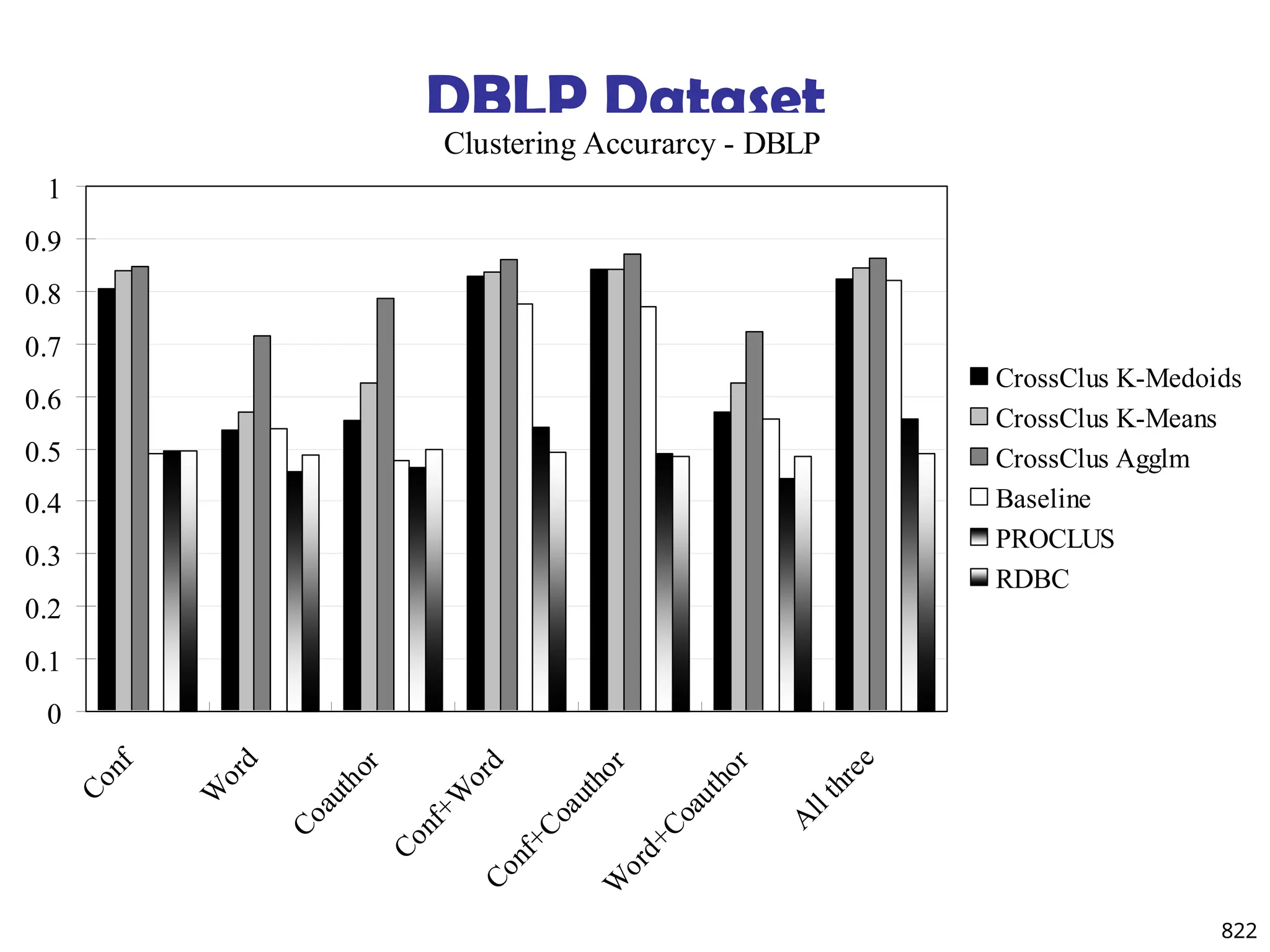
![820
Experiments: Compare CrossClus with
Baseline: Only use the user specified feature
PROCLUS [Aggarwal, et al. 99]: a state-of-the-art
subspace clustering algorithm
Use a subset of features for each cluster
We convert relational database to a table by
propositionalization
User-specified feature is forced to be used in every
cluster
RDBC [Kirsten and Wrobel’00]
A representative ILP clustering algorithm
Use neighbor information of objects for clustering
User-specified feature is forced to be used](https://image.slidesharecdn.com/dwdm3rdeditiontextbookslides-241024155956-ed696a42/75/DWDM-3rd-EDITION-TEXT-BOOK-SLIDES24-pptx-818-2048.jpg)





















































![Approach III: Modeling High-Dimensional Outliers
Ex. Angle-based outliers: Kriegel, Schubert, and Zimek [KSZ08]
For each point o, examine the angle ∆xoy for every pair of points x, y.
Point in the center (e.g., a), the angles formed differ widely
An outlier (e.g., c), angle variable is substantially smaller
Use the variance of angles for a point to determine outlier
Combine angles and distance to model outliers
Use the distance-weighted angle variance as the outlier score
Angle-based outlier factor (ABOF):
Efficient approximation computation method is developed
It can be generalized to handle arbitrary types of data 887
Develop new models for high-
dimensional outliers directly
Avoid proximity measures and adopt
new heuristics that do not deteriorate
in high-dimensional data
A set of points
form a cluster
except c (outlier)](https://image.slidesharecdn.com/dwdm3rdeditiontextbookslides-241024155956-ed696a42/75/DWDM-3rd-EDITION-TEXT-BOOK-SLIDES24-pptx-874-2048.jpg)







![895
Outlier Discovery: Distance-Based Approach
Introduced to counter the main limitations imposed by
statistical methods
We need multi-dimensional analysis without knowing
data distribution
Distance-based outlier: A DB(p, D)-outlier is an object O in
a dataset T such that at least a fraction p of the objects in T
lies at a distance greater than D from O
Algorithms for mining distance-based outliers [Knorr & Ng,
VLDB’98]
Index-based algorithm
Nested-loop algorithm
Cell-based algorithm](https://image.slidesharecdn.com/dwdm3rdeditiontextbookslides-241024155956-ed696a42/75/DWDM-3rd-EDITION-TEXT-BOOK-SLIDES24-pptx-882-2048.jpg)