Dynamic pgmming

Dynamic Programming

Dr. C.V. Suresh Babu

Topics
 What

is Dynamic Programming
 Binomial Coefficient
 Floyd’s Algorithm
 Chained Matrix Multiplication
 Optimal Binary Search Tree
 Traveling Salesperson
2

Why Dynamic Programming?
 Divide-and-Conquer:

a top-down approach.
 Many smaller instances are computed more
than once.
 Dynamic

programming: a bottom-up approach.
 Solutions for smaller instances are stored in a
table for later use.
3

Dynamic Programming







An Algorithm Design Technique
A framework to solve Optimization problems
Elements of Dynamic Programming
Dynamic programming version of a recursive
algorithm.
Developing a Dynamic Programming Algorithm
–

Example: Multiplying a Sequence of Matrices

4

Why Dynamic Programming?
• It sometimes happens that the natural way of dividing an
instance suggested by the structure of the problem leads us to
consider several overlapping subinstances.
• If we solve each of these independently, they will in turn
create a large number of identical subinstances.
• If we pay no attention to this duplication, it is likely that we
will end up with an inefficient algorithm.
• If, on the other hand, we take advantage of the duplication and
solve each subinstance only once, saving the solution for later
use, then a more efficient algorithm will result.
5

Why Dynamic Programming? …
The underlying idea of dynamic programming is
thus quite simple: avoid calculating the same thing
twice, usually by keeping a table of known results,
which we fill up as subinstances are solved.
• Dynamic programming is a bottom-up technique.
• Examples:
1) Fibonacci numbers
2) Computing a Binomial coefficient
6

Dynamic Programming

• Dynamic Programming is a general algorithm design
technique.
• Invented by American mathematician Richard Bellman in
the 1950s to solve optimization problems.
• “Programming” here means “planning”.
• Main idea:
• solve several smaller (overlapping) subproblems.
• record solutions in a table so that each subproblem is
only solved once.
• final state of the table will be (or contain) solution. 7

Dynamic Programming
 Define

a container to store intermediate

results
 Access container versus recomputing results
 Fibonacci
–

numbers example (top down)

Use vector to store results as calculated so they
are not re-calculated
8

Dynamic Programming
 Fibonacci

numbers:
0, 1, 1, 2, 3, 5, 8, 13, 21, 24

 Recurrence

Relation of Fibonacci numbers

?
9

Example: Fibonacci numbers
• Recall definition of Fibonacci numbers:
f(0) = 0
f(1) = 1
f(n) = f(n-1) + f(n-2)

for n ≥ 2

• Computing the nth Fibonacci number recursively (topdown):
f(n)
f(n-1)
f(n-2)

+

+
f(n-3)

f(n-2)
f(n-3)

+

f(n-4)

10

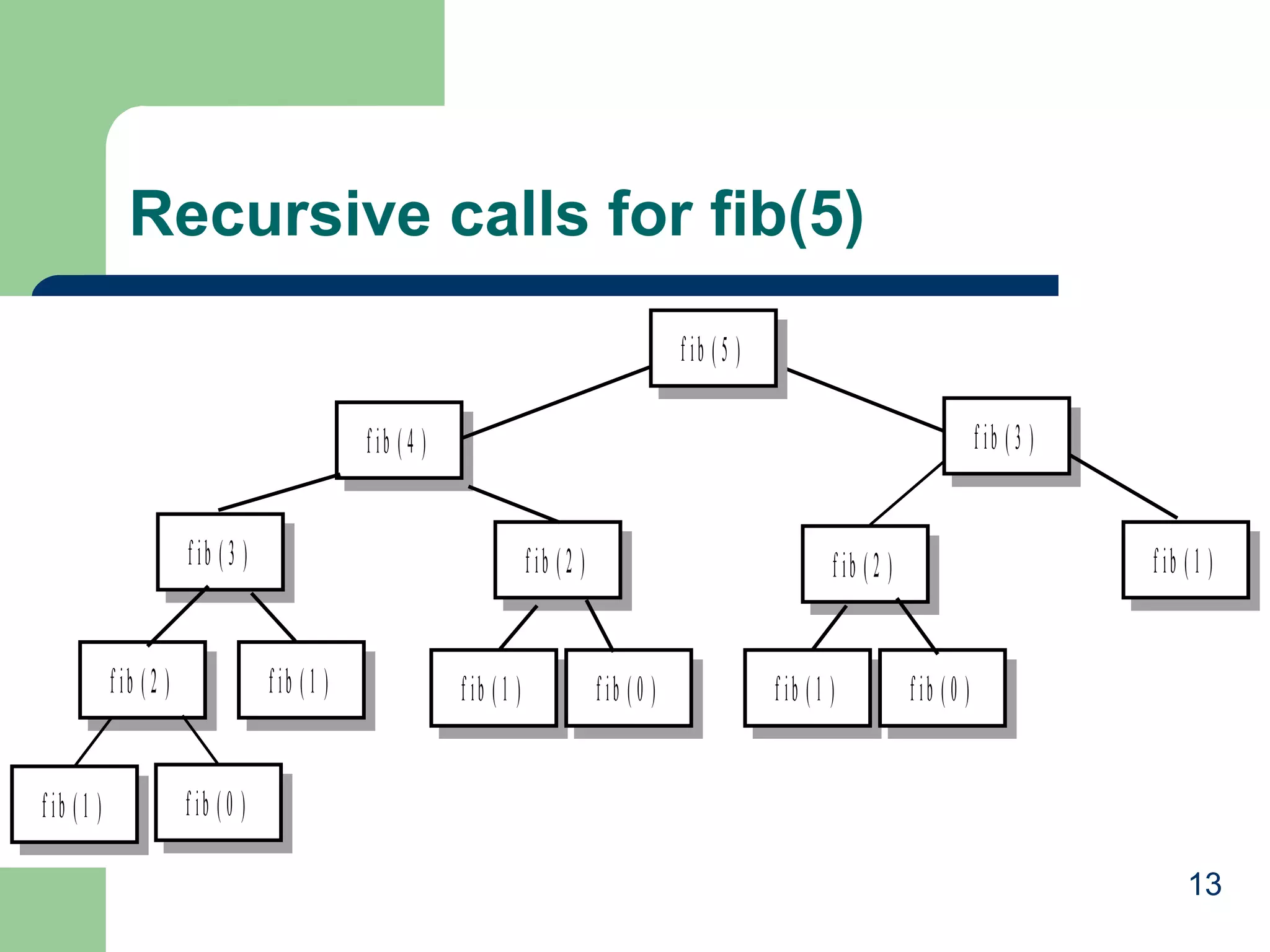
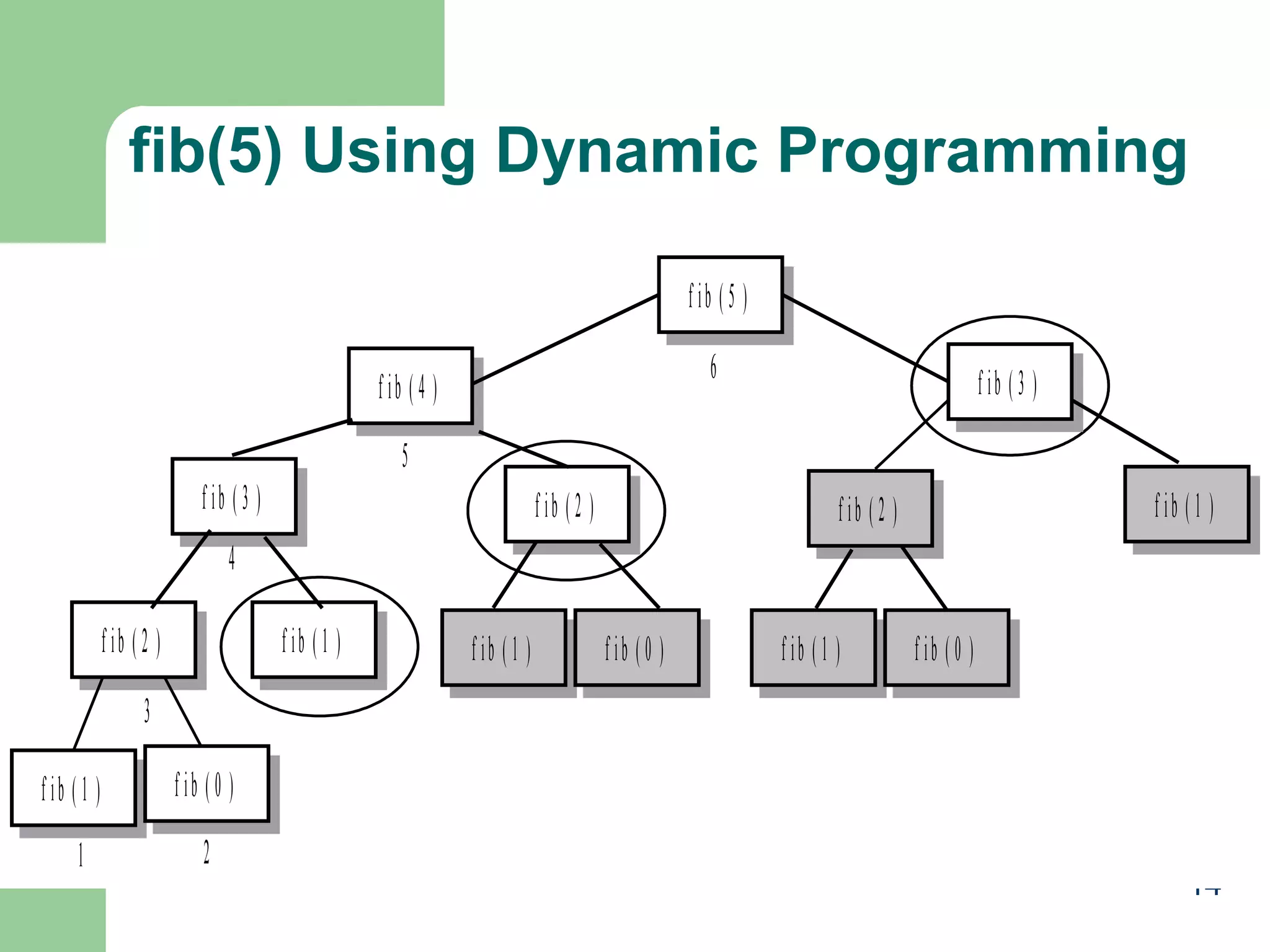
Fib vs. fibDyn
int fib(int n) {
if (n <= 1)
return n; // stopping conditions
else return fib(n-1) + fib(n-2);
// recursive step
}
int fibDyn(int n, vector<int>& fibList) {
int fibValue;
if (fibList[n] >= 0) // check for a previously computed result and return
return fibList[n];
// otherwise execute the recursive algorithm to obtain the result
if (n <= 1)
// stopping conditions
fibValue = n;
else
// recursive step
fibValue = fibDyn(n-1, fibList) + fibDyn(n-2, fibList);
// store the result and return its value
fibList[n] = fibValue;
return fibValue;
}

11

Example: Fibonacci numbers
Computing the nth fibonacci number using bottom-up
iteration:
• f(0) = 0
• f(1) = 1
• f(2) = 0+1 = 1
• f(3) = 1+1 = 2
• f(4) = 1+2 = 3
• f(5) = 2+3 = 5
•
•
•
• f(n-2) = f(n-3)+f(n-4)
• f(n-1) = f(n-2)+f(n-3)
• f(n) = f(n-1) + f(n-2)

12

Recursive calls for fib(5)
f ib ( 5 )
f ib ( 3 )

f ib ( 4 )
f ib ( 3 )

f ib ( 2 )
f ib ( 1 )

f ib ( 2 )
f ib ( 1 )

f ib ( 1 )

f ib ( 1 )

f ib ( 2 )
f ib ( 0 )

f ib ( 1 )

f ib ( 0 )

f ib ( 0 )
13

fib(5) Using Dynamic Programming
f ib ( 5 )
6

f ib ( 4 )

f ib ( 3 )

5
f ib ( 3 )

f ib ( 2 )

f ib ( 1 )

f ib ( 2 )

4
f ib ( 2 )

f ib ( 1 )

f ib ( 1 )

f ib ( 0 )

f ib ( 1 )

f ib ( 0 )

3
f ib ( 1 )

f ib ( 0 )

1

2

14

Statistics (function calls)
fib

fibDyn

N = 20

21,891

39

N = 40

331,160,281

79

15

Top down vs. Bottom up
 Top

down dynamic programming moves
through recursive process and stores results
as algorithm computes
 Bottom up dynamic programming evaluates
by computing all function values in order,
starting at lowest and using previously
computed values.
16

Examples of Dynamic Programming Algorithms
• Computing binomial coefficients
• Optimal chain matrix multiplication
• Floyd’s algorithms for all-pairs shortest paths
• Constructing an optimal binary search tree
• Some instances of difficult discrete optimization problems:
• travelling salesman
• knapsack
17

A framework to solve Optimization problems
 For
–
–
–

each current choice:

Determine what subproblem(s) would remain if this
choice were made.
Recursively find the optimal costs of those
subproblems.
Combine those costs with the cost of the current
choice itself to obtain an overall cost for this choice

 Select

a current choice that produced the
minimum overall cost.
18

Elements of Dynamic Programming


Constructing solution to a problem by building it up
dynamically from solutions to smaller (or simpler) subproblems
–

–

sub-instances are combined to obtain sub-instances of
increasing size, until finally arriving at the solution of the
original instance.
make a choice at each step, but the choice may depend on the
solutions to sub-problems.

19

Elements of Dynamic Programming …



Principle of optimality
–



the optimal solution to any nontrivial instance of a problem is a
combination of optimal solutions to some of its sub-instances.

Memorization (for overlapping sub-problems)
–
–

avoid calculating the same thing twice,
usually by keeping a table of know results that fills up as subinstances are solved.

20

Development of a dynamic programming
algorithm








Characterize the structure of an optimal solution
– Breaking a problem into sub-problem
– whether principle of optimality apply
Recursively define the value of an optimal solution
– define the value of an optimal solution based on value of solutions
to sub-problems
Compute the value of an optimal solution in a bottom-up fashion
– compute in a bottom-up fashion and save the values along the
way
– later steps use the save values of pervious steps
Construct an optimal solution from computed information
21

Binomial Coefficient


Binomial coefficient:
n 
n!
 =
k  k!( n −k )!
 





for 0 ≤ k ≤ n

Cannot compute using this formula because of
n!
Instead, use the following formula:

22

Binomial Using Divide & Conquer


Binomial formula:

  n − 1   n − 1
C
 k − 1 + C  k  0 < k < n
 

 n  
 

C  = 
k
 n
 n
  
1
k = 0 or k = n (C   or C   )
 0
 n

 
 

23

Binomial using Dynamic Programming



Just like Fibonacci, that formula is very inefficient
Instead, we can use the following:

(a + b) n = C (n,0)a n + ... + C (n, i )a n −i b i + ... + C (n, n)b n

24

Bottom-Up
 Recursive
–

B[i] [j] =

property:
B[i – 1] [j – 1] + B[i – 1][j] 0 < j < i
1

j = 0 or j = i

25

Pascal’s Triangle
0

1

0

1

1

1

1

2

1

2

1

3

1

3

3 1

4

1

4

6 4

…
i
n

2

3 4

…

j

k

1
B[i-1][j-1]+ B[i-1][j]
B[i][j]
26



Record the values in a table of n+1 rows and k+1 columns

0

1

2

0

1
1

2

1

3

3

k

1

3

k-1

1

2

…

1

1

3

1

...
k

1

1

…
n-1

1

n

1

 n − 1
C
 k − 1




 n − 1
C
k 



n 
C 
k 
 

27

ALGORITHM Binomial(n,k)
//Computes C(n, k) by the dynamic programming algorithm
//Input: A pair of nonnegative integers n ≥ k ≥ 0
//Output: The value of C(n ,k)
for i 0 to n do
for j 0 to min (i ,k) do
if j = 0 or j = k
C [i , j]  1
else C [i , j]  C[i-1, j-1] + C[i-1, j]
return C [n, k]
k

i −1

A( n, k ) = ∑∑1 +
i =1 j =1

=

n

k

k

n

i =1

i =K +1

∑ ∑1 = ∑(i −1) + ∑k

i =k +1 j =1

( k −1) k
+ k ( n − k ) ∈Θ( nk )
2

28

Floyd’s Algorithm: All pairs shortest paths
•Find shortest path when direct path doesn’t exist
•In a weighted graph, find shortest paths between every pair of
vertices
• Same idea: construct solution through series of matrices
D(0), D(1), … using an initial subset of the vertices as
4
3
intermediaries.
1
• Example:
1
6
1

5

2

3

4

29

Shortest Path





Optimization problem – more than one candidate for
the solution
Solution is the candidate with optimal value
Solution 1 – brute force
–
–



Find all possible paths, compute minimum
Efficiency?
Worse than O(n2)

Solution 2 – dynamic programming
–
–

Algorithm that determines only lengths of shortest paths
Modify to produce shortest paths as well
30

Example
1

2

3

4

5

1

2

3

4

5

1

0

1

∞

1

5

1

0

1

3

1

4

2

9

0

3

2

∞

2

8

0

3

2

5

3

∞

∞

0

4

∞

3

10 11

0

4

7

4

∞

∞

2

0

3

4

6

7

2

0

3

5

3

∞

∞

∞

0

5

3

4

6

4

0

W - Graph in adjacency matrix

D - Floyd’s algorithm

31

Meanings









D(0)[2][5] = lenth[v2, v5]= ∞
D(1)[2][5] = minimum(length[v2,v5], length[v2,v1,v5])
= minimum (∞, 14) = 14
D(2)[2][5] = D(1)[2][5] = 14
D(3)[2][5] = D(2)[2][5] = 14
D(4)[2][5] = minimum(length[v2,v1,v5], length[v2,v4,v5]),
length[v2,v1,v5], length[v2, v3,v4,v5]),
= minimum (14, 5, 13, 10) = 5
D(5)[2][5] = D(4)[2][5] = 5
32

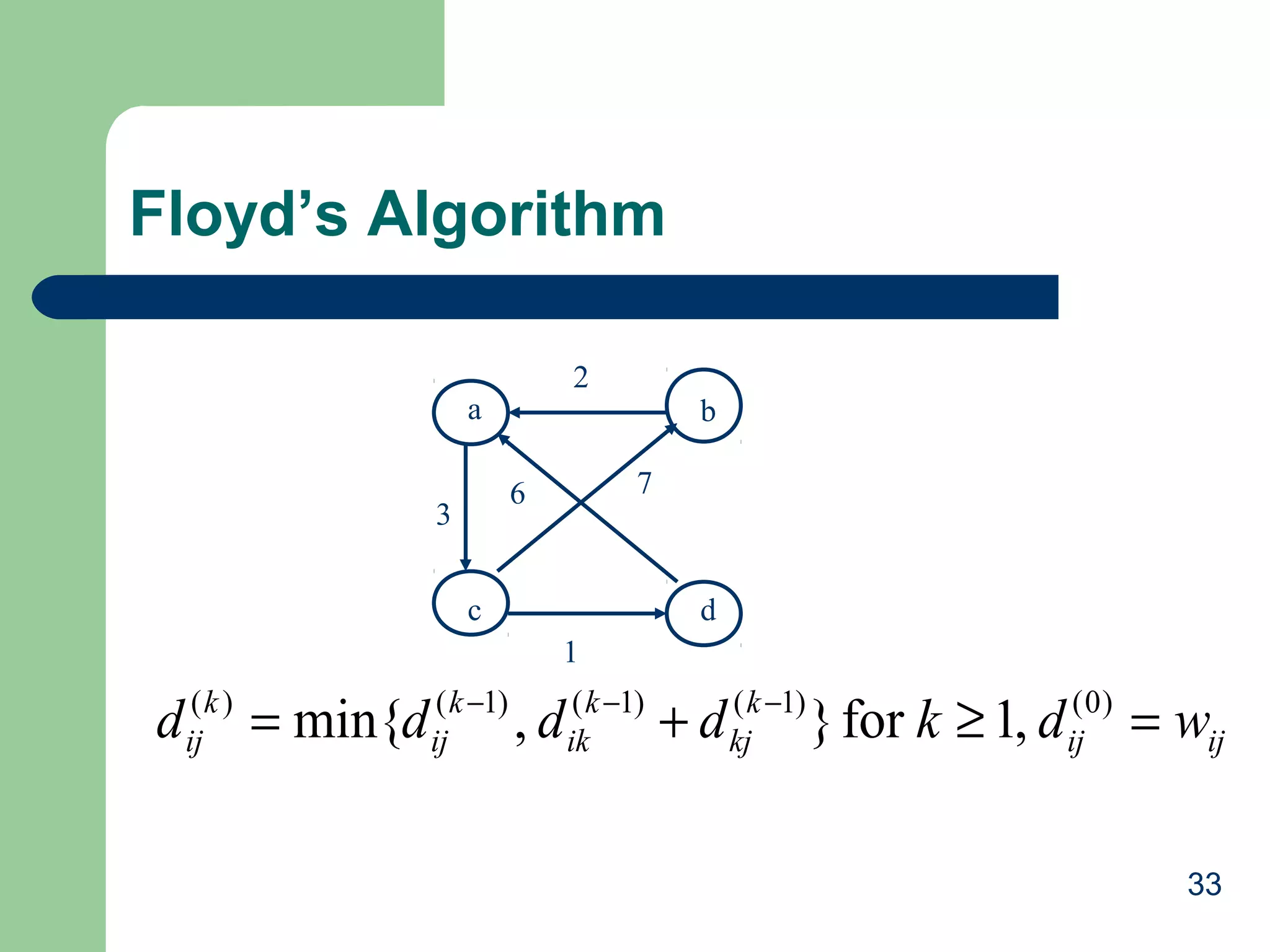
Floyd’s Algorithm
2

a

7

6

3

b

c

d
1

(
(
(
(
(
d ijk ) = min{d ijk −1) , d ikk −1) + d kjk −1) } for k ≥ 1, d ij0 ) = wij

33

Computing D
 D(0)

=W
 Now compute D(1)
 Then D(2)
 Etc.

34

Floyd’s Algorithm: All pairs shortest paths
• ALGORITHM Floyd (W[1 … n, 1… n])

•For k ← 1 to n do
•For i ← 1 to n do
•For j ← 1 to n do
•W[i, j] ← min{W[i,j], W{i, k] + W[k, j]}
•Return W
•Efficiency = ?

Θ(n)

35

Example: All-pairs shortest-path problem
Example: Apply Floyd’s algorithm to find the t Allpairs shortest-path problem of the digraph defined by
the following weight matrix
0
6
∞
∞
3

2
0
∞
∞
∞

∞
3
0
2
∞

1
2
4
0
∞

8
∞
∞
3
0

36

Visualizations




http://www.ifors.ms.unimelb.edu.au/tutorial/path/#list
http://www1.math.luc.edu/~dhardy/java/alg/floyd.html
http://students.ceid.upatras.gr/%7Epapagel/project/kef5_7_2.htm

37

Chained Matrix Multiplication


Problem: Matrix-chain multiplication
– a chain of <A1, A2, …, An> of n matrices
–






find a way that minimizes the number of scalar multiplications to
compute the product A1A2…An

Strategy:
Breaking a problem into sub-problem
– A1A2...Ak, Ak+1Ak+2…An
Recursively define the value of an optimal solution
– m[i,j] = 0 if i = j
– m[i,j]= min{i<=k<j} (m[i,k]+m[k+1,j]+pi-1pkpj)
–

for 1 <= i <= j <= n

38

Example
 Suppose

we want to multiply a 2x2 matrix
with a 3x4 matrix
 Result is a 2x4 matrix
 In general, an i x j matrix times a j x k matrix
requires i x j x k elementary multiplications

39

Example


Consider multiplication of four matrices:
A
(20 x 2)



x

B
(2 x 30)

x

C
(30 x 12)

x

D
(12 x 8)

Matrix multiplication is associative
A(B (CD)) = (AB) (CD)



Five different orders for multiplying 4 matrices
1.
2.
3.
4.
5.

A(B (CD)) = 30*12*8 + 2*30*8 + 20*2*3 = 3,680
(AB) (CD) = 20*2*30 + 30*12*8 + 20*30*8 = 8,880
A ((BC) D) = 2*30*12 + 2*12*3 + 20*2*8 = 1,232
((AB) C) D = 20*2*30 + 20*30*12 + 20*12*8 = 10,320
(A (BC)) D = 2*30*12 + 20*2*12 + 20*12*8 = 3,120
40

Algorithm
int minmult (int n, const ind d[], index P[ ] [ ])
{
index i, j, k, diagonal;
int M[1..n][1..n];
for (i = 1; i <= n; i++)
M[i][i] = 0;
for (diagonal = 1; diagonal <= n-1; diagonal++)
for (i = 1; i <= n-diagonal; i++)
{
j = i + diagonal;
M[i] [j] = minimum(M[i][k] + M[k+1][j] + d[i-1]*d[k]*d[j]);
// minimun (i <= k <= j-1)
P[i] [j] = a value of k that gave the minimum;
}
return M[1][n];
}

41

Optimal Binary Trees
 Optimal

way of constructing a binary search

tree
 Minimum depth, balanced (if all keys have
same probability of being the search key)
 What if probability is not all the same?
 Multiply probability of accessing that key by
number of links to get to that key
42

Example
If p1 = 0.7
Key3

p2 = 0.2

3(0.7) + 2(0.2) + 1(0.1)
= 2.6

p3 = 0.1
key2

Θ (n3) Efficiency

key1

43

Traveling Salesperson
 The

Traveling Salesman Problem (TSP) is a
deceptively simple combinatorial problem. It
can be stated very simply:
 A salesman spends his time visiting n cities
(or nodes) cyclically. In one tour he visits
each city just once, and finishes up where he
started. In what order should he visit them to
minimize the distance traveled?
44

Why study?






The problem has some direct importance, since
quite a lot of practical applications can be put in this
form.
It also has a theoretical importance in complexity
theory, since the TSP is one of the class of "NP
Complete" combinatorial problems.
NP Complete problems are intractable in the sense
that no one has found any really efficient way of
solving them for large n.
–

They are also known to be more or less equivalent to each
other; if you knew how to solve one kind of NP Complete
problem you could solve the lot.
45

Efficiency
 The

holy grail is to find a solution algorithm
that gives an optimal solution in a time that
has a polynomial variation with the size n of
the problem.
 The best that people have been able to do,
however, is to solve it in a time that varies
exponentially with n.
46

Later…
 We’ll

get back to the traveling salesperson
problem in the next chapter….

47

Animations
 http://www.pcug.org.au/~dakin/tsp.htm

 http://www.ing.unlp.edu.ar/cetad/mos/TSPBIB_hom

48

Chapter Summary
• Dynamic programming is similar to divide-andconquer.
• Dynamic programming is a bottom-up approach.
• Dynamic programming stores the results (small
instances) in the table and reuses it instead of
recomputing it.
• Two steps in development of a dynamic
programming algorithm:
• Establish a recursive property
• Solve an instance of the problem in a bottom-up 49

Rules of Sudoku
• Place a number (1-9) in each blank cell.
• Each row (nine lines from left to right), column (also
nine lines from top to bottom) and 3x3 block bounded
by bold line (nine blocks) contains number from 1
through 9.

51

Dynamic pgmming

More Related Content

What's hot

Viewers also liked

Similar to Dynamic pgmming

More from Dr. C.V. Suresh Babu

Recently uploaded

Dynamic pgmming

Editor's Notes