Fp in scala part 1

FP in Scala
into the rabbit hole (part 1)

Introduction
● This is mostly about Functional programming
● This is not about Scala language, but we will
go through them when we are run into
language features
● A lot of my examples here comes from the
book Functional programming in Scala

Functional Programming
One famous Chinese saying said: As small the
sparrow is, it has all the vital organs a life
needs.
Let begin with a small “Sparrow”

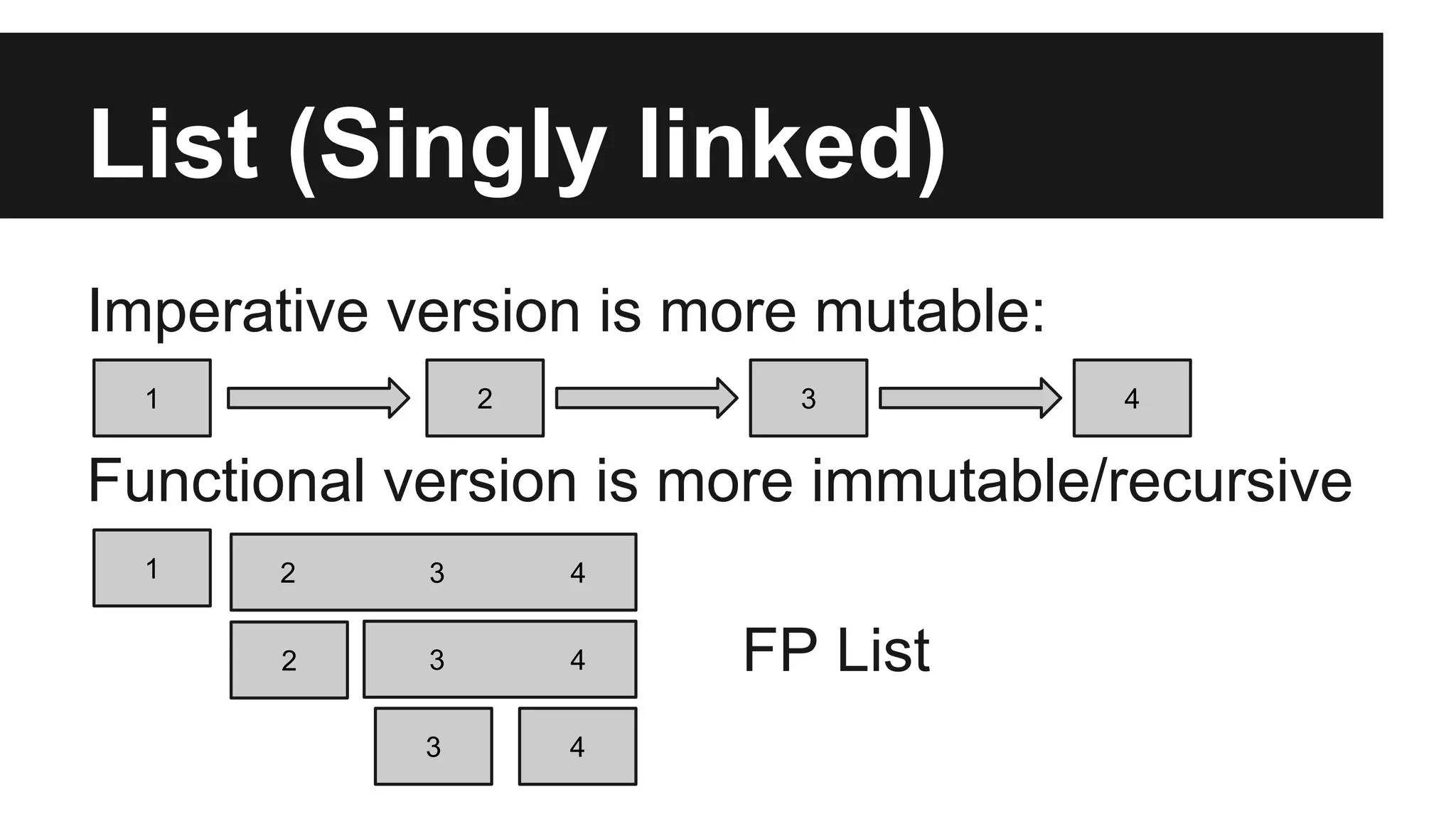
List (Singly linked)
Imperative version is more mutable:
1 2 3 4
Functional version is more immutable/recursive
FP List
1
2 3 4
2
3 4
3 4

Algebraic Data Type
We model List as one Algebraic Data Type
In scala ADT are modeled mostly as sealed
trait and case classes extends from it. Look at
the next slide

pure FP List
sealed trait List[+A]
case object Nil extends List[Nothing]
case class Cons[+A] (head: A, tail: List[A]) extends List[A]
object List {
def apply[A](as: A*): List[A] =
if (as.isEmpty) Nil
else Cons(as.head, apply(as.tail: _*))
private def asString_internal[A](l: List[A]): String =
l match {
case Nil => ""
case Cons(head,tail) => head.toString + " " + asString_internal(tail)
}
def toString[A](l: List[A]): String =
"[ " + asString_internal(l) + "]"
}

traits
traits in scala is similar to mixins in Ruby
It is contains certain functionality/interface that can be
inherited and used by classes, can have both concrete
methods and abstract methods.
sealed traits means all the class inherit this trait must be in
the same file trait in. This give compiler the power to know
the “full” set of classes inherit the trait.

case class
case class is the special class can be used in
functional programming pattern matching
mechanism.
sealed traits and case class are the standard
way in scala to model Algebraic Data Type,
which will be the fundamental building blocks of
functional programming

companion object
object in scala is basically singleton object in
other language.
You can have a companion object with same
name of the class/trait in scala, companion
object can have access of the private
method/data of the class/trait it associated to.
Here we mostly use it as a module for the ADT.

List ADT
case object Nil extends List[Nothing]
case class Cons[+A] (head: A, tail: List[A]) extends List[A]
Here we define List as a trait, and 2 type of lists
are defined, Nil as empty List, and Cons as
non-empty List.

Type Variance
A is just abstract type (generic)
+A here is called covariant, means that if A` is
A’s subtype, then List[A`] is List[A]’s subtype.

Constructor
object List {
if (as.isEmpty) Nil
…
You can create constructor for the List trait with
different signatures here, you can have multiple
constructor here in companion object.

Pattern Matching
private def asString_internal[A](l: List[A]): String =
l match {
case Nil => ""
}
def toString[A](l: List[A]): String =
"[ " + asString_internal(l) + "]"
}
Now we define toString function here, we here use pattern
matching to see what is the remaining list type between Nil
and Cons. Pattern Matching is a very powerful feature in
FP, and it can match into the multiple layers of objects,
match types and much more.

Recursive
You can also notice that we use recursive here,
recursive is preferred in FP to loops. And will
avoid mutables. In scala as it is based on Java
ByteCode, it is still possible to stack overflow,
so we sometime will need to try to do tail
recursion as much as possible, we will talk
about it later.

Scala is not Pure FP
As we can see in early slide, we now have a minimum
functional List, it does not really use OO concepts (trait and
case class here only use to model ADT). This is kind of
pure FP way to do the function programming: A few types
and functions that work on the types.
If you look at scala doc for their List, it kind of different and
toString is directly a method of List. It is in fact more OO/FP
hybride way to do it. Let change to that and see.

OO/FP List
sealed trait List[+A] {
def head: A
def tail: List[A]
def isEmpty: Boolean
override def toString = "[ " + asString_internal(this) + "]"
private def asString_internal[B >: A](l: List[B]): String =
l match {
case _ => ""
}
}
object List {
if (as.isEmpty) Nil
}
case object Nil extends List[Nothing] {
override def isEmpty = true
override def head: Nothing =
throw new NoSuchElementException("head of empty list")
override def tail: List[Nothing] =
throw new UnsupportedOperationException("tail of empty
list")
}
case class Cons[+A] (hd: A, tl: List[A]) extends List[A] {
override def isEmpty = false
override def head : A = hd
override def tail : List[A] = tl
}

lower bound (Type variation)
asString_internal[B >: A](l: List[B]): String
Here the B >: A is called lower bound in type variation,
which means that, B must be a supertype of A. This is
required to satisfy the type variance check (you can not use
A here directly in place of B)
check this

More List functions
def sum(ints: List[Int]): Int = ints match {
case Nil => 0
case Cons(x,xs) => x + sum(xs)
}
def product(ds: List[Double]): Double = ds match {
case Nil => 1.0
case Cons(0.0, _) => 0.0
case Cons(x,xs) => x * product(xs)
}
These 2 common functions seems really
similar, how we can generalize it.

foldRight
def foldRight[A,B](l: List[A], z: B)(f: (A, B) => B): B =
l match {
case Nil => z
case Cons(x, xs) => f(x, foldRight(xs, z)(f))
}
def sum(l: List[Int]) =
foldRight(l, 0)((x,y) => x + y)
def product(l: List[Double]) =
foldRight(l, 1.0)(_ * _)
Here is the higher order function (function take function as
parameter or output), a very power/interesting feature in
FP. Here _ * _ means the first parameter * second
parameter, which is a short hand way to write it.

tail recursion
foldRight is abstract and powerful, but it can stack overflow,
what can we do?
@annotation.tailrec
def foldLeft[A,B](l: List[A], z: B)(f: (B, A) => B): B = l match {
case Nil => z
case Cons(h,t) => foldLeft(t, f(z,h))(f)
}
def reverse[A](l: List[A]): List[A] = foldLeft(l, List[A]())((acc,h) => Cons(h,acc))
def foldRight[A,B](l: List[A], z: B)(f: (A,B) => B): B =
foldLeft(reverse(l), z)((b,a) => f(a,b))
foldLeft is tail recursive, and it enforced (by the annotation)
to optimize into loop in background, then we can use this
FoldLeft to implement FoldRight (now no stack overflow

map
You should be familiar with map on List
def map[A, B](la: List[A])(f: A => B): List[B] =
foldRight(la, Nil:List[B])((h,t) => Cons(f(h), t))
val a = List(1,2,3,4)
List.map(a)(_+1)
we get
List(2,3,4,5)

There are far more than map
def unit[A](a: A): List[A] =
Cons(a, Nil)
def flatMap[A, B](la: List[A])(f: A => List[B]): List[B] =
concat(foldRight(la, Nil:List[List[B]])((h,t) => Cons(f(h),t)))
def join[A](lla: List[List[A]]): List[A] =
flatMap(lla)(la => la)
def compose[A,B,C](f: A => List[B], g: B => List[C]): A => List[C] =
a => flatMap(f(a))(g)
def apply[A,B](la: List[A])(f: List[A => B]): List[B] =
flatMap(f)(t1 => flatMap(la)(t2 => unit(t1(t2))))
def map2[A,B,C](la: List[A], lb: List[B])(f: (A, B) => C): List[C] =
apply(lb)(apply(la)(unit(f.curried)))
def map[A, B](la: List[A])(f: A => B): List[B] =
apply(la)(unit(f))
def fold[A](l: List[A])(z: A)(op: (A, A) ⇒ A): A =
foldRight(l, z)(op)
def filter[A](l: List[A])(f: A => Boolean): List[A] =
foldRight(l, Nil:List[A])((h,t) => if (f(h)) Cons(h,t) else t)

What are they
You can see, except for
unit[A](a: A): List[A]
fold[A](l: List[A])(z: A)(op: (A, A) ⇒ A): A
filter[A](l: List[A])(f: A => Boolean): List[A]
There are 3 groups:
1. flatMap/join/compose
2. apply/map2
3. map
inside each group, the methods are equivalent to each other. G1 => G2 => G3,
which means G1 can implement G2, G2 can implement G3.
Powerful G1 > G2 > G3 Generality G1 < G2 < G3
OO sense, G1 inherit from G2 inherit from G3

What are they
G1 is Monad Signature
G2 is Applicative Signature
G3 is Functor Signature
fold is the signature of Foldable
Monad with filter is called Zero Monad
It is easier to see, but much harder to understand.
What they are. Why we use them. What can they do.
Once you understand, you lost the ability to say it :)
We will find out that through our journey. Here we can have a small taste first.

Scala for comprehension
Any type that has
flatMap/map/filter defined on them can use for
comprehension.
Let us put those in OO/FP hybrid style

for comprehension
Use the OO/FP hybrid style code
we can do
def test = {
val a = List(1,2)
val b = List(3,4)
for {
t1 <- a
t2 <- b
} yield ((t1,t2))
}
We get
[ (1,3) (1,4) (2,3) (2,4) ]

for comprehension
It is in fact flatMap/map in disguise, it is same as
def test = {
val a = List(1,2)
val b = List(3,4)
a.flatMap {
t1 => b.map {
t2 => (t1,t2)
}
}
}
basically multiple List can combine together in any ways, without knowing what
inside, the last one is map, all the other are flatMap, you can also use if here in
for comprehension, which translate into filter

Fp in scala part 1

More Related Content

What's hot

Similar to Fp in scala part 1

Recently uploaded

Fp in scala part 1