The document discusses functional programming concepts in Scala, focusing on strictness and laziness in data structures and streams. It highlights the differences between strict and lazy evaluation using code examples, outlining the construction and use of streams and their transformations. Additionally, it delves into the implementation of fold operations for lists and streams, illustrating how they work in both strict and lazy contexts.













![List: A “Strict” Data Type
(1 to 10).toList map { i =>
println(s”list -> map $i”)
i + 10
} filter { i =>
println(s”list -> filter $i”)
i % 2 == 0
}
[1, 2, ... 10]
toList](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-14-2048.jpg)
![List: A “Strict” Data Type
(1 to 10).toList map { i =>
println(s”list -> map $i”)
i + 10
} filter { i =>
println(s”list -> filter $i”)
i % 2 == 0
}
[1, 2, ... 10]
Map [11, 12, ... 20]
toList
//
//
//
//
//
list
list
...
list
list
-> map 1
-> map 2
-> map 9
-> map 10](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-15-2048.jpg)
![List: A “Strict” Data Type
(1 to 10).toList map { i =>
println(s”list -> map $i”)
i + 10
} filter { i =>
println(s”list -> filter $i”)
i % 2 == 0
}
[1, 2, ... 10]
Map [11, 12, ... 20]
Filter
toList
[12, 14, ... 20]
//
//
//
//
//
//
//
//
//
//
list
list
...
list
list
list
list
...
list
list
-> map 1
-> map 2
->
->
->
->
map 9
map 10
10
filter 11
filter 12
-> filter 19
-> filter 20](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-16-2048.jpg)


![ams: Lazy Ass Seqs
Stre
Stream(1 to 10) map { i =>
println(s”stream -> map $i”)
i + 10
} filter { i =>
println(s”stream -> filter $i”)
i % 2 == 0
}
[1, ?]
Stream(1 to 10)](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-19-2048.jpg)
![ams: Lazy Ass Seqs
Stre
Stream(1 to 10) map { i =>
println(s”stream -> map $i”)
i + 10
} filter { i =>
println(s”stream -> filter $i”)
i % 2 == 0
}
[1, ?]
[11, ?]
Stream(1 to 10)
Map](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-20-2048.jpg)
![ams: Lazy Ass Seqs
Stre
Stream(1 to 10) map { i =>
println(s”stream -> map $i”)
i + 10
} filter { i =>
println(s”stream -> filter $i”)
i % 2 == 0
}
[1, ?]
[11, ?]
Stream(1 to 10)
Map
[12, ?]
Filter
The ?‘s are, essentially
functions](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-21-2048.jpg)
![ams: Lazy Ass Seqs
Stre
Stream(1 to 10) map { i =>
println(s”stream -> map $i”)
i + 10
} filter { i =>
println(s”stream -> filter $i”)
i % 2 == 0
}
[1, ?]
[11, ?]
Stream(1 to 10)
Map
[12, ?]
Filter
The ?‘s are, essentially
functions
ative purposes only
For il ustr](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-22-2048.jpg)
![ams: Lazy Ass Seqs
Stre
Stream(1 to 10) map { i =>
println(s”stream -> map $i”)
i + 10
} filter { i =>
println(s”stream -> filter $i”)
i % 2 == 0
}
[1, ?]
[11, ?]
Stream(1 to 10)
Map
[12, ?]
Filter
The ?‘s are, essentially
functions
ative purposes only
For il ustr
Stream transformation does not require traversal](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-23-2048.jpg)
![ams: Lazy Ass Seqs
Stre
Stream(1 to 10) map { i =>
println(s”stream -> map $i”)
i + 10
} filter { i =>
println(s”stream -> filter $i”)
i % 2 == 0
}
[1, ?]
[11, ?]
Stream(1 to 10)
Map
[12, ?]
Filter
The ?‘s are, essentially
functions
ative purposes only
For il ustr
Stream transformation does not require traversal
Transformations are applied on-demand as
traversal happens](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-24-2048.jpg)

![Stream Definition
trait Stream[+A] {
def uncons: Option[(A, Stream[A])]
}](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-26-2048.jpg)
![Stream Definition
trait Stream[+A] {
def uncons: Option[(A, Stream[A])]
}
The “data” structure](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-27-2048.jpg)
![Stream Definition
trait Stream[+A] {
def uncons: Option[(A, Stream[A])]
}
The “data” structure
Constructors
object Stream {
def empty[A]: Stream[A] = new Stream[A] {
def uncons = None
}
def cons[A](hd: => A, tl: => Stream[A]): Stream[A] = new Stream[A] {
def uncons = Some((hd, tl))
}
}](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-28-2048.jpg)
![Stream Definition
trait Stream[+A] {
def uncons: Option[(A, Stream[A])]
}
The “data” structure
Constructors
object Stream {
def empty[A]: Stream[A] = new Stream[A] {
def uncons = None
}
def cons[A](hd: => A, tl: => Stream[A]): Stream[A] = new Stream[A] {
def uncons = Some((hd, tl))
}
}](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-29-2048.jpg)

![Constructing Streams
val streamOfOne = cons(1, empty[Int])
val streamOfThree = cons(1, cons(2, cons(3, empty[Int])))](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-31-2048.jpg)
![Constructing Streams
val streamOfOne = cons(1, empty[Int])
val streamOfThree = cons(1, cons(2, cons(3, empty[Int])))
Well, that
SUCKS...](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-32-2048.jpg)
![Constructing Streams
val streamOfOne = cons(1, empty[Int])
val streamOfThree = cons(1, cons(2, cons(3, empty[Int])))
Well, that
SUCKS...
object Stream {
def apply[A](as: A*): Stream[A] = {
if (as.isEmpty) empty[A]
else cons(as.head, apply(as.tail:_*))
}
}](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-33-2048.jpg)
![Constructing Streams
val streamOfOne = cons(1, empty[Int])
val streamOfThree = cons(1, cons(2, cons(3, empty[Int])))
Well, that
SUCKS...
val three = Stream(1, 2, 3)
object Stream {
def apply[A](as: A*): Stream[A] = {
if (as.isEmpty) empty[A]
else cons(as.head, apply(as.tail:_*))
}
}](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-34-2048.jpg)

![The Stream... so far
trait Stream[+A] {
def uncons: Option[(A, Stream[A])]
}
!
object Stream {
def empty[A]: Stream[A] = new Stream[A] {
def uncons = None
}
def cons[A](hd: => A, tl: => Stream[A]): Stream[A] = new Stream[A] {
def uncons = Some((hd, tl))
}
def apply[A](as: A*): Stream[A] = {
if (as.isEmpty) empty[A]
else cons(as.head, apply(as.tail:_*))
}
}](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-36-2048.jpg)





 {
def foldRight[B](z: B)(f: (A, B) => B): B =
if (this.isEmpty) z
else f(head, tail.foldRight(z)(f))
}](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-42-2048.jpg)
 {
def foldRight[B](z: B)(f: (A, B) => B): B =
if (this.isEmpty) z
else f(head, tail.foldRight(z)(f))
}
val sum
// f(1,
// f(1,
// f(1,
// f(1,
// f(1,
// f(1,
// f(1,
// 10
= (1 to 4).foldRight(0)(_ + _)
tail.foldRight...
f(2, tail.foldRight...
f(2, f(3, tail.foldRight...
f(2, f(3, f(4, 0))))
f(2, f(3, 4)))
f(2, 7))
9)](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-43-2048.jpg)
 {
def foldRight[B](z: B)(f: (A, B) => B): B =
if (this.isEmpty) z
else f(head, tail.foldRight(z)(f))
}
Here A and B are both
Ints but they need not
be. Note that full
recursive expansion takes
place at the call site.
val sum
// f(1,
// f(1,
// f(1,
// f(1,
// f(1,
// f(1,
// f(1,
// 10
= (1 to 4).foldRight(0)(_ + _)
tail.foldRight...
f(2, tail.foldRight...
f(2, f(3, tail.foldRight...
f(2, f(3, f(4, 0))))
f(2, f(3, 4)))
f(2, 7))
9)](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-44-2048.jpg)






![Building foldRight
trait Stream[+A] {
def foldRight[B](z: ? B)(f: (A, ? B) => B): B
}](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-51-2048.jpg)
![Building foldRight
trait Stream[+A]Stream[+A] {
trait {
def uncons: Option[(A, Stream[A])]
def foldRight[B](z: ? B)(f: (A, ? B) => B): B
!
}
def foldRight[B](z: => B)(f: (A, => B) => B): B = uncons match {
case None => z
case Some((hd, tl)) => f(hd, tl.foldRight(z)(f))
}
}](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-52-2048.jpg)
![Building foldRight
trait Stream[+A]Stream[+A] {
trait {
def uncons: Option[(A, Stream[A])]
def foldRight[B](z: ? B)(f: (A, ? B) => B): B
!
}
def foldRight[B](z: => B)(f: (A, => B) => B): B = uncons match {
case None => z
case Some((hd, tl)) => f(hd, tl.foldRight(z)(f))
}
}
A profound change!](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-53-2048.jpg)
![Building foldRight
trait Stream[+A]Stream[+A] {
trait {
def uncons: Option[(A, Stream[A])]
def foldRight[B](z: ? B)(f: (A, ? B) => B): B
!
}
def foldRight[B](z: => B)(f: (A, => B) => B): B = uncons match {
case None => z
case Some((hd, tl)) => f(hd, tl.foldRight(z)(f))
}
}
The recursive call is no longer evaluated at the call site
because ‘f’ receives it by name](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-54-2048.jpg)

(f: (A, => B) => B): B](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-56-2048.jpg)
(f: (A, => B) => B): B
At this point, you’re potentially confused](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-57-2048.jpg)
(f: (A, => B) => B): B
At this point, you’re potentially confused
What good is it to have a lazy => B when foldRight must return a strict B?](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-58-2048.jpg)
(f: (A, => B) => B): B
At this point, you’re potentially confused
What good is it to have a lazy => B when foldRight must return a strict B?
def sum(ints: Stream[Int]): Int = ints.foldRight(0)(_ + _)](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-59-2048.jpg)
(f: (A, => B) => B): B
At this point, you’re potentially confused
What good is it to have a lazy => B when foldRight must return a strict B?
def sum(ints: Stream[Int]): Int = ints.foldRight(0)(_ + _)
val neverGetsHere = sum(streamOfNaturalNumbers)](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-60-2048.jpg)
(f: (A, => B) => B): B
T
”
T
IC
TR
S
At this point, you’re potentially confused
“
a
s
What good is it to have a lazy => B when foldRight must return a strict B?
I
i
t
n
def sum(ints: Stream[Int]): Int = ints.foldRight(0)(_ + _)
val neverGetsHere = sum(streamOfNaturalNumbers)](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-61-2048.jpg)


![Learning to Relax
Ok, I kinda lied… it’s not that Int is a “strict type”
(You can, of course, do something useful with an Int… such as)
def sumToN(ints: Stream[Int], to: Int): Int =
ints.take(to).foldRight(0)(_ + _)](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-64-2048.jpg)
![Learning to Relax
Ok, I kinda lied… it’s not that Int is a “strict type”
(You can, of course, do something useful with an Int… such as)
def sumToN(ints: Stream[Int], to: Int): Int =
ints.take(to).foldRight(0)(_ + _)
It’s just that the strict type can cause a bit of confusion because of its
non-lazy nature.](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-65-2048.jpg)
![Learning to Relax
Ok, I kinda lied… it’s not that Int is a “strict type”
(You can, of course, do something useful with an Int… such as)
def sumToN(ints: Stream[Int], to: Int): Int =
ints.take(to).foldRight(0)(_ + _)
It’s just that the strict type can cause a bit of confusion because of its
non-lazy nature.
The more “interesting” stuff, though happens when you can continue
beings lazy and stay within the realm of the infinite](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-66-2048.jpg)

(f: (A, => B) => B): B](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-68-2048.jpg)
(f: (A, => B) => B): B
Switching to a lazy (by name) parameter gives ‘f’ control
over the recursion](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-69-2048.jpg)
(f: (A, => B) => B): B
Switching to a lazy (by name) parameter gives ‘f’ control
over the recursion
‘f’ can decide to delay the execution of its second parameter,
eliminating the recursive call, returning control to the caller](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-70-2048.jpg)
(f: (A, => B) => B): B
Switching to a lazy (by name) parameter gives ‘f’ control
over the recursion
‘f’ can decide to delay the execution of its second parameter,
eliminating the recursive call, returning control to the caller
However, you can’t just delay a computation without shoving
it into some sort of context...](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-71-2048.jpg)
(f: (A, => B) => B): B
Switching to a lazy (by name) parameter gives ‘f’ control
over the recursion
‘f’ can decide to delay the execution of its second parameter,
eliminating the recursive call, returning control to the caller
However, you can’t just delay a computation without shoving
it into some sort of context...](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-72-2048.jpg)


: Stream[T] =
foldRight(empty[T]) { (head, tail) =>
cons(f(head), tail)
}](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-75-2048.jpg)
: Stream[T] =
foldRight(empty[T]) { (head, tail) =>
cons(f(head), tail)
}
def foldRight[B](z: => B)(f: (A, => B) => B): B](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-76-2048.jpg)
: Stream[T] =
foldRight(empty[T]) { (head, tail) =>
cons(f(head), tail)
}
Stream!
St
r
ea
m
St
r
!
ea
m
m
!
!
def foldRight[B](z: => B)(f: (A, => B) => B): B](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-77-2048.jpg)

![Enter... Filter
def filter(p: A => Boolean): Stream[A] =
foldRight(empty[A]) { (head, tail) =>
if (p(head)) cons(head, tail)
else tail
}](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-79-2048.jpg)
![Enter... Filter
def filter(p: A => Boolean): Stream[A] =
foldRight(empty[A]) { (head, tail) =>
if (p(head)) cons(head, tail)
else tail
}
def foldRight[B](z: => B)(f: (A, => B) => B): B](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-80-2048.jpg)
![Enter... Filter
def filter(p: A => Boolean): Stream[A] =
foldRight(empty[A]) { (head, tail) =>
if (p(head)) cons(head, tail)
else tail
St
re
}
am
Stream!
!
St
r
ea
St
r
ea
m
m
!
def foldRight[B](z: => B)(f: (A, => B) => B): B
!](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-81-2048.jpg)





: Stream[T] =
foldRight(empty[T]) { (head, tail) =>](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-87-2048.jpg)
: Stream[T] =
foldRight(empty[T]) { (head, tail) =>
Not Eval’d](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-88-2048.jpg)
: Stream[T] =
foldRight(empty[T]) { (head, tail) =>
!
!
!
Not Eval’d
!
Not Eval’d
!
cons(f(head), tail)
}](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-89-2048.jpg)
: Stream[T] =
foldRight(empty[T]) { (head, tail) =>
!
!
!
Not Eval’d
Not Eval’d
!
Not Eval’d
!
cons(f(head), tail)
}](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-90-2048.jpg)
: Stream[T] =
foldRight(empty[T]) { (head, tail) =>
!
!
!
Not Eval’d
Not Eval’d
!
Not Eval’d
!
cons(f(head), tail)
}
Jeez, does
this code
even do
anything!?](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-91-2048.jpg)


: Stream[T] =
foldRight(empty[T]) { (head, tail) =>
cons(f(head), tail)
}
Remember
that...
and...
def foldRight[B](z: => B)(f: (A, => B) => B): B
def cons[A](hd: => A, tl: => Stream[A]): Stream[A]
and...](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-94-2048.jpg)


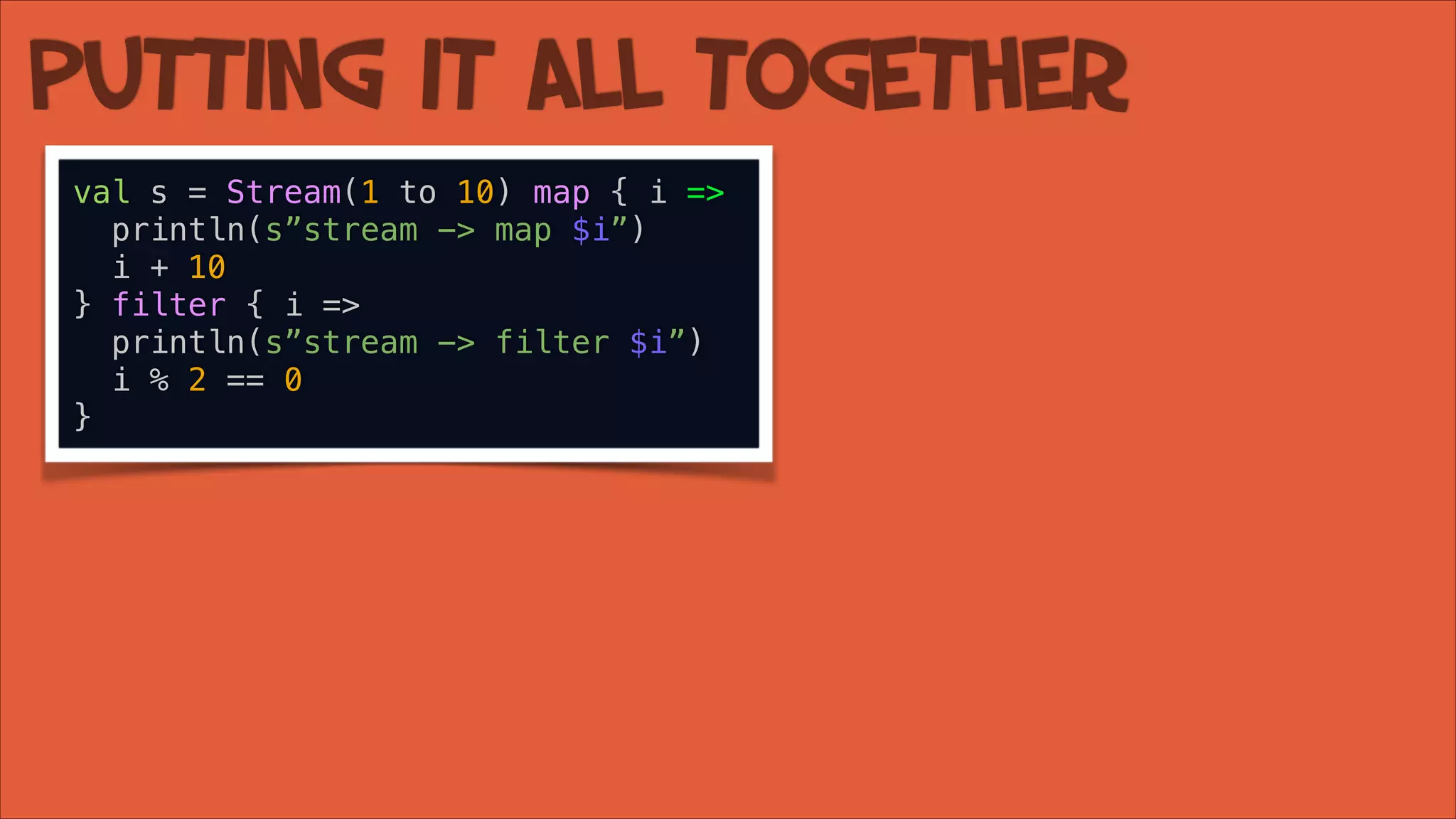

![Putting it All Together
val s = Stream(1 to 10) map { i =>
println(s”stream -> map $i”)
i + 10
} filter { i =>
println(s”stream -> filter $i”)
i % 2 == 0
}
def toList: List[A] = uncons match {
case None => Nil
case Some((h, t)) => h :: t.toList
}
Prints nothing.
OK
add toList()](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-99-2048.jpg)


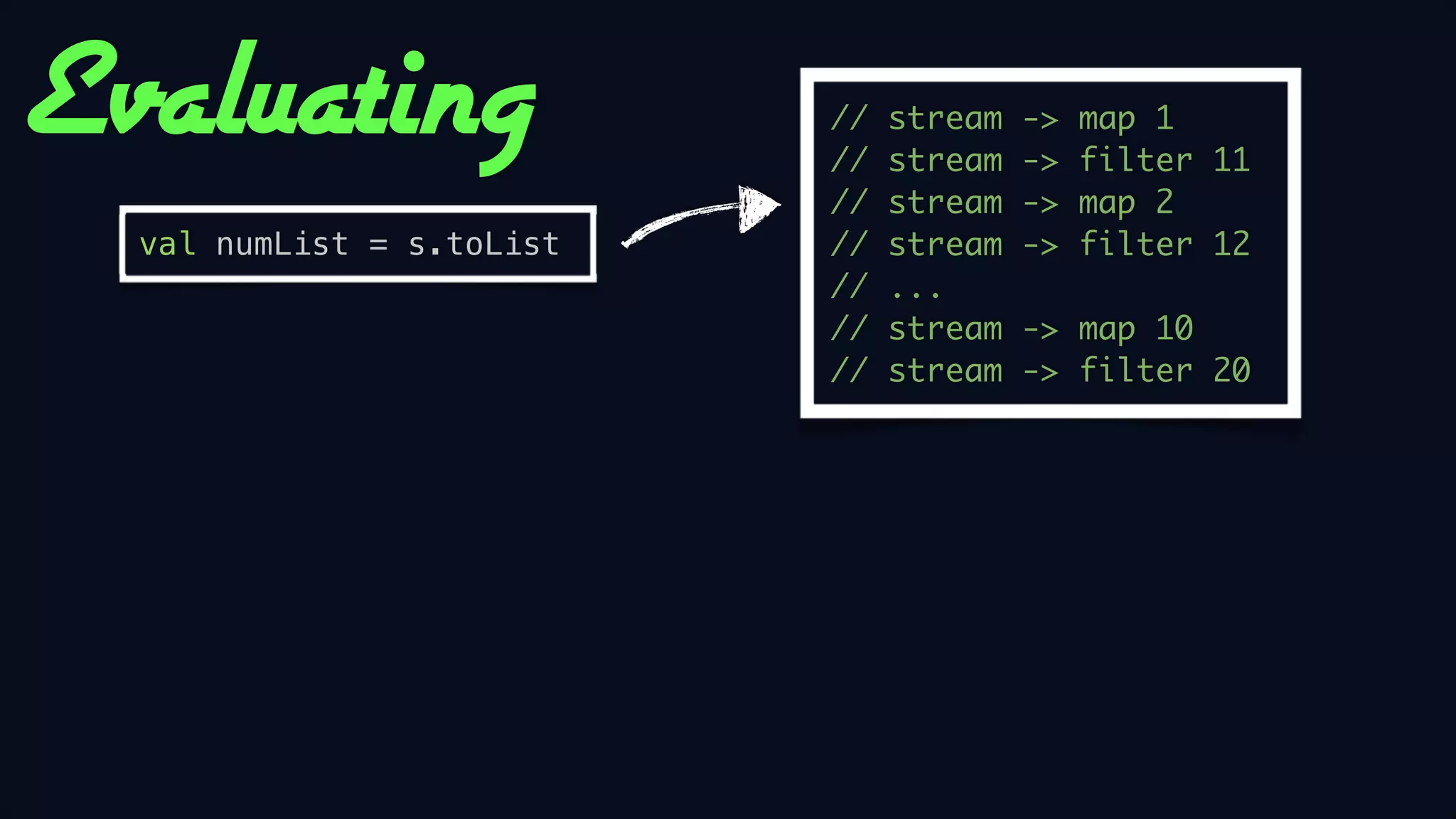
![Evaluating
val numList = s.toList
def take(n: Int): Stream[A] =
uncons match {
case Some((h, t)) if n > 0 =>
cons(h, t.take(n - 1))
case _ =>
empty
}
//
//
//
//
//
//
//
stream
stream
stream
stream
...
stream
stream
->
->
->
->
map 1
filter 11
map 2
filter 12
-> map 10
-> filter 20](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-103-2048.jpg)
![Evaluating
val numList = s.toList
def take(n: Int): Stream[A] =
uncons match {
case Some((h, t)) if n > 0 =>
cons(h, t.take(n - 1))
case _ =>
empty
}
val numList = s.take(1).toList
//
//
//
//
//
//
//
stream
stream
stream
stream
...
stream
stream
->
->
->
->
map 1
filter 11
map 2
filter 12
-> map 10
-> filter 20](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-104-2048.jpg)
![Evaluating
val numList = s.toList
def take(n: Int): Stream[A] =
uncons match {
case Some((h, t)) if n > 0 =>
cons(h, t.take(n - 1))
case _ =>
empty
}
val numList = s.take(1).toList
//
//
//
//
//
//
//
stream
stream
stream
stream
...
stream
stream
//
//
//
//
->
->
->
->
map 1
filter 11
map 2
filter 12
-> map 10
-> filter 20
stream
stream
stream
stream
->
->
->
->
map 1
filter 11
map 2
filter 12](https://image.slidesharecdn.com/functionalstreams-140216113247-phpapp02/75/Building-a-Functional-Stream-in-Scala-105-2048.jpg)






