Downloaded 336 times
![How?
Box et al. (1978) “There tends to be a redundancy in [full factorial designs]
– redundancy in terms of an excess number of
interactions that can be estimated …
Fractional factorial designs exploit this redundancy …” philosophy](https://image.slidesharecdn.com/ffd-tutorial-121223001122-phpapp01/85/Fractional-factorial-design-tutorial-26-320.jpg)
![How?
Box et al. (1978) “There tends to be a redundancy in [full factorial designs]
– redundancy in terms of an excess number of
interactions that can be estimated …
Fractional factorial designs exploit this redundancy …” philosophy](https://image.slidesharecdn.com/ffd-tutorial-121223001122-phpapp01/75/Fractional-factorial-design-tutorial-26-2048.jpg)
Uploaded byGaurav Kr
Fractional factorial design tutorial
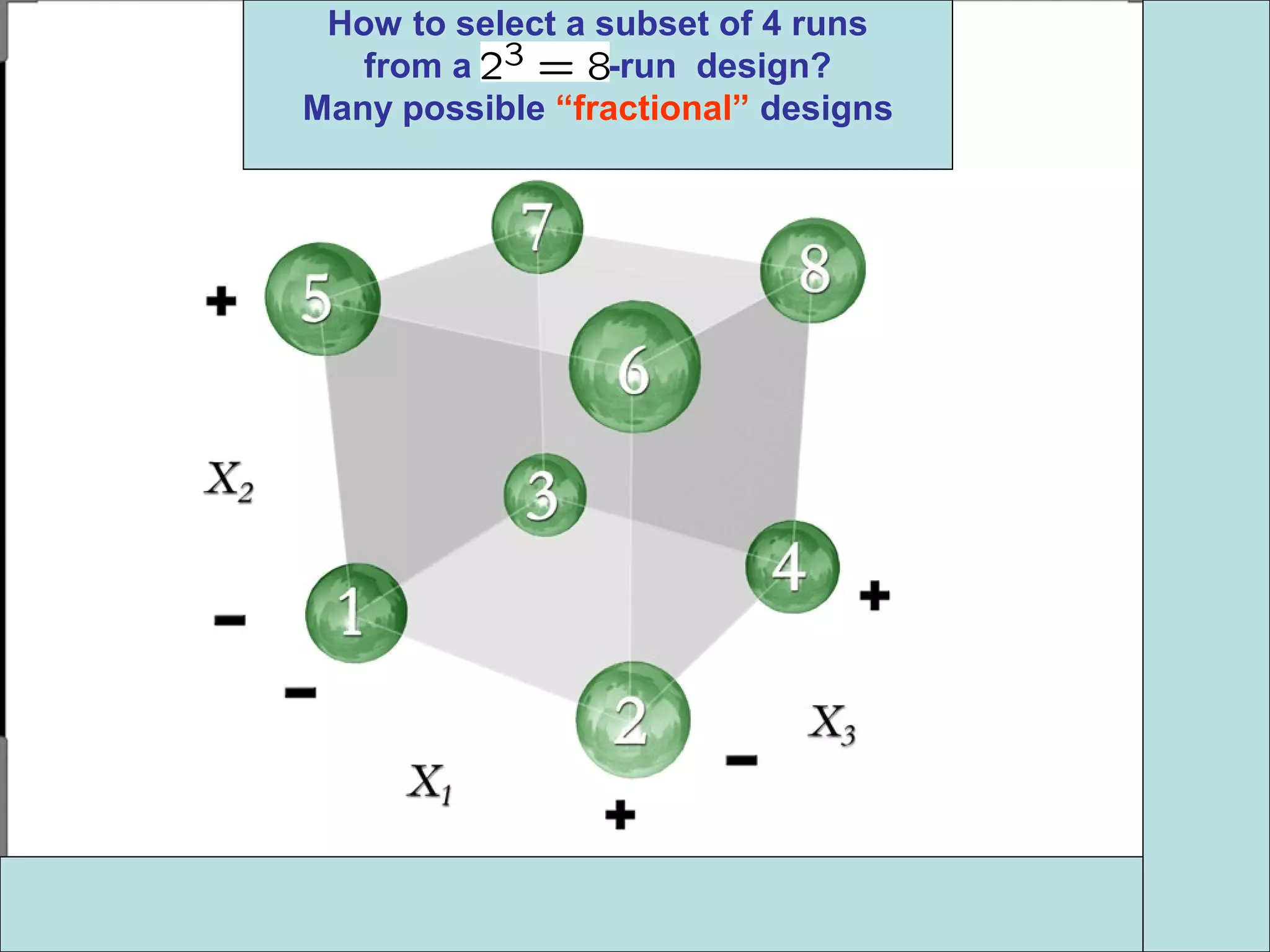
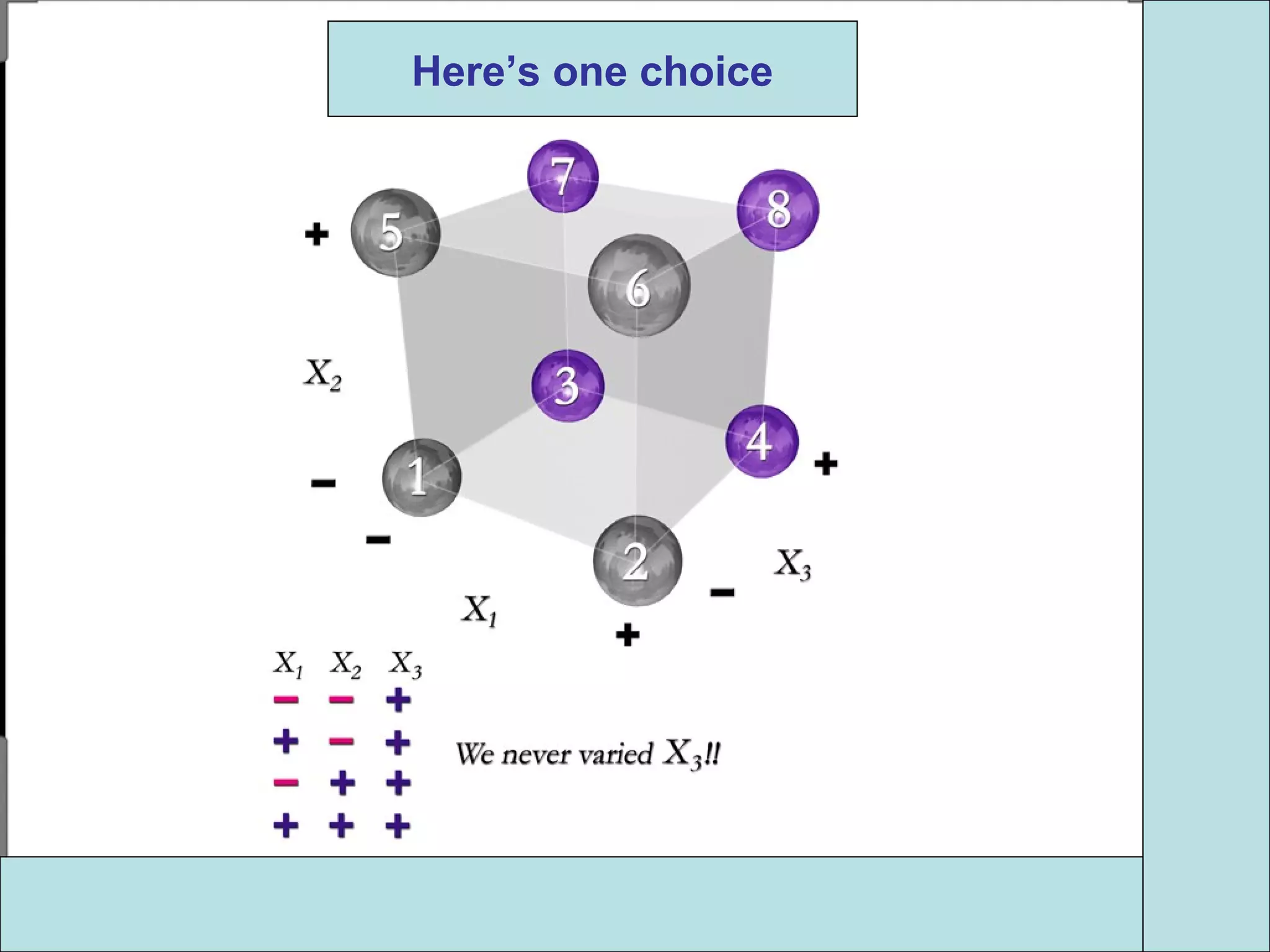
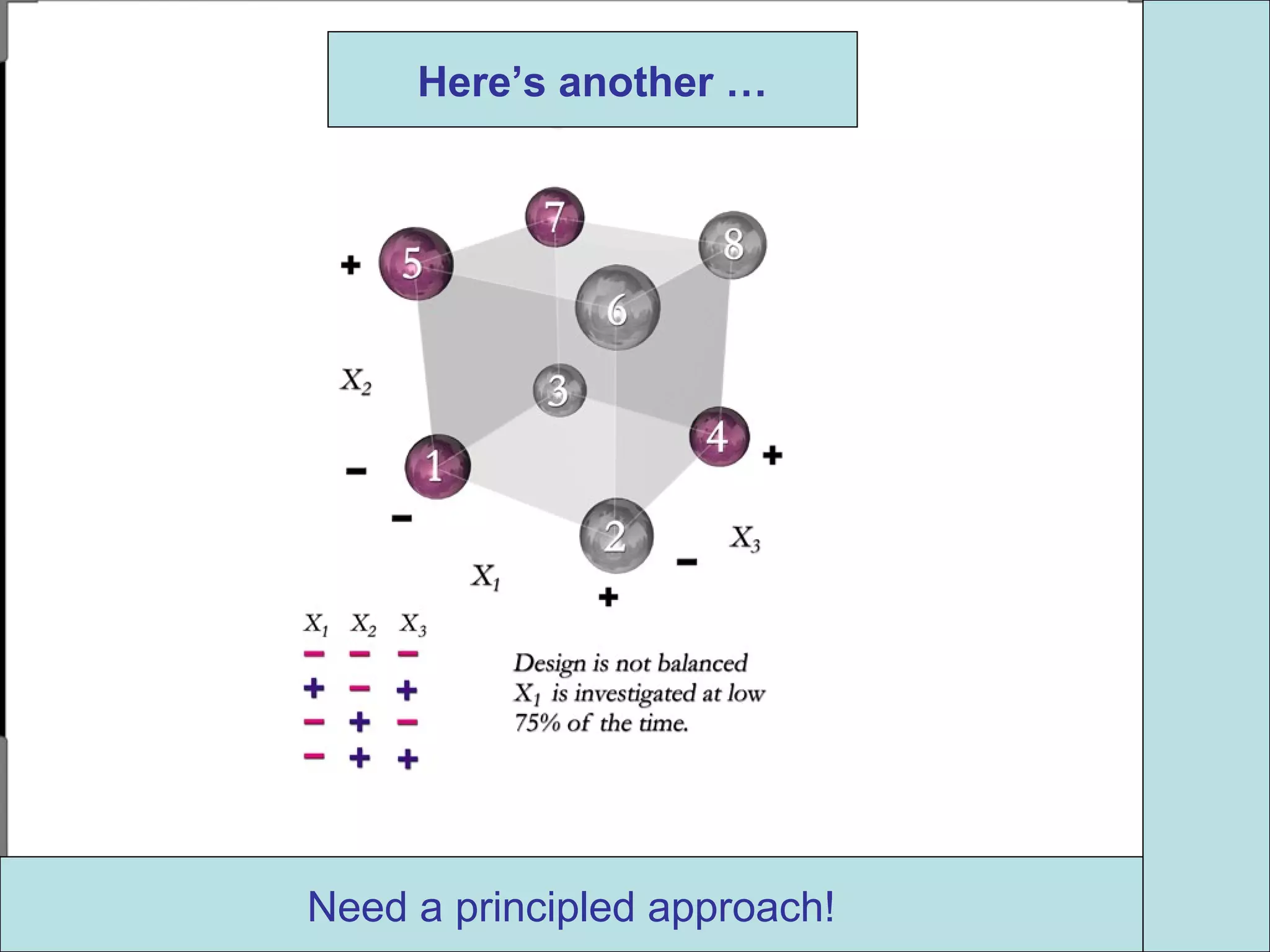
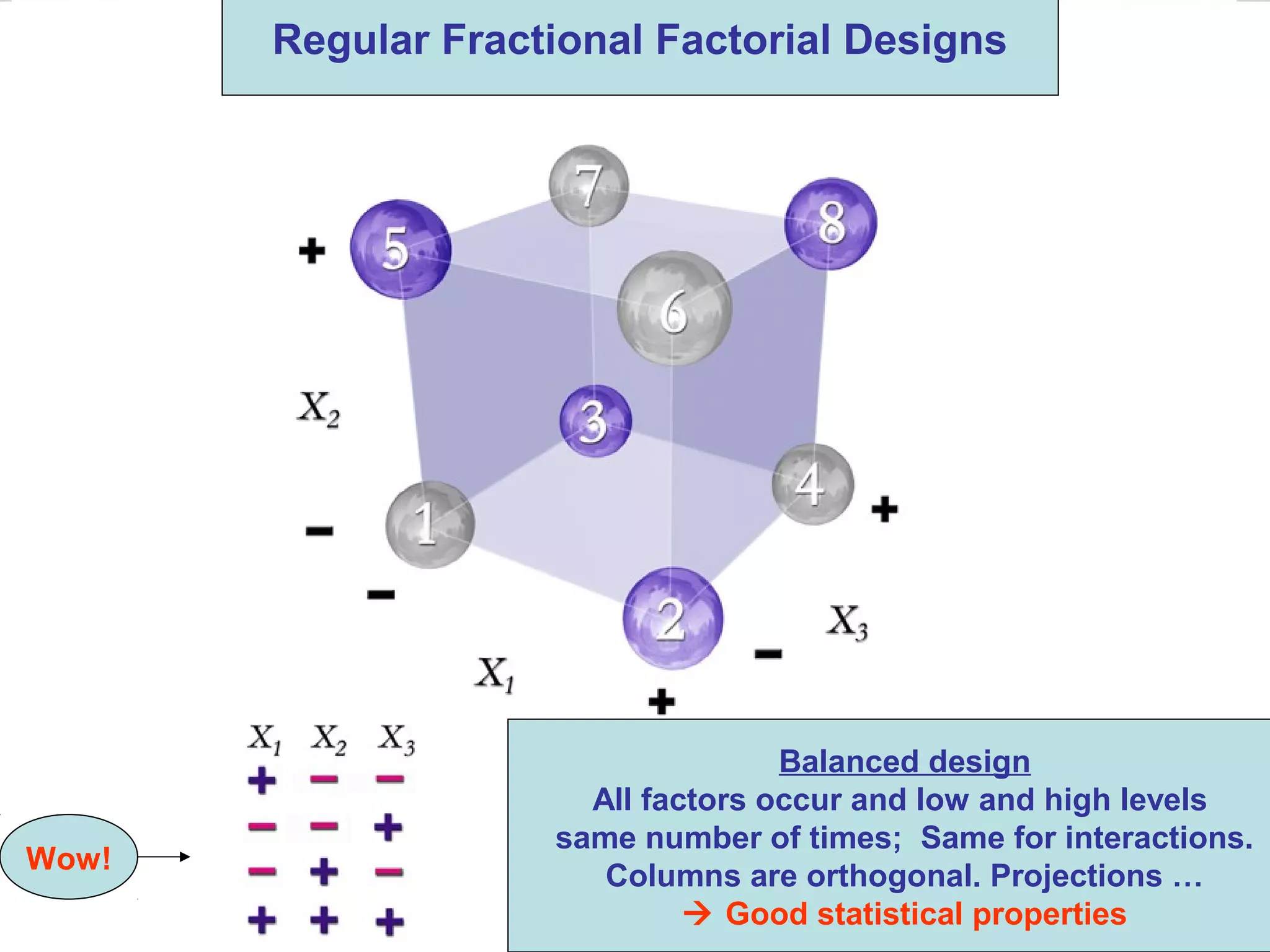
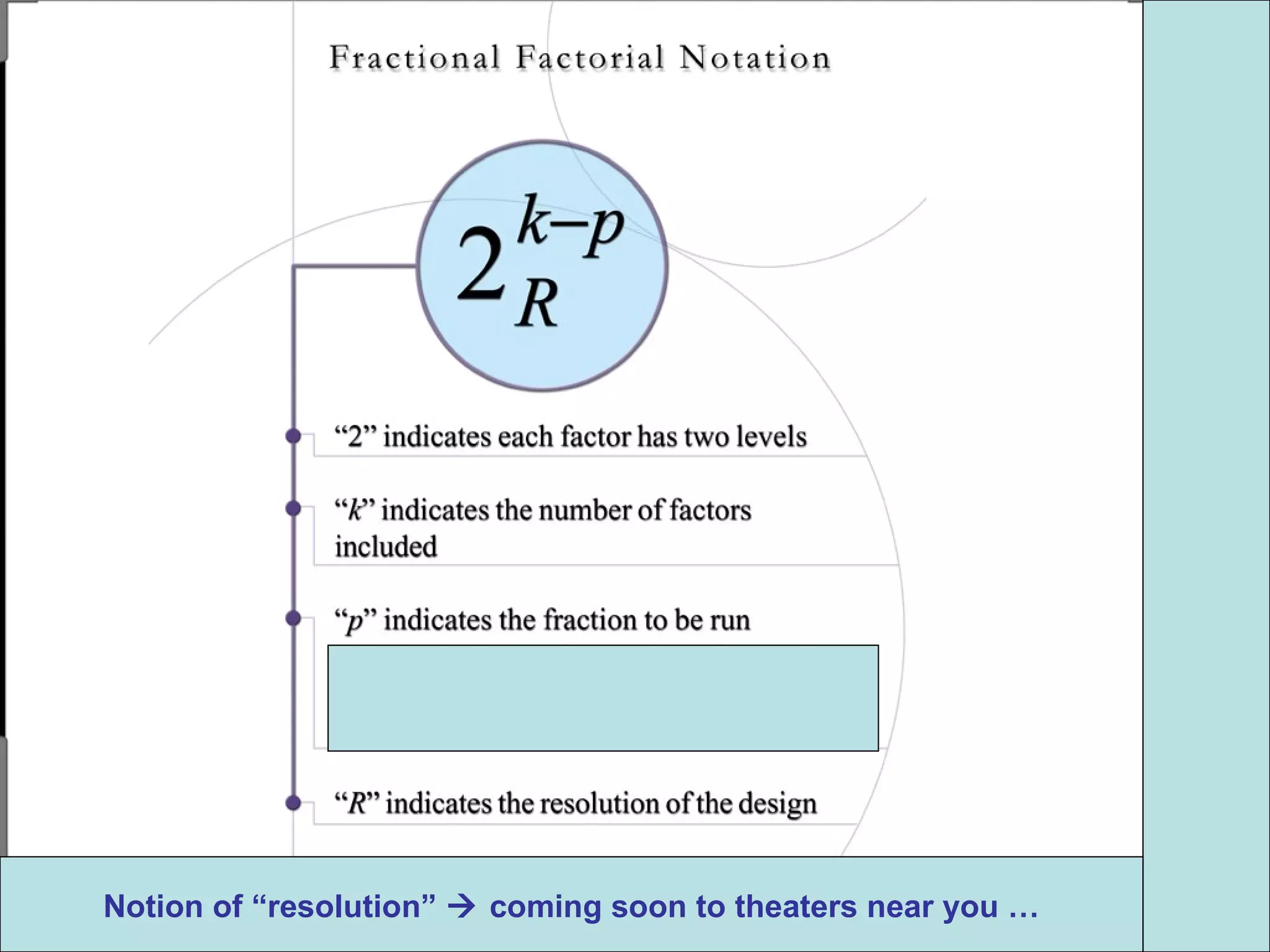
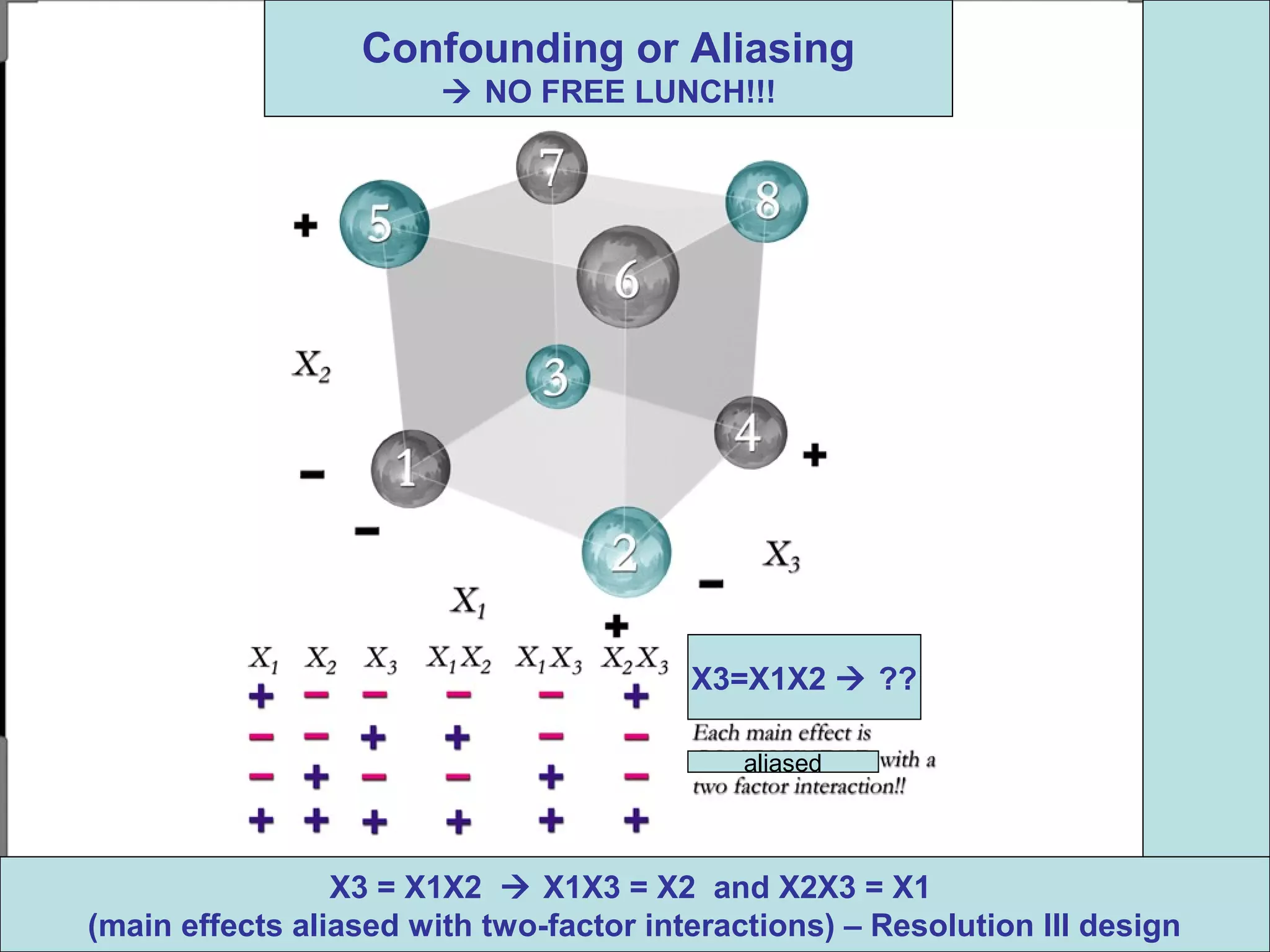
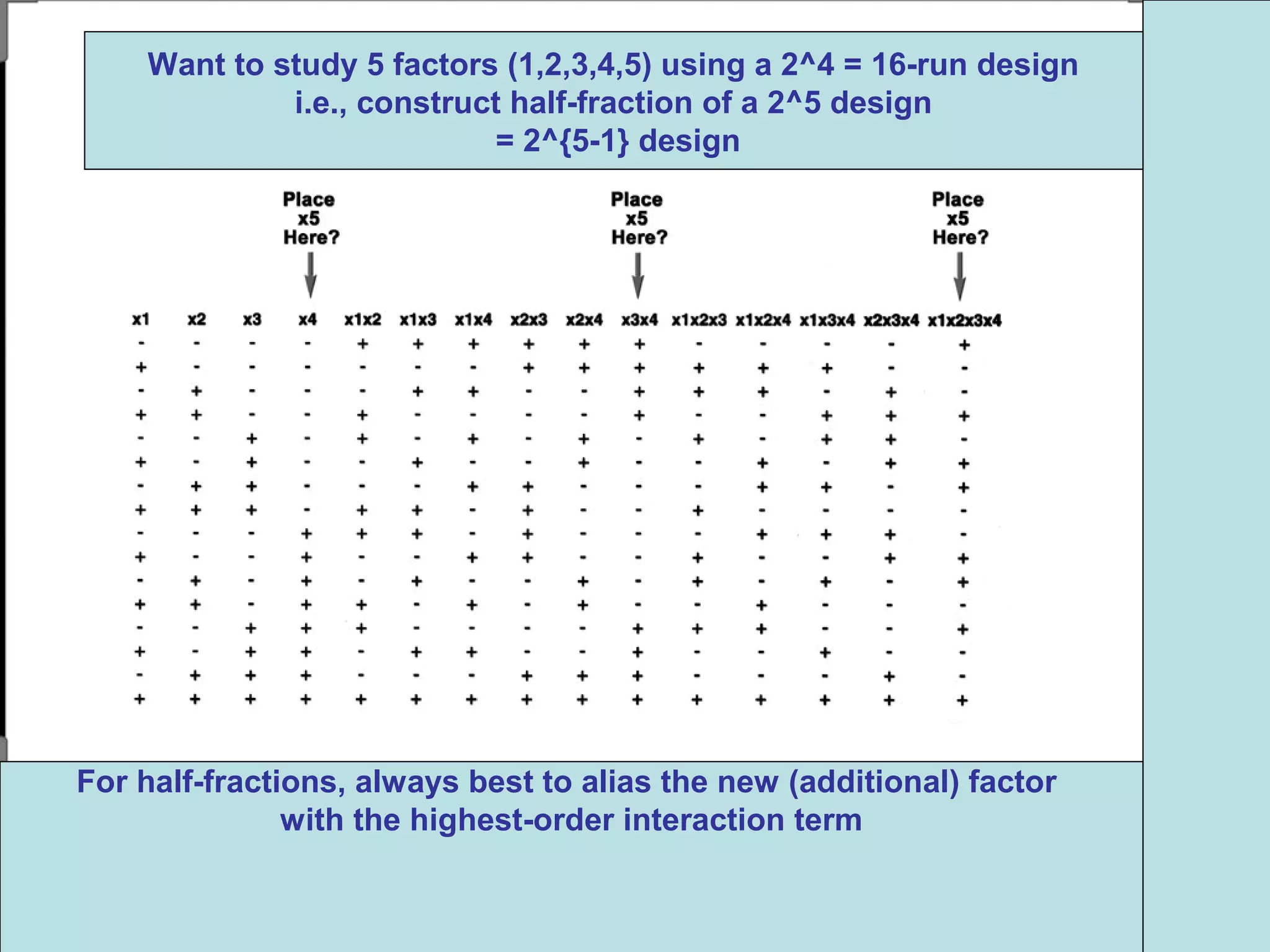
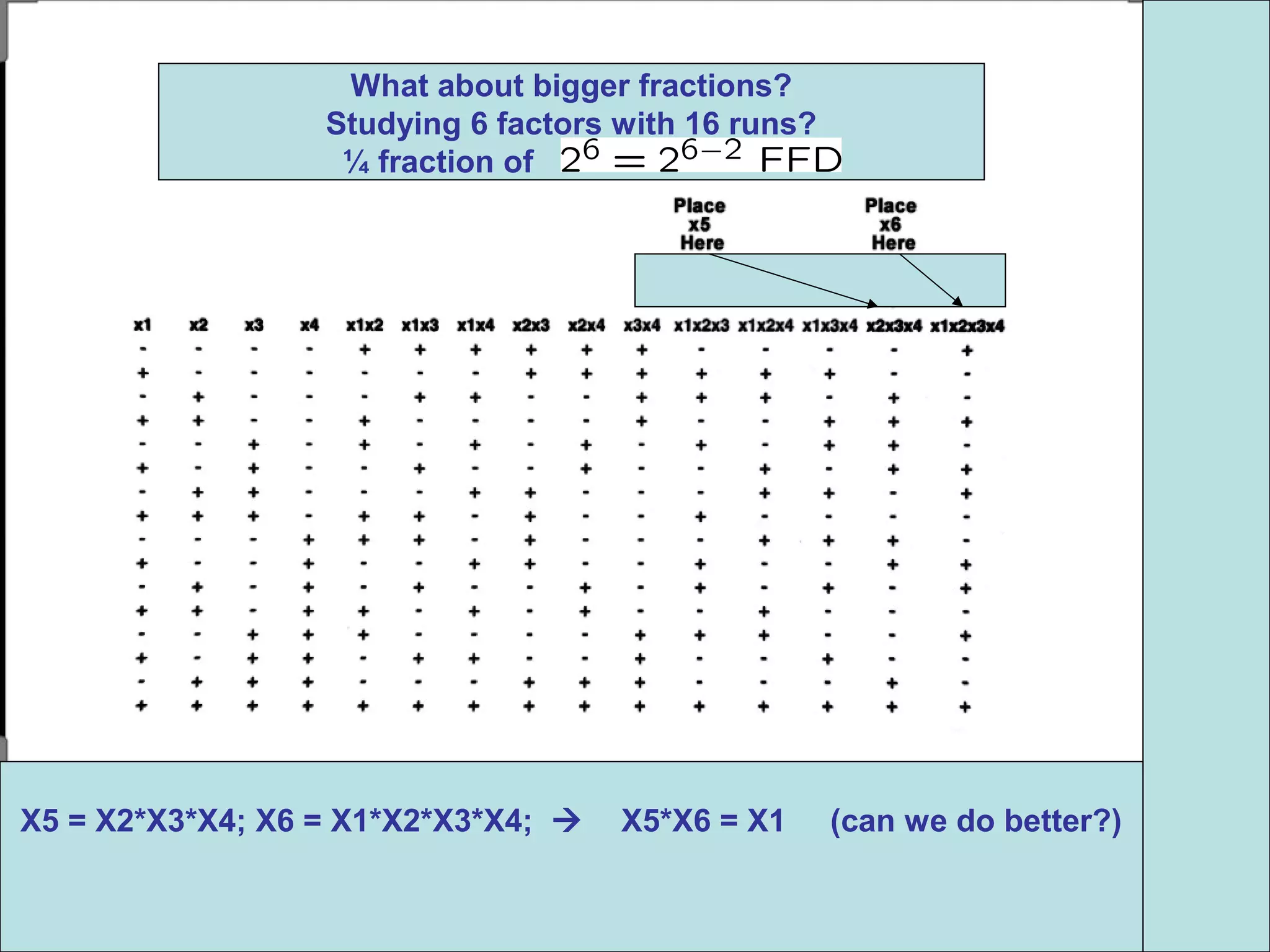
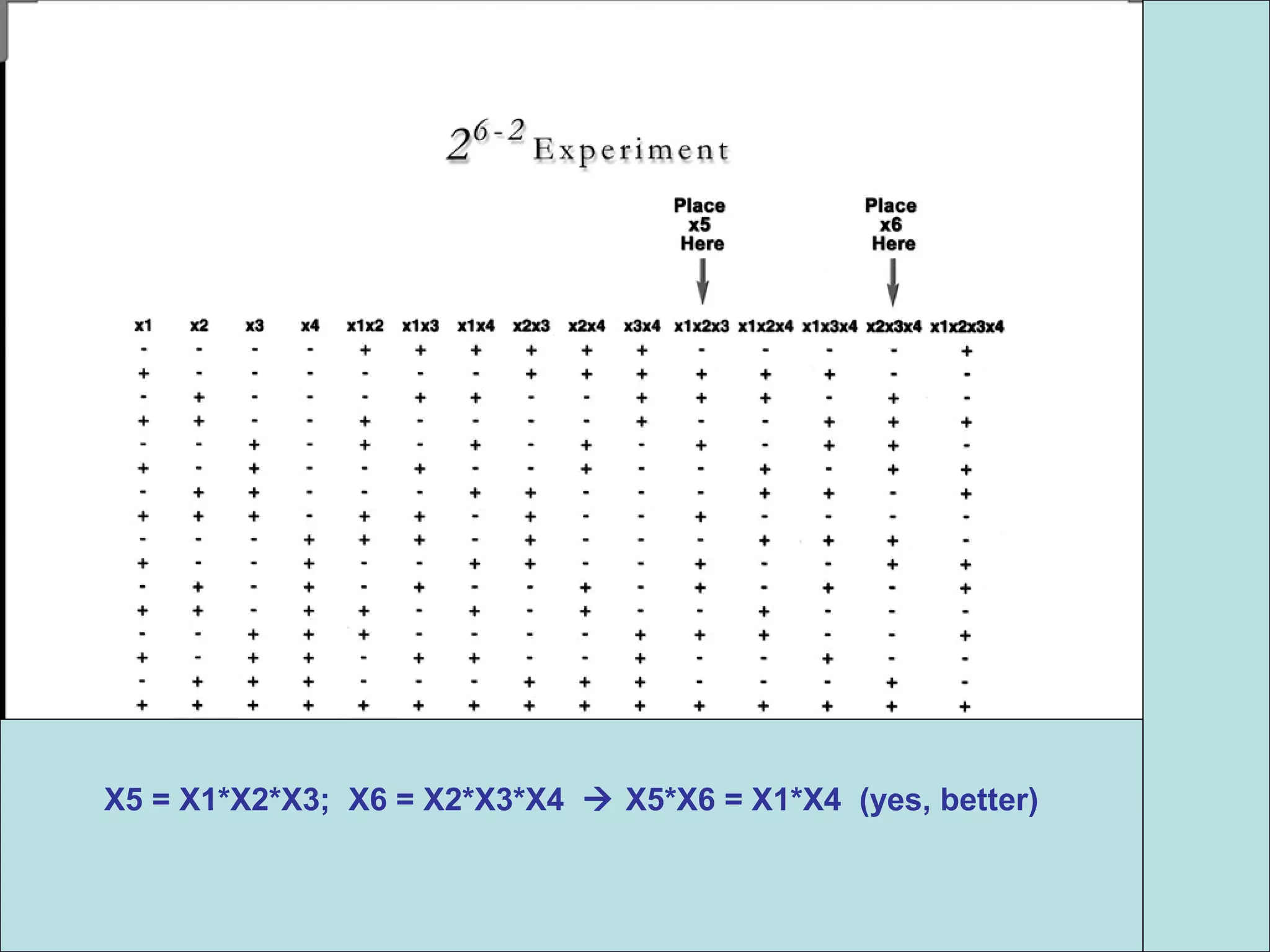
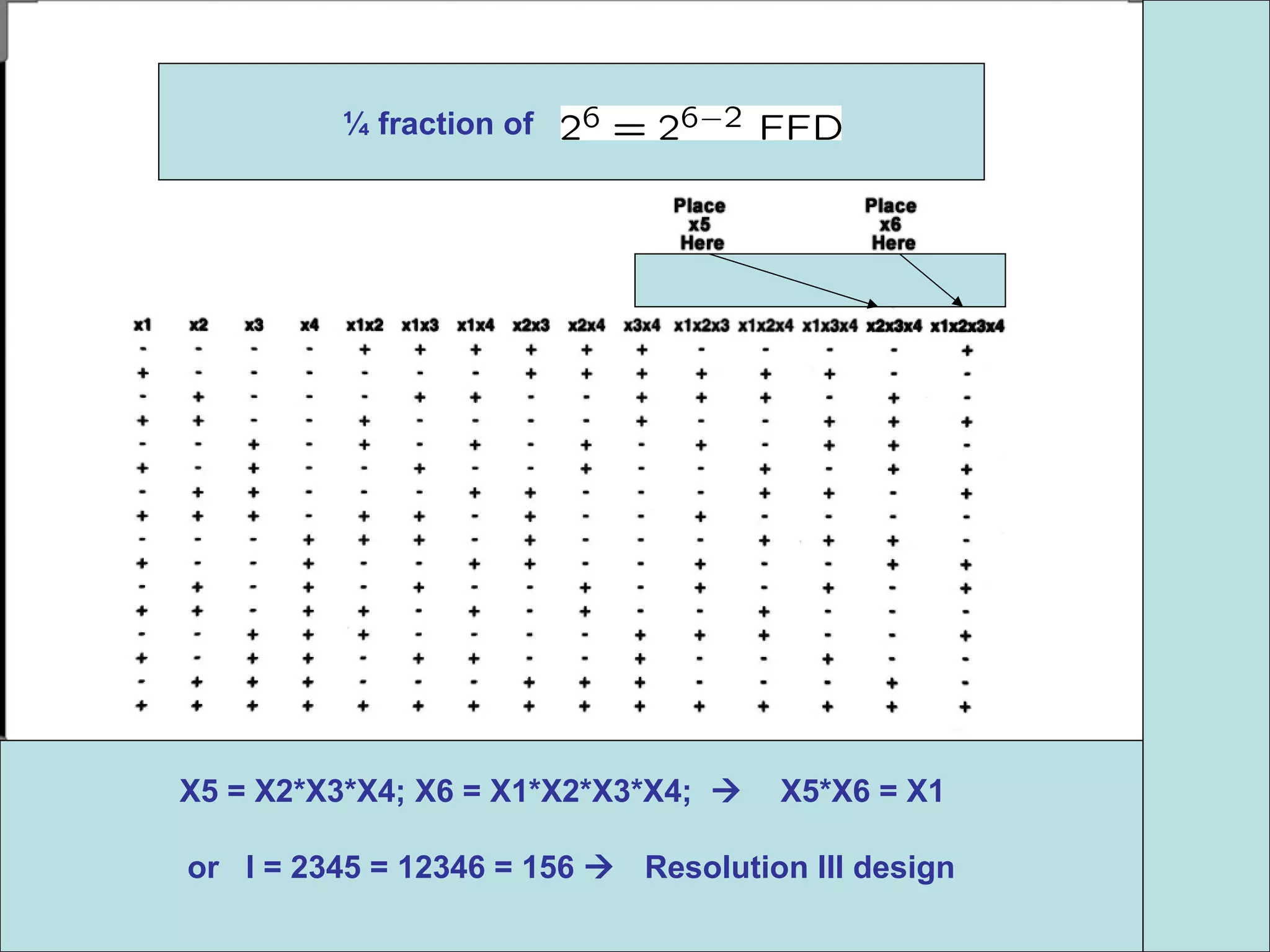
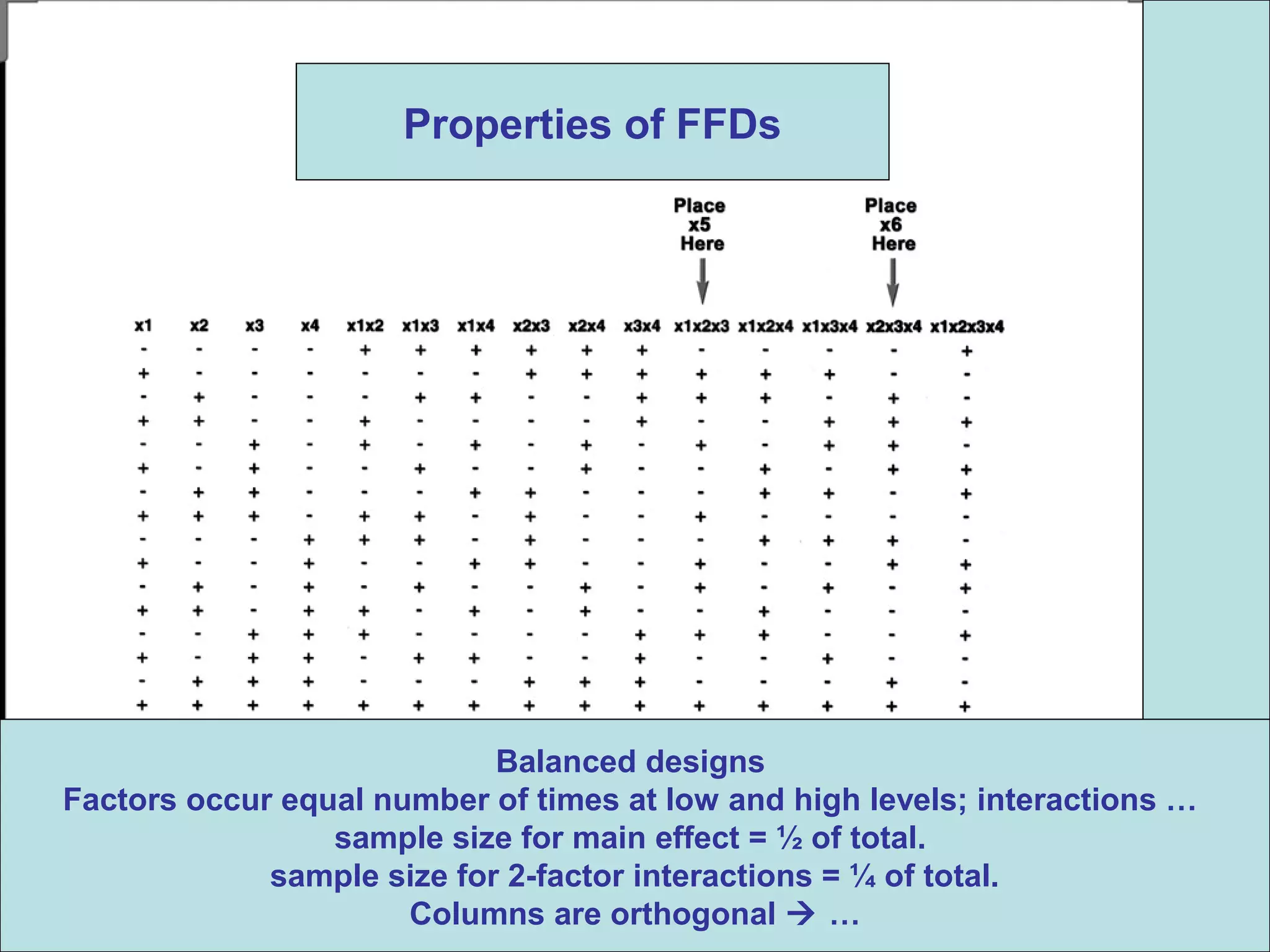
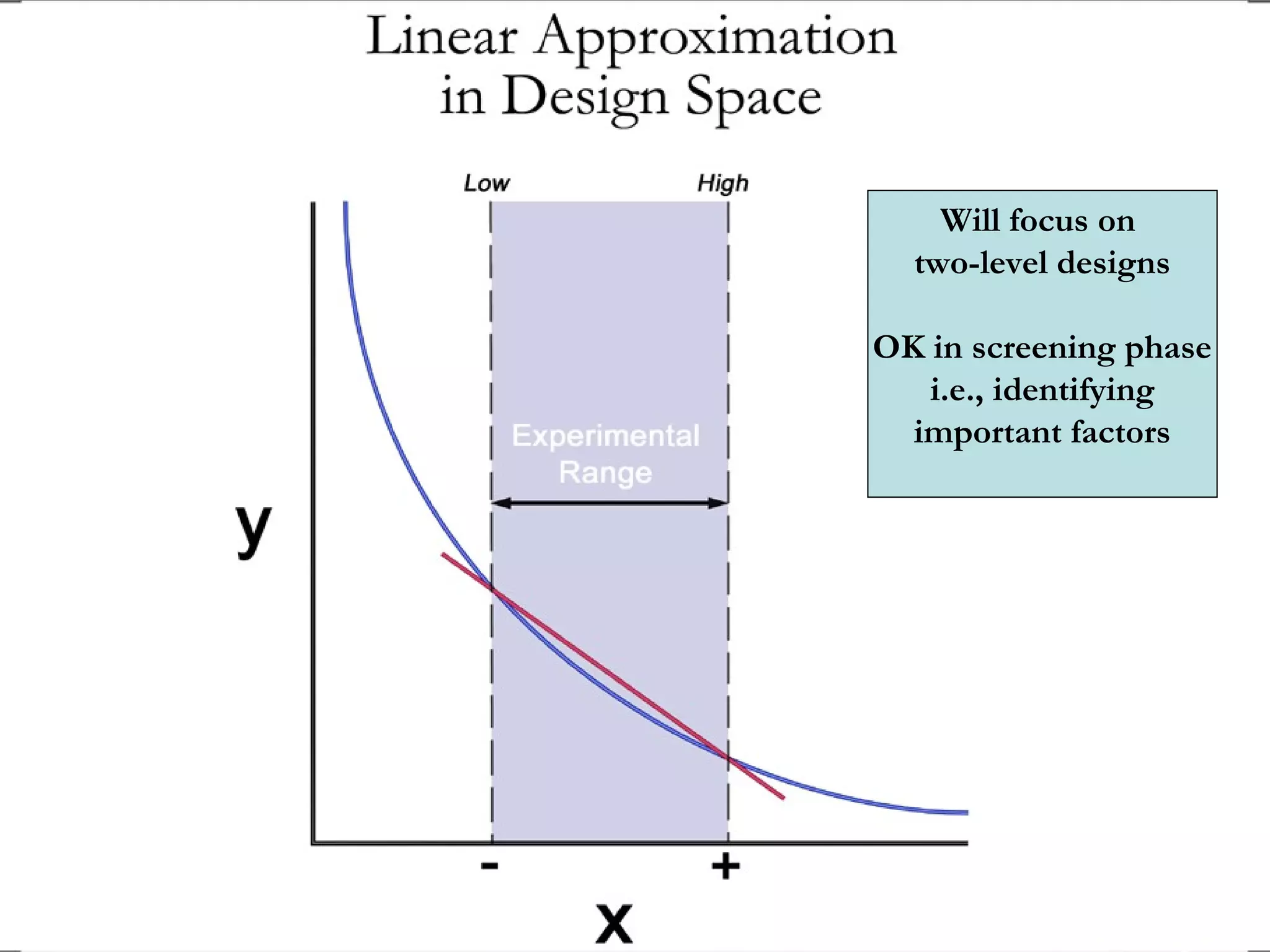
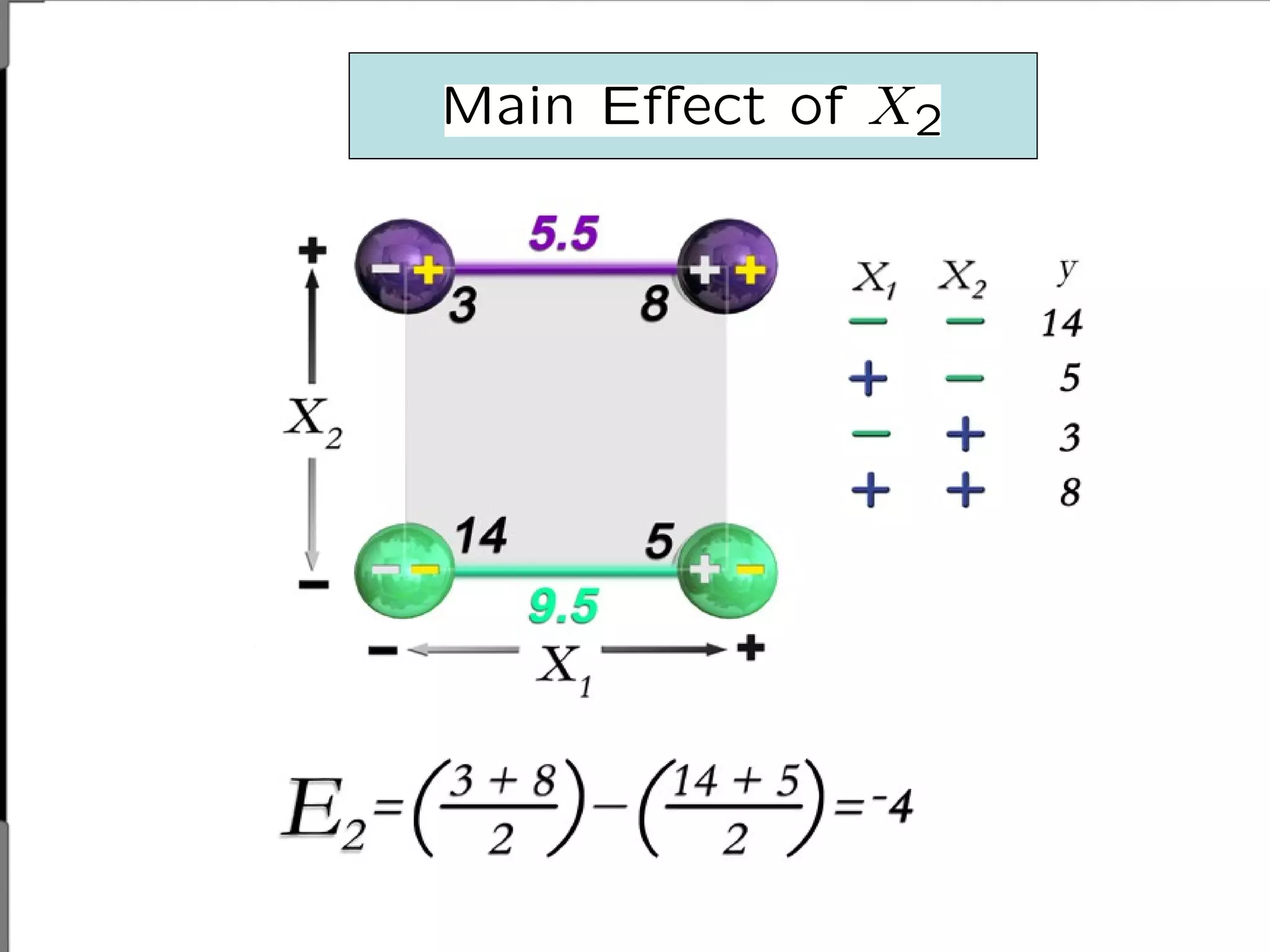
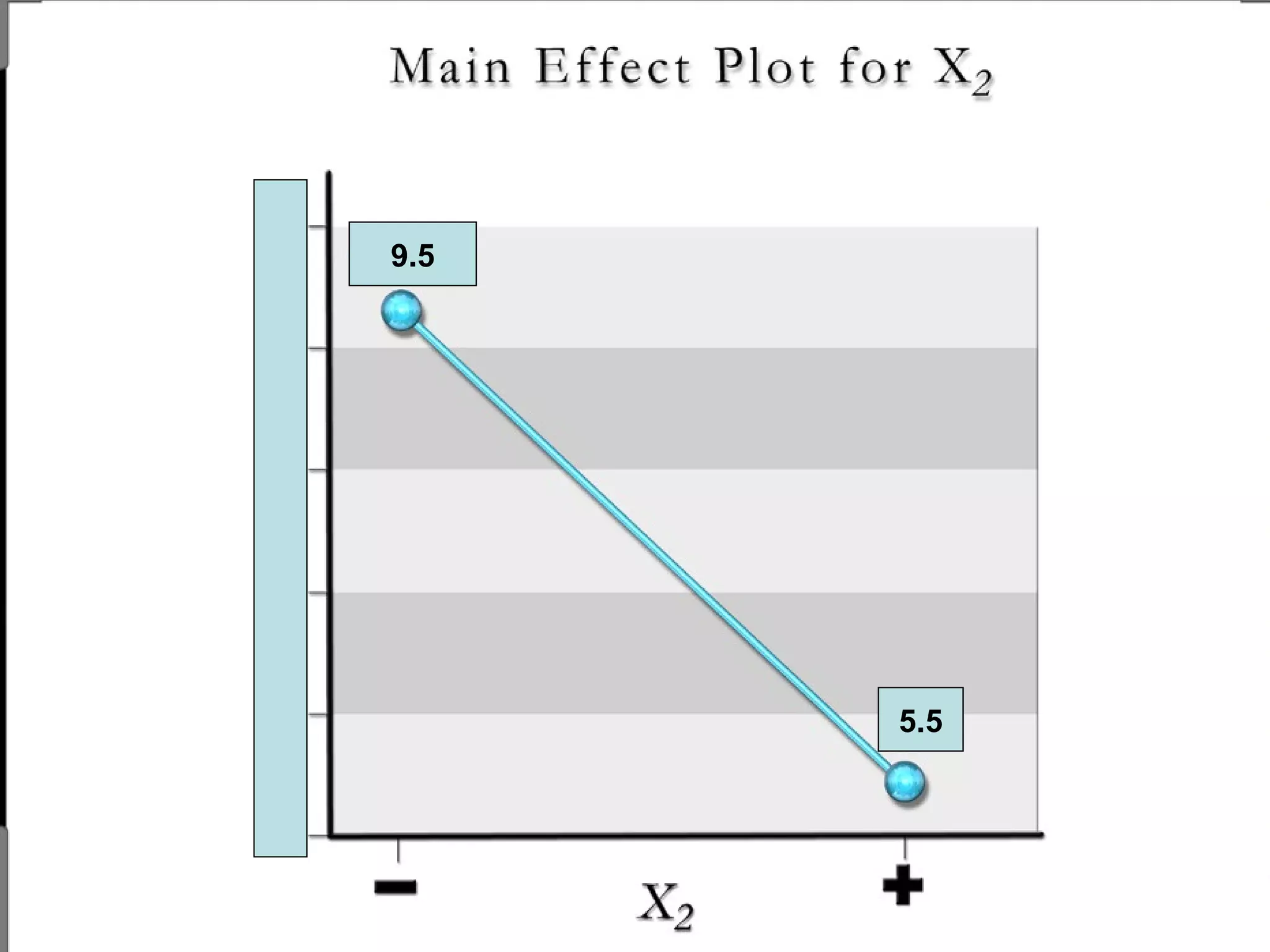
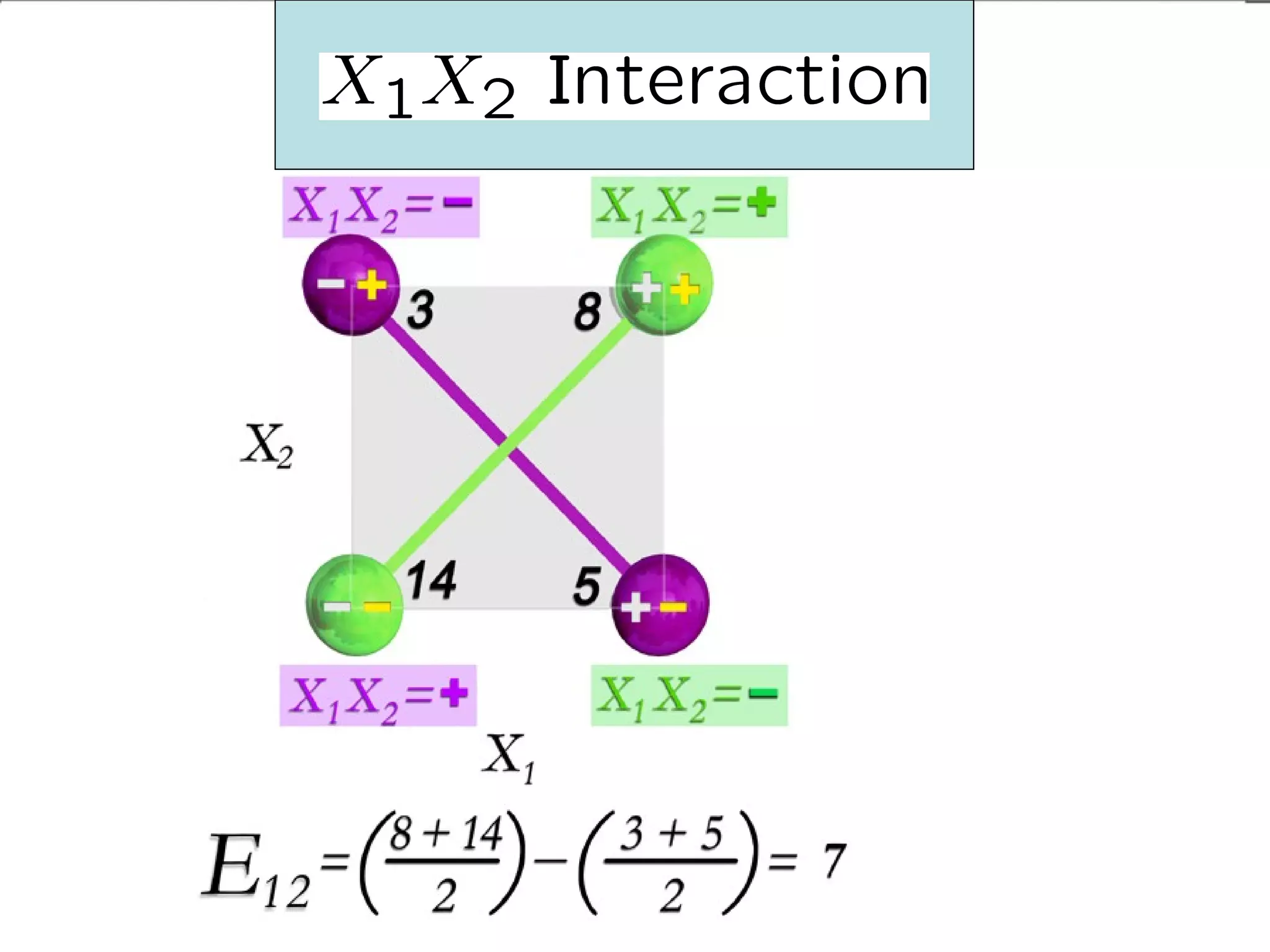
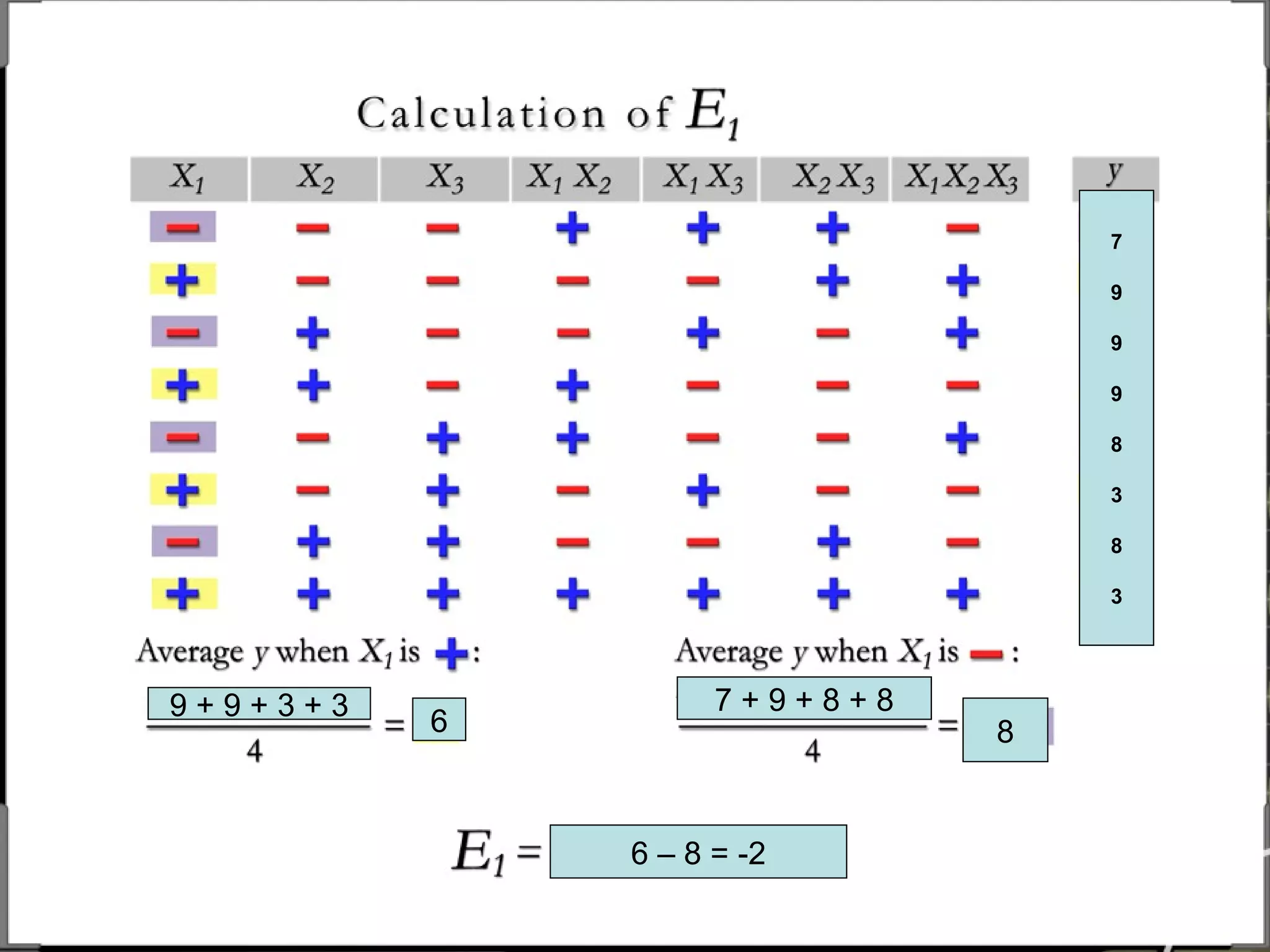
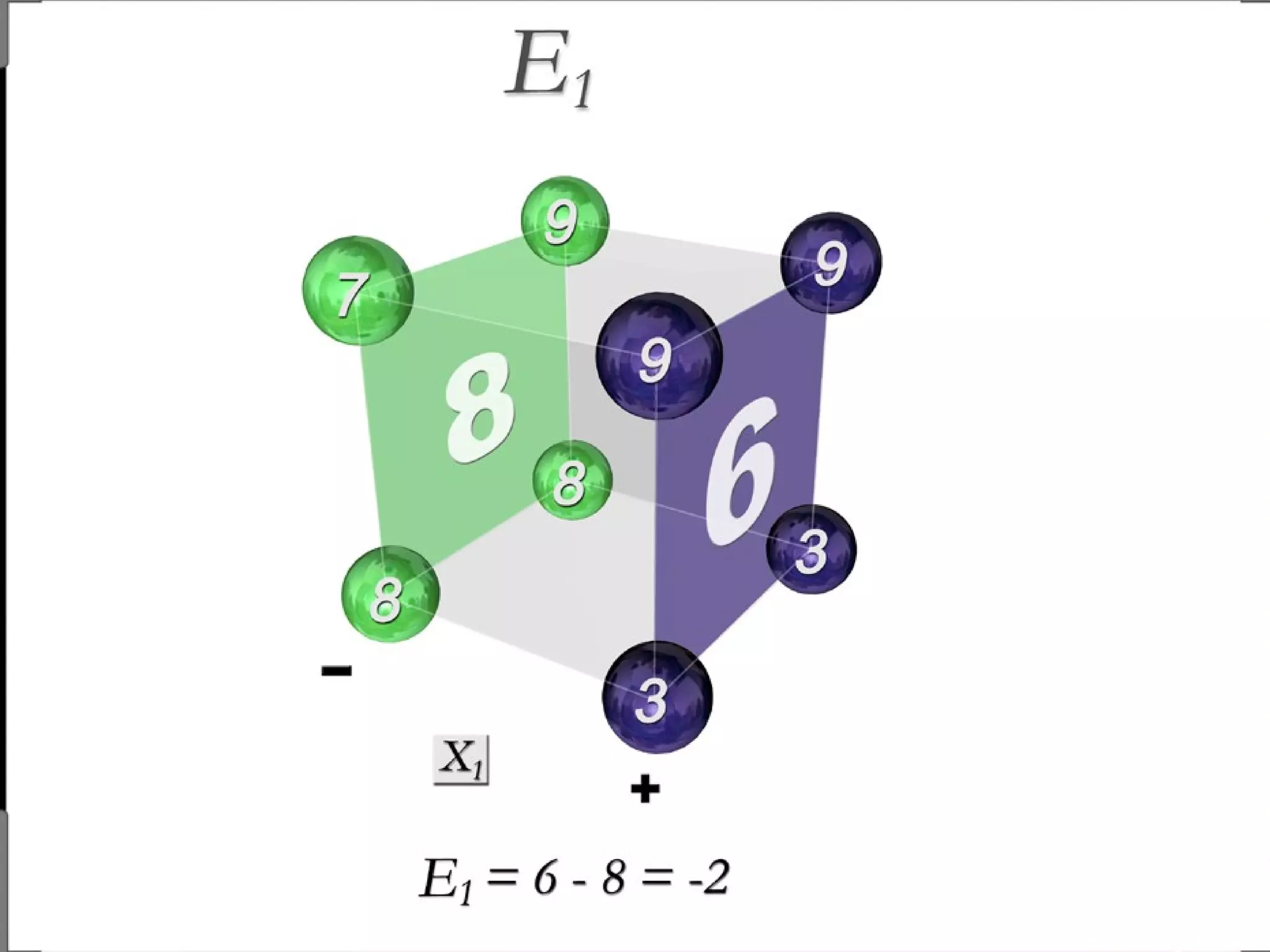
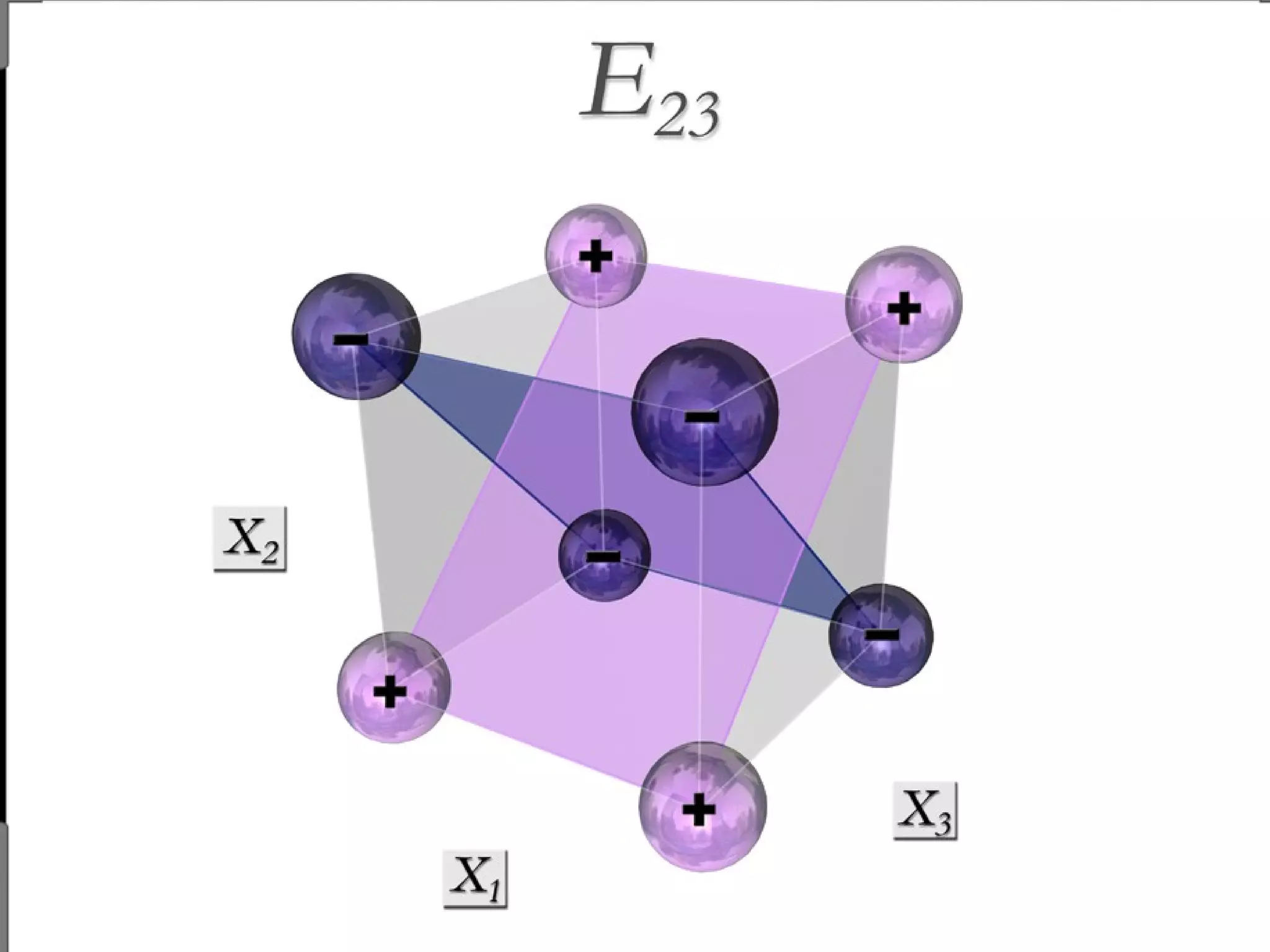
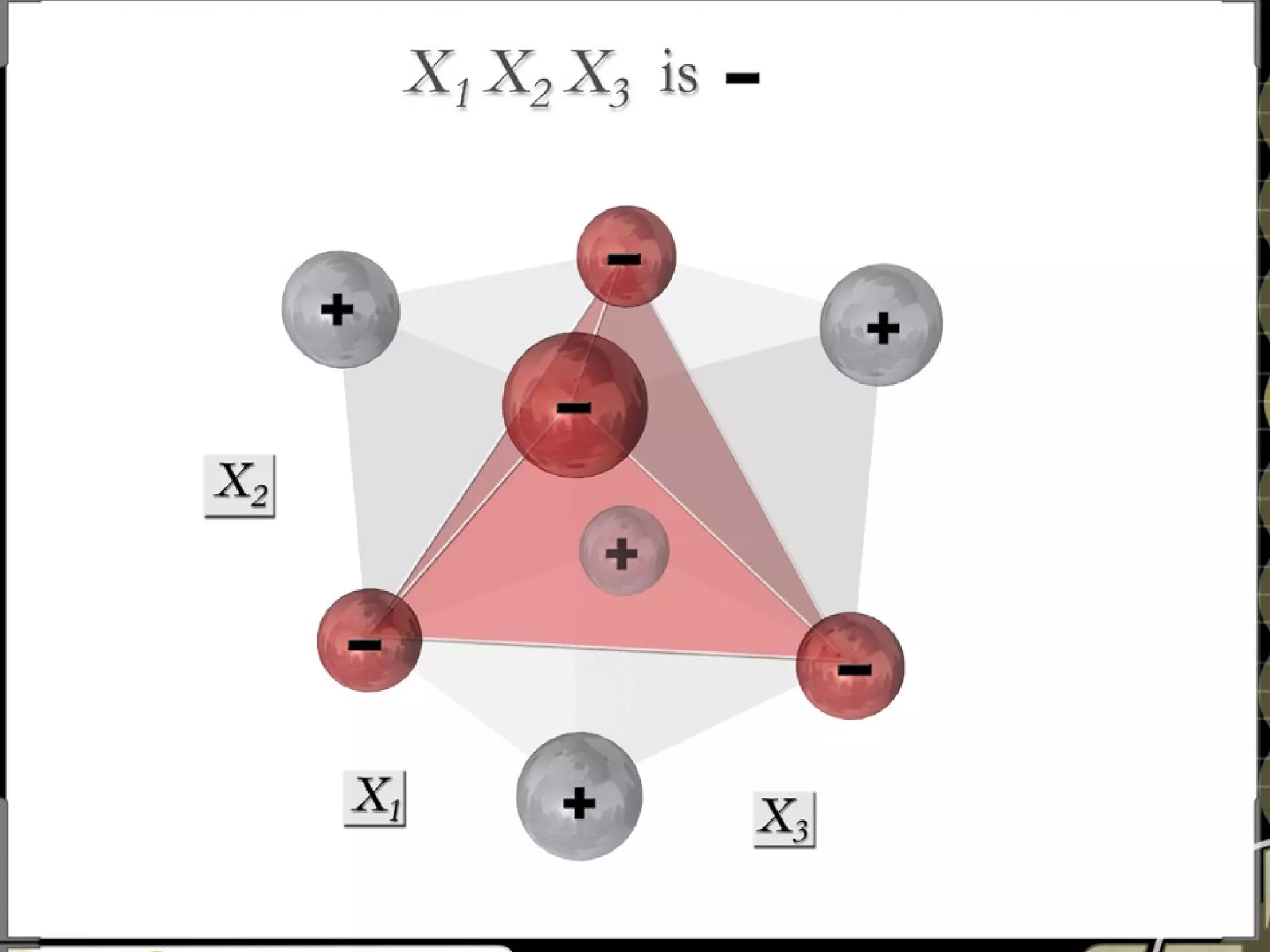
Fractional factorial designs (FFDs) are used to efficiently study many factors using fewer experimental runs than a full factorial design. FFDs exploit redundancy in estimating interactions to select a subset of runs. Regular FFDs have desirable properties like balance and orthogonality. Resolution indicates how interactions are aliased, with higher resolutions preferred. FFDs are useful in screening experiments to identify important factors efficiently before further optimization. Software helps select appropriate FFDs based on desired resolution and aliasing.
More Related Content
Similar to Fractional factorial design tutorial
Fractional factorial design tutorial
- 1. Fractional Factorial Designs: ATutorial Vijay Nair Departments of Statistics and Industrial & Operations Engineering vnn@umich.edu
- 2. Design of Experiments(DOE) in Manufacturing Industries • Statistical methodology for systematically investigating a system's input-output relationship to achieve one of several goals: – Identify important design variables (screening) – Optimize product or process design – Achieve robust performance • Key technology in product and process development Used extensively in manufacturing industries Part of basic training programs such as Six-sigma
- 3. Design and Analysisof Experiments A Historical Overview • Factorial and fractional factorial designs (1920+) Agriculture • Sequential designs (1940+) Defense • Response surface designs for process optimization (1950+) Chemical • Robust parameter design for variation reduction (1970+) Manufacturing and Quality Improvement • Virtual (computer) experiments using computational models (1990+) Automotive, Semiconductor, Aircraft, …
- 4. Overview • Factorial Experiments •Fractional Factorial Designs – What? – Why? – How? – Aliasing, Resolution, etc. – Properties – Software • Application to behavioral intervention research – FFDs for screening experiments – Multiphase optimization strategy (MOST)
- 5. (Full) Factorial Designs •All possible combinations • General: I x J x K … • Two-level designs: 2 x 2, 2 x 2 x 2, …
- 6. (Full) Factorial Designs •All possible combinations of the factor settings • Two-level designs: 2 x 2 x 2 … • General: I x J x K … combinations
- 7. Will focus on two-leveldesigns OK in screening phase i.e., identifying important factors
- 8. (Full) Factorial Designs •All possible combinations of the factor settings • Two-level designs: 2 x 2 x 2 … • General: I x J x K … combinations
- 9.
- 13.
- 15. Algebra -1 x -1= +1 …
- 17.
- 18. 9 + 9+ 3 + 3 6 7 + 9 + 8 + 8 8 6 – 8 = -2 7 9 9 9 8 3 8 3
- 24. Fractional Factorial Designs •Why? • What? • How? • Properties
- 25. Treatment combinations In engineering,this is the sample size -- no. of prototypes to be built. In prevention research, this is the no. of treatment combos (vs number of subjects) Why Fractional Factorials? Full Factorials No. of combinations This is only for two-levels
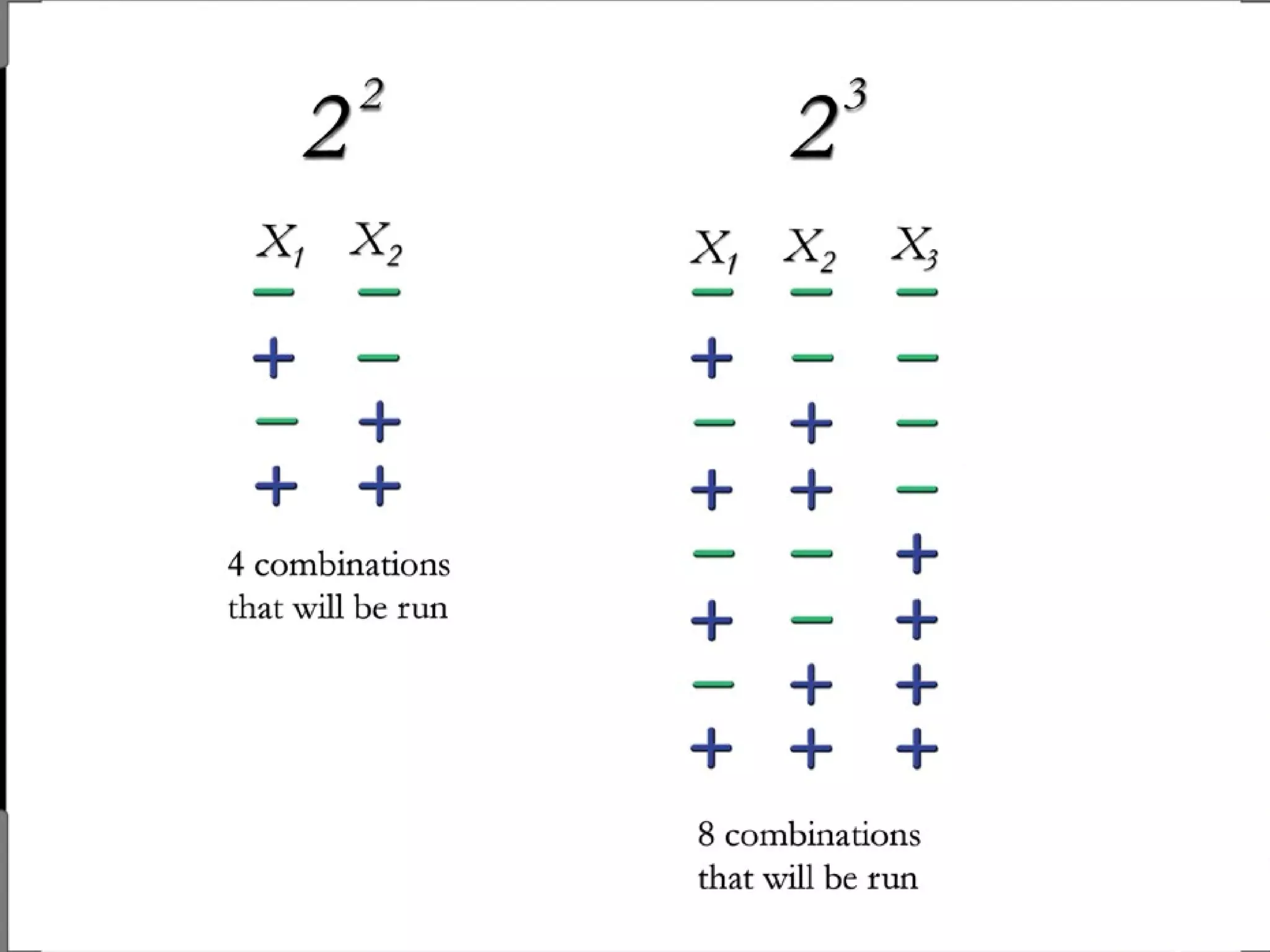
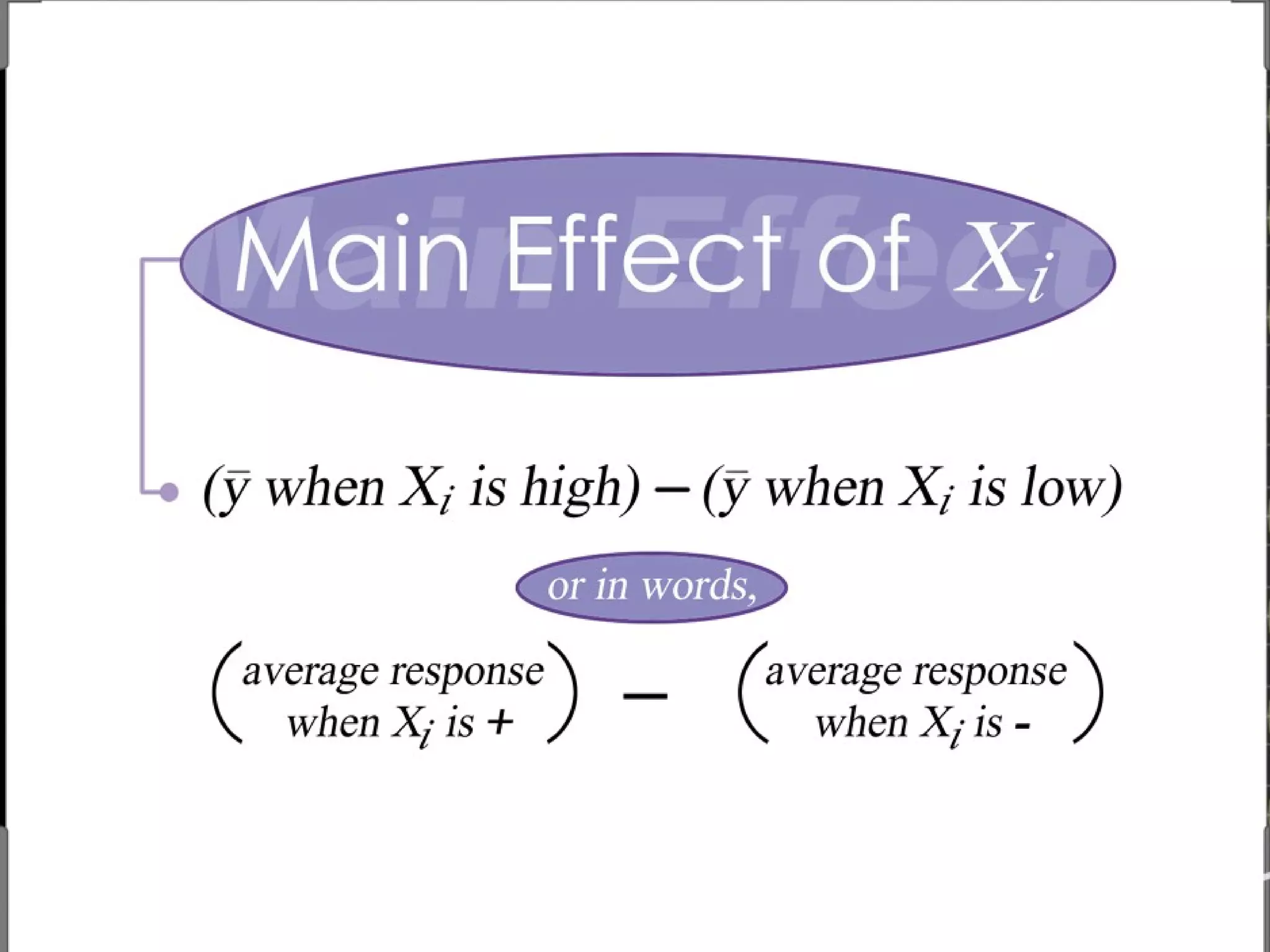
- 26. How? Box et al.(1978) “There tends to be a redundancy in [full factorial designs] – redundancy in terms of an excess number of interactions that can be estimated … Fractional factorial designs exploit this redundancy …” philosophy
- 27. How to selecta subset of 4 runs from a -run design? Many possible “fractional” designs
- 28.
- 29. Need a principledapproach! Here’s another …
- 30. Need a principledapproach for selecting FFD’s Regular Fractional Factorial Designs Wow! Balanced design All factors occur and low and high levels same number of times; Same for interactions. Columns are orthogonal. Projections … Good statistical properties
- 31. Need a principledapproach for selecting FFD’s What is the principled approach? Notion of exploiting redundancy in interactions Set X3 column equal to the X1X2 interaction column
- 32. Notion of “resolution” coming soon to theaters near you …
- 33. Need a principledapproach for selecting FFD’s Regular Fractional Factorial Designs Half fraction of a design = design 3 factors studied -- 1-half fraction 8/2 = 4 runs Resolution III (later)
- 34. X3 = X1X2 X1X3 = X2 and X2X3 = X1 (main effects aliased with two-factor interactions) – Resolution III design Confounding or Aliasing NO FREE LUNCH!!! X3=X1X2 ?? aliased
- 35. For half-fractions, alwaysbest to alias the new (additional) factor with the highest-order interaction term Want to study 5 factors (1,2,3,4,5) using a 2^4 = 16-run design i.e., construct half-fraction of a 2^5 design = 2^{5-1} design
- 37. X5 = X2*X3*X4;X6 = X1*X2*X3*X4; X5*X6 = X1 (can we do better?) What about bigger fractions? Studying 6 factors with 16 runs? ¼ fraction of
- 38. X5 = X1*X2*X3;X6 = X2*X3*X4 X5*X6 = X1*X4 (yes, better)
- 39. Design Generators and Resolution X5= X1*X2*X3; X6 = X2*X3*X4 X5*X6 = X1*X4 5 = 123; 6 = 234; 56 = 14 Generators: I = 1235 = 2346 = 1456 Resolution: Length of the shortest “word” in the generator set resolution IV here So …
- 40. Resolution Resolution III: (1+2) Maineffect aliased with 2-order interactions Resolution IV: (1+3 or 2+2) Main effect aliased with 3-order interactions and 2-factor interactions aliased with other 2-factor … Resolution V: (1+4 or 2+3) Main effect aliased with 4-order interactions and 2-factor interactions aliased with 3-factor interactions
- 41. X5 = X2*X3*X4;X6 = X1*X2*X3*X4; X5*X6 = X1 or I = 2345 = 12346 = 156 Resolution III design ¼ fraction of
- 42. X5 = X1*X2*X3;X6 = X2*X3*X4 X5*X6 = X1*X4 or I = 1235 = 2346 = 1456 Resolution IV design
- 43. Aliasing Relationships I =1235 = 2346 = 1456 Main-effects: 1=235=456=2346; 2=135=346=1456; 3=125=246=1456; 4=… 15-possible 2-factor interactions: 12=35 13=25 14=56 15=23=46 16=45 24=36 26=34
- 44. Balanced designs Factors occurequal number of times at low and high levels; interactions … sample size for main effect = ½ of total. sample size for 2-factor interactions = ¼ of total. Columns are orthogonal … Properties of FFDs
- 45. How to chooseappropriate design? Software for a given set of generators, will give design, resolution, and aliasing relationships SAS, JMP, Minitab, … Resolution III designs easy to construct but main effects are aliased with 2-factor interactions Resolution V designs also easy but not as economical (for example, 6 factors need 32 runs) Resolution IV designs most useful but some two-factor interactions are aliased with others.
- 46. Selecting Resolution IVdesigns Consider an example with 6 factors in 16 runs (or 1/4 fraction) Suppose 12, 13, and 14 are important and factors 5 and 6 have no interactions with any others Set 12=35, 13=25, 14= 56 (for example) I = 1235 = 2346 = 1456 Resolution IV design All possible 2-factor interactions: 12=35 13=25 14=56 15=23=46 16=45 24=36 26=34
- 47. PATTERN OE-DEPTH DOSETESTIMO NIALS FRAMING EE-DEPTH SOURCE SOURCE- DEPTH +----+- LO 1 HI Gain HI Team HI --+-++- HI 1 LO Gain LO Team HI ++----+ LO 5 HI Gain HI HMO LO +---+++ LO 1 HI Gain LO Team LO ++-++-+ LO 5 HI Loss LO HMO LO --+--++ HI 1 LO Gain HI Team LO +--+++- LO 1 HI Loss LO Team HI -++---- HI 5 LO Gain HI HMO HI -++-+-+ HI 5 LO Gain LO HMO LO -++++-- HI 5 LO Loss LO HMO HI ----+-- HI 1 HI Gain LO HMO HI -+-+++- HI 5 HI Loss LO Team HI Factors Source Source-Depth OE-Depth X X Dose X X Testimonials X Framing X EE-Depth X Effects Aliases OE-Depth*Dose = Testimonials*Source OEDepth*Testimonials = Dose*Source OE-Depth*Source = Dose*Testimonials Project 1: 2^(7-2) design 32 trx combos
- 48. Role of FFDsin Prevention Research • Traditional approach: randomized clinical trials of control vs proposed program • Need to go beyond answering if a program is effective inform theory and design of prevention programs “opening the black box” … • A multiphase optimization strategy (MOST) center projects (see also Collins, Murphy, Nair, and Strecher) • Phases: – Screening (FFDs) – relies critically on subject-matter knowledge – Refinement – Confirmation