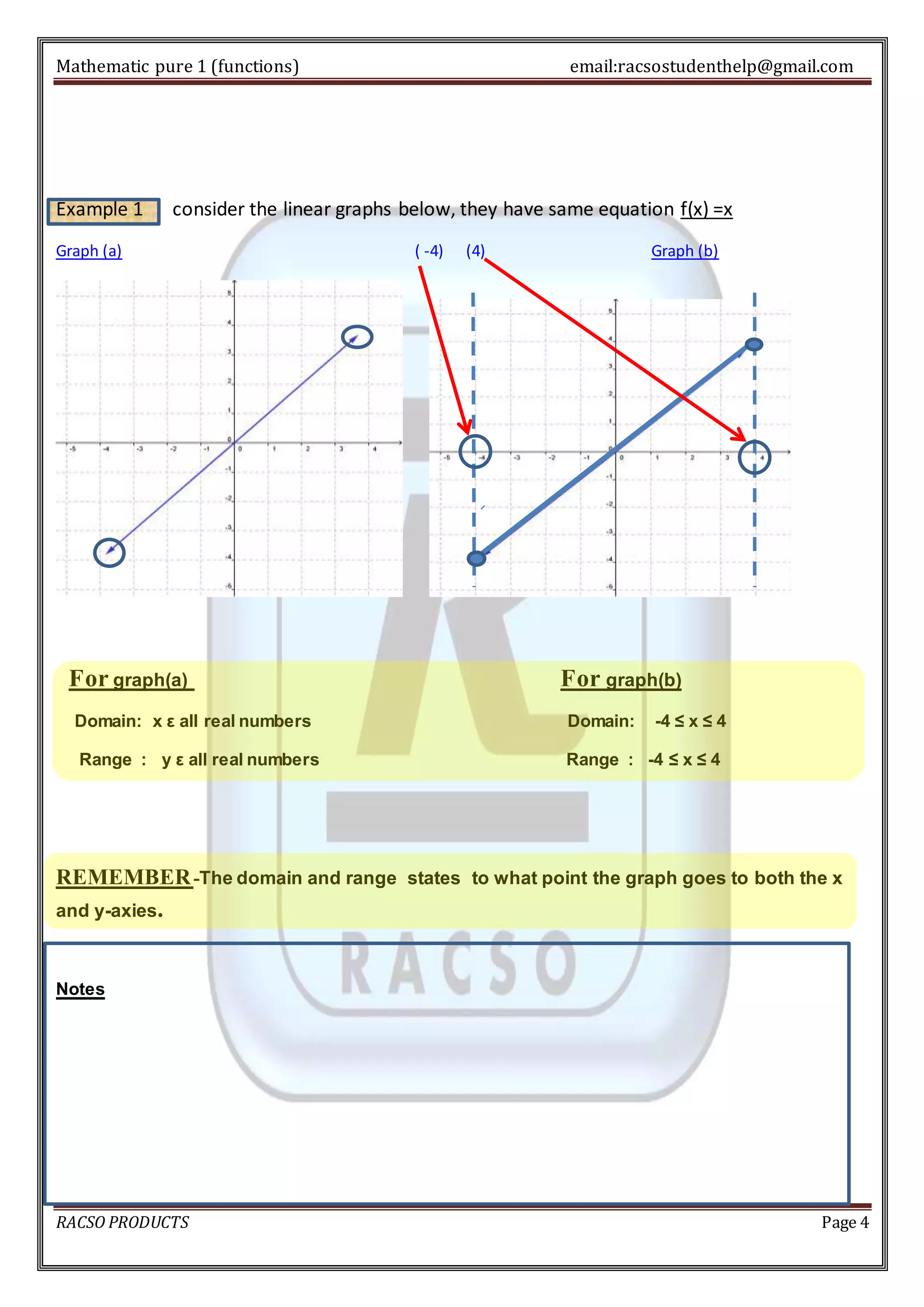
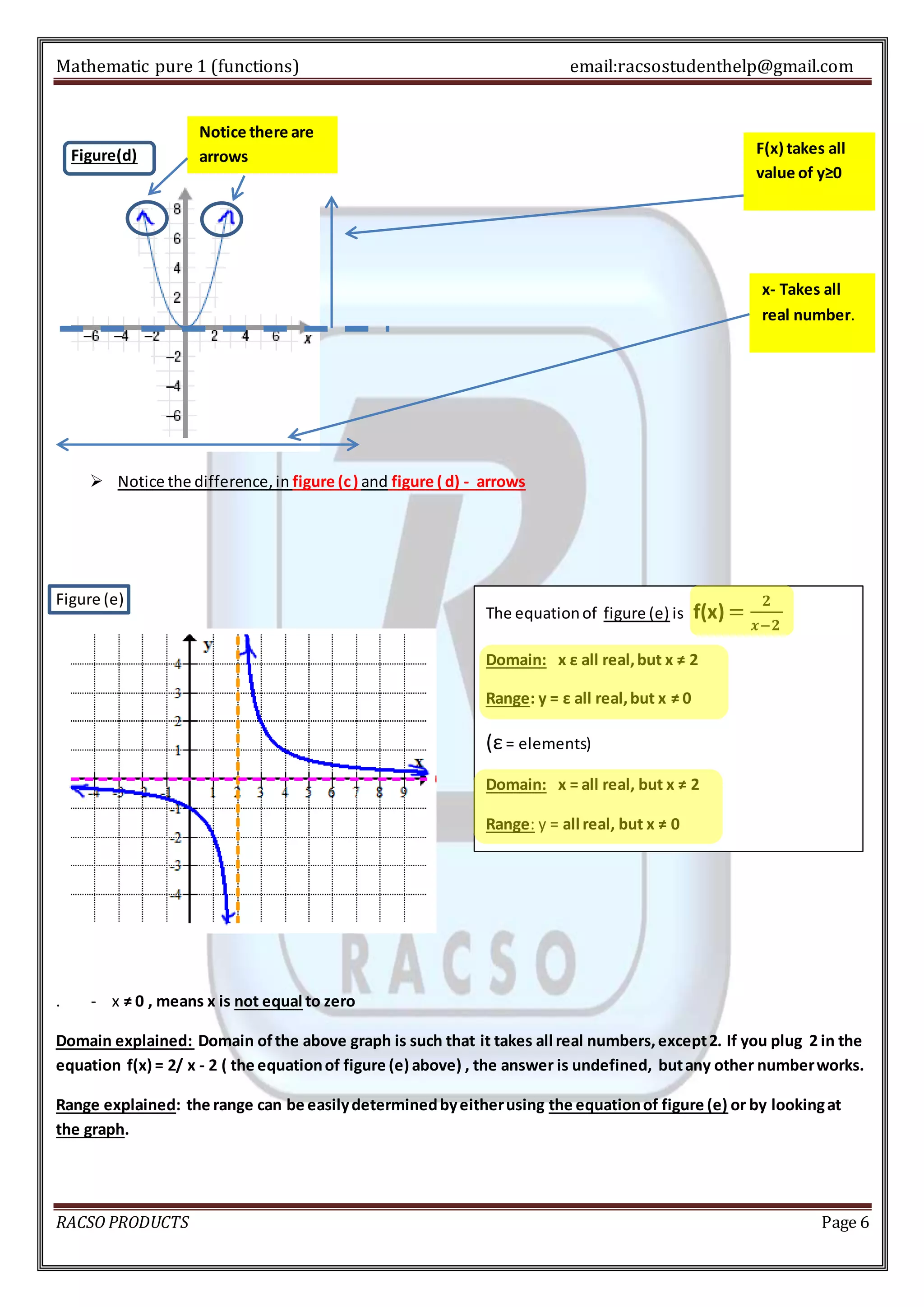
1. A function is a relationship between inputs and outputs where each input corresponds to exactly one output. The domain of a function is the set of possible inputs, and the range is the set of possible outputs.
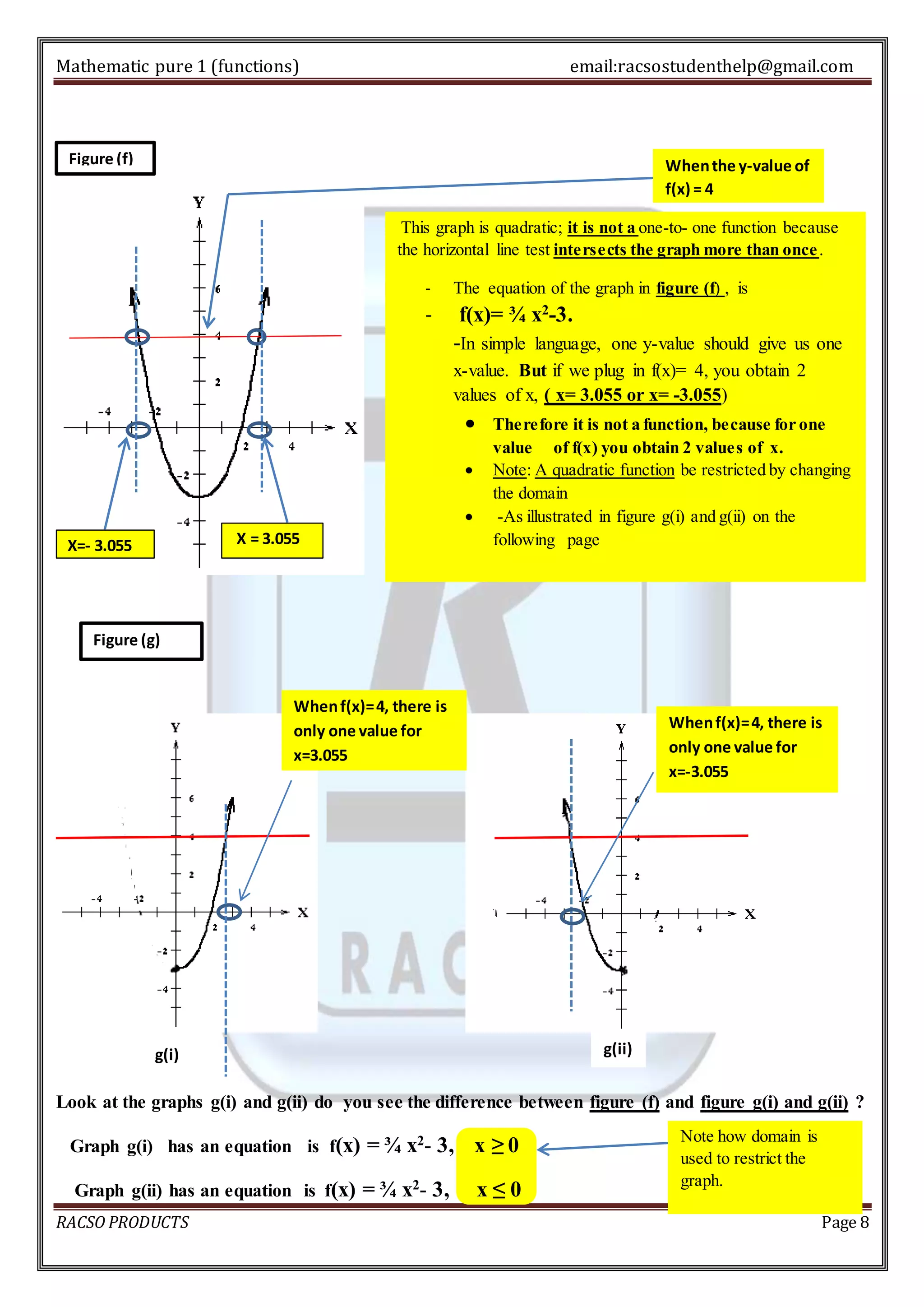
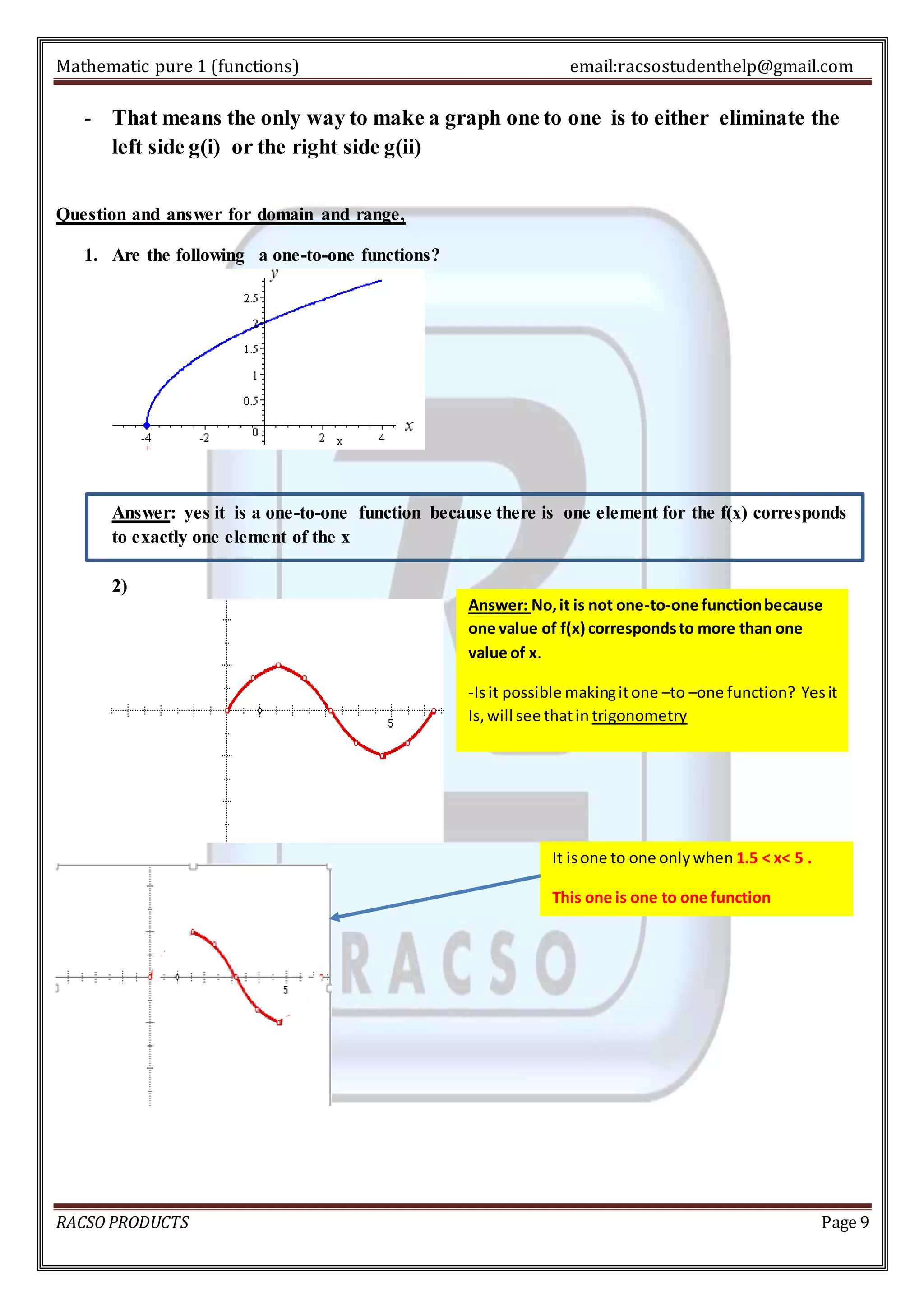
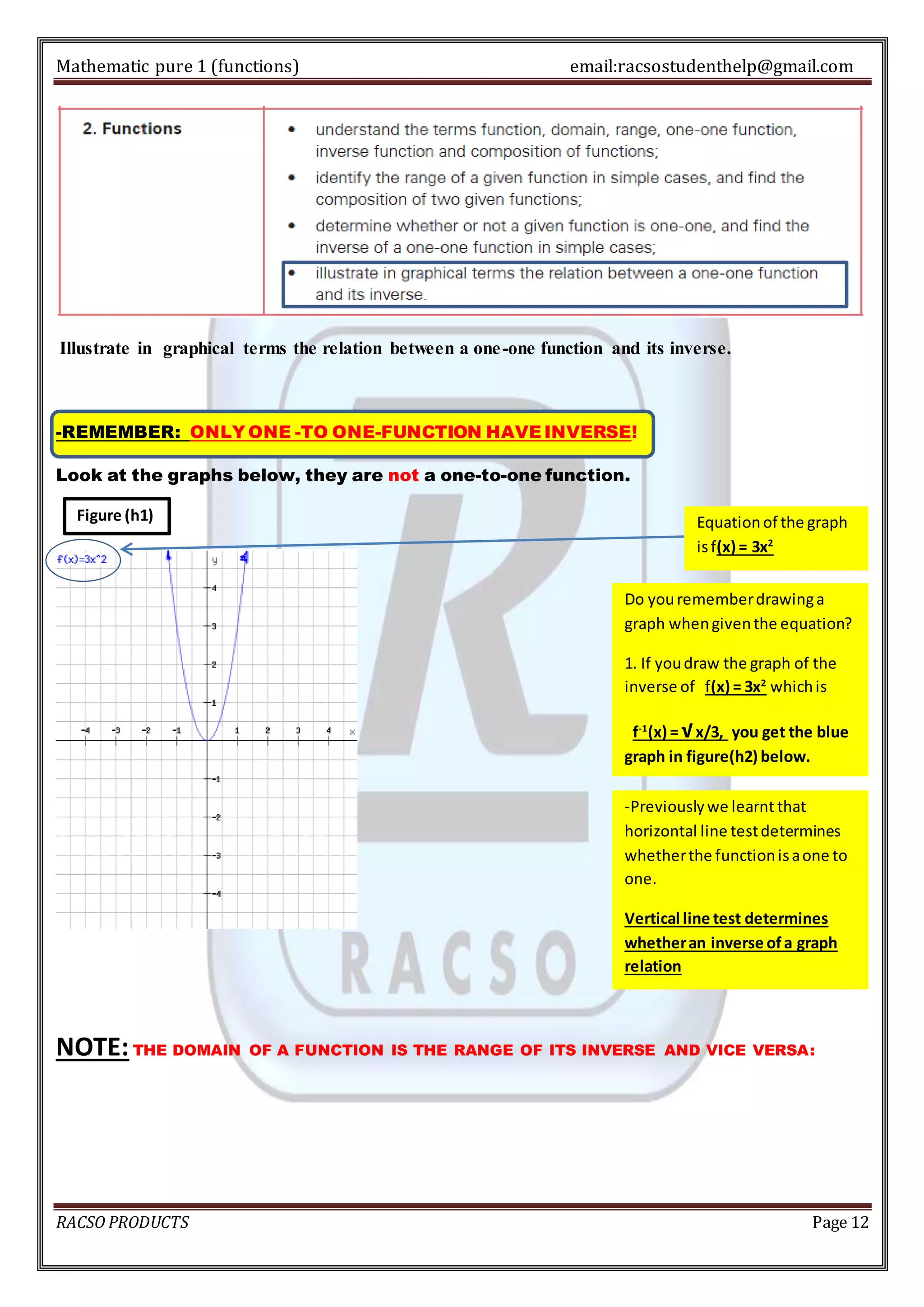
2. For a function to be one-to-one, each output must correspond to only one input. This can be tested using the horizontal line test - drawing horizontal lines on the graph. Restricting the domain can make non-one-to-one functions one-to-one.
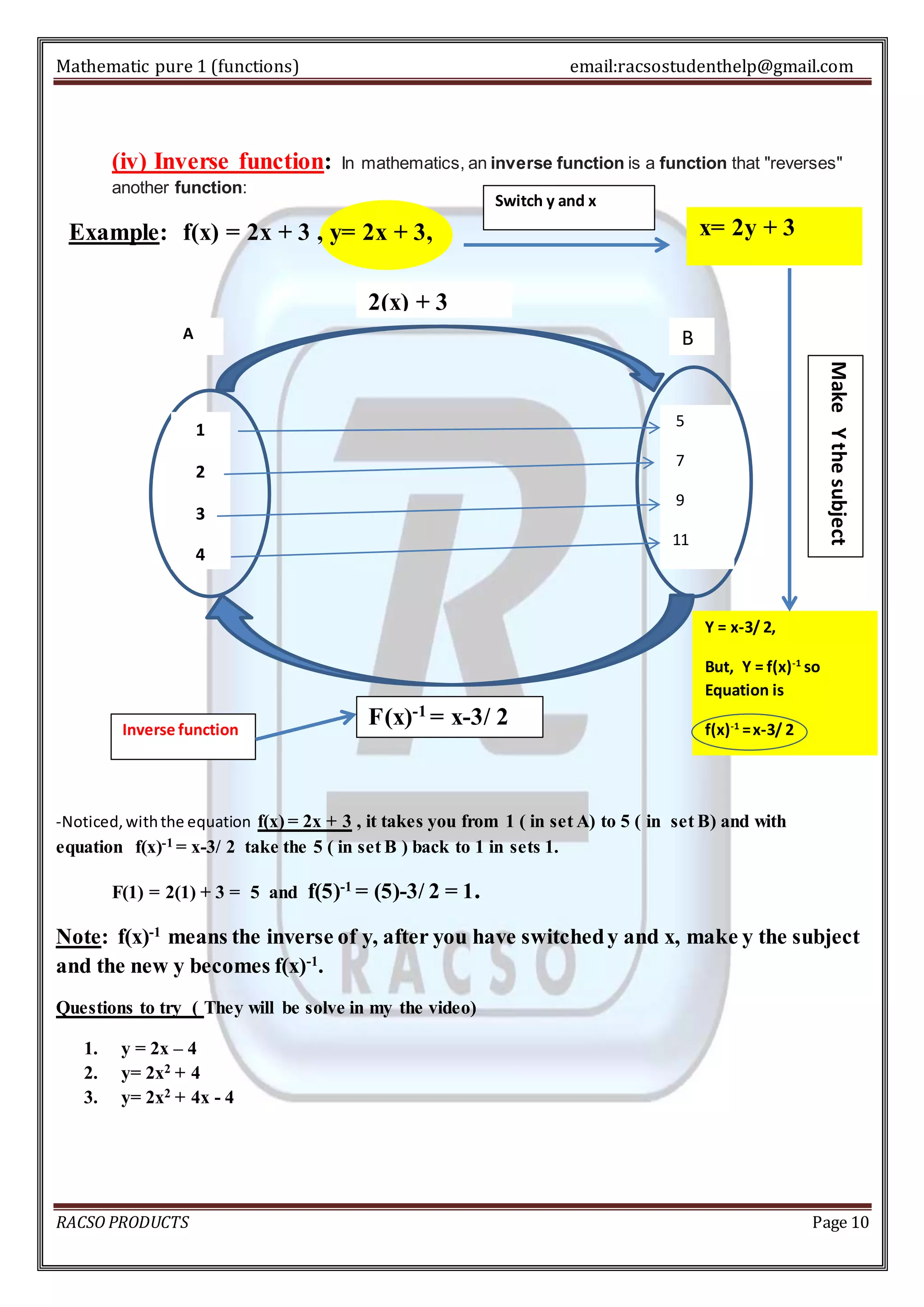
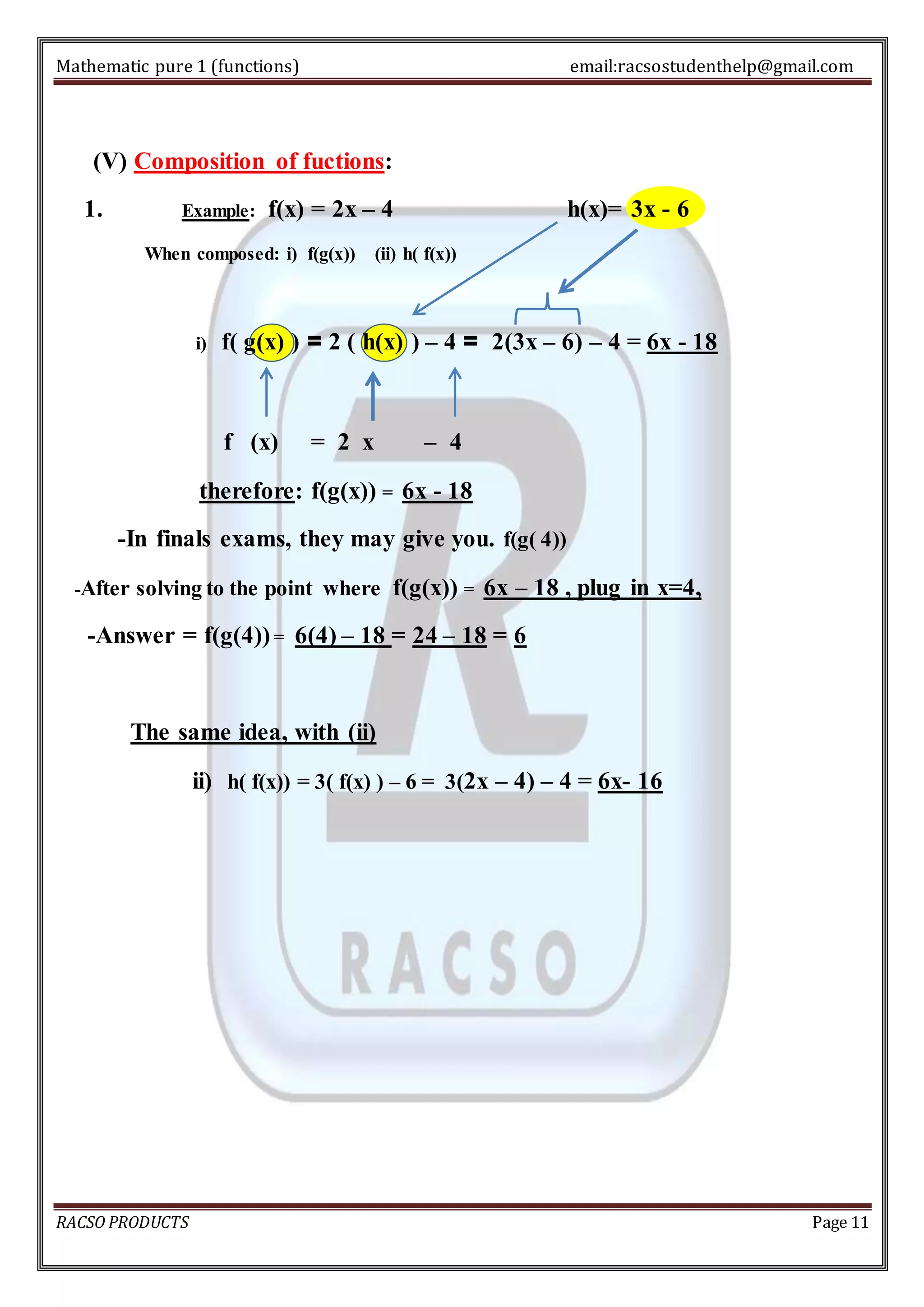
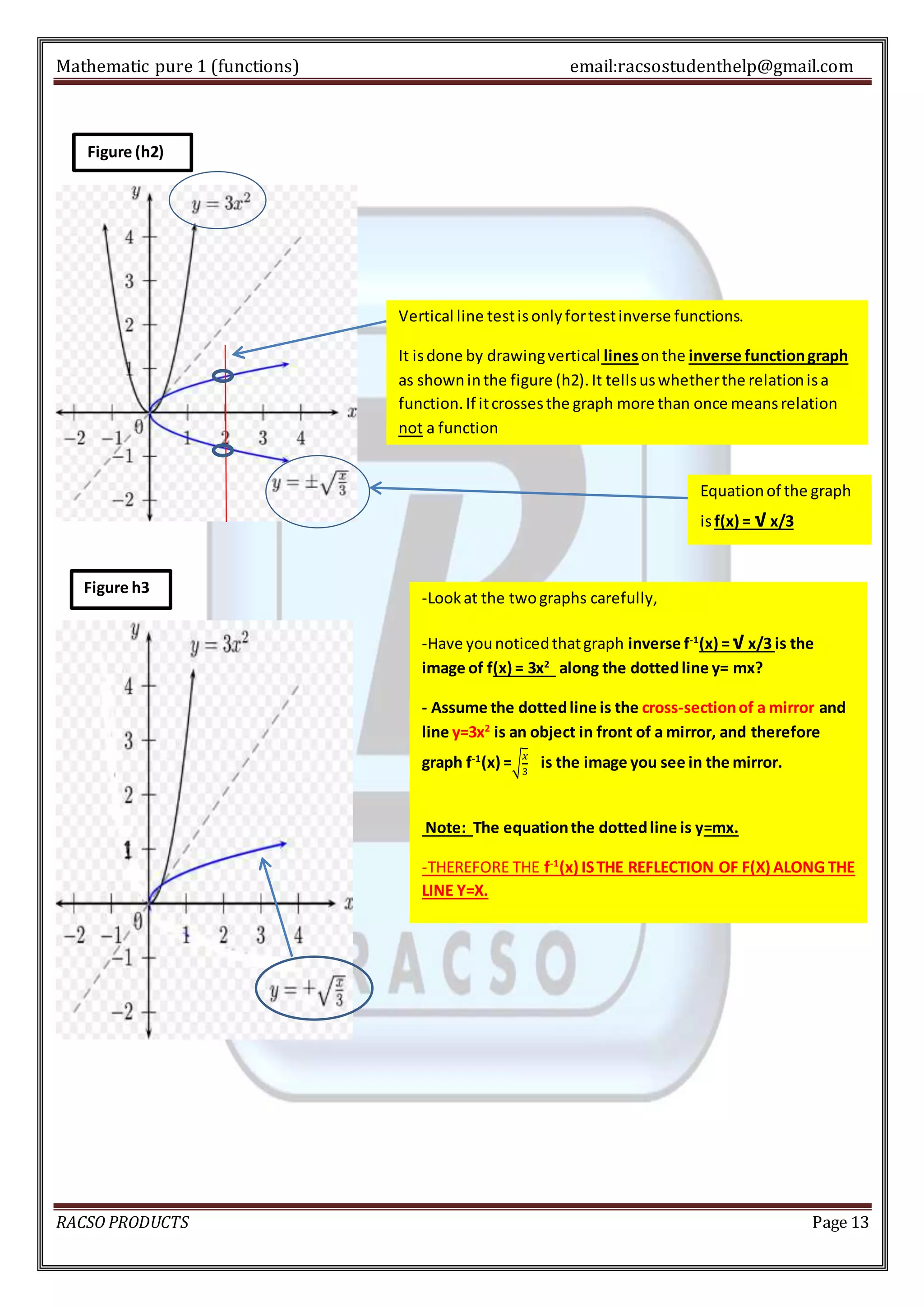
3. The inverse of a function undoes the input-output relationship by switching the domain and range. Only one-to-one functions have inverses. The graph of an inverse function passes the vertical