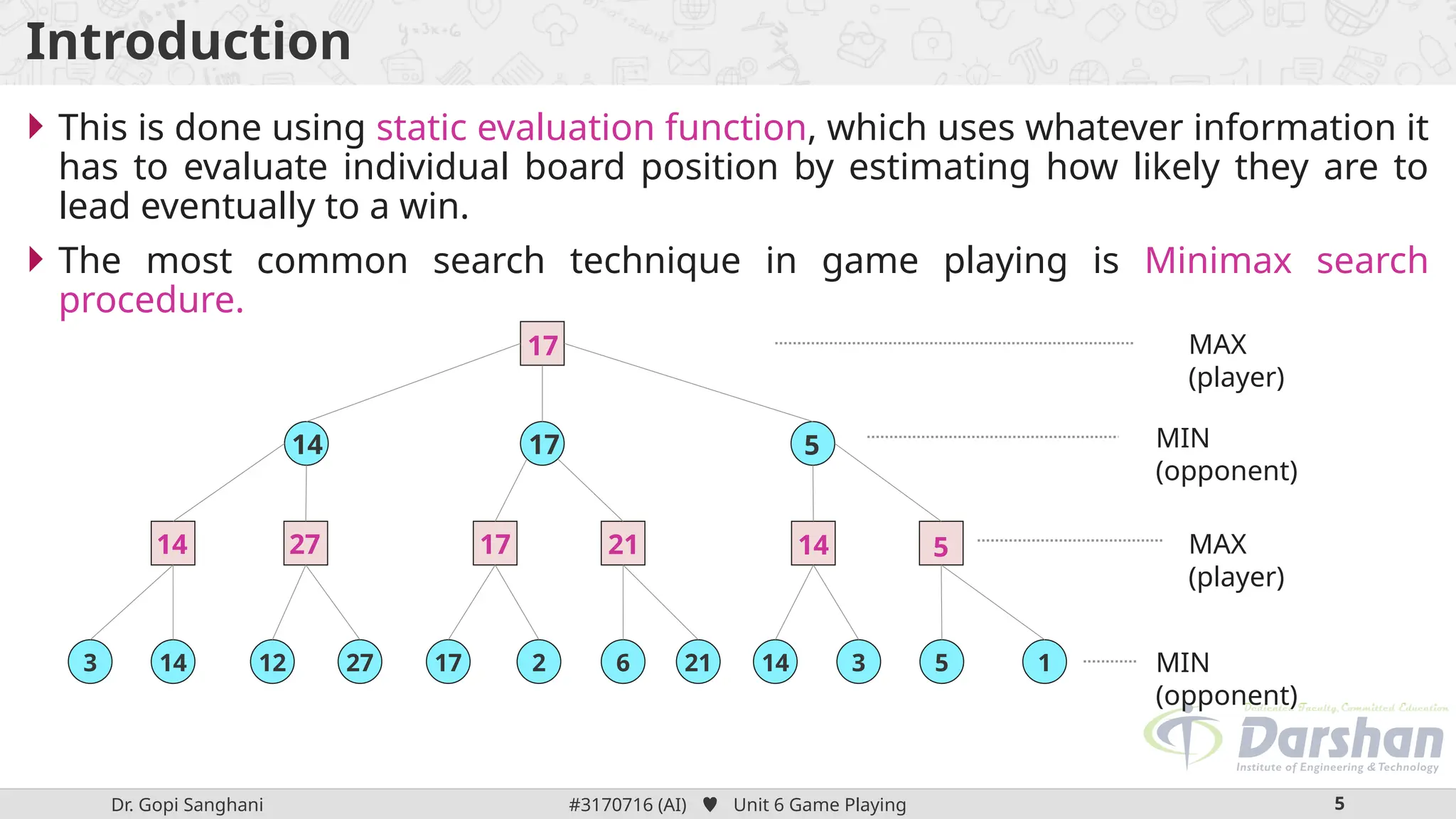
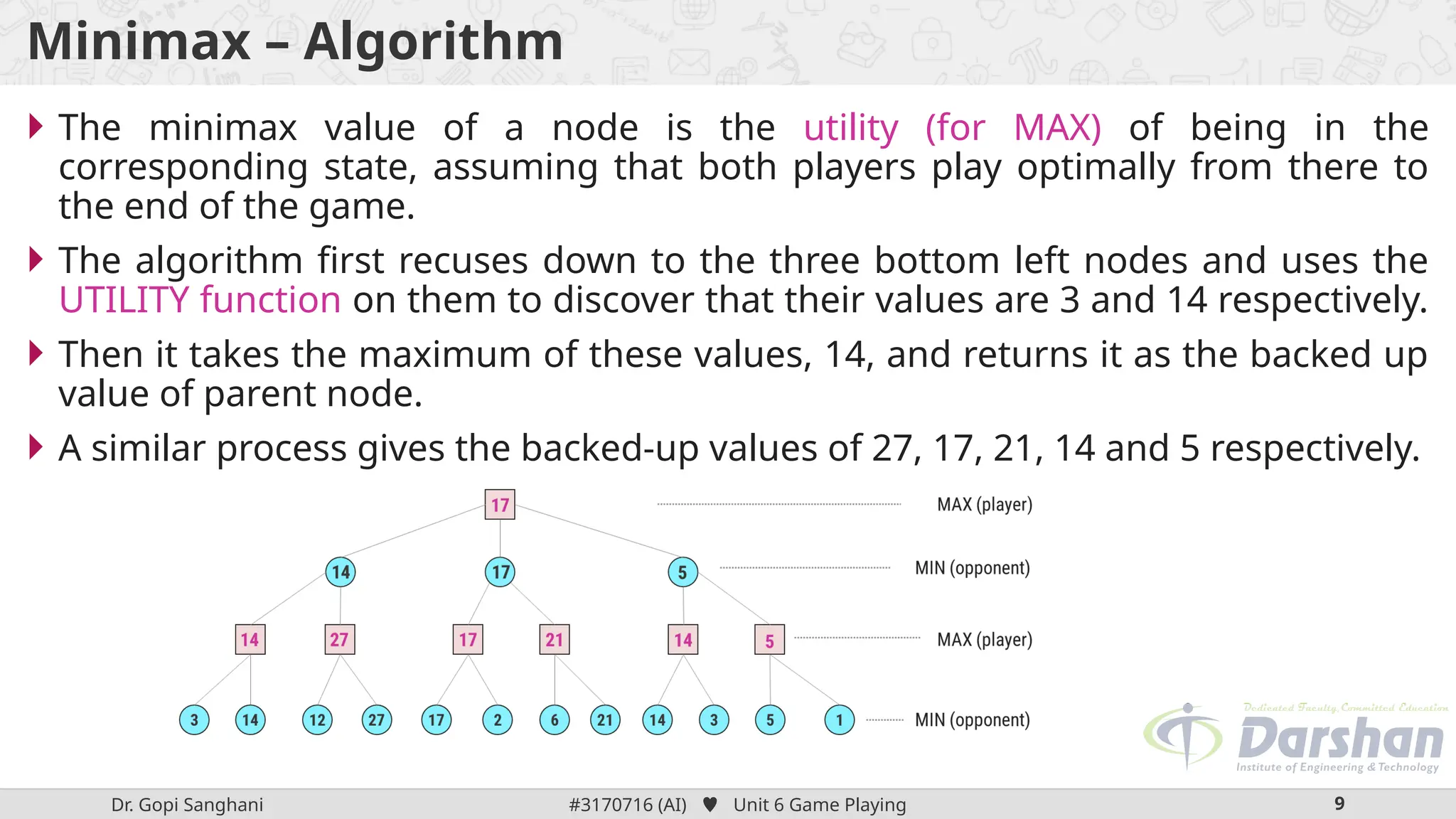
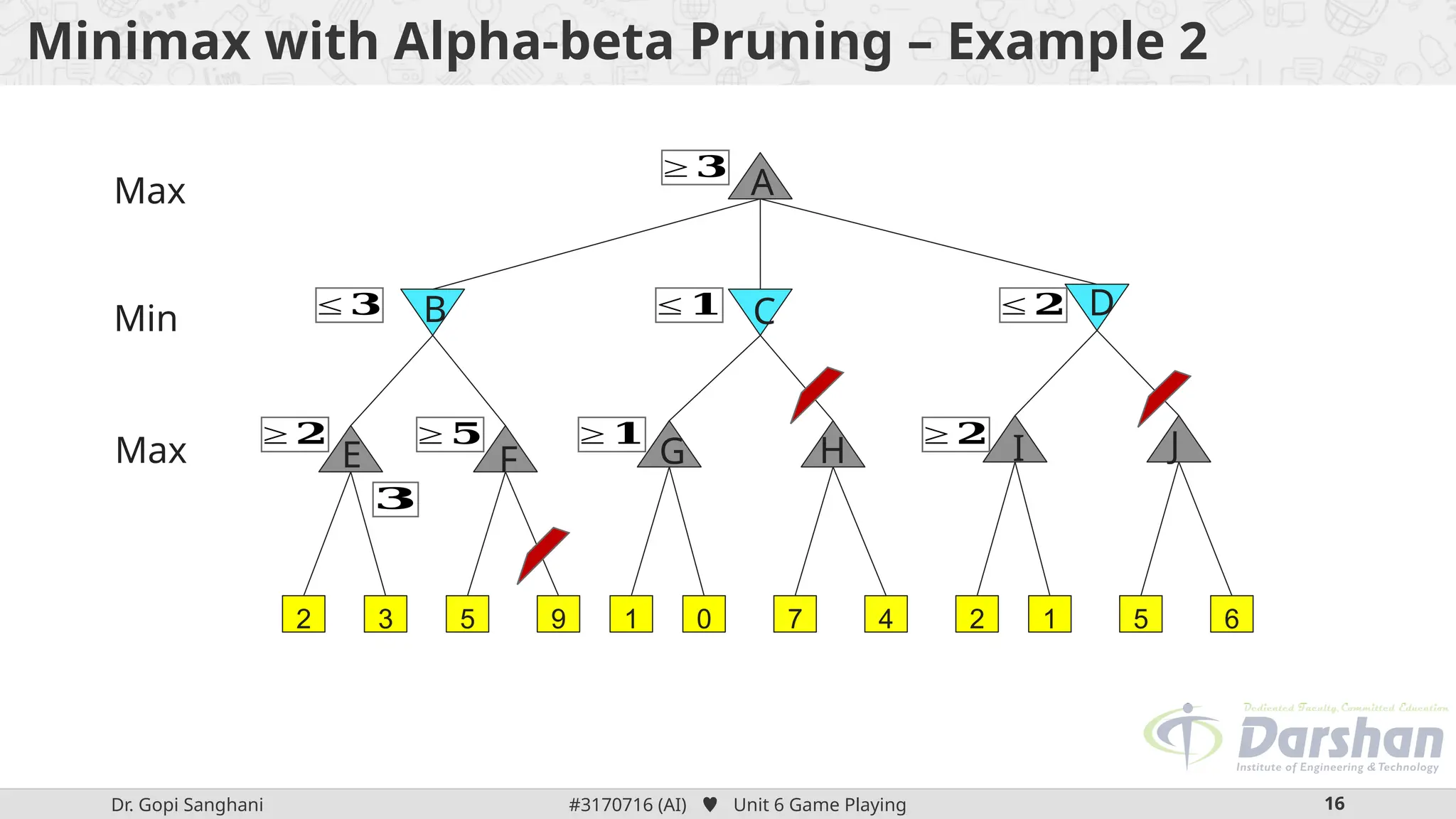
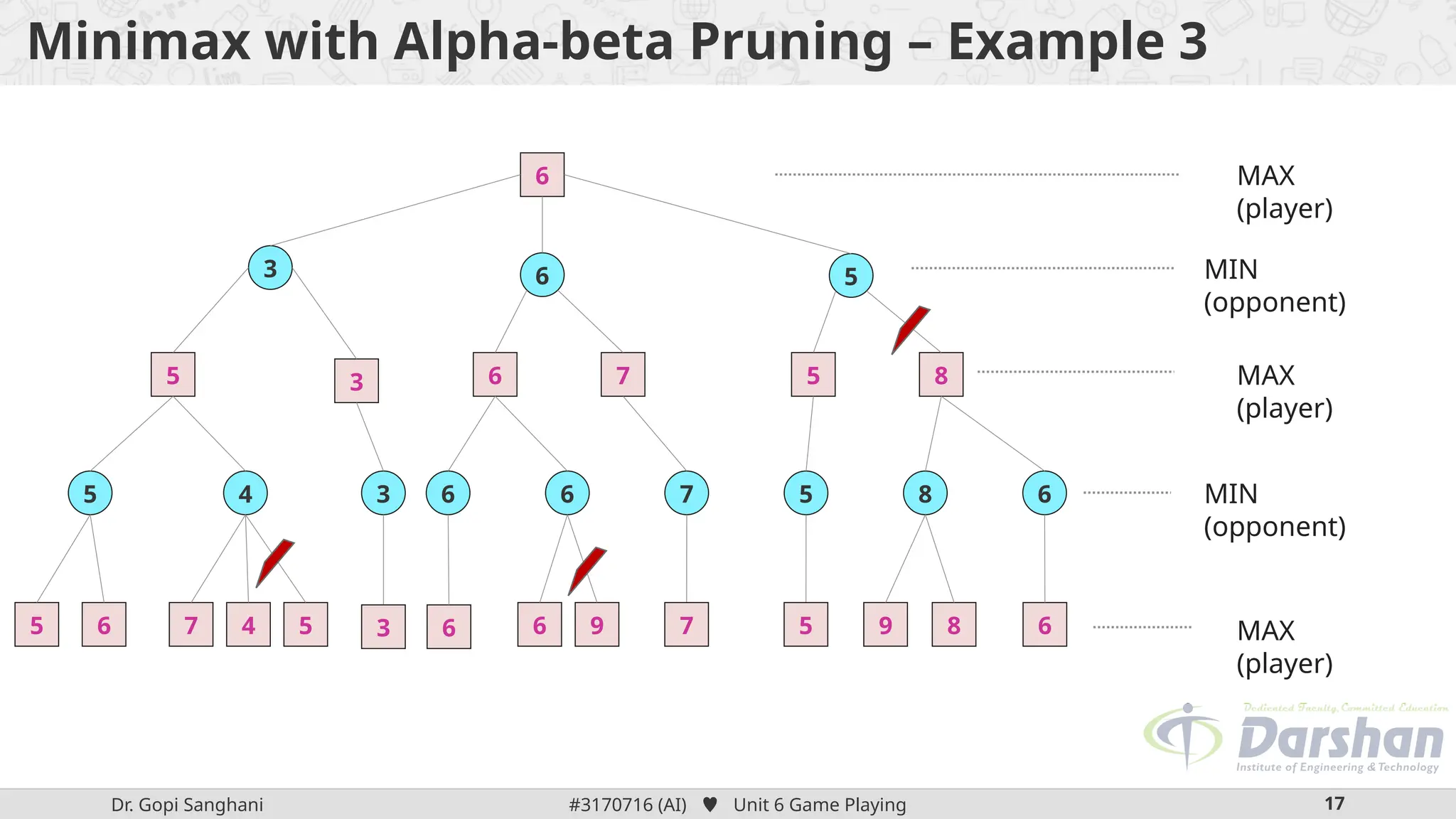
This document discusses the role of game playing in artificial intelligence, emphasizing the structured nature of games for measuring success and the techniques for improving search algorithms, notably the minimax search procedure with alpha-beta pruning. It explains the mechanics of minimax, including the recursive evaluation of game states, and introduces game refinement theory, which evaluates the sophistication and attractiveness of games. Overall, it highlights the importance of heuristic approaches to enhance performance in AI-driven game playing.